基于python实现的paillier算法例子（极简）

参考：经典同态加密算法Paillier解读 - 原理、实现和应用

    文中对Pailler进行了详细的解读并分享了相关源代码链接：python-phe同台算法库

    举了一个简单的例子：

2.3 Paillier算法

这里代码中lam = λ mu=μ，由以上计算过程获得

Alice将 n 和g 封装成公钥 public-key = (n, g)
将λ和μ封装成私钥: private-key = (λ, μ)

执行前我们需要安装gmpy2库

！pip install gmpy2

加密：

Bob需要对明文进行加密，即获取了Alice发来的公钥public-key = (n, g)

import gmpy2

p = 11 #大素数
q = 19 #大素数
n = 209 #乘积
lam = 90 #最小公倍数
g = 147 #随机整数
mu = 153 

#明文m 以及 随机数r已经定义
m = 8
r = 3
n_square = pow(n, 2) # n_square = 43681
c = gmpy2.mod(pow(g, m)*pow(r, n), n_square) # c =  32948
print(c)
#输出结果 32948 即加密结果

解密

c = 32948
m  = gmpy2.mod(L(gmpy2.mod(pow(c, lam), n_square), n) * mu, n) # m = 8

在这里，代码中有一个L函数，原文并没有写出来。

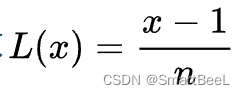
此函数在计算μ时实际上会用到，但原文没有进行函数计算，而是直接得出了μ的值。

然而，解密时仍然需要用到，下面附上。

函数L代码实现非常简单：

def L(x,n):
    return (x - 1) / n

至此，简单的Paillier算法示例结束。