0
0

MFC计算器——万字长文/一看就懂（需要的建议点赞收藏）

一、创建VS文件

首先，打开vs，选择如图所示左边的MFC应用。更改项目名称并选择自己想存入的位置后，点击创建。

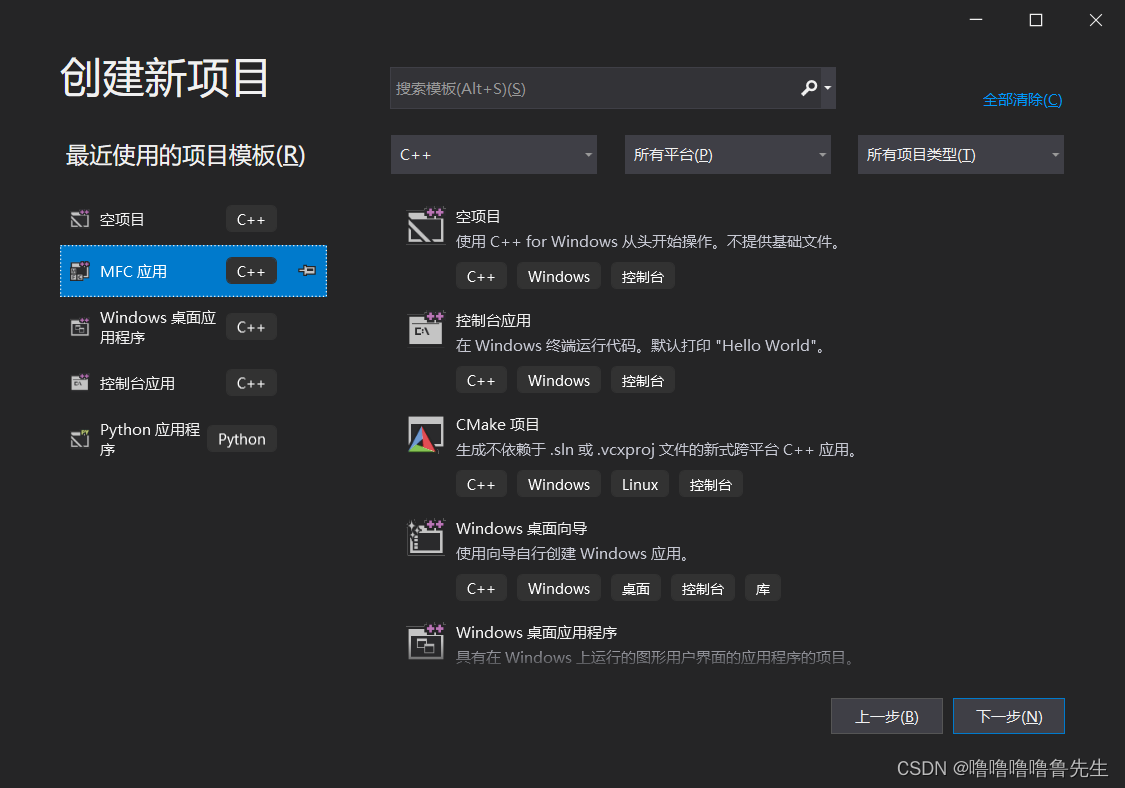
点击创建后，在应用程序类型中选择“基于对话框”，如下图。

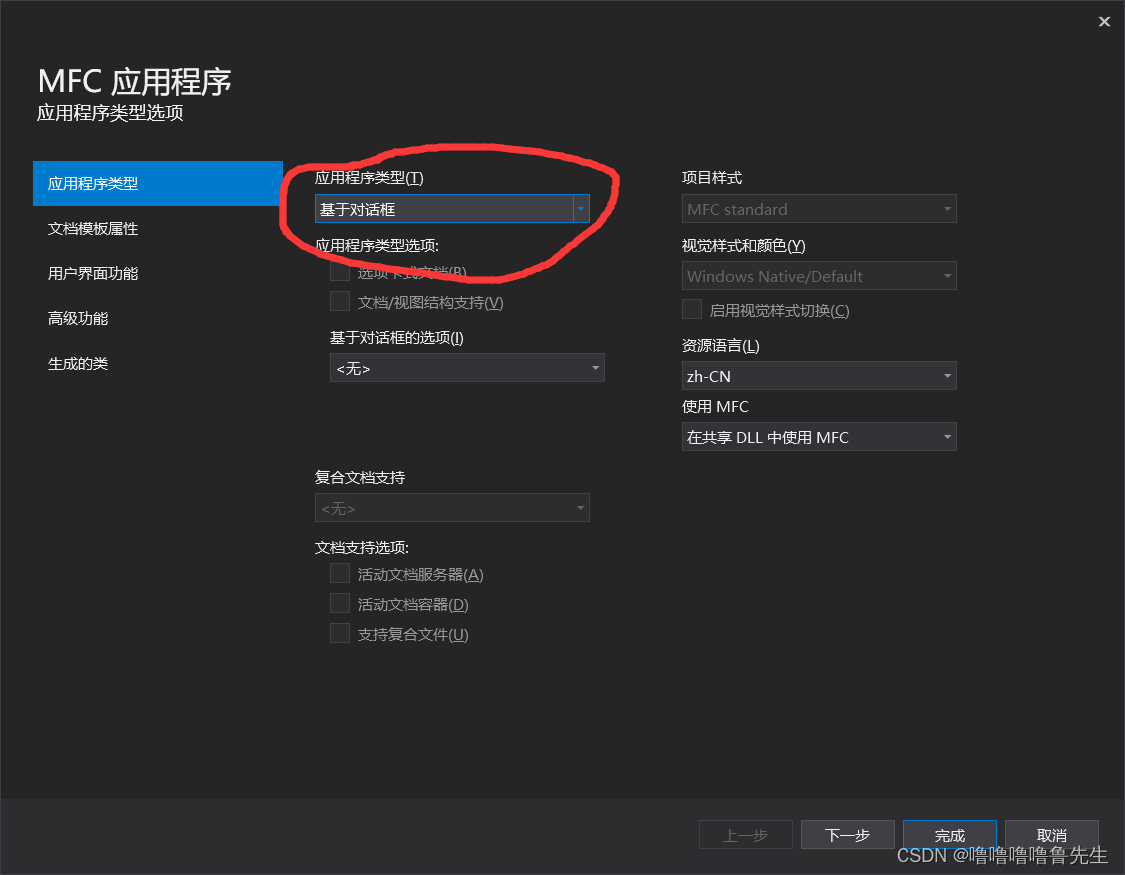
其他名称无需更改。可以在生成的类中更改类名，如下图，我改为MFC_Calculator。

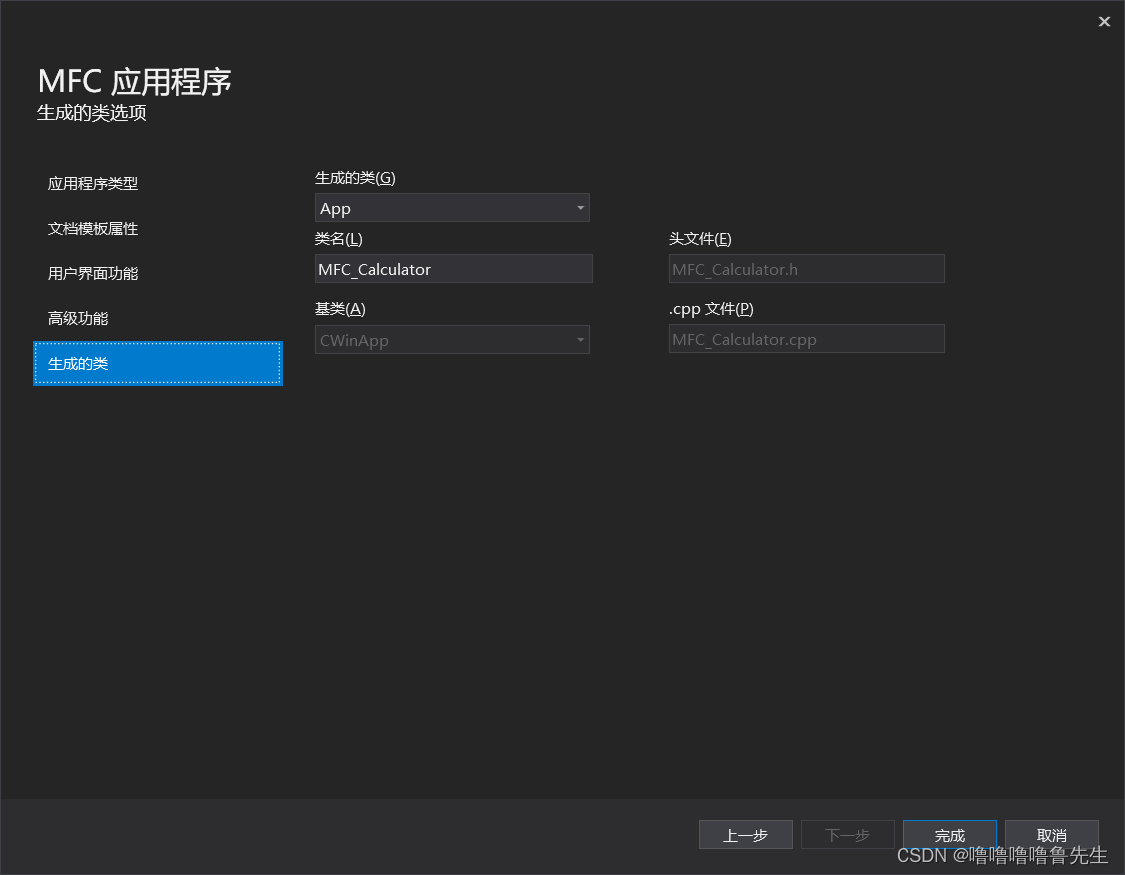
点击完成后来到这个界面。屏幕左侧有“工具箱”。工具箱里面有我们会用到的一些组件。

二、对于计算器界面的创建

我的MFC计算器界面如下，这个也是这篇文章的最终目标。

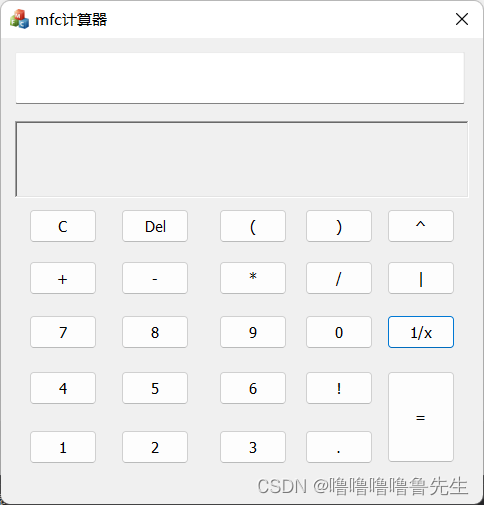
可以看出，这个计算器具有整数和小数的加、减、乘、除等基本运算，也有倒数、次方、阶乘运算，以及有括号的复合运算，并具有清零（C），删除（Del）等功能。

接下来我们来一一创建。

1.添加Edit Control

在左侧的工具箱找到Edit Control组件，点击添加至我们的界面。

添加后，调整合适的大小。界面右下角的确定、取消按钮，可以单击右键，选择删除。调整完成后，如图

2.添加Static Text

左侧工具箱中选择Static Text，添加至界面，并调整位置和大小。

此时，右键单击刚添加的Static Text，选择最下方的属性，将边框更改为True。如下图。

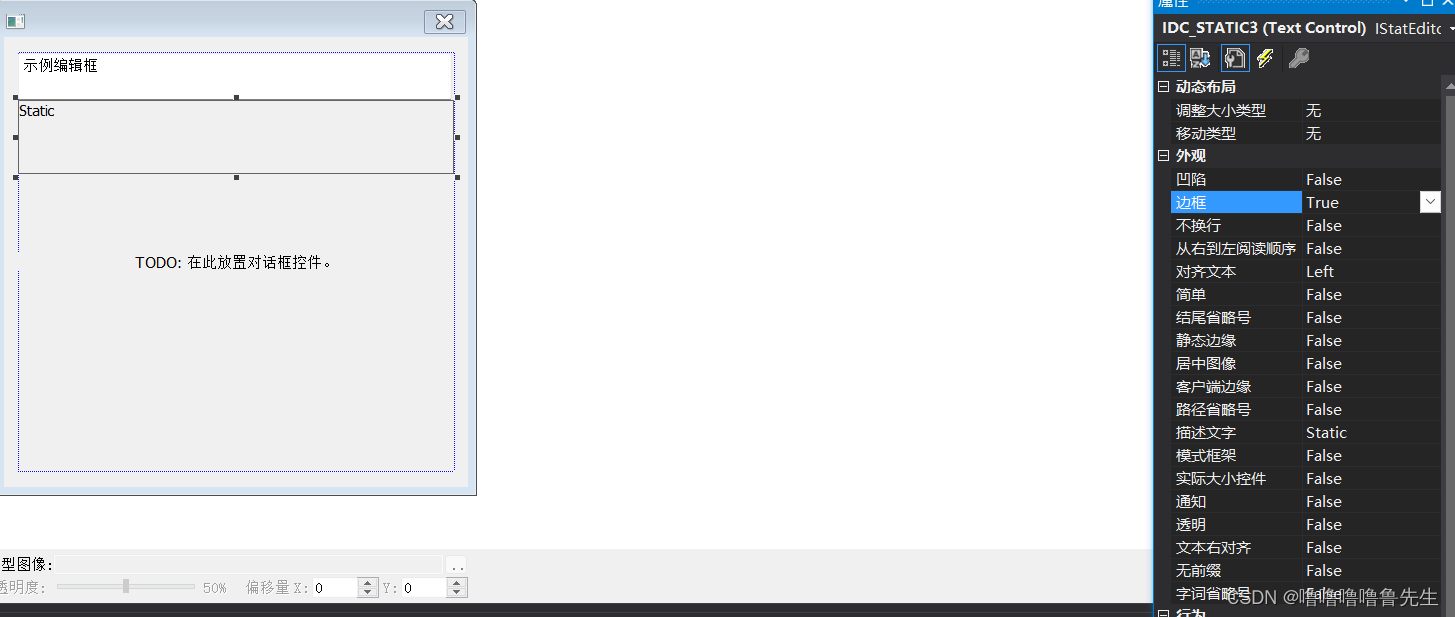
3.添加Button

将界面中间的“TODO：在此放置对话框控件。”右键单击删除。

左侧工具箱中选择Button，添加至界面。共添加24个Button。可以利用复制粘贴的方式快速添加。

添加后可以在VS的工具栏中找到对齐方式快速对齐

然后一一更改每个Button的属性中的描述文字和ID

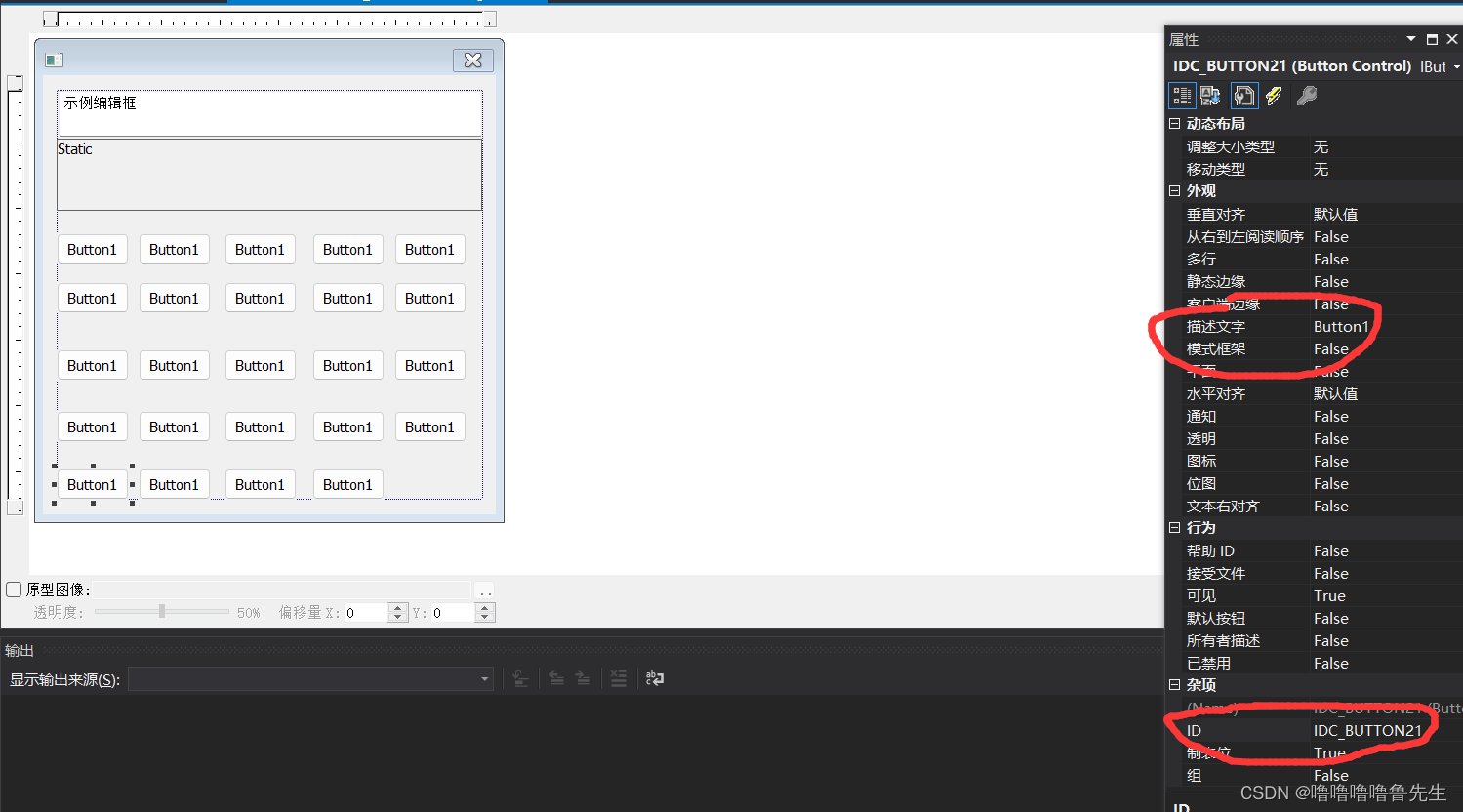
数字1 位于界面左下方，所以左下方的Button的描述文字改为“1”，ID我改为“IDC_BUTTON_1”。

更改完成后如下图。

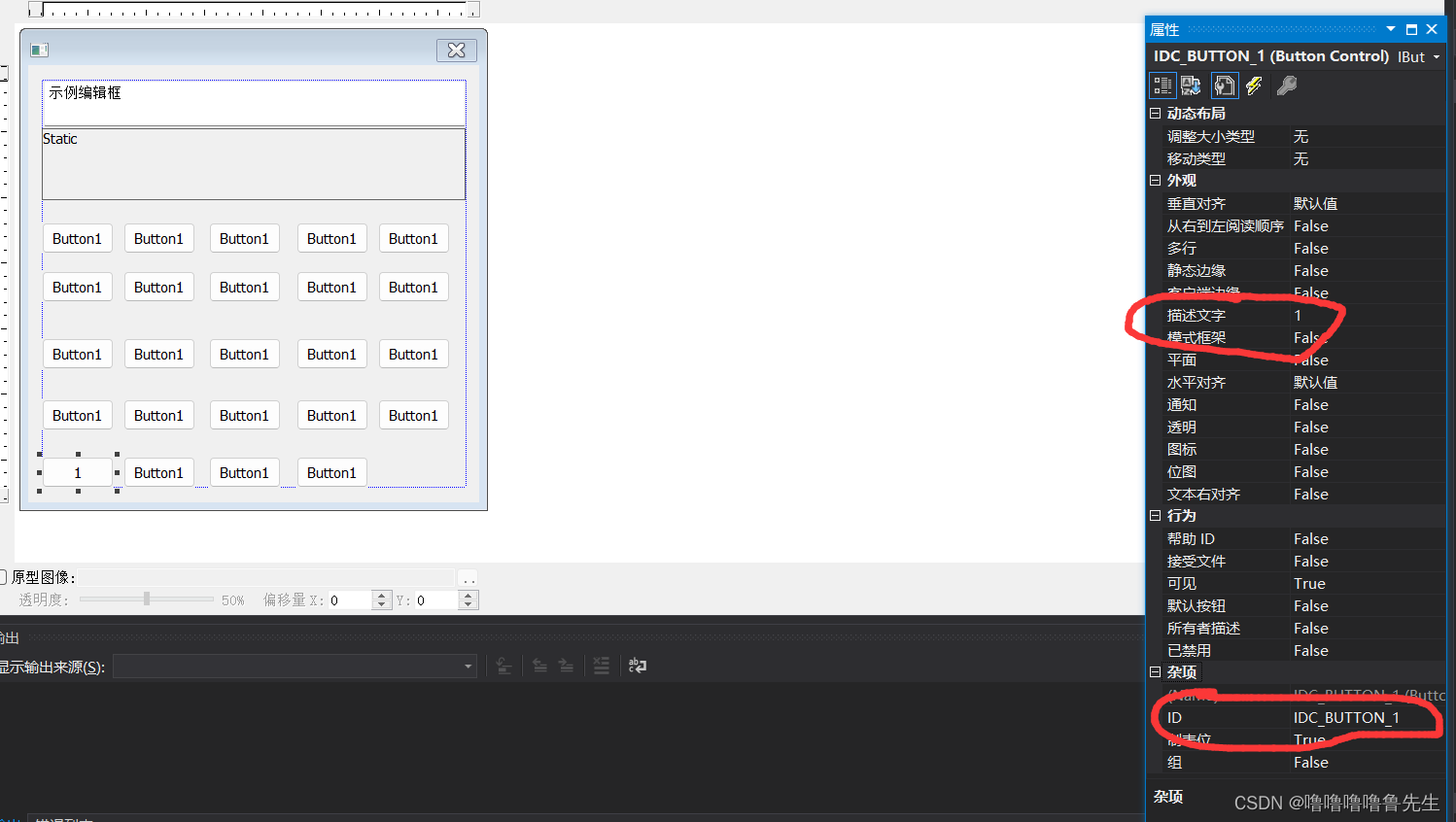
类似的，将其他Button的描述文字和ID进行更改。

以下为我对各按键的ID命名，Button的ID名称影响后续的编程。

2对应ID为IDC_BUTTON_2， 3对应ID为IDC_BUTTON_3，4对应ID为IDC_BUTTON_4 5对应ID为IDC_BUTTON_5， 6对应ID为IDC_BUTTON_6，7对应ID为IDC_BUTTON_7 8对应ID为IDC_BUTTON_8， 9对应ID为IDC_BUTTON_9，0对应ID为IDC_BUTTON_0 +对应ID为IDC_BUTTON_ADD, - 对应ID为IDC_BUTTON_SUB,*对应ID为IDC_BUTTON_MUL, /对应ID为IDC_BUTTON_DIV, |（绝对值符号）对应 ID为IDC_BUTTON_ABS, ^（次方）对应ID为IDC_BUTTON_POW,（对应ID为IDC_BUTTON_LBRACKET， ）对应ID为IDC_BUTTON_RBRACKET,Del（删除按键）对应ID为IDC_BUTTON_DELETE， C（清零按键）对应ID为IDC_BUTTON_CLEAR，1/x（倒数按键）对应ID为IDC_BUTTON_REM，！（阶乘按键）对应ID为IDC_BUTTON_FAC，.（小数点）对应ID为IDC_BUTTON_DOT，=（等于号）对应ID为IDC_BUTTON_EQUAL。

并将Edit Control的ID改为IDC_EDIT_EXP，Static Text的ID改为IDC_STATIC_RESULT

更改完成后，界面如下

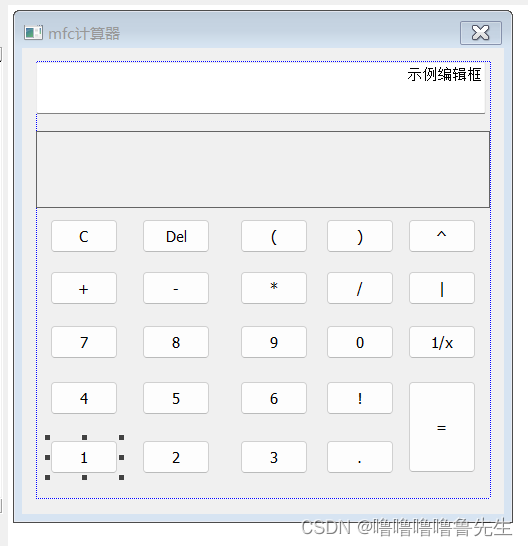
三、对各按键的编写

双击界面中任意一个Button，来到了MFC_CalculatorDlg,cpp文件里面。

在该文件下，找出一个位置，写出按键处理函数

1.事件处理函数

void CMFCCalculatorDlg::AddToEditExp(UINT IDC_Button)
{
    CString strBtn;
    CString strExp;
    GetDlgItem(IDC_Button)->GetWindowText(strBtn);
    GetDlgItem(IDC_EDIT_EXP)->GetWindowText(strExp);
    SetDlgItemText(IDC_EDIT_EXP, strExp + strBtn);
}

2.非特殊按键

然后将各个按键的ID作为函数参数，实现各个Button，例如数字1，2

//‘1’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton1()
{
    AddToEditExp(IDC_BUTTON_1);
}

//‘2’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton2()
{
    AddToEditExp(IDC_BUTTON_2);
}

以上方法用于左括号，有括号，加减乘除，0—9，绝对值，阶乘，次方，小数点的编写。

这些按键的完整代码如下

// 输入区显示按钮操作
void CMFCCalculatorDlg::AddToEditExp(UINT IDC_Button)
{
    CString strBtn;
    CString strExp;
    GetDlgItem(IDC_Button)->GetWindowText(strBtn);
    GetDlgItem(IDC_EDIT_EXP)->GetWindowText(strExp);
    SetDlgItemText(IDC_EDIT_EXP, strExp + strBtn);
}

// ‘（’左括号，按钮事件响应
void CMFCCalculatorDlg::OnBnClickedButtonLbracket()
{
    AddToEditExp(IDC_BUTTON_LBRACKET);
}

// ‘）’右括号，按钮事件响应
void CMFCCalculatorDlg::OnBnClickedButtonRbracket()
{
    AddToEditExp(IDC_BUTTON_RBRACKET);
}

//‘||’绝对值，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButtonAbs()
{
    AddToEditExp(IDC_BUTTON_ABS);
}

//‘！’阶乘，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButtonFac()
{
    AddToEditExp(IDC_BUTTON_FAC);
}

//‘^’幂次方，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButtonPow()
{
    AddToEditExp(IDC_BUTTON_POW);
}

//‘/’除法，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButtonDiv()
{
    AddToEditExp(IDC_BUTTON_DIV);
}

//‘*’乘法，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButtonMul()
{
    AddToEditExp(IDC_BUTTON_MUL);
}

//‘-’减法，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButtonSub()
{
    AddToEditExp(IDC_BUTTON_SUB);
}

//‘+’加法，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButtonAdd()
{
    AddToEditExp(IDC_BUTTON_ADD);
}
//‘.’小数点，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButtonDot()
{
    AddToEditExp(IDC_BUTTON_DOT);
}

//‘0’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton0()
{
    AddToEditExp(IDC_BUTTON_0);
}

//‘1’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton1()
{
    AddToEditExp(IDC_BUTTON_1);
}

//‘2’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton2()
{
    AddToEditExp(IDC_BUTTON_2);
}

//‘3’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton3()
{
    AddToEditExp(IDC_BUTTON_3);
}

//‘4’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton4()
{
    AddToEditExp(IDC_BUTTON_4);
}

//‘5’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton5()
{
    AddToEditExp(IDC_BUTTON_5);
}

//‘6’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton6()
{
    AddToEditExp(IDC_BUTTON_6);
}

//‘7’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton7()
{
    AddToEditExp(IDC_BUTTON_7);
}

//‘8’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton8()
{
    AddToEditExp(IDC_BUTTON_8);
}

//‘9’数字，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButton9()
{
    AddToEditExp(IDC_BUTTON_9);
}

3.特殊按键

（1）清零按键

按键实现代码

void CMFCCalculatorDlg::OnBnClickedButtonClear()
{
    SetDlgItemText(IDC_EDIT_EXP, NULL);
    CString cstr;
    cstr = "0";
    SetDlgItemText(IDC_STATIC_RESULT, cstr);
}

（2）删除按键

void CMFCCalculatorDlg::OnBnClickedButtonDelete()
{
    CString strExp;
    GetDlgItem(IDC_EDIT_EXP)->GetWindowText(strExp);
    strExp = strExp.Left(strExp.GetLength() - 1);
    SetDlgItemText(IDC_EDIT_EXP, strExp);
}

（3）倒数运算

由于倒数运算的特殊性，倒数不参与复合运算。所以可以在倒数按钮函数的上方定义字符串op、double类型数字num1和旗帜变量flag，然后进入函数，利用GetDlgItemText函数获取Eidt Control中的信息，并保存在字符串cs中，令num1等于_ttof(cs)，op等于“1/x”，并将flag置为1。

具体代码如下：

double num1;
double result;
CString op;
int flag = 0;
//倒数，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButtonRem()
{
    CString cs;
    GetDlgItemText(IDC_EDIT_EXP, cs);

    num1 = _ttof(cs);

    op = "1/x";
    flag = 1;
}

（4）等于号按键

等于号按键含有计算结果，包含运算过程中各个函数，较为复杂。

首先在等于号对应函数上方定义一个double类型的结果变量result，进入函数后首先判断flag是否等于1，若等于，则进行倒数运算，否则进行其他运算。代码如下

double result;
//‘=’等于，按钮事件处理
void CMFCCalculatorDlg::OnBnClickedButtonEqual()
{
    if (flag == 1) {
        
        CString cs;
        GetDlgItemText(IDC_EDIT_EXP, cs);
        if (num1 != 0) {
            result = 1 / num1;
        }
        
        cs.Format(_T("%g"), result);
        SetDlgItemText(IDC_STATIC_RESULT, cs);
        flag = 0;
    }

    else {
        CString strExp;
        Calculator cal;        //计算类
        CString cstr_Result;
        CString cstr_ErrorInfo;

        GetDlgItem(IDC_EDIT_EXP)->GetWindowText(strExp);
        string infix(CW2A(strExp.GetString()));
        cal.calculate(infix);
        cstr_Result.Format(_T("%g"), cal.getResult());
        cstr_ErrorInfo + cal.getErrorImfo().c_str();
        if (!cstr_ErrorInfo.IsEmpty()) {
            SetDlgItemText(IDC_STATIC_RESULT, cstr_ErrorInfo);
        }
        SetDlgItemText(IDC_STATIC_RESULT, cstr_Result);
    }
}

可以看出，等于号中包含很多运算函数，接下来一一实现他们。

四、运算函数的实现

1.Calculate.cpp文件

Calculate.cpp文件主要对算术符号的优先权等级，初始化Calculator()函数，表达式自定义标准格式化，获取算术符号优先级，以及计算方法，获取结果等。

代码如下

#include "pch.h"
#include "Calculator.h"

#include <stack>
#include <vector>
#include <string>
#include <cmath>
#include <iostream>

using namespace std;

//算术符号优先权等级
enum PRIO_LV {
    PRIO_LV0 = 0,
    PRIO_LV1 = 1,
    PRIO_LV2 = 2,
    PRIO_LV3 = 3,
    PRIO_LV4 = 4,
};

Calculator::Calculator() {                //构造函数，初始化成员变量

    result = 0.0;
    //cal_ErrorImfo = "";
}

//表达式自定义标准格式化
void Calculator::getFormat(string infix) {

    stdInfix = infix;

    //实现正负数
    //for (int i = 0; i < stdInfix.length(); i++) {                    //string下标调用运算符时可能会导致类型溢出
    for (size_t i = 0; i < stdInfix.size(); i++) {                    //string.size()返回size_type类型，避免下标运算时的类型溢出
        if (stdInfix[i] == '-' || stdInfix[i] == '+') {                //-x转换为0-x，+x转化为0+x
            if (i == 0) {
                stdInfix.insert(0, 1, '0');
            }
            else if (stdInfix[i - 1] == '(') {
                stdInfix.insert(i, 1, '0');
            }
        }
    }
}

//获取算术符号优先级
int Calculator::getPrior(char c) {

    if (c == '+' || c == '-') {
        return PRIO_LV1;
    }
    else if (c == '*' || c == '/') {
        return PRIO_LV2;
    }
    else if (c == '%' || c == '^') {
        return PRIO_LV3;
    }
    else if (c == '！') {
        return PRIO_LV4;
    }
    else {
        return PRIO_LV0;
    }
    string str = "非法符号";
    cout << str << endl;

}

//计算方法
void Calculator::calculate(string infix) {
    getFormat(infix);            //表达式自定义标准格式化
    getPostfix();                //后缀表达式转换
    calResult();                //计算结果
}

//获取结果
double Calculator::getResult() {
    return result;
}

2.GetCalResult.cpp文件

GetCalResult.cpp文件主要是获取计算结果。

代码如下：

#define _CRT_SECURE_NO_WARNINGS
#include "pch.h"
#include "Calculator.h"

#include <stack>
#include <vector>
#include <string>
#include <cmath>
#include <iostream>

void Calculator::calResult() {

    string tmp;
    double number = 0;
    double op1 = 0, op2 = 0;

    for (int i = 0; i < postfix.size(); i++) {
        tmp = postfix[i];
        if (tmp[0] >= '0' && tmp[0] <= '9') {
            number = atof(tmp.c_str());
            figStack.push(number);
        }
        else if (postfix[i] == "+") {
            if (!figStack.empty()) {
                op2 = figStack.top();
                figStack.pop();
            }
            if (!figStack.empty()) {
                op1 = figStack.top();
                figStack.pop();
            }
            figStack.push(op1 + op2);
        }
        else if (postfix[i] == "-") {
            if (!figStack.empty()) {
                op2 = figStack.top();
                figStack.pop();
            }
            if (!figStack.empty()) {
                op1 = figStack.top();
                figStack.pop();
            }
            figStack.push(op1 - op2);
        }
        else if (postfix[i] == "*") {
            if (!figStack.empty()) {
                op2 = figStack.top();
                figStack.pop();
            }
            if (!figStack.empty()) {
                op1 = figStack.top();
                figStack.pop();
            }
            figStack.push(op1 * op2);
        }
        else if (postfix[i] == "/") {
            if (!figStack.empty()) {
                op2 = figStack.top();
                figStack.pop();
            }
            if (!figStack.empty()) {
                op1 = figStack.top();
                figStack.pop();
            }
            if (op2 != 0) {
                ///除数不为0，未做处理，默认
            }
            figStack.push(op1 / op2);
        }
        else if (postfix[i] == "^") {
            if (!figStack.empty()) {
                op2 = figStack.top();
                figStack.pop();
            }
            if (!figStack.empty()) {
                op1 = figStack.top();
                figStack.pop();
            }
            figStack.push(pow(op1, op2));
        }
        else if (postfix[i] == "|") {
            if (!figStack.empty()) {
                op1 = figStack.top();
                figStack.pop();
            }
            figStack.push(abs(op1));
        }
        else if (postfix[i] == "!") {
            if (!figStack.empty()) {
                op1 = figStack.top();
                figStack.pop();
            }
            if (op1 > 0) {
                //阶乘数应大于；为小数时(转化为整数求阶)
                double factorial = 1;
                for (int i = 1; i <= op1; ++i)
                {
                    factorial *= i;
                }
                op1 = factorial;
            }
            figStack.push(op1);
        }
    }//end for
    if (!figStack.empty()) {
        result = figStack.top();
    }
}

3.transform.cpp文件

transform.cpp文件主要是将中缀表达式转化为后缀表达式，该文件也是整个工程最为重要最为复杂的一部分，这里我们着重介绍。

对于一般的，在数学上的，所有的计算表达式均是中缀表达式（这体现在运算符号一般在数字的中间），如对于表达式2+3，其中的加号在数字2，3的中间。将其转化为后缀表达式就是2 3 + ，体现在加号在两个运算数的后面。

** 计算机是执行命令的机器，对于中缀表达式，当表达式中有括号，乘法，加法等的复合运算，计算机就需要多次遍历表达式，从而先计算括号等优先级较高的运算符，因此将会大大降低运算效率，所以人们发明出后缀表达式，只需从左向右遍历一遍即可，**契合计算机，提高了运算效率。

** 计算机从左向右遍历表达式，遇到数字进栈，遇到运算符就退出栈中两个数字，先退出的在运算符前面，后退出在运算符后面，进行计算，然后将运算结果压入栈中，继续遍历表达式，最终栈中就有一个数字，就为运算结果。**

代码如下：

#include "pch.h"
#include "Calculator.h"

#include <stack>
#include <vector>
#include <string>
#include <cmath>
#include <iostream>

//绝对值符号个数的奇偶性
enum ABS_ODEVITY {
    ABS_ODD = 1,
    ABS_EVEN = 2,
};
void Calculator::getPostfix() {

    int absNumeber = ABS_ODD;                //绝对值符号个数的奇偶性
    string tmp;

    //for (int i = 0; i < stdInfix.length(); i++) {
    for (size_t i = 0; i < stdInfix.size(); i++) {                    //string.size()返回size_type类型，避免下标运算时的类型溢出
        tmp = "";
        switch (stdInfix[i]) {
        case '+':
        case '-':
        case '*':
        case '/':
        case '^':
        case '!':
            if (symStack.empty() || symStack.top() == '(' || symStack.top() == '[' || symStack.top() == '{' || (symStack.top() == '|' && absNumeber == ABS_ODD)) {
                symStack.push(stdInfix[i]);
            }
            else {
                while (!symStack.empty() && (getPrior(symStack.top()) >= getPrior(stdInfix[i]))) {
                    tmp += symStack.top();
                    postfix.push_back(tmp);
                    symStack.pop();
                    tmp = "";
                }
                symStack.push(stdInfix[i]);
            }
            break;
        case '|':
            if (absNumeber == ABS_ODD) {
                symStack.push(stdInfix[i]);
                absNumeber = ABS_EVEN;
            }
            else {
                while (!symStack.empty() && symStack.top() != '|') {
                    tmp += symStack.top();
                    postfix.push_back(tmp);
                    symStack.pop();
                    tmp = "";
                }
                if (!symStack.empty() && symStack.top() == '|') {
                    tmp += symStack.top();
                    postfix.push_back(tmp);                        //左绝对值符号'|'加入后缀表达式，用于绝对值的检测计算
                    symStack.pop();
                    absNumeber = ABS_ODD;
                }
            }
            break;
        case '(':
        case '[':
        case '{':
            symStack.push(stdInfix[i]);
            break;
        case ')':
            while (!symStack.empty() && symStack.top() != '(') {
                tmp += symStack.top();
                postfix.push_back(tmp);
                symStack.pop();
                tmp = "";
            }
            if (!symStack.empty() && symStack.top() == '(') {
                symStack.pop();                            //将左括号出栈丢弃
            }
            break;
        case ']':
            while (!symStack.empty() && symStack.top() != '[') {
                tmp += symStack.top();
                postfix.push_back(tmp);
                symStack.pop();
                tmp = "";
            }
            if (!symStack.empty() && symStack.top() == '[') {
                symStack.pop();                            //将左括号出栈丢弃
            }
            break;
        case '}':
            while (!symStack.empty() && symStack.top() != '{') {
                tmp += symStack.top();
                postfix.push_back(tmp);
                symStack.pop();
                tmp = "";
            }
            if (!symStack.empty() && symStack.top() == '{') {
                symStack.pop();                            //将左括号出栈丢弃
            }
            break;
        default:
            if ((stdInfix[i] >= '0' && stdInfix[i] <= '9')) {
                tmp += stdInfix[i];
                while (i + 1 < stdInfix.length() && (stdInfix[i + 1] >= '0' && stdInfix[i + 1] <= '9' || stdInfix[i + 1] == '.')) {        //小数处理

                    tmp += stdInfix[i + 1];            //是连续的数字，则追加
                    i++;
                }
                if (tmp[tmp.length() - 1] == '.') {
                    tmp += '0';                        //将x.做x.0处理
                }
                postfix.push_back(tmp);
            }
            break;
        }
    }

    //if(!symStack.empty()) {
    while (!symStack.empty()) {                        //将栈中剩余符号加入后缀表达式
        tmp = "";
        tmp += symStack.top();
        postfix.push_back(tmp);
        symStack.pop();
    }
}

4.Calculator.h 文件（头文件）

代码如下：

#pragma once

#include <stack>
#include <vector>
#include <string>
using namespace std;

//计算器类
class Calculator
{
public:
    Calculator();
    void calculate(string infix);        //计算方法
    void getFormat(string infix);        //表达式自定义标准格式化
    int getPrior(char c);                //获取算术符号优先级
    void getPostfix();                    //后缀表达式转换
    void calResult();                    //计算结果
    double getResult();                    //获取结果
    string operatorSym;                    //运算符号

private:
    vector<string> postfix;                //后缀表达式向量
    stack<char> symStack;                //符号栈
    stack<double> figStack;                //数字栈
    string stdInfix;                    //自定义标准格式化表达式
    double result;                        //最终计算结果
};

五、计算示例

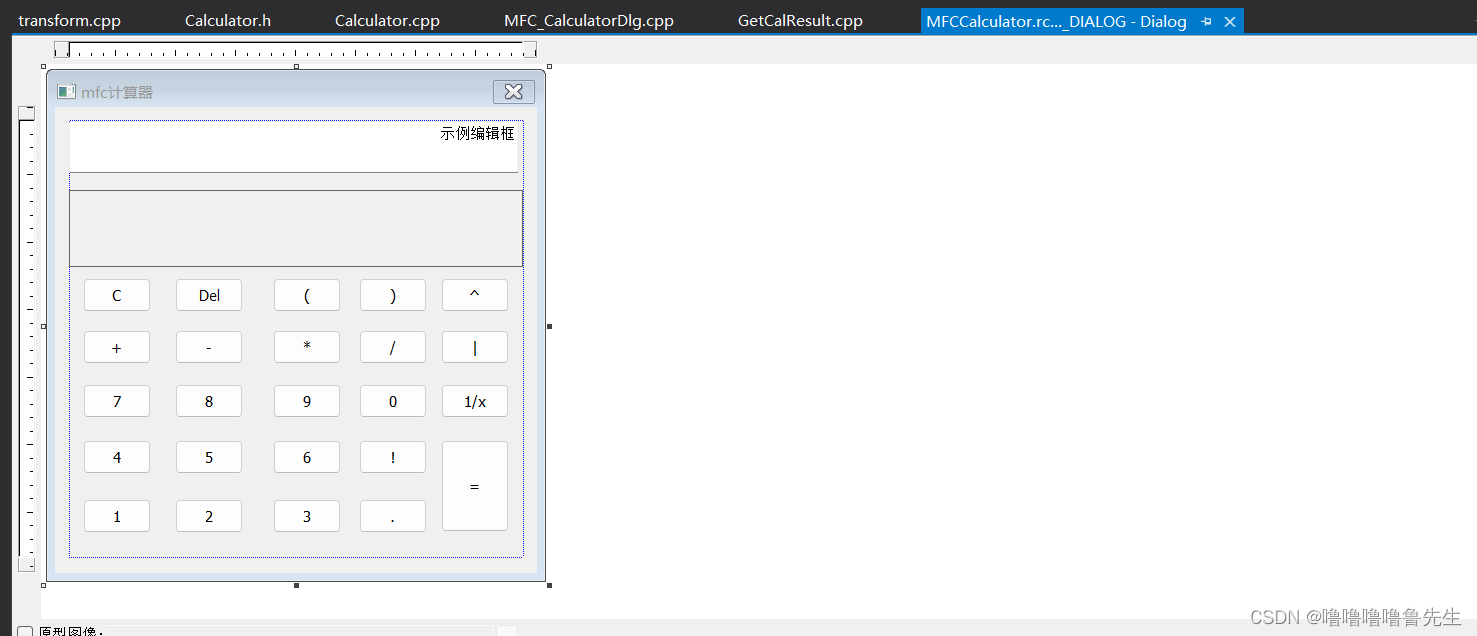
普通的复合运算

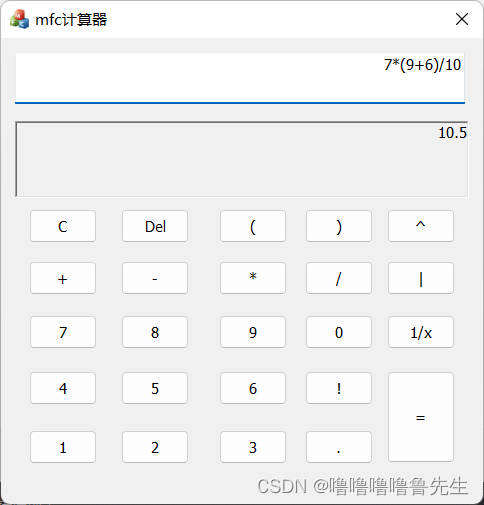
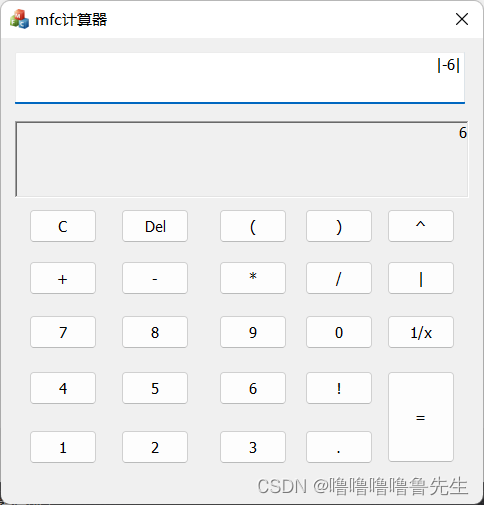
绝对值，倒数，次方的运算

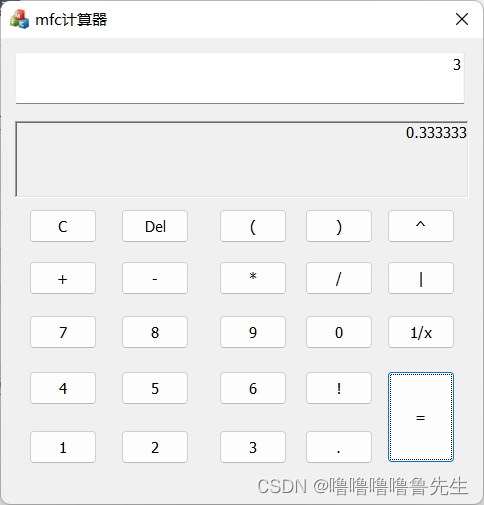
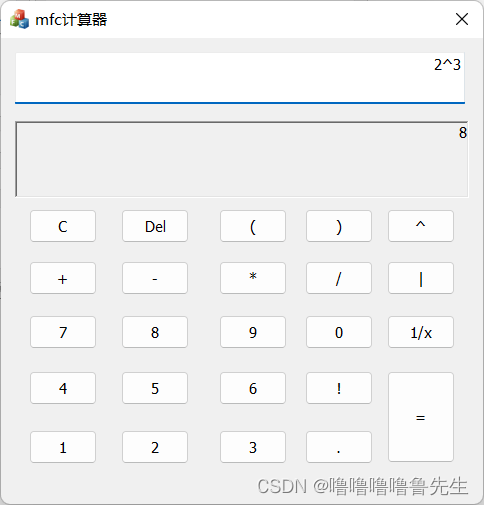
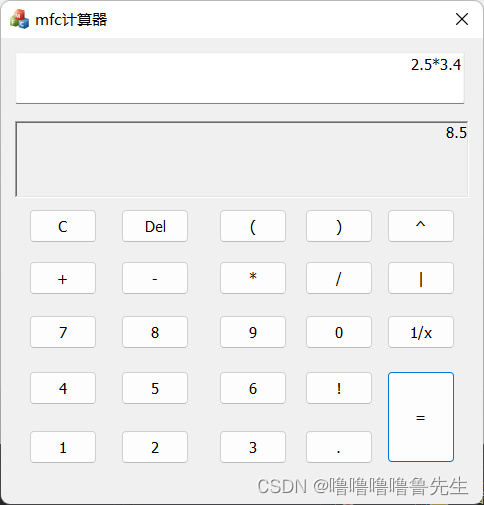
小数的运算

标签： mfc c++ 小程序
本文转载自: https://blog.csdn.net/m0_57950108/article/details/126004401
版权归原作者 噜噜噜噜鲁先生 所有， 如有侵权，请联系我们删除。
登录后发布评论

“MFC计算器——万字长文/一看就懂（需要的建议点赞收藏）”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

如何给SaaS应用做安全

【软件测试】自动化常用函数

postman变量和脚本功能介绍

Python Selenium常见的报错以及措施

idea导出配置文件

如何在visual studio中 生成 并 使用dll和lib文件

Docker homeassistant 反向代理 外网访问

文章导航