《并行计算》求解线性方程组

文章目录

三角形方程组的求解

上三角方程组的求解

这个类型的方程组求解算是最简单的了！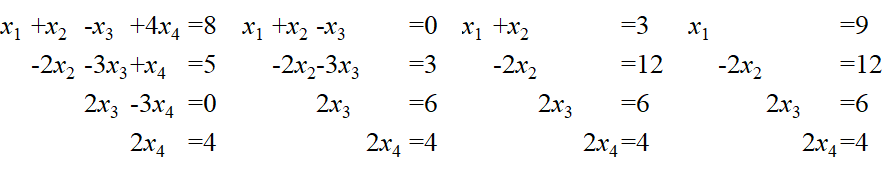

可以用时间复杂度为平方级的串行算法求解：

看一下上面的串行算法，第2个循环（内层循环）是可以并行的，因此有如下线性级的并行算法：
（将p个处理器行循环带状划分）

三对角方程组的求解

我们先约定一些符号：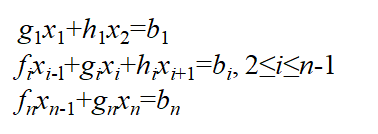

也就是系数矩阵一行最多的三个非零元素，首非零元记为

f

，第二个非零元记为

g

，第三个非零元记为

h

。

下面是求解这种类型方程组的一个例子：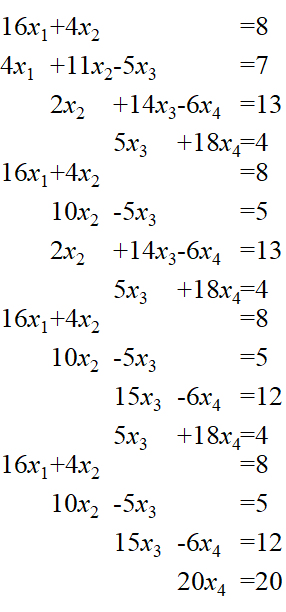

可以看到，这种方法将三对角变换成了上三角，从而用前面的方法做。

串行算法可以达到线性，但难以再并行化

为了更快，我们引入奇偶求解法，上例示：

下面讨论的都是一般的方程组形式了

稠密线性方程组的求解

有回代的高斯消去法

求解分为消元和回代两个阶段，最终还是转换为上三角

消元过程中应用选主元方法，增强算法数值稳定性

无回代的高斯消去法

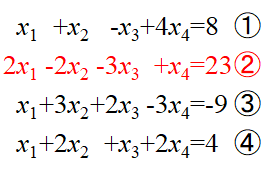
与有回代高斯约旦消元法不同的是，这里每一步消元的时候，所有式子都参与了消元运算，而有回代法是只针对特定式子消元，对比一下就知道了。

并行算法：

稀疏线性方程组的求解

雅可比迭代法

模拟一下：

高斯-赛德尔迭代法

这个应该不会考了吧，等我后面再来看

Appendix

// 计算二元一次方程组#include<iostream>#include<stdio.h>usingnamespace std;intmain(){
    cout <<"input first fomular params: ";double a11, a12, b1;
    cin >> a11 >> a12 >> b1;
    cout <<"input second fomular params: ";double a21, a22, b2;
    cin >> a21 >> a22 >> b2;double x1, x2;
    x1 =(b1-(a12*b2)/a22)/(a11-(a12*a21)/a22);
    x2 =(b1-(a11*b2)/a21)/(a12-(a11*a22)/a21);
    cout <<"x1="<< x1 << endl;
    cout <<"x2="<< x2 << endl;getchar();return0;}