参考大佬文章,收益匪浅
因为这是课内实验,所以我并没有把所有代码都上传,参考的文章里代码很全。
实验目的
- 掌握AES算法能量迹构造;
- 掌握AES算法CPA攻击基本原理。
实验人数
每组1人
系统环境
Windows
实验原理
CPA是利用密码芯片的假设模型,预测其加解密时的功耗大小,然后和实际测量的功耗大小进行相关性分析推测密钥。CPA攻击通常采用汉明重量模型,所谓汉明权重就是一个码字中1码元的总数目,汉明权重越大,芯片运算时的功耗就越大。
实验内容
- Readfile-student.py:AES 能耗波形文件读入与存储,“Save2Npy”函数输出能量迹trace数据。- 分析程序读入的pts、pcts、pns分别是什么数据,类型是什么,维数是多少
- CPA-student.py:根据汉明重量模型恢复16个字节密钥。- 补充相关系数的计算代码,并取最大值记为maxcpa- 解释每个生成图像的含义(横纵坐标、波形、尖峰等)- 打印输出恢复的所有正确密钥bestguess
- 分析能量迹对密钥恢复的影响:10、50、100、150、200、240条能量迹能够恢复的正确密钥的字节数和位置分别是什么,并分析其原因。
实验步骤
pts、pcts、pns分别是什么数据、类型、维数
pts

图6.1 pts部分数据
数据:明文
类型:数组
维数:二维(250,16)
pcts

图6.2 pcts部分数据
数据:明文,密文
类型:数组
维数:三维(250,2,16)
pns

图6.3 pns部分数据
数据:能量迹纵坐标
类型:数组
维数:二维(250,10000)
完善相关系数的计算代码
hwlist = np.zeros(numtraces)
语句之前的代码是程序自带的,最外层的for循环的目的是遍历密钥的字节位置,第二层的for循环是遍历所有密钥的可能性。本次实验需要使用能量迹的明文和密钥异或运算并执行后续代码,所以还需要设置一层循环,使得对应设置数量的能量迹明文可以和密钥进行运算,求得汉明重量,代码如下。
hwlist = np.zeros(numtraces)#初始化数组for tnum inrange(0, numtraces):
hwlist[tnum]= HW[intermediate(pt[tnum][bnum], kguess)]
注意一点pt二维数组(程序另有设置明文数组为pt)的取值,pts明文数组中250表示明文数量,而16是明文的size,所以明文数组长度为16。
因为是汉明重量模型,按照以往实验的思路,下一步是根据相关系数计算公式
r
i
,
j
=
∑
d
=
1
D
[
(
h
d
,
i
−
h
i
‾
)
(
t
d
,
j
−
t
j
‾
)
]
∑
d
=
1
D
(
h
d
,
i
−
h
i
‾
)
2
∑
d
=
1
D
(
t
d
,
j
−
t
j
‾
)
2
{r_{i,j}} = \frac{{\sum\nolimits_{d = 1}^D {\left[ {\left( {{h_{d,i}} - \overline {{h_i}} } \right)\left( {{t_{d,j}} - \overline {{t_j}} } \right)} \right]} }}{{\sqrt {\sum\nolimits_{d = 1}^D {{{\left( {{h_{d,i}} - \overline {{h_i}} } \right)}^2}} \sum\nolimits_{d = 1}^D {{{\left( {{t_{d,j}} - \overline {{t_j}} } \right)}^2}} } }}
ri,j=∑d=1D(hd,i−hi)2∑d=1D(td,j−tj)2∑d=1D[(hd,i−hi)(td,j−tj)]
推导出逻辑代码。
这部分代码我之前有写过,不过那时公式逻辑代码组成的函数输入对象虽然也是数组(准确来说应该说是列表),但是体量没有这次仿真实验做的大,而且numpy函数生成的数组在类型上就和列表就不一样,所以代码需要重新编写。为了代码流程显得模块化,我将上述计算公式模块化如下:
r
i
,
j
=
m
o
l
e
s
u
m
d
e
n
s
u
m
1
×
d
e
n
s
u
m
2
{r_{i,j}} = \frac{molesum}{\sqrt{densum1 \times densum2}}
ri,j=densum1×densum2molesum
- 第一步依旧是是初始化,只不过是数组的初始化;
# 初始化数组——简化计算流程molesum = np.zeros(numpoint)densum1 = np.zeros(numpoint)densum2 = np.zeros(numpoint) - 第二步理论上来说可以直接运算了,不过先计算平均值可以减少代码冗余。分别计算假设值和轨迹上所有点的汉明重量的平均值。
#当前猜测密钥参与运算的汉明总量数组均值h_mean = np.mean(hwlist, dtype=np.float64)#采集线上的电压均值,共10000份t_mean = np.mean(traces, axis=0, dtype=np.float64) - 第三步开始正式计算,累加次数取决于使用的能量迹数量,计算结束后将相关系数的最大绝对值存入maxcpa列表中。
for i inrange(0, numtraces): h =(hwlist[i]- h_mean) t = traces[i]- t_mean molesum = molesum +(h * t) densum1 = densum1 + h * h densum2 = densum2 + t * t maxcpa[kguess]=max(abs(molesum / np.sqrt(densum1 * densum2)))可能陌生的地方就是第三行的t值,其实t在这里是个数组,这一行的代码运算也是数组之间的运算。 图6.5 一维数组t
图6.5 一维数组t  图6.5 二维数组traces 第三行代码还可以替换为
图6.5 二维数组traces 第三行代码还可以替换为t = traces[i,:] - t_mean - 将256种密钥遍历测试后,将maxcpa列表中的最大值储存,作为所猜测的当前密钥字节数值。
bestguess[bnum]= np.argmax(maxcpa)
完整代码如下(打印语句不放):
for bnum inrange(0,16):#bnum定义所攻击的字节位置
maxcpa =[0]*256#记录cpa最大值的向量for kguess inrange(0,256):#补充相关系数的计算代码,并取最大值记为maxcpa#计算猜测密钥参与运算形成的汉明重量
hwlist = np.zeros(numtraces)#初始化数组for tnum inrange(0, numtraces):
hwlist[tnum]= HW[intermediate(pt[tnum][bnum], kguess)]# 根据相关系数计算公式推导出逻辑代码# 初始化数组——简化计算流程
molesum = np.zeros(numpoint)
densum1 = np.zeros(numpoint)
densum2 = np.zeros(numpoint)#当前猜测密钥参与运算的汉明总量数组均值
h_mean = np.mean(hwlist, dtype=np.float64)#采集线上的电压均值,共10000份
t_mean = np.mean(traces, axis=0, dtype=np.float64)#正式计算for i inrange(0, numtraces):
h =(hwlist[i]- h_mean)
t = traces[i]- t_mean
molesum = molesum +(h * t)
densum1 = densum1 + h * h
densum2 = densum2 + t * t
maxcpa[kguess]=max(abs(molesum / np.sqrt(densum1 * densum2)))
bestguess[bnum]= np.argmax(maxcpa)
程序运行结果
正确密钥bestguess打印输出如下(使用能量迹为250条):

图6.6 正确密钥—250条能量迹
生成图像如下:
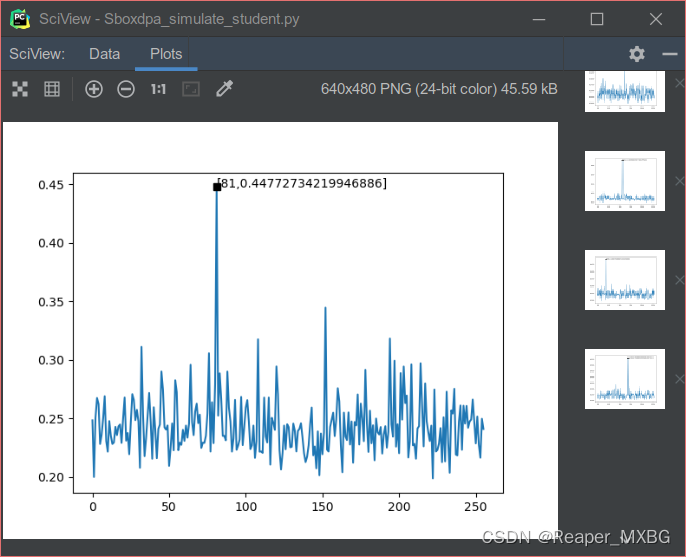
图6.7 仿真能量迹-250条能量迹数据
分析图像的含义
以此图为例:
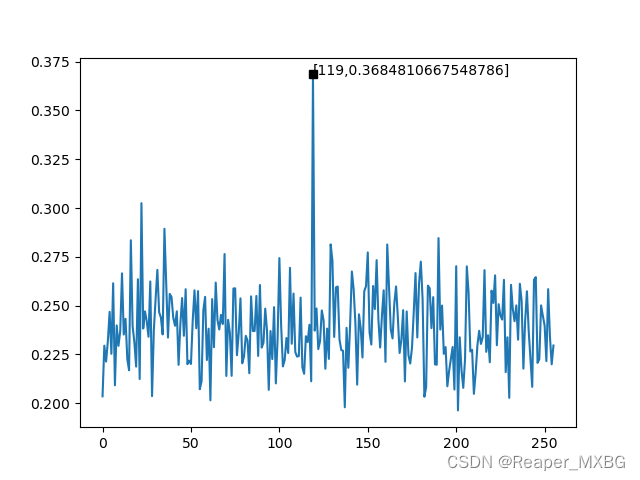
图6.8 仿真能量迹-50条能量迹
横坐标:所有可能的密钥
纵坐标:相关系数绝对值
波形:波形可以反映算法的处理周期和处理速度
尖峰:在此实验中,尖峰代表着猜测密钥和正确结果的相关性,尖峰值越大,相关性越高
分析能量迹对密钥恢复的影响
分别采用10、50、100、150、200、240条能量迹。
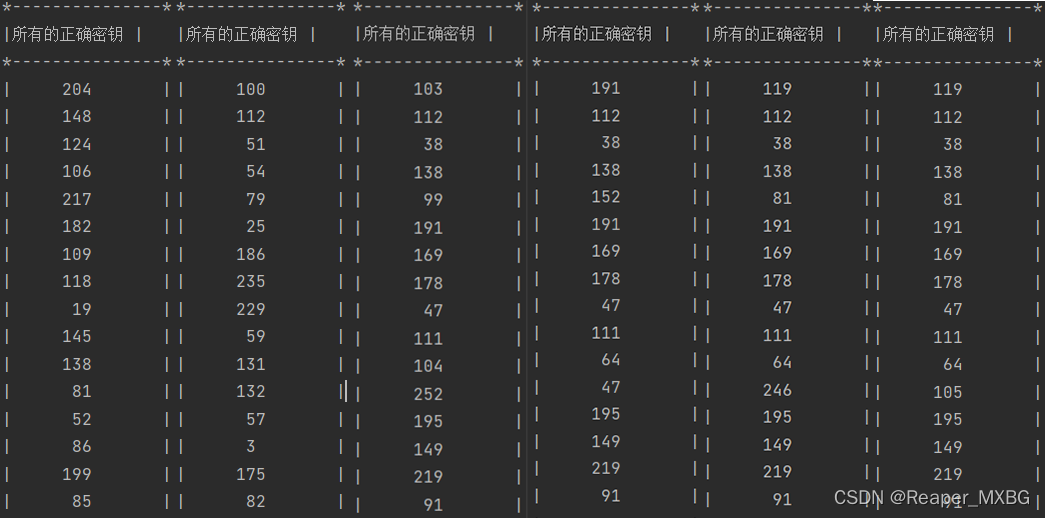
图6.9 六种情况仿真能量迹
以250条能量迹的正确密钥输出为正确标准,对此六种情况下的正确密钥输出进行判定,结果如下。
能量迹条数恢复正确密钥字节数正确密钥位置(0起始)100无5011100121,2,3,5,6,7,8,9,12,13,14,15150131,2,3,5,6,7,8,9,10,12,13,14,15200150,1,2,3,4,5,6,7,8,9,10,12,13,14,1524016全部
原因简单来说就是,参考基础不够大,无法生成普适规律。参考基数越大,个例对整体判断的影响越小;反之,越大。
思考问题
如果利用比特模型和汉明距离模型,应该如何进行攻击?
汉明距离模型
计算数字电路在某个特定时段内,0→1转换和1-→0转换的总数。然后,利用转换的总数来刻画电路在该时段内的能量消耗。把对整个电路的仿真划分为小的时间段,就可以生成一-种能量迹。这种能量迹中不包含具体的电压值,而是包含每个时间段内电路发生转换的次数。
比特模型
攻击者通过侧信道可以得到密码算法中间状态的某个比特,将该侧信道泄露的消息与立方攻击相结合从而恢复密钥信息。
总结
收获之一就是明白了在给定能量迹数据集的条件下,如何进行仿真实验。
前两次侧信道仿真实验使用的n个明文其实代表的就是n条明文的意思,而不是一条明文里的n个数据,这点不弄懂是没法继续理解的。然后要明确的点是明文整体和密钥进行异或,不会出现部分字节不异或的情况,所以这种思想带入AES的CPA仿真实验中的结果就是,参与运算的每个能量迹,轮到取第几位时统一采集,逐个和猜测密钥异或并计算汉明重量形成长度为明文数量的数组;相同的,能量迹的电压值也是需要纵向划分数组,用图片理解这里纵向划分的意义:
pic_center
图8.1 能量迹数据集结构图
这是能量迹数据的结构示意图,每条明文都有属于自己的n个采集的电压值(黑色线段),之前明文被采集和密钥异或其实也是纵向划分,和这个结构是一样的。比如取每条明文的第一个字节/电压值,就是在纵轴方向上把每条明文的第一项数据切割出来,这样就形成两个具有线性关系的整体,汉明重量数组和电压值数组,然后两个整体去计算相关系数,顺理成章地完成了仿真实验流程。
这么看起来其实也没什么难的,原理看似很简单,其实真的简单,但是简单却不一定能理解,做前两次仿真实验时以为自己懂了,到了最后一次实验数据“正规“后,往常不是很清晰的知识点就会拖累实验进度,等再次搞懂后,发现其实并没有一开始做时那么难。
之前的仿真实验都是基于白盒的仿真实验,S盒的运算公式和盒内部数值都是公开的,所以相对容易。这次实验比之前的实验从更正规的方式去做了一遍仿真实验,看到仿真能量迹画出来的时候还是很激动的。
注意点:
代码逻辑上我觉得重点要理解的就是“两层循环嵌套”,即最外层的密钥16字节循环 + 遍历密钥循环,至于剩下的都是小循环而已,不对整体结构上产生影响。
还有要理解能量迹数据的各个属性,虽然在代码中能量迹数据看起来很轻松的就被调用使用,但是难点是在将能量迹数据从文件中提取出来时知道其中是什么数据,怎么用,何时用。
版权归原作者 Reaper_MXBG 所有, 如有侵权,请联系我们删除。