为什么前端数值精度会丢失?(BigInt解决办法)

    相信各位前端小伙伴在日常工作中不免会涉及到使用 JavaScript 处理 数值 相关的操作，例如 **数值计算、保留指定小数位、接口返回数值过大** 等等，这些操作都有可能导致原本正常的数值在 JavaScript 中确表现得异常（即 精度丢失）。

精度丢失场景

浮点数的计算

1、加法和减法

0.1 + 0.2 // 结果为 0.30000000000000004
0.3 - 0.1 // 结果为 0.19999999999999996

// 这是因为浮点数的二进制表示无法准确表示某些十进制小数，导致计算结果存在微小的误差。

2、乘法和除法

0.1 * 0.2 // 结果为 0.020000000000000004
0.3 / 0.1 // 结果为 2.9999999999999996

// 在进行乘法和除法时，浮点数计算结果的精度问题更为突出，可能会产生更大的误差。

3、比较运算

0.1 + 0.2 === 0.3 // 结果为 false

// 直接比较浮点数可能会导致不准确的结果，因为计算结果的微小误差可能使它们不完全相等。

超过最值

    所谓 **超过最值（

最大、最小值

）** 指的是超过了 **

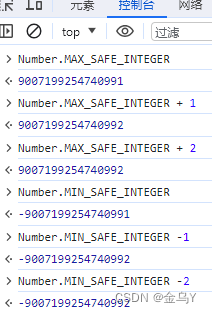
Number.MIN_SAFE_INTEGER（- 9007199254740991）

，即 +（2^53 – 1）** 或 **

Number.MAX_SAFE_INTEGER（+ 9007199254740991）

，即 -（2^53 – 1）** 范围的值，项目中最常见的就是如下几种情况：1

• 1、后端返回的数值超过最值- 例一，后端返回的列表数据，通常都会有相应的 ID 来标识唯一性，但后端生成这个 ID 时是 Long 类型，那么该值很可能就会超过 JavaScript 中能表示的最大正整数，此时就导致精度丢失，即前端实际获取到的 ID 值和后端返回的将不一致。- 例二，后端可能需要将一些值通过计算之后，把对应的结果值返回给前端，此时若该值超过了 最值，那么也会产生精度丢失。
• 2、前端进行数值计算时，计算结果超过最值

保留指定小数位

    除了上述对涉及浮点数计算、超过最值的场景之外，我们通常还会对数值进行保留指定小数位的处理，而部分开发者可能会直接使用 **Number.prototype.toFixed** 来实现，但这个方法却并不能保证我们期望的效果，例如保留小数位时需要进行 **四舍五入** 时就会有问题，如下：

console.log(1.595.toFixed(2)) // 1.59 ——> 期望为：1.60
console.log(1.585.toFixed(2)) // 1.58 ——> 期望为：1.59
console.log(1.575.toFixed(2)) // 1.57 ——> 期望为：1.58
console.log(1.565.toFixed(2)) // 1.56 ——> 期望为：1.57
console.log(1.555.toFixed(2)) // 1.55 ——> 期望为：1.56
console.log(1.545.toFixed(2)) // 1.54 ——> 期望为：1.55
console.log(1.535.toFixed(2)) // 1.53 ——> 期望为：1.54
console.log(1.525.toFixed(2)) // 1.52 ——> 期望为：1.53
console.log(1.515.toFixed(2)) // 1.51 ——> 期望为：1.52
console.log(1.505.toFixed(2)) // 1.50 ——> 期望为：1.51

精度丢失的原因

计算机内部实际上只能 存储/识别 **

二进制

**，因此 文档、图片、数字 等都会被转换为 二进制，而对于数字而言，虽然我们看到的是 十进制 的表示结果，但实际上会底层会进行 十进制 和 二进制 的相互转换，而这个转换过程就有可能会出现 精度丢失，因为十进制转二进制后可能产生 无限循环 部分，而 实际存储空间是有限的。

由于计算机内部使用二进制浮点数表示法，而不是十进制。这种二进制表示法在某些情况下无法准确地表示某些十进制小数，从而导致精度丢失，如：

1、无法精确表示的十进制小数：

    某些十进制小数无法准确地表示为有限长度的二进制小数。例如，0.1 和 0.2 这样的十进制小数在二进制表示中是无限循环的小数，因此在计算机内部以有限的位数进行表示时，会存在舍入误差，导致精度丢失。

2、舍入误差：

    由于浮点数的位数是有限的，对于无法精确表示的十进制小数，计算机进行舍入来逼近其值。这种舍入操作会引入误差，并导致计算结果与预期值之间的差异。

    Number.prototype.toFixed 的舍入：关于这个方法的舍入方式，目前最多的说法就是 银行家算法 ，的确在大多情况下确实能够符合 银行家算法 的规则，但是部分情况就并不符合其规则，因此严格意义上来讲 Number.prototype.toFixed 并不算是使用了 银行家算法。（**银行家舍入：所谓银行家舍入法，其实质是一种四舍六入五取偶（又称四舍六入五留双）法。** 简单来说就是：四舍六入五考虑，五后非零就进一，五后为零看奇偶，五前为偶应舍去，五前为奇要进一。具体解释见下文） 

3、算术运算的累积误差：

    在进行一系列浮点数算术运算时，舍入误差可能会累积并导致精度丢失。每一次运算都会引入一些误差，这些误差在多次运算中逐渐累积，导致最终结果的精度降低。

4、比较运算的不精确性：

    由于浮点数的表示精度有限，直接比较浮点数可能会导致不准确的结果。微小的舍入误差可能使得两个看似相等的浮点数在比较时被认为是不等的。

5、数值范围的限制：

    浮点数的表示范围是有限的，超出范围的数值可能会导致溢出或下溢，进而影响计算结果的精度。

银行家算法

所谓银行家算法用一句话概括为：
**四舍六入五考虑，

五后

有数

就进一

，

五后

无数 看

奇偶

，

五前

为偶当

舍去

，

五后

为奇要

进一

**

• 四舍 指保留位后的 数值 < 5 应 舍去，4 只是个代表值
• 六入 指保留位后的 数值 > 5 应 进一，6 只是个代表值
• 若保留位后的 数值 = 5，看 5 后 是否有数 - 若 5 后 无数，则看 5 前 的数值的 奇偶 来判断 - 若 5 前 的数值为 偶数，则 舍去- 若 5 前 的数值为 奇数，则 进一- 若 5 后 有数，则 进一

// 四舍
(1.1341).toFixed(2) = '1.13'

// 六入
(1.1361).toFixed(2) = '1.14'

// 五后 有数 ，进一
(1.1351).toFixed(2) = '1.14'

// 五后 无数，看奇偶，五前为 3 奇数，进一 
(1.1350).toFixed(2) = '1.14'

// 五后 无数，看奇偶，五前为 0 偶数，舍去
(1.1050).toFixed(2) = '1.10'

这样看起来没啥问题，但是：

// 五后 有数，应进一
(1.1051).toFixed(2) = 1.11 （正确 √）
(1.105).toPrecision(17) = '1.1050000000000000' // 精度

// 五后 无数，看奇偶，五前为 0 偶数，应舍去
(1.105).toFixed(2) = 1.10 （正确 √）

// 五后 无数，看奇偶，五前为 2 偶数，应舍去
(1.125).toFixed(2) = 1.13 （不正确 ×）
1.125.toPrecision(17) = '1.1250000000000000' // 精度

// 五后 无数，看奇偶，五前为 4 偶数，应舍去
(1.145).toFixed(2) = 1.15 （不正确 ×）
1.145.toPrecision(17) = '1.1450000000000000' // 精度

// 五后 无数，看奇偶，五前为 6 偶数，应舍去
(1.165).toFixed(2) = 1.17 （不正确 ×）
1.165.toPrecision(17) = '1.1650000000000000' // 精度

// 五后 无数，看奇偶，五前为 8 偶数，应舍去
(1.185).toFixed(2) = 1.19 （不正确 ×）
1.185.toPrecision(17) = '1.1850000000000001' // 精度

ECMAScript 定义的 toFixed 标准

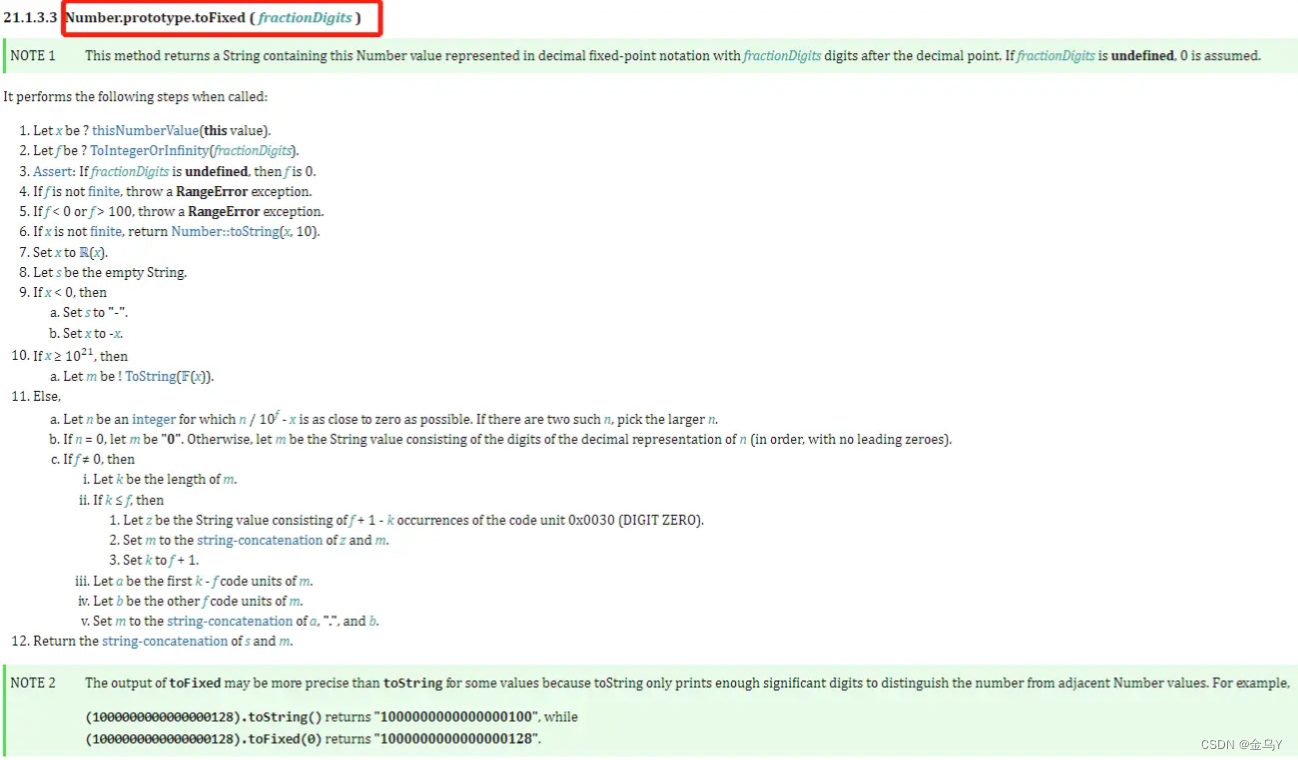
简单解释一下：

1. 让 x = 目标数字，如：**(1.145).toFixed(2)** 中 x = 1.145 。
2. 让 f = 参数，如：**(1.145).toFixed(2)** 中 f = 2 。
3. 若 **f = undefined**，即 未传参，则将 f = 0 。
4. 若 **f = Infinite**，即传入了 无穷值，则抛出 RangeError 异常。
5. 若 **f < 0 或 f > 100**，即传入了不在 0 - 100 之间的值，则抛出 RangeError 异常。
6. 若 x = Infinite，即想要对 非准确值 保留位操作，则返回其 字符串形式。 例如，Infinity.toFixed(2) = 'Infinity'、NaN.toFixed(2) = 'NaN' 。
7. 让 x = 计算机所能表示的数学值 ℝ(x) 从 数字 或 BigInt x 到 数学值 的转换表示为 **x 的数学值**，或 ℝ（x）
8. 让 **返回值符号 s = ''**，即为符号定义 初始值 。
9. 若 **x < 0**，则将 **s = '-'**，并将 x = -x 。
10. 若 **x ≥ 10^21**，则 返回值 m = x 对应的科学计数法 表示的 字符串。
11. 若 **x < 10^21**，则 a. 让 **n = 一个整数**，其中 n / 10^f - x 尽可能接近于 **0**，如果有两个这样的 n，选择 较大的 n 。 b. 若 **n = 整数 0**，则 m = "0"，否则，m = 由 n 的 十进制 表示形式的数字组成的 字符串值（按顺序，不带前导零）。 c. 若 **指数 f ≠ 0**，则 **k = m.length 。**1. 若 k ≤ f，则 - z = 由代码单元 0x0030（DIGIT ZERO） 的 f+1-k 次出现组成的 字符串- m = z + m- **k = f + 1**2. 让 a = m 的第一个 k-f 码单元3. 让 b = m 的其它 f 个编码单元4. 将 m = a + "." + b
12. 返回 s + m 组成的字符串

**示例一： (1.125).toFixed(2) = 1.13 **

• 根据上述规范初始 x = 1.125，f = 2，s = ''
• 根据规范 7 可知 x = 1.125.toPrecision(53) = 1.125

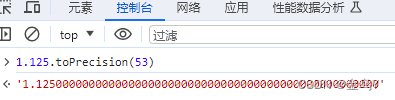
• 根据规范 11.a 提供的公式：**n / 10^f - x ≈ 0** 代入计算：**n ≈ 112.5**： - 此时最接近 n 的 整数 有 两个 值为 112 和 113，按标准取最大的 113- 在按 11.c 的规范得到 m = 1.13
• 最终返回 s + m= 1.13

**示例二： ** (-1.105).toFixed(2) = -1.10

• 根据上述规范初始 x = 1.105，f = 2，s = '-'
• 根据规范 7 可知 **x = (-1.105).toPrecision(53) = 1.10499... **
• 根据规范 11.a 提供的公式：**n / 10^f - x ≈ 0** 代入计算：**n ≈ 110.4...**： - 此时最接近 n 的 整数 只有 一个 值为 **110**（因为只有小数点后为 5 时，向上 / 向下 取整才会有两种情况）- 在按 11.c 的规范得到 m = 1.10
• 最终返回 s + m= -1.13

解决办法

以下是一些常见的解决方法：

1. 使用整数进行计算（先放大再缩小）： 既然我们遇到小数计算时才会出现误差，那么我们完全可以先把小数变整数计算之后再变成小数，这样就不会存在精度的问题。尽可能地将浮点数转换为整数进行计算。 例如，通过将小数位数乘以一个固定的倍数，将浮点数转换为整数，进行计算后再将结果转换回浮点数。这可以减少浮点数计算中的精度问题。 以 0.1 + 0.2 = 0.30000000000000004 举个例子，如下：1. 原式：0.1 + 0.2 = x2. 扩大 100 倍：0.1 * 100 + 0.2 * 100 = 100 * x3. 变式：100 * x = 34. 结果：x = 0.3 let num1 = 0.1,num2 = 0.2;console.log((num1*100+num2*100)/100); //0.3此方法局限就在于需要知道计算数字是几位小数。 且不是所有的浮点数都刚好被转成整数，例如：(44.8976).toPrecision(53) 取精度后的结果小数点后四位和实际值有误差，导致最后乘积的结果也是非正确值。
2. 使用专门的库或工具： 在处理需要高精度计算的场景中，可以使用一些专门的库或工具。例如，JavaScript 中的 Decimal.js、Big.js 或 BigNumber.js 等库提供了高精度的数学计算功能，可以避免精度丢失的问题。 需要的自行查阅： 1. math.js2. big.js3. bignumber.js4. decimal.js
3. 超过最值时，接口以 字符串 的形式返回对应的值： 前面提到的 后端返回 或 前端计算 产生的超过 安全范围的值，我们可以使用 BigInt 来处理，这是新增的原始值类型，它提供了一种方法来表示 大于 2^53 - 1 的整数。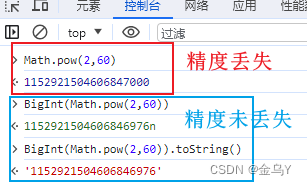 这里的 BigInt 不能用来处理后端返回超过安全范围内的值（如 id），因为当我们需要再将这些值转为 BigInt 之前就已经发生了精度丢失，所以在进行转换是无意义的。此时最好的方式就是让后端处理数据，使接口以 字符串 的形式返回对应的值。 当前端不得不临时转换为字符串时，可以这样处理： （1）正则替换： 如果我们使用的是axios请求数据，Axios 提供了自定义处理原始后端返回数据的 API：transformResponse , 可以这样处理： axios({ method: method, url: url, data: data, transformResponse: [function (data) { // 将Long类型数据转换为字符串 const convertedJsonString = data.replace(/"(\w+)":(\d{15,})/g, '"$1":"$2"'); return JSON.parse(convertedJsonString); }], })// 假设后端返回的JSON数据如下：const responseData = { id: 12345678901234567890, // 这是一个Long类型数据 name: "John Doe"};// 处理过的json数据console.log(responseData.id); // 这将输出字符串："12345678901234567890"console.log(typeof responseData.id); // 这将输出 "string" （2）json序列化处理 可以借助json-bigint这个第三方包来处理： json-bigint 中的 parse 方法会把超出 JS 安全整数范围的数字转为一个 BigNumber 类型的对象，对象数据是它内部的一个算法处理之后的，我们要做的就是在使用的时候转为字符串来使用。 通过启用storeAsString选项,可以快速将BigNumber转为字符串，代码如下： import JSONbig from "json-bigint"; axios({ method: method, url: url, data: data, transformResponse: [function (data) { + const JSONbigToString = JSONbig({ storeAsString: true });+ // 将Long类型数据转换为字符串+ return JSONbigToString.parse(data); }], }) // 假设后端返回的JSON数据如下： const responseData = { id: 12345678901234567890, // 这是一个Long类型数据 name: "John Doe" }; // 处理过的json数据 console.log(responseData.id); // 这将输出字符串："12345678901234567890" console.log(typeof responseData.id); // 这将输出 "string"
4. 避免直接比较浮点数： 由于精度问题，直接比较浮点数可能会导致不准确的结果。在需要比较浮点数的情况下，可以使用误差范围进行比较，而不是使用精确的相等性判断。
5. 限制小数位数： 对于一些特定的应用场景，可以限制浮点数的小数位数，以减少精度丢失的影响。例如，货币计算常常只保留到小数点后两位。
6. 使用适当的舍入策略： 在需要进行舍入的情况下，选择适当的舍入策略以满足实际需求。常见的舍入策略包括四舍五入、向上取整、向下取整等。 Number.prototype.toFixed=function (d) { var s=this+""; if(!d)d=0; if(s.indexOf(".")==-1)s+="."; s+=new Array(d+1).join("0"); if(new RegExp("^(-|\\+)?(\\d+(\\.\\d{0,"+(d+1)+"})?)\\d*$").test(s)){ var s="0"+RegExp.$2,pm=RegExp.$1,a=RegExp.$3.length,b=true; if(a==d+2){ a=s.match(/\d/g); if(parseInt(a[a.length-1])>4){ for(var i=a.length-2;i>=0;i--){ a[i]=parseInt(a[i])+1; if(a[i]==10){ a[i]=0; b=i!=1; }else break; } } s=a.join("").replace(new RegExp("(\\d+)(\\d{"+d+"})\\d$"),"$1.$2"); }if(b)s=s.substr(1); return (pm+s).replace(/\.$/,""); }return this+""; }
7. 注意数值范围： 在进行浮点数计算时，要注意数值的范围。超出浮点数表示范围的数值可能会导致精度丢失或溢出的问题。

参考文章：

线上紧急Bug：80%前端可能会遇到的数据精度问题

后端问为什么前端数值精度会丢失？ - 掘金

math.js是如何处理小数问题的 - 掘金

探寻 JavaScript 精度问题以及解决方案 - 掘金

【JS】关于精度丢失，产生的原因以及解决方案_js 加法丢失精度_swimxu的博客-CSDN博客