学习大模型开发之前,我们需要有足够的储备知识,类似于基础的python语法相信大家也都是十分熟悉了。所以笔者也是考虑了几天决定先给大家补充一些深度学习知识。
首先问大家一个问题,学习大模型之前为什么要先学习深度学习知识呢?
首先,深度学习是大模型的基础,理解其原理、结构和训练方法能够有效地指导大模型的设计和优化。同时,许多深度学习技术,如反向传播和优化算法,在大模型的训练中也至关重要,掌握这些技能可以提升处理复杂模型的能力。此外,大模型的实现往往依赖于深度学习框架,学习其基本操作有助于提高构建和调整模型的效率。深入掌握深度学习的核心概念还能加快实验和迭代开发的速度,而调试和优化的经验则为应对大模型提供了重要支持。总之,学习大模型开发之前,理解深度学习是必要的基础。
1. 深度学习简介
什么是深度学习? 首先深度学习是机器学习的一个分支,是通过模拟人脑的神经网络结构来进行模式识别和学习。他在语音识别、图像识别,NLP以及其他很多领域展现了前所未有的性能,其中大语言模型是其NLP领域的一大应用。
深度学习技术的核心技术在于深度神经网络,这种神经网络由多层的神经元组成,能够自动的从大量数据中学习复杂的表示,每一层都从前一层学习到的信息中提取到更高级的特征,这种层次化提取方法使得深度学习在处理大量非结构化数据(如图像、音频和文本)时表现出色。
深度学习的一个关键特点是其能力在很大程度上依赖于数据量和计算能力。随着数据集的不断增长和计算能力的显著提高, 深度学习模型能够学习到更复杂的数据表示, 解决以往算法难以
处理的问题。
在NLP 领域中,深度学习的应用表现尤为出色。大语言模型, 如OpenAI的GPT 系列、 Google的BERT等,都是基于深度学习技术构建的。这些模型能够理解、生成、翻译文本, 甚至完成复杂的推理任务。它们通过在海量的文本数据上训练, 学会了语言的深层语义和语法规则, 从而能够在各种 NLP 任务上达到或超过人类的表现。
深度学习为处理和理解人类语言开辟了新的可能性。与传统的基于规则的方法相比, 深度学习允许模型自动从数据中学习语言的复杂规律,而不需要人工设计特定的语言规则。这种从数据直接学习的能力,使得大语言模型能够灵活地应对各种语言变化和复杂的语言现象。
深度学习不仅推动了NLP技术的飞速发展,也为大语言模型的构建提供了理论基础和技术支持。了解深度学习的基本原理和应用是理解大语言模型的关键。随着技术的进步, 深度学习和大语言模型将在未来继续引领NLP 领域的创新和突破。
2. 深度学习基本原理
神经网络基于人脑的工作原理设计,用以处理复杂的数据模式。它们由相互连接的节点(或神经元)层组成,包括输入层、一个或多个隐藏层以及输出层。本部分将探讨神经网络的基本组成和工作原理。
每个神经元作用:每个神经元接收一组输入值,进行加权求和,然后通过一个激活函数进行非线性变换。
2.1 组成部分
(1) 输入层( Input Layer): 接收外部输入数据。
(2) 隐藏层( Hidden Layer ):负责处理数据的特征提取和转换, 可以有多个。
(3) 输出层( Output Layer):生成模型的预测结果。
每个神经元之间的连接都有一个权重( weight) 和偏置( bias), 它们是学习过程中调整的参数。
在后面我们会深入解析模型中的两个核心要素:权重和偏置。不仅将探讨它们在前向传播过程中的作用, 还将讨论激活函数、损失函数、反向传播及优化算法等关键机制, 以全面理解这些概念如何共同作用于神经网络的学习过程。
2.2 权重和偏置
(1)权重:确定前一个神经元的输出对当前神经元的影响程度。
(2)偏置:为每个神经元输出添加一个固定偏移量, 增加网络的灵活性和非线性表达能力。
2.3 前向传播
数据通过网络从输入层流向输出层,这一过程称为前向传播。每个神经元的输出由加权输入的总和加上偏置之后的结果, 经过激活函数处理后得到。激活函数的引入是为了提高网络处理非线性问题的能力。
2.4 激活函数
激活函数决定了神经元是否应该被激活,它为神经网络提供了非线性处理能力。常见的激活函数有以下几种:
** Sigmoid**:常用于二分类,但在深度网络中容易导致梯度消失。
** Tanh**:与Sigmoid类似,输出范围在-1到1之间,通常比Sigmoid更好。
** ReLU (Rectified Linear Unit)**:在深度学习中广泛使用,输出为输入值与0中的较大者,避免了梯度消失问题。
** Softmax**:用于多类分类问题的输出层,将输出转化为概率分布。
在下面我们会更详细的讲解这几种激活函数。
2.5 损失函数和反向传播
神经网络的训练目的是最小化预测值和实际值之间的差异,这通过损失函数(如均方误差或交叉熵)来衡量。训练过程中, 利用反向传播算法根据损失函数的梯度调整权重和偏置,从而优化模型的性能。
梯度是指损失函数关于模型参数(权重和偏置)的导数。它描述了当模型参数发生微小变化时, 损失函数值的变化率。梯度指向的方向是增加损失函数值的方向, 而梯度的反方向则是减少损失函数值的方向。因此,在优化过程中, 应沿着梯度的反方向调整参数, 以期望减少损失函数的值, 即减少预测值和实际值之间的差异。
2.6 优化算法
优化算法(如SGD、 Adam)用于更新神经网络中的权重和偏置, 目的是在损失函数的指导下找到参数的最优解, 以提高模型的预测准确性。
神经网络通过前向传播将输入信息转化为输出预测,然后通过反向传播和优化算法根据损失函数调整网络参数, 使得预测输出更接近真实标签。这个过程在训练数据集上重复进行,直到模型性能达到满意的水平。理解这些基本概念对于深入学习深度学习领域和开发高效的大模型而言至关重要。
层次结构
神经网络的层次结构是构建复杂模式和数据表示的基础,这种层次结构允许网络从简单到复杂逐渐抽象化数据的特征,从而学习到数据的深层次表示。下面是神经网络中的主要层次结构及其功能介绍。
3.1 输入层
神经网络的第一层,负责接收原始数据输入。输入层的神经元数量通常与数据特征的维度相匹配。例如, 对于手写数字识别任务, 如果输入图像的大小是28×28像素, 则输入层就会有784个神经元, 每一个神经元对应图像中的一个像素点。
3.2 隐藏层
位于输入层和输出层之间的层。由一层或多层隐藏层构成了网络的“深度”。每一层隐藏层通过权重和激活函数对输入数据进行转换和特征提取,随着层级的增加, 其能够捕捉更高层次的抽象特征。隐藏层的设计(如层数、每层的神经元数量、激活函数类型) 对网络的性能有重要影响。
3.3 输出层
神经网络的最后一层,负责输出最终的预测结果。输出层的设计取决于特定的任务目标, 如回归任务(指的是使用神经网络模型预测一个或者多个连续值得输出,例如房价预测)、二分类或多分类任务,它们分别可能使用线性、 Sigmoid或 Softmax激活函数。
3.4 层次结构的作用
随着数据从输入层通过隐藏层传递,每一层都在提取更高级别的特征。在图像处理任务中,较低层可能学习到边缘和纹理等基本特征,而较高层则能够识别出更复杂的形状和对象。
通过在每一层使用激活函数,神经网络能够捕捉输入数据中的非线性关系, 这对于解决复杂的问题至关重要。
在训练过程中, 通过反向传播算法, 每一层的权重都会根据损失函数的梯度进行调整以最小化预测错误。
网络的层次结构(即深度和宽度) 需要根据特定任务和数据集的复杂性来选择。过深的网络可能会导致过拟合和训练困难,而过浅的网络可能会无法捕捉足够的特征。实践中, 网络架构的设计和优化通常需要通过多次实验来确定最佳配置。
过拟合是指模型在训练数据上学到了过多的细节和噪声, 导致其在新的、未见过的数据上表现不佳, 失去了泛化能力。
神经网络的层次结构赋予了它处理、学习和表示复杂数据模式的能力, 是实现深度学习的基础。
一个简单的神经网络示例
本小节将使用 Python 和 TensorFlow库来构建一个简单的神经网络, 并解释每个部分的作用。该网络将包含输入层、一个隐藏层和输出层。
(1)导入必需的库。
# (1) 导入必需的库
import tensorflow as tf
from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential
(2) 构建神经网络模型。
# (2) 构建神经网络模型
# 初始化一个Sequential模型
model = Sequential()
# 添加输入层和隐藏层
# 注意:这里假设我们有3个特征,隐藏层有5个神经元,使用ReLU激活函数
model.add(Dense(5, input_shape=(3,), activation='relu', name='hidden_layer'))
# 添加输出层
# 注意:输出层使用sigmoid激活函数,适用于二元分类问题
model.add(Dense(1, activation='sigmoid', name='output_layer'))
# 编译模型,使用二元交叉熵作为损失函数,adam作为优化器,准确率作为评估指标
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# 打印模型概述
model.summary()
运行结果如下:
D:\ana\envs\sd\python.exe D:\pythoncode\sd\main.py
2024-08-10 16:46:10.474077: I tensorflow/core/platform/cpu_feature_guard.cc:193] This TensorFlow binary is optimized with oneAPI Deep Neural Network Library (oneDNN) to use the following CPU instructions in performance-critical operations: AVX2
To enable them in other operations, rebuild TensorFlow with the appropriate compiler flags.
2024-08-10 16:46:10.475594: I tensorflow/core/common_runtime/process_util.cc:146] Creating new thread pool with default inter op setting: 2. Tune using inter_op_parallelism_threads for best performance.
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
hidden_layer (Dense) (None, 5) 20
output_layer (Dense) (None, 1) 6
=================================================================
Total params: 26
Trainable params: 26
Non-trainable params: 0
_________________________________________________________________
进程已结束,退出代码为 0
这段代码解释如下:
(1) 神经元( Neurons):神经元是构成神经网络的基本单元。在Dense()层中,第一个参数定义了层中神经元的数量。例如, Dense(5,…)表示这个层有5个神经元。
(2)层( Layers):
①输入层:通过 input _ shape 参数在第一个 Dense 层定义。 input _ shape=(3,)意味着输入数据有3个特征。
②隐藏层: Dense(5, input _ shape=(3,), activation=' relu', name=' hidden _ layer')。该层是网络的隐藏层, 有5个神经元, 并使用ReLU激活函数。
③输出层: Dense(1, activation=' sigmoid', name=' output _ layer')。该层是网络的输出层, 只有一个神经元, 使用 sigmoid激活函数,适用于二分类问题。
(3) 权重和偏置( Weights and Biases):
它是神经网络在训练过程中学习的参数。在 TensorFlow中,这些参数是在 Dense()层创建时自动初始化的, 并在训练过程中通过反向传播算法进行更新。
(4) 激活函数( Activation Functions):
activation=' relu': ReLU 激活函数用于隐藏层。它帮助网络捕捉非线性关系。
activation=' signoid': Sigmoid激活函数用于输出层。它将输出转换为0和1之间的值, 适用于二分类问题。
(5) 查看模型摘要:
通过 model. summary(), 用户可以看到模型的结构,包括每层的输出维度和参数数量。
模型摘要展示了一个简单的 sequential模型, 它包含两层,分别为隐藏层和输出层。模型的总参数数量为26个, 占用空间大约为104字节, 所有参数都是可训练的。
输入层是指提供给第一个隐藏层作为输入的数据层, 相当于在隐藏层中定义的输入部分。
这个简单的示例说明了神经网络的基本组成部分, 这能帮助用户更好地理解每个部分的作用和含义。
5. 神经元
神经元是构成神经网络的基本单元,它是受生物神经元的启发设计的。一个神经网络由许多神经元相互连接组成,共同执行复杂的计算任务。这里将探讨神经元的基本组成部分:输入、结构和输出, 以及它们是如何一起工作的。
神经元的输入通常来源于外部数据或网络中其他神经元的输出。在最简单的形式中,每个神经元可以接收多个输入信号, 这些输入信号通过连接(称为突触)传入。在数学模型中, 每个输入都会乘以一个权重, 这个权重代表输入信号的重要性。输入信号经过权重调整后,会被累加起来, 形成神经元的总输入。
神经元的核心结构包括权重、偏置项和激活函数。权重决定了输入信号对输出的影响程度,偏置项则是一个常数, 多用于调整激活函数的激活阈值。累加的输入信号和偏置项的和将被送入激活函数。
激活函数是神经元的非线性转换部分,它决定了神经元是否被激活以及以多大强度输出信号。
为了更好地理解神经元的工作原理, 可以通过上面得简单示例来说明神经元的输入、结构和输出。
(1)输入:这个神经网络的输入层接收3个特征的输入数据。每个特征都是神经元的一个输入点。
(2)结构:
权重:每个输入特征都通过一个权重参数进行加权。权重代表了特征对于神经元激活的重要性。
偏置:除了加权的输入特征外, 每个神经元还加上一个偏置参数。偏置允许神经元即使在所有输入都是0时也有可能被激活。
激活函数:加权求和的结果和偏置之和通过激活函数进行非线性转换。隐藏层使用ReLU 激活函数, 它输出输入的正部分;输出层使用 Sigmoid激活函数, 它将输入压缩到0和1之间,适合于二分类问题。
(3)输出:
隐藏层的输出:隐藏层中的每个神经元通过ReLU激活函数处理其加权输入和偏置的和,产生的输出传递到下一层。
输出层的输出:输出层只有一个神经元, 它汇总来自隐藏层的信息, 并通过 Sigmoid函数输出一个介于0到1之间的值, 代表了某个类别的预测概率。
下面结合数学公式来理解其工作原理。神经元的基本操作可以概括为接收输入, 对输入进行加权求和, 加上偏置,然后通过激活函数产生输出。这个过程用以下公式表示。
![\ output=f[ \sum \limits _{i=1}^{n}(w_{i} \cdot x_{i})+b]](https://latex.csdn.net/eq?%5C%20output%3Df%5B%20%5Csum%20%5Climits%20_%7Bi%3D1%7D%5E%7Bn%7D%28w_%7Bi%7D%20%5Ccdot%20x_%7Bi%7D%29+b%5D)
其中, 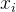是输入值, 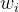是对应输入的权重, b是偏置项, f是激活函数, output 是神经元的输出。
对比前面的示例, 有一个输入层, 接收3个特征的输入数据;然后是一个隐藏层, 包含5个神经元, 使用ReLU 激活函数;最后是一个输出层, 包含1个神经元, 使用 Sigmoid激活函数。
●权重和偏置:每个输入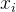都乘以相应的权重 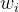,所有这些乘积的和加上偏置b。权重控制着输入信号的强度,而偏置允许激活函数沿输入轴移动, 为模型提供更多的灵活性。
●激活函数:对于隐藏层的神经元, 使用ReLU激活函数:f(x)= max(0,x)。ReLU 函数对于正输入返回输入本身, 对于负输入返回0。
对于输出层的神经元, 使用 Sigmoid 激活函数:。 Sigmoid函数将任意实值压缩到(0, 1)区间内, 使其可以解释为概率, 适合二分类问题。
神经网络中每个神经元的作用是接收输入,通过其内部的权重和偏置对这些输入进行加工,然后通过激活函数输出一个新的信号。这种结构使得神经网络能够学习复杂的非线性关系。
权重和偏置
在深度学习中, 权重和偏置是构建神经网络的基础元素, 它们决定了网络如何从输入到输出进行数据的转换。下面将探讨权重和偏置的作用,还有它们如何在神经网络中被优化以学习数据的复杂模式。 权重是连接神经网络中各个神经元的参数,它们代表了神经元之间连接的强度。在进行前向传播时, 输入数据会乘以相应的权重,这一过程是神经网络学习的关键。权重决定了输入信号对神经元激活程度的影响, 它有效地控制了信息的流向。 偏置是加在加权输入和之后的一个额外参数,它被视为每个神经元的可调节门槛。即使所有输入都是零, 偏置也允许神经元有非零的输出。偏置参数使神经网络模型更加灵活, 能够更好地适应数据。 加权输入和是指将输入数据与相应的权重相乘后的结果之和。 在训练过程中, 神经网络是通过调整权重和偏置来最小化损失函数, 这个过程称为反向传播。损失函数计算了神经网络的预测值与实际值之间的差异。通过梯度下降或其他优化算法, 由多层神经元组成的神经网络逐渐学习到一组使损失函数值最小化的权重和偏置,从而能够对未见过的数据进行准确预测。 下面以一个简单的线性模型进行说明,其输出y可以表示为输入x的加权和, 加上偏置b: y=w·x+b 其中, w代表权重, x代表输入, b代表偏置。在多层神经网络中,该公式会被多次应用, 每层的输出作为下一层的输入,通过非线性激活函数转换, 使得模型能够学习和表示更复杂的函数关系。 通过对大量数据的学习, 权重和偏置的调整使得神经网络能够捕获输入数据的内在规律,实现从简单到复杂的各种功能,从而完成分类、回归等多种机器学习任务。 权重和偏置是神经网络学习的基础,它们的优化直接关系到模型的性能和泛化能力。
激活函数
激活函数在神经网络中决定了一个神经元是否应该被激活,即是否对输入的信息做出响应。激活函数的引入是为了增加神经网络处理非线性问题的能力, 因为实际世界中的数据往往是非线性的。 如果没有激活函数,无论神经网络有多少层, 输出始终是输入的线性组合, 这限制了网络的表达能力。通过引入非线性激活函数, 神经网络可以学习和模拟任何复杂的非线性关系, 从而能够处理各种复杂的数据模式。 线性函数的图形表现为一条直线,而非线性激活函数的图形则不呈直线形态。当这些非线性激活函数应用于线性函数之上时, 它们为原本线性的输出赋予了非线性特性。 常见的激活函数如下: (1) Sigmoid函数, 其公式如下:  它的输出范围在0和1之间,这使得其特别适合用于表示概率或进行二分类问题中的决策。 Sigmoid函数的图形是一个S形曲线。经常用于二分类问题的输出层, 因为其输出可以被解释为属于某类的概率。由于在输入值很大或很小时梯度接近于零, 可能导致梯度消失问题, 限制了其在深层网络中的应用。 梯度消失是指在深层神经网络中,由于使用了某些激活函数(如Sigmoid), 在反向传播过程中, 由于输入值过大或过小, 梯度(导数)趋近于零, 导致深层网络中的权重更新变得非常缓慢或停止。 (2) ReLU 函数( Rectified Linear Unit), 其公式如下: f(x)= max(0,x) 对于正输入, 直接输出该值;对于负输入, 则输出为0。ReLU的简单性质使得其计算效率很高, 并且在正区间内不饱和,有助于缓解梯度消失问题。这在实践中非常受欢迎, 尤其是在隐藏层中。由于非饱和特性, ReLU 能够加速神经网络的训练过程。ReLU的一个缺点是“死亡ReLU”问题, 即部分神经元可能永远不会被激活, 导致相应参数不再更新。 (3) Tanh 函数( Hyperbolic Tangent), 其公式如下:  它将输入压缩到-1和1之间, 输出范围比 Sigmoid宽, 这有助于数据的规范化。与 Sigmoid相似, Tanh函数也是S形曲线, 但是它关于原点对称。 Tanh 函数经常用于隐藏层,因为它的均值为0, 这有助于数据在训练过程中保持稳定。与Sigmoid函数类似, Tanh函数在输入值的绝对值较大时也会出现梯度消失问题。 (4) Softmax函数, 其公式如下:  Softmax函数将一个实数向量转换为概率分布,每个数都被映射到(0,1)范围内, 并且所有输出值的和为1。 Softmax函数经常用于多分类问题的输出层。它的输出可以被解释为输入属于每个类别的概率, 从而进行分类决策。 Softmax是处理多类别直接互斥问题的理想选择, 如一个图像不可能同时属于多个类别。

Sigmoid、ReLU 和 Tanh 三个常见激活函数的图形

Softmax激活函数图
Softmax函数的输出图形是基于所有输入值的, 它将多个输入处理为一个输出概率分布。
选择哪种激活函数取决于具体的任务和网络的具体层。例如, ReLU 因其简单高效通常被用于隐藏层; Sigmoid因其输出范围是(0,1),多适用于二分类问题的输出层; Softmax多用于多分类问题的输出层。
版权归原作者 人生百态,人生如梦 所有, 如有侵权,请联系我们删除。