【一起学数据结构与算法】一招教你学会BF算法和KMP算法

目录

前言

这篇文章是小编对BF算法和KMP算法学习的整理，可能不太严谨，希望大佬勿喷，若有不足，多多指教！评论区见！

一、BF算法

1.1 思路：

思路就是主串中的元素与子串中的元素一一进行比较，匹配失败之后就让子串返回到0下标，主串回溯到开始匹配的下一位。
如果主串的长度为M，子串的长度为N，BF算法的时间复杂度为O(M*N)

有一个主串str和一个子串sub，现在要查找sub在str中的位置，怎么查找呢？
使用BF算法的思路，现在主串str匹配到 i 位置，子串sub匹配到 j 位置，则就有：

1. 如果当前字符匹配成功的(str[i] == sub[j])，则i++，j++，继续匹配下一个字符；
2. 如果匹配失败(即str[i] != sub[j])，令i = i - (j - 1),j = 0;相当于每次匹配失败后，i回溯，j被置为0.

比如举个例子：
主串：ABABABC???
子串：ABABC

具体的步骤：

1. str[0]为A，sub[0]为A，匹配成功，执行第一条指令： 如果当前字符匹配成功的(str[i] == sub[j])，则i++，j++，继续匹配下一个字符；可得str[i]为str[1]，sub[j]为sub[1],即接下来str[1]跟sub[1]匹配 (i=1,j=1)
2. str[1]为B，sub[1]为B，匹配成功，执行第一条指令： 如果当前字符匹配成功的(str[i] == sub[j])，则i++，j++，继续匹配下一个字符；可得str[i]为str[2]，sub[j]为sub[2],即接下来str[1]跟sub[1]匹配 (i=2,j=2)
3. 以此类推，直到str[4]为A，sub为C，匹配不成功，执行第二条指令：如果匹配失败(即str[i] != sub[j])，令i = i - (j - 1),j = 0;相当于每次匹配失败后，i回溯，j被置为0.这样i = 4 - (4 - 1) = 1了，相当于i回到了str[1]位置，然后sub回到了sub[0]，重新进行匹配；
4. 匹配又不成功，又执行第二条指令：如果匹配失败(即str[i] != sub[j])，令i = i - (j - 1),j = 0;相当于每次匹配失败后，i回溯，j被置为0.这样i = 1 - (0 - 1) = 2了，相当于i回到了str[2]位置，然后sub回到了sub[0]，重新进行匹配；
5. 就像这样，一直匹配，直到 j > sub.length()之后就算出i - j

这样讲大家可能还是不是很懂，那么就通过图的方式来理解！(此图借鉴于别的博主)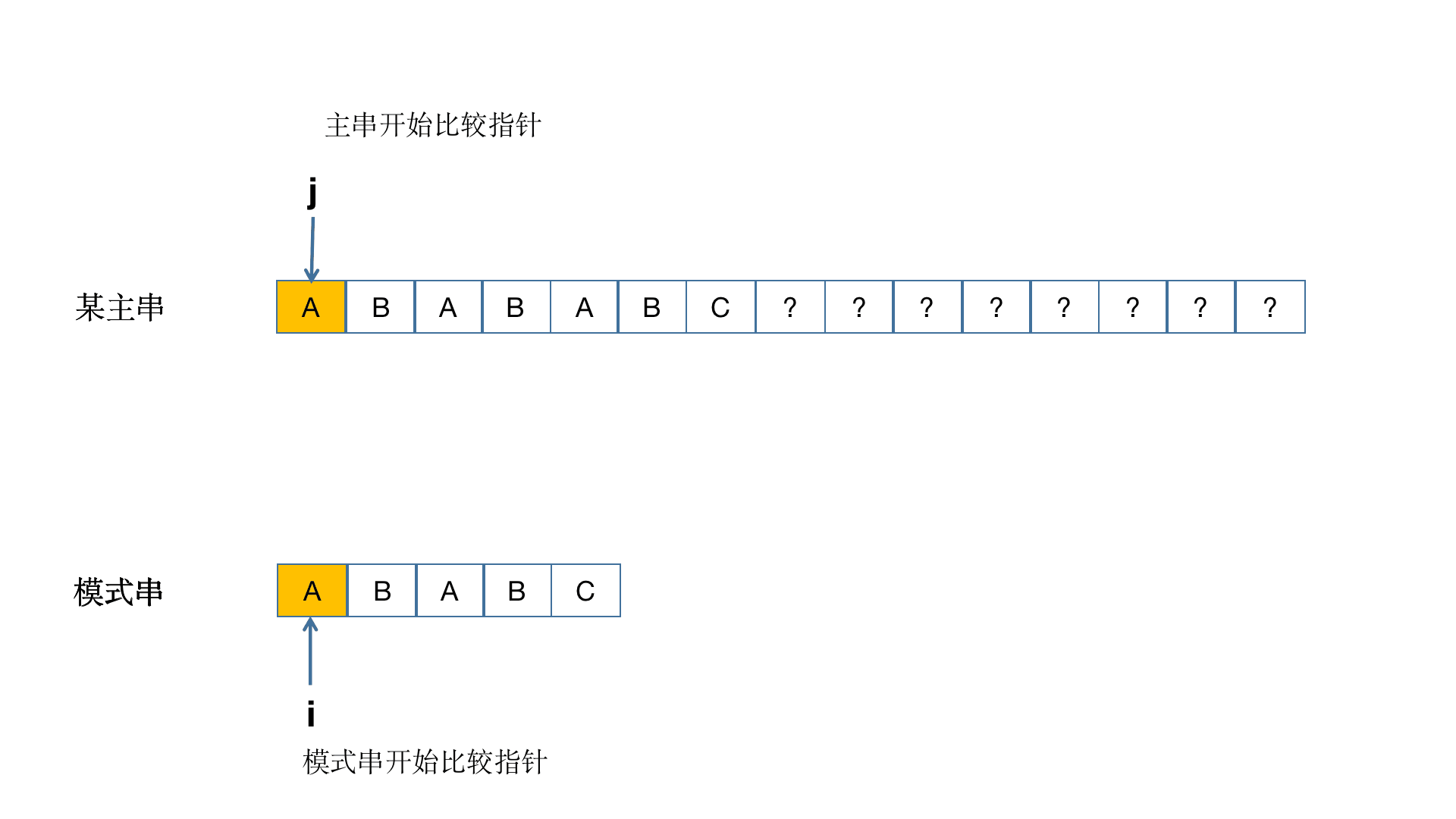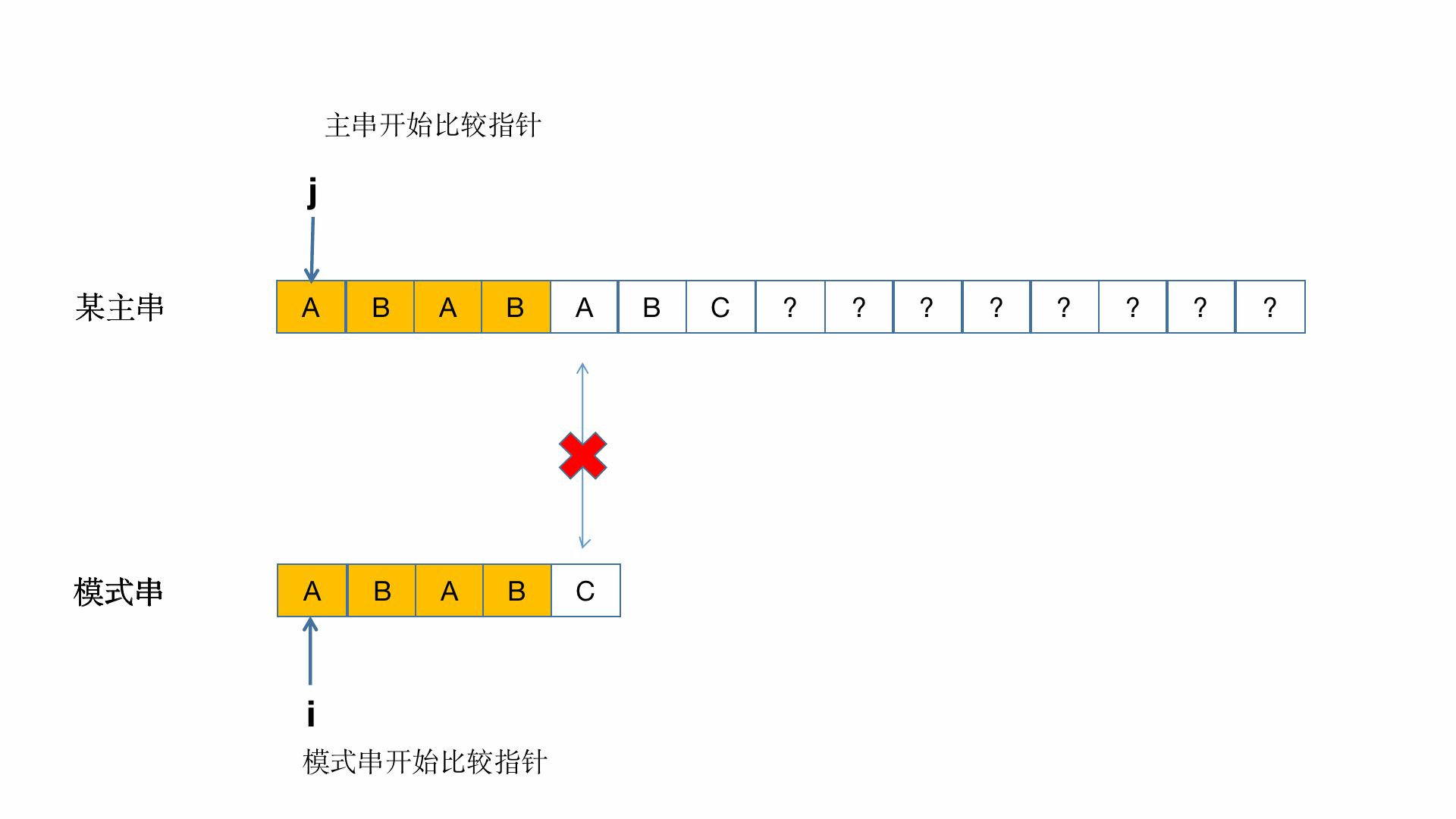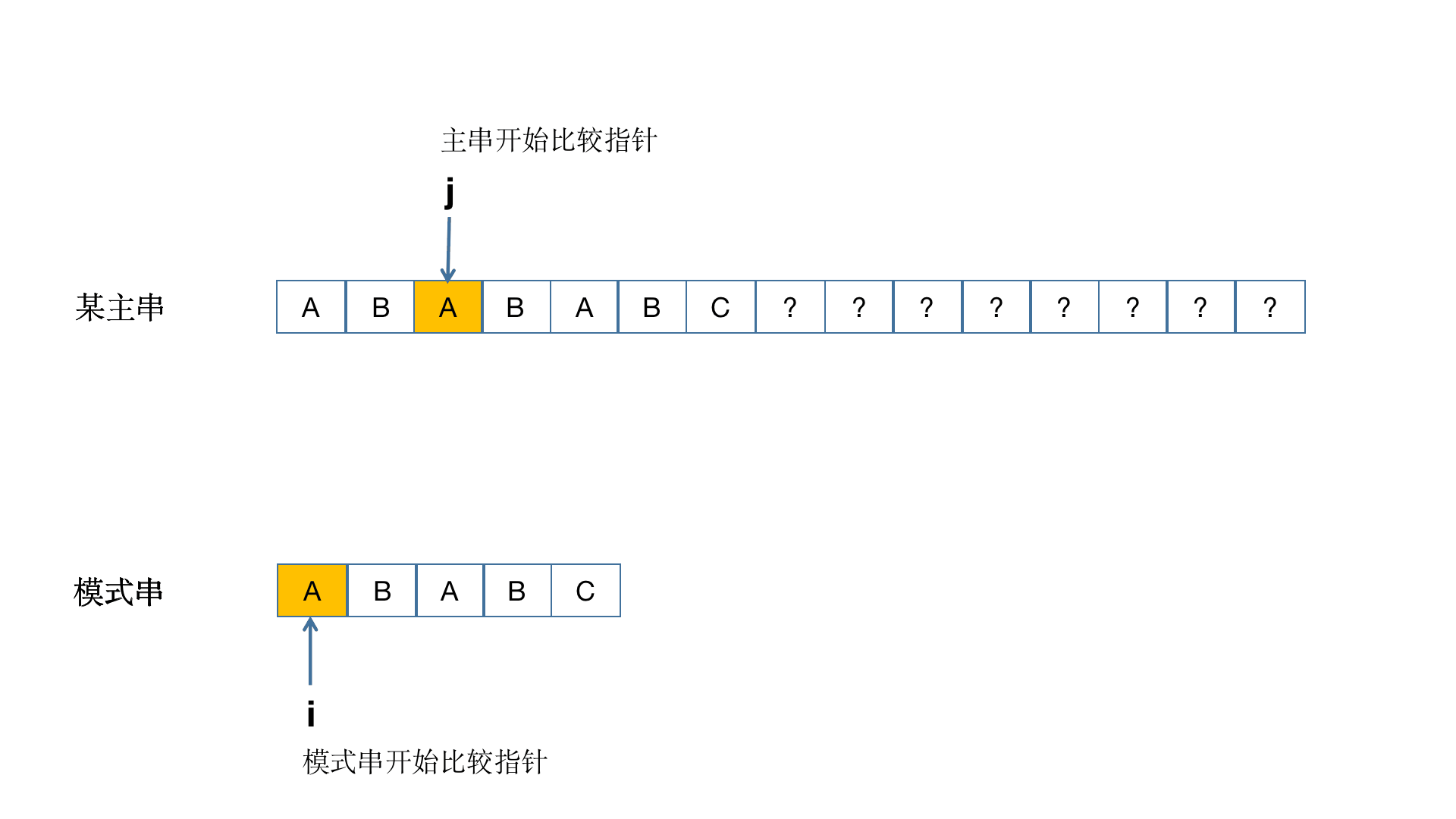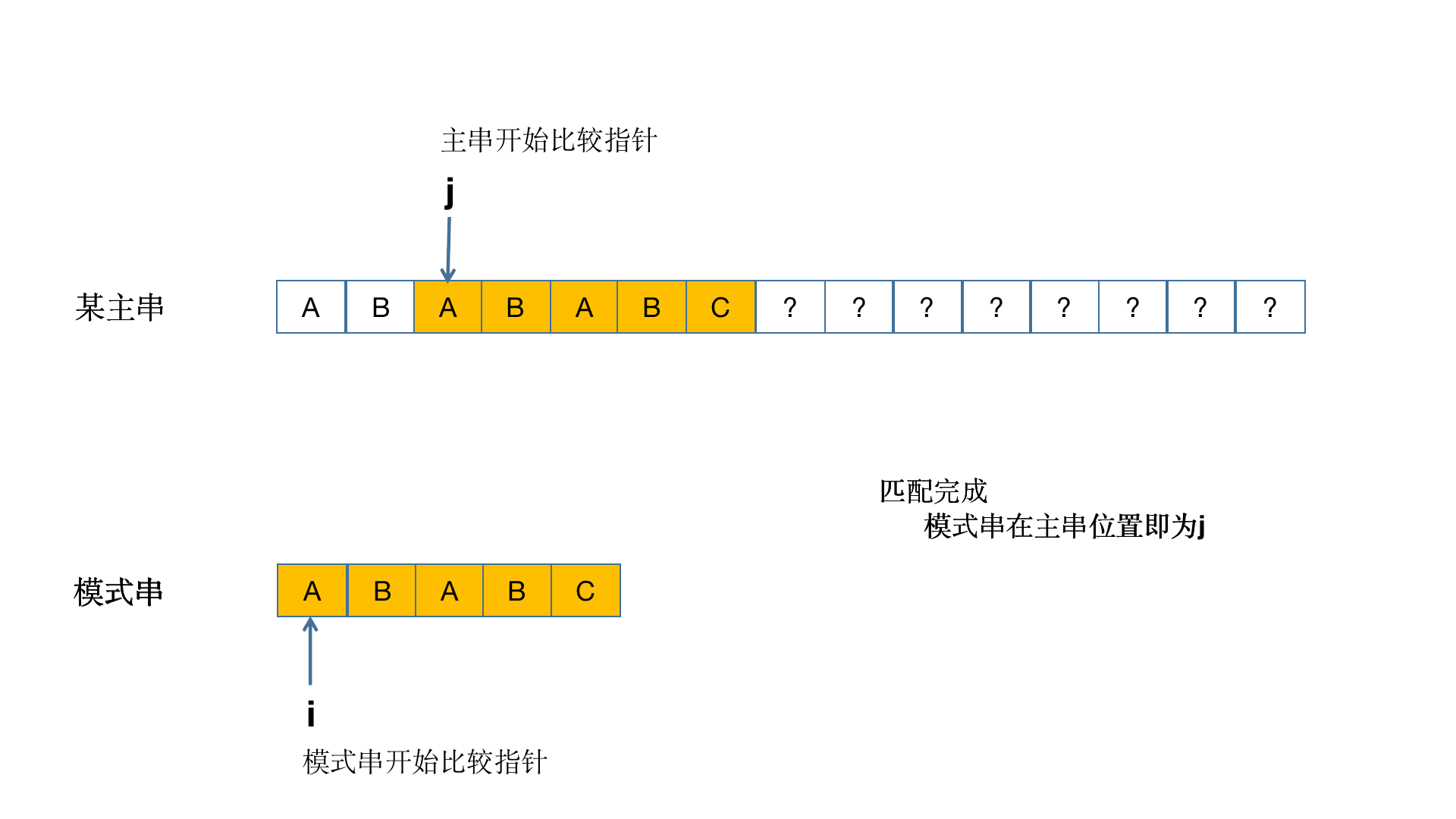

1.2 代码展示：

publicstaticint BF (String str,String sub){if(str ==null|| sub ==null){return-1;}int lenStr = str.length();int lenSub = sub.length();if(lenStr ==0|| lenSub ==0){return-1;}int i =0;//遍历主串int j =0;//遍历子串while(i < lenStr && j < lenSub){if(str.charAt(i)== sub.charAt(j)){
                i++;
                j++;}else{
                i = i - j +1;
                j =0;}}if(j >= lenSub){return i - j;}return-1;}

通过学习可以看出这种算法是一种暴力匹配算法，都知道这种方法虽然容易理解，但是不推荐去用！还需要再去优化一下！这样就有大佬就写出了KMP算法！

二、KMP算法 (Knuth-Morris-Pratt)

KMP算法的诞生：KMP算法是三位大牛：Knuth、Morris和Pratt同时发现的，于是取了他们名字的首字母然后组合起来，就成了该算法的命名。（来自百度）

2.1 思路：

kmp算法的思想是：
在主串中查找子串时，利用主串和子串中已经匹配的部分，跳过一些无用的比较，使主串的标记指针不会回溯，子串的标记指针移动。其实主要是子串中如果有部分内容和主串中一致，我们需要研究这些已知的匹配内容，这相当于我们需要研究子串，发现子串中存在的规律。
KMP算法的时间复杂度为 O(M+N)

假设现在主串str匹配到 i 位置，子串sub匹配到 j 位置

1. 如果j = -1，或者当前字符匹配成功（即str[i] == sub[j]），都令i++，j++，继续匹配下一个字符；
2. 如果j != -1，且当前字符匹配失败（即str[i] != sub[j]），则令 i 不变，j = next[j]。此举意味着失配时，子串sub相对于主串str向右移动了j - next [j] 位。

是不是把大家搞懵了？😜😜
给大家举个例子吧那就！

主串：abcababcabc
子串：abcabc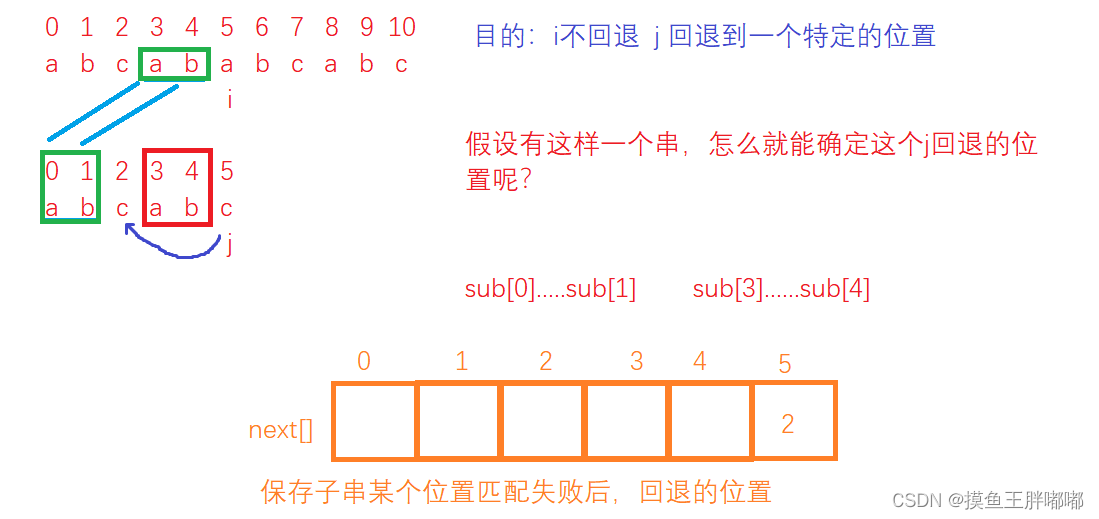

KMP的精髓就是next数组，那么应该怎样来求next数组呢？假定next[j]=k;

求k的规则：
找到匹配成功部分的两个相等的真子串（不包含本身）一个以下标0开始，另一个以j-1下标结束。
总有next[0]=-1,next[1]=0。
来两道练习吧！！

练习一： 举例对于”ababcabcdabcde“,求其的next数组？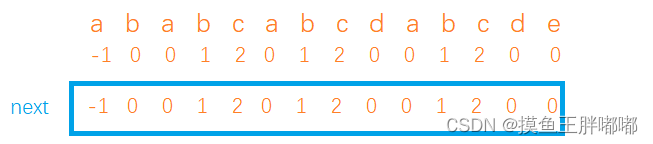

练习二： 举例对于”abcabcabcabcdabcde“,求其的next数组？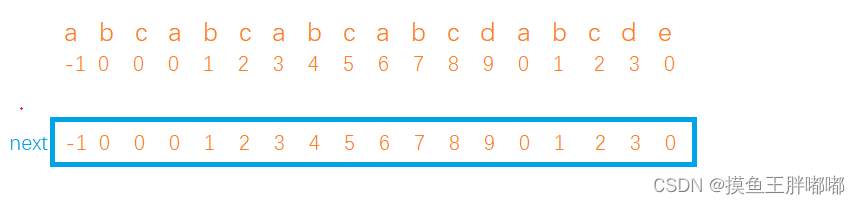

学会了去找next数组，接下来我们就可以去找一下规律了！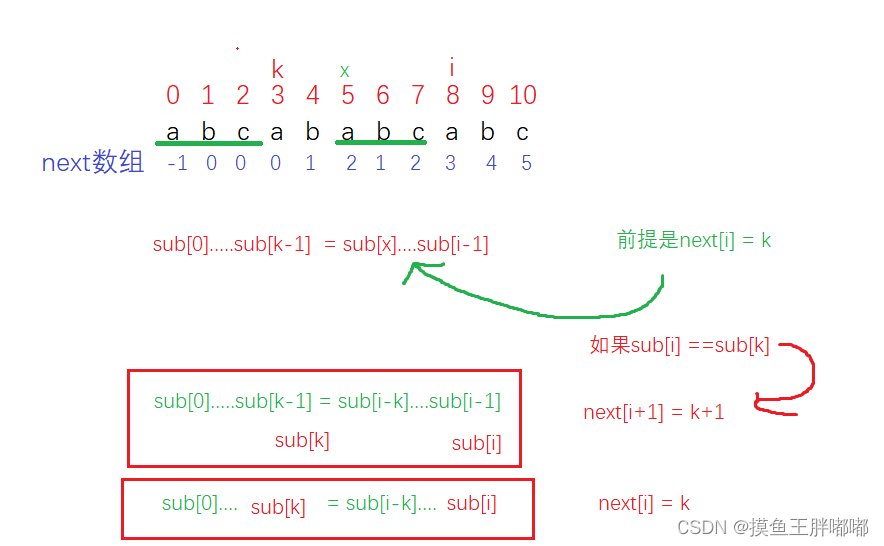

那么sub[i] != sub[k]会怎么样呢？
next[i+1] = ?

这里面有一个容易出错的点，当j==-1时也不要忘记了处理，当j==-1时说明回到了索引为0的位置，并且还没有找到与其匹配的项，就让j从索引为0开始与i一一比对。
基本的流程就是：

1. 寻找前缀后缀最长公共元素长度
2. 求next数组
3. 根据next数组进行匹配

整体匹配失败的过程：(同样是借鉴别的博主)

具体一次匹配失败匹配移动的过程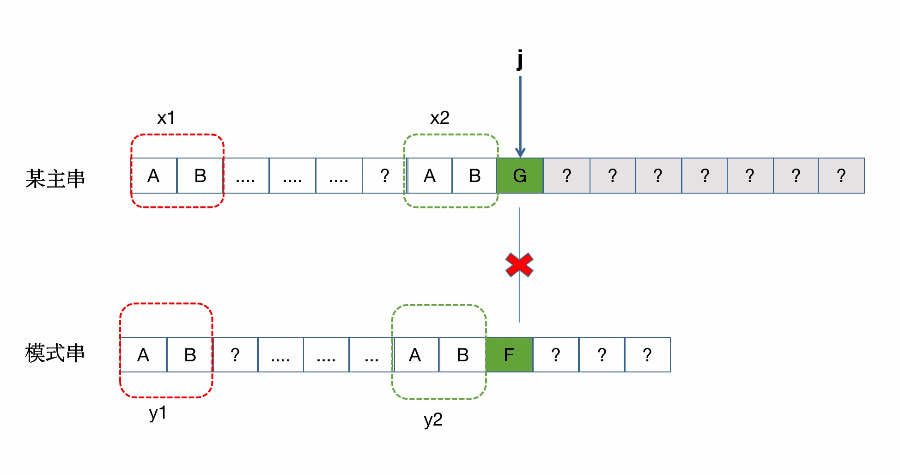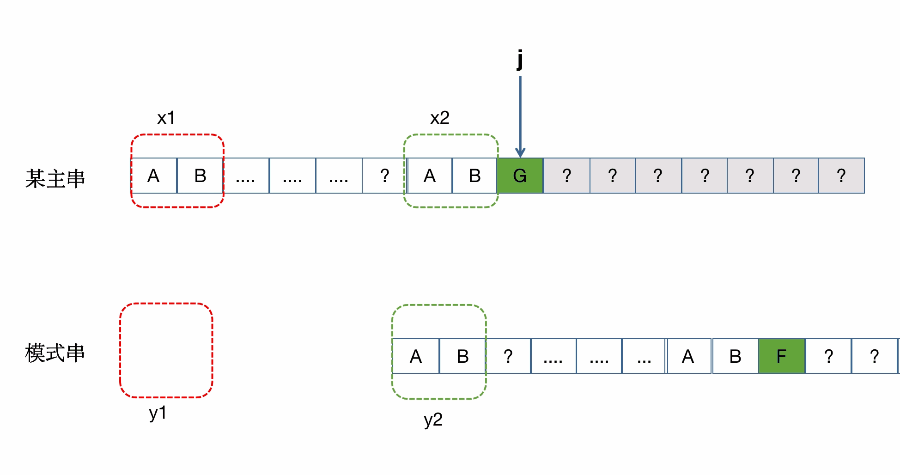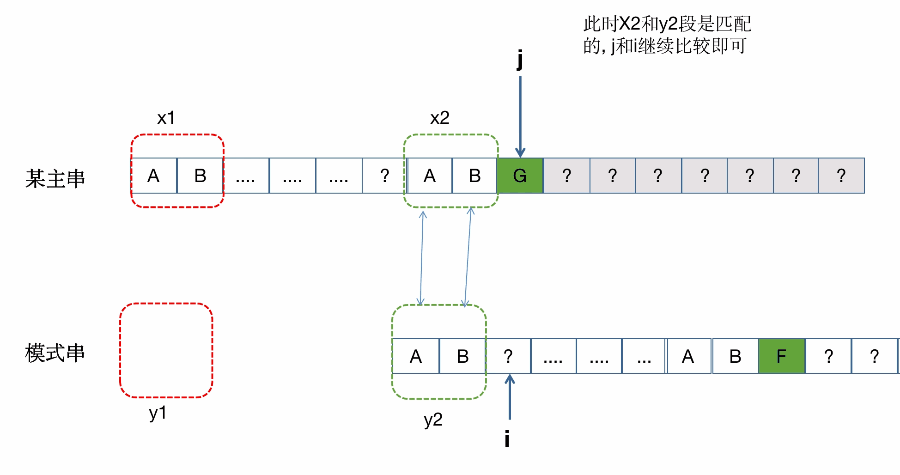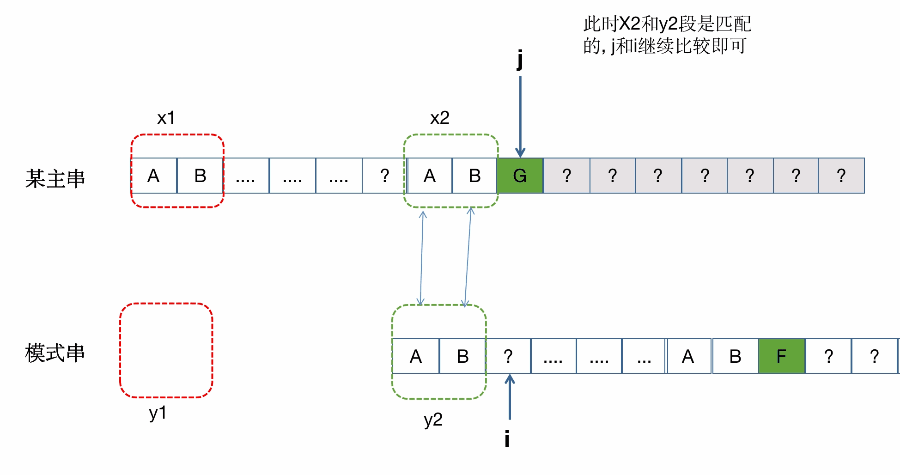

2.2 代码展示：

publicstaticint KMP (String str,String sub,int pos){if(str ==null|| sub ==null)return-1;int lenStr = str.length();int lenSub = sub.length();if(lenStr ==0|| lenSub ==0)return-1;if(pos <0|| pos >= lenStr)return-1;int[] next =newint[lenSub];//得到next数组getNext(sub, next);int i = pos;//遍历主串int j =0;//遍历子串while(i < lenStr && j < lenSub){if(j ==-1|| str.charAt(i)== sub.charAt(j)){
                i++;
                j++;}else{
                j = next[j];}}if(j >= lenSub){return i-j;}return-1;}publicstaticvoid getNext (String sub,int[] next){
        next[0]=-1;
        next[1]=0;int i =2;//提前走一步int k =0;//前一项的k//遍历子串for(; i < sub.length(); i++){//p[i] == p[k]if(k ==-1|| sub.charAt(i-1)== sub.charAt(k)){
                next[i]= k+1;
                k++;
                i++;}else{
              k = next[k];}}}

三、KMP算法的优化

如果有这样一个字符串：” a a a a a a a a a a g “
它的next数组：[-1,0,1,2,3,4,5,6,7,8,9]

假设在索引为9的位置匹配失败，则j会不断回退直到j==-1,这样效率就比较低了，有什么办法能够一步到位回退呢？
我们不妨优化一下next数组：为了区别，不妨将将优化后的数组取名为nextval

规则如下：

1. 如果回退到的位置和当前字符一样，就写回退那个位置的nextval值
2. 如果回退到的位置和当前字符不一样，就写当前原来的nextval值

练习串 t = ”abcaabbcabcaabdab“，该模式串的next数组的值为？nextval数组的值为？
next：[-1, 0, 0, 0, 1, 1, 2, 0, 0, 1, 2, 3, 4, 5, 6, 0,1]
nextval:[-1, 0, 0,-1, 1, 0, 2, 0,-1, 0, 0,-1, 1, 0, 6,-1,0]

publicstaticvoid getNextval (String sub,int[] nextval){int lenSub = sub.length();
        nextval[0]=-1;
        nextval[1]=0;int i =2;int k =0;while(i < lenSub){if(-1== k || sub.charAt(i-1)== sub.charAt(k)){
                nextval[i]= k +1;
                i++;
                k++;}else{
                k = nextval[k];}}
        i =2;while(i < lenSub){if(sub.charAt(i)== sub.charAt(nextval[i])){
                nextval[i]= nextval[nextval[i]];}
            i++;}}