模型可解释性——故障检测、识别和诊断
反事实推理是可解释性的一般范式。它是关于确定我们需要对输入数据应用哪些最小更改,以便分类模型将其分类到另一个类中。
一个典型的应用场景是故障检测和诊断。让我们想象一下,我们可以使用放置在整个生产链中(通常在每个工作站中)的传感器来精确监控制造过程。使用这些数据,我们可以在制造过程的每个阶段跟踪产品。因此,与最终出现故障的产品相关的数据可以被记录下来以用于进一步分析,以试图追溯引入故障的位置。尤其是,我们会对找到出现故障的工作站感兴趣,如果可能的话,我们会对诊断那里可能出错的地方(如果数据允许)感兴趣。在这一点上,您可能已经猜到,主要目标是在尝试发现问题所在时避免长时间停止生产链。拥有能够在眨眼间提供此类答案的人工智能可能会证明非常有用,而且最重要的是,这对业务有好处,这是一个足够好的借口,可以解决您将在阅读本文其余部分时遇到的所有理论困难文章。

好消息是我们能够设计非常有效的故障检测模型 (FDM)。后者能够实时分析来自异构性质(数字、分类……)的大量数据,并在生产的不同步骤进行测量,以预测给定的制造元件是否有故障。不太好的消息是,解释此类模型的决策以提供故障诊断要困难得多。常用的 FDM 通常是非常复杂的/黑匣子模型,除了透明之外的一切。
在这篇文章中,我们展示了一种称为树集成模型的模型类别,属于流行的高性能模型,例如 XGBoost、LightGBM、随机森林……,我们可以使用一种称为“反事实解释”的方法来解释决策这样的模型。为简单起见,我们在这里只考虑将数据分为两类的二元分类模型:正常/故障。
对于被模型分类为错误的给定查询点,我们计算一个称为反事实示例(以下称为 CF 示例)的虚拟点。后者是输入空间中欧几里得距离方面的最近点,被模型归类为法线。这一点是虚拟的,因为它不一定存在于训练集中。大多数时候它不会,我们根据 FDM 模型参数构建它。CF 示例背后的几何直觉如下图所示。

二类分类器的决策区域。模型预测类别 1 的区域标记为“C1”,模型预测类别 2 的区域标记为“C2”。点 P#i 的最接近的反事实示例由 CF#i 表示。它是最接近 P#i 的点,它被模型归为第 2 类。在上图中,我们将所有点 P#i 放在第 1 类中,因此我们在第 2 类中寻找它们各自的反事实示例。
对于错误数据,我们可以使用其关联的 CF 示例说明需要在最小值处更改哪些内容,以便它返回到正常类。你看到它在几英里外,这是我们用来进行故障诊断的。这种方法非常强大,因为它可以发现细微的变化,从而将错误数据与正常数据区分开来。这些变化可以是多变量的,因为与正常状态相比,几个输入特性可能已经发生了变化。(CF vs 特征重要性?)最重要的是,我们有与物理设备(工作站)和制造过程相关的输入特征。因此,如果错误输入数据与 CF 示例的比较发现要恢复正常,我需要将 25 号站的温度降低 0.1 °C,并将 31 号站的压力增加 0.05 ,我可以快速安排这个对我的生产链进行干预,以避免出现新的故障并浪费更多的时间/材料。而且,这就是反事实解释特别有趣的地方,它们让您准确了解纠正问题所需采取的最小行动。好吧,我希望我让你相信,手头有一个与错误数据相关联的 CF 示例是快速解决问题的关键,并且可能节省大量资金(认为一切都与金钱和时间有关,这是陈词滥调节省……)。
在这一部分中,我们展开了一种有效的算法方法,以在树集成模型的情况下计算与错误数据相关的最接近的 CF 示例。我会尽量保持整体相当直观,但有时我必须挖掘数学。敏感的读者可以跳过这些部分,它不妨碍整体的理解,您仍然可以保留它以备后用,当您完成生产链上的问题解决时,您有足够的空闲时间。
首先,我们需要输入树集成模型的特殊性。CF 示例是根据模型的特殊性(即模型参数)计算的,因此理解它们的工作原理似乎是一个相当重要的步骤。
让我们从决策树开始,它是此类模型的基本组件。更准确地说,二叉决策树:在这种树的每个节点中,我们通过将输入特征与单个阈值进行比较来分析输入特征的值。如果特征值高于阈值,我们转到右分支,否则,我们转到左分支。我们重复这个逻辑,直到我们最终得到与分数(对一个班级的投票)相关联的一片叶子。现在让我们从几何角度分析它的含义。我试图在下图的图表上表示它。

输入特征空间中的决策区域对应于决策树的叶子。这些区域是盒子/多维区间,在某些方面可能是打开的。输入空间是二维的。在节点Ni中,我们指出输入数据的哪个维度dj被分析,以及与哪个阈值ci进行比较。因此,节点Ni与一对(dj, ci)相关联。可以检查的是,即使在树的根和叶子之间的路径上对一个特征进行了两次以上的测试,只有两个测试有效地描述了与叶子相关的决策区域,其他测试都是冗余的。这个属性保存输入维度的数量。N1和F1之间的路径中包含一个特征d2冗余测试的例子:在节点N2中,我们测试“d2 < 2.5”,在节点N4中,我们测试“d2 < 1.4”,相当于只测试“d2 < 1.4”。
从几何上讲,决策树的叶子似乎是多维的盒子(可以在某些边打开)。为了在数学上更准确,我们可以说叶节点是多维区间。那么,树组合呢?您自己可能很容易得出结论,它不过是多维区间/框的集合,以及它们关联的类投票/分数。要预测输入元素,我们只需要弄清楚它属于哪些框(框可能彼此交叉),并计算相关的分数。从数学上讲,如果我们将树集成模型F表示为一对(B, S),其中B是盒/叶的集合,S是相关分数的集合,那么与F相关的预测函数即为:
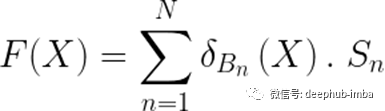
树集成模型预测功能。N为模型叶的个数。Bn表示第n个叶子,Sn表示与这个叶子相关的分数。Sn是一个K维向量,其中K是与分类问题相关的类的数量。它通常是一个稀疏向量,只投票给一个类(即只有一个非零系数)。为了知道与输入点X相关的模型的决策,我们计算“arg max(F(X))”。如果X属于叶片Bn,则δBn(X)=1,否则δBn(X)=0。
您可能会认为像XGBoost这样的模型可能会产生更复杂的决策函数,但实际上,不是这样的……对于二进制分类,它产生一个分数(在0到1之间),一旦与阈值(默认为0.5)比较,它就会告诉您数据属于哪个类。
此时,我们将尝试根据模型的决策区域的几何分解来确定CF示例。这就是事情变得棘手的地方,因为我们不能直接使用我上面提到的分解。下面的例子应该足以让你相信我们不能,世界比它看起来更糟糕。

几个叶子/框的交集会出现新区域,其得分是通过将相交形成这些区域的各个框的得分相加来确定的。例如,绿色区域的得分通过计算S1+S2+S3确定,红色区域的得分通过计算S1+S3确定。
在上图中,三个框 B1、B2 和 B3 的交集出现了两个新的决策区域(以红色和绿色突出显示)。我们无法确定这些区域属于哪个类别,除非我们将相交形成这些区域的框的分数相加。好吧,你猜怎么着?这就是我们所做的。我们对原始分解执行“超级分解”,以确定所有交叉区域和其他交叉区域。出于算法原因,我们计算了一个“超级分解”,它也是一个盒子的集合。所以,它看起来更像是这样:

三个相互交叉的盒子的初始集合的超级分解。超级分解也采用盒子集合的形式。后者不一定是能找到的最简单的类盒分解(就盒子的数量而言)。
问题的所有困难在于设计一种算法方法来计算一个类似盒子的超级分解,从而避开问题的潜在组合。实际上,以蛮力的方式表述,问题将等于确定,对于任何一组“k”个框,这些“k”个框是否形成最大的交叉区域,即它们的交叉区域是否不为空,并且如果有 “k”之外的其他盒子不考虑与该区域相交的盒子。这个问题是组合的,即使对于中等数量的盒子也难以处理。我们提出了一种逐维构建交集框的算法。我们使用边垂直于坐标轴的盒子的一个方便的属性:如果两个盒子根据一个特定的维度不相交,则它们根本不相交。下图说明了这个想法。
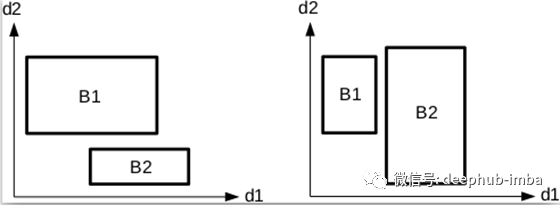
如果两个盒子根据某一特定维度不相交,则它们根本不相交。在左图中,两个框根据尺寸 d1 相交,但不根据尺寸 d2 相交。在右图中,两个框根据尺寸 d2 相交,但不根据尺寸 d1 相交。
这种特性产生了一种树状的分层探索结构。每一层对应输入空间的一个维度。在每个节点中,我们根据树状结构当前层级对应的维度计算存储在该节点中的框的最大交集。如果两个框不按照这个维度相交,它们将不再一起出现在树的另一层的同一个节点中,因为根据上面的属性,它们没有机会一起形成一个相交区域。
重新发挥我作为数字艺术创作者的惊人天赋,我尝试在下面以图形方式“运行”算法,达到了文字所能提供的限制,并且不想用硬核算法证明来扼杀你。该算法主要是关于前面提到的树状结构的构建。该结构在其叶子中包含由树集成模型的叶子形成的交叉区域的盒状超级分解。
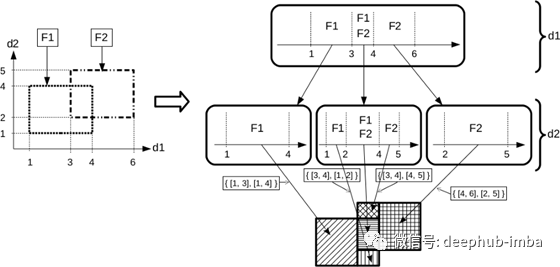
由框分解算法构建的树状探索结构。我们在这里考虑在二维特征空间中具有两个叶子的模型 (F1, F2)。该算法逐维进行。第一层对应维度d1,根据维度d1分解为模型叶的最大交叉区间。在这个级别之后,我们最终得到三个独立的叶子子集,我们对其应用相同的一维分解过程,但这次是根据维度 d2。阴影区域表示算法产生的最大交叉框。
在树状结构的每个节点中,我们总是解决相同的交集问题:给定一个框列表和与节点关联的输入空间的维度,我们寻找这个维度中框的最大交集,即 我们解决了前面提到的组合问题,但在一个维度上。因此,我们不再处理框,而是处理一维间隔,即所考虑维度中框的投影。幸运的是,在 1D 中,问题不再是组合问题,甚至在考虑的区间数量上变得线性。想法是将所有间隔放置在 1D 轴上,如下图所示。

从一维区间的集合中寻找一维中最大相交的区域(区间)。如果一个区域对应于 k 个区间的交集区域,则称该区域具有最大交集,其中 k 是在该区域相交的最大区间数。为了计算这些区域,我们将所有间隔放在一维轴上,并且在每次间隔开始或结束时创建一个新的最大交叉区域。在上面的例子中,从区间 {I1, I2, I3} 的集合中,我们提取了五个最大的交叉区域 Z1、Z2、Z3、Z4 和 Z5。
然后我们注意到,每次间隔开始或结束时都会开始一个新的最大交集一维区域(这是一个一维区间),除了最后一个区间结束,它终止了最后一个最大交集区域。因此,如果我们考虑 N 个区间的初始集合,我们将最多有 2.N-1 个最大交叉区域。在算法上,我们必须对所有放在一起的区间的开始和结束进行排序,这相当于对 2.N 个点进行排序。在实践中,这个操作可以在超级分解算法中跳过,通过在每个维度上分别对组成树集成模型的框进行预排序,并且通过观察使用掩码操作从有序集合中提取子集会产生一个有序子集.因此,我们可以考虑节点中框的子集,而不必根据与节点关联的维度再次对它们进行排序。因此,我们最终对树状结构的每个节点进行了处理,与问题的初始复杂性相比,这些处理的成本低得惊人。
在这一点上,你可能已经预料到,超级分解算法最终可能会产生如此多的决策区域,以至于它甚至不适合你的计算机的内存。这就是残酷的现实。因此,我们现在将寻找优化,它仍然允许找到确切的CF示例,但限制了实际构建的区域的数量。其主要思想是,我们不需要构建模型的整个决策区域,而只需围绕查询点构建一些内容,以便从其他类中找到示例。因此,我们希望限定CF示例所在的搜索区域的大小。作为第一次尝试,我们可以使用训练数据来做到这一点:给定一个查询点,我们在训练集中寻找被模型分类为正常的最近的数据(注意,我说的是“分类”而不是“标记”)。这为搜索区域的大小提供了第一个可靠的上界。使用此方法,我们将只建立位于此上限内的搜索区域。这很方便,因为用于构建决策区域的算法是逐维进行的。因此,对于给定的维数,如果部分构建的决策区域已经超过了上界,我们可以停止在搜索树的相应节点上的搜索。这种方法的通用名称是“分支绑定”,在需要沿着树状结构的分支执行探索的所有场景中特别有用(这显然就是我们的例子)。
我希望你还在跟着我进行这个危险的分支探险。还有许多其他实际的优化,最有效的是以深度优先的方式探索搜索结构。这为我们提供了一个比单独使用训练集计算的上界更好的快速上界。在实践中,我们使用多线程并行地维护了几个深度优先的探索,以保持它的有效性。每当我们发现一个比上一个更紧的上界时,我们就更新最紧上界的值,并将新的上界传递给所有线程,以便立即使用。这样就可以非常快速地对搜索树进行修剪,并且可以在一眨眼的时间内(有时还要多一点,这取决于你眨眼的速度)尽其所能地探索模型的决策区域。
最后一点,在某些时候,维度会对你有利(能写出这样的东西很罕见,所以我几乎可以说这是历史性的时刻,而且,如果我不打字,你会看到我的笔迹在颤抖)。简单地说,添加的维度越多,部分构建的框到查询点的距离超过上限的可能性就越大。这个简单的效果使您通过搜索树创建的区域数量趋于稳定,甚至有时在某个维数之后(略微)减少。好吧,不管怎样,我们都不要对这个问题过于热情,最好添加一些好的优化,并祈祷快速得到结果。
所以,现在我把筹资原则展开,让我们把双手放在代码中。我使用c++程序编码所有上面的优化(甚至更多),我用R(和也许我会写一个python包装器在未来的未来,所以它可以使用您最喜欢的高级编程语言)。我将在另一篇博客文章中向您展示如何进行漂亮而简单的Rcpp包装,以至于您可能会考虑放弃python。
R包可以在我的github上找到。它需要“Boost”和“TBB”c++库。文件中的“Makevars”文件中正确设置了这些库的路径。/src”文件夹,或者它们可以在标准系统路径中找到。从终端安装到INSTALL_PATH文件夹,使用命令(仅限linux用户):
cd PACKAGE_SOURCE_FOLDER
R CMD INSTALL -l /INSTALL_PATH ./ --preclean
一旦你(成功)安装了 R 包,让我们从用例开始。我选择保持描述相对较短,以避免与 github 非常冗余。如果您有兴趣,请注意代码仍在开发中,正在等待外部贡献者使其成为大型树集成模型的 CF 可解释性的一个很好的包,这些模型有一天可能会在 XGBoost 的代码中占有一席之地(是的,作者是个梦想家……)。
作为第一个示例,让我们考虑一个用于消费者信贷批准/拒绝的数据集。与我在文章开头宣传的工业故障检测场景截然不同,但 CF 可解释性方法可以扩展到任何由正常类别(信用批准)和“异常”类别(信用拒绝)组成的分类场景)。此外,小数据集很好地展示了一些东西,学术界几十年来一直在使用它们(这是一个可靠的论点吗?)。该数据集允许学习 20 个输入特征之间的映射,例如持续信用的数量、收入、年龄、信用的目的……以及授予与否的决定。
我为您提供了 XGBoost 模型的所有特征格式和训练细节,您可以轻松地从演示脚本中对它们进行逆向工程。让我们直接跳到 CF 示例计算。我们首先需要选择与信用拒绝相对应的测试数据点。我们检查它是否被分类并标记为“信用拒绝”。为了确保后者,我们只看基本事实。训练后的模型在两类准确率方面确实不会高于 75%,因此存在许多误报(意味着被归类为“信用拒绝”的点,而实际上并非如此)。给定一个我们称之为“查询点”的选定点,我们计算其关联的最接近的 CF 示例。下面,我将解释用于确定 CF 示例的函数中每个参数的含义。我觉得有必要在这里做,因为它在代码中缺少解释。
CF_search <- function(query, # query point
predicted_class, # predicted class of the query
target_class = -1, # targeted class for the CF example
tree_list, # dumped XGBoost model under a "(Boxes, Scores)" format
max_depth, # maximal depth of tree set to learn the XGBoost model
nb_class=2, # number of classes in the classification problem at hand
nb_trees_per_class, # refers to the "nrounds" parameter of XGBoost. The total number of trees in the model will be "nb_trees_per_class*nb_class"
thresh_dec=0.5, # decision threshold (for binary classification problems)
sup_d2query_dataset, # upper bound on the distance of the query to the closest CF example (square distance)
budget=2e7, # maximal number of elementary 1D intersection problems that will be solved (corresponds to the maximal number of nodes that are constructed in the tree-like decomposition structure)
max_dim_width_first=12, # index of dimension in which the decomposition algorithm stops the width-first exploration and starts with depth-first one
check_has_target=TRUE, # checking in each node of the decomposition tree if there a possibility that it produces a target region in the end. If not, stopping the construction in this node.
update_sup_bound=TRUE, # updating the sup bound in all threads each time a depth-first exploration in a thread finds an upper bound that is tighter than the current one
model_type = "binary:logistic", # XGBoost model type
nb_rec_iter=2, # number of search rounds (setting more than 1 here often allows to find the exact CF problem solution in difficult cases)
tol=1e-7, # stopping criterion referring to the possibility of doing "nb_rec_iter" iterations
cheap_try=-1 # useful to start with an upper bound that is overly tight. If no CF example is found within this bound, it is enlarged, and serach iteration are performed as in the normal case.
)
下表显示了三个人的一些结果。每次我们提到查询点(客户端状态),以及相关的 CF 示例(推荐 + 受限推荐)。当查询点和 CF 示例之间没有变化时,单元格留空。对于每个人,我们计算两个 CF 示例。第一个(“推荐”行)对应于“完全可操作性”场景,即个人可以控制/改变与自己有关的所有特征。第二个对应于“部分可操作性”场景,即个人只能控制/改变几个变量。例如,尽管对年轻化乳液的研究取得了很大进展,但考虑到个人无法控制自己的年龄更为现实。
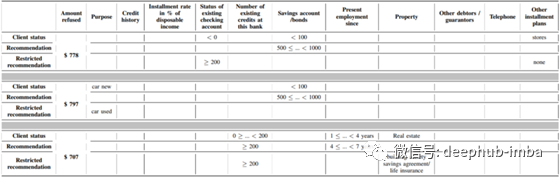
对于三个不同的人,我们诊断了银行拒绝他们要求的信贷的决定,并展示了 CF 方法提供的建议,即他们需要更改最小值以便向他们授予信贷。对于每个人,我们提出两个建议:第一个建议认为个人有可能控制/改变所有特征(“推荐”行)。第二个认为个人只能控制有限数量的特征(“限制推荐”行),这通常更现实(例如,个人不能对他的年龄或婚姻状况做出任何改变)。
第二个用例涉及 MNIST 数据集的错误分类数字。我们从这十个类中提取两个类,它们本质上是模糊的(例如 1 和 7,或 5 和 6)。然后,我们训练一个二类分类 XGBoost 模型,该模型学习区分这两个类。作为查询点,我们选择属于一个类的一个点,该点在另一类中被模型错误分类。我们还确保输入数字在视觉上是模糊的(这意味着人眼无法真正分辨它属于哪个类)。最后一点特别重要,因为我们的目标不是检测分类模型的潜在弱点,而是检测输入数据中异常值的存在。所以,我们需要能够认为输入数据在某种程度上是错误的,而分类器只是在做它的工作。只有在这些假设下,我们才能在未分类数据和错误数据之间进行比较,并将我们的 CF 方法应用于未分类示例,就像我们对错误数据所做的那样。
在这个用例中,我们引入了另一个方面:合理性的概念。为了使 CF 示例更合理(即在视觉上更具说服力),我们可以在与模型对 CF 示例的预测相对应的决策分数上添加约束。通过强制模型更有信心地预测正确的类,我们获得了 CF 示例,它看起来越来越接近正确类的元素(“正确的类”,我指的是与地面中的查询点相关联的类真相)。加强合理性会损害失真,这意味着较高的合理性会导致 CF 示例在欧几里德距离方面离查询点更远。下图说明了这个想法。

考虑两个二元分类问题(5 对 6 和 4 对 9)。第一行:模型将“5”错误分类为“6”的示例。初始查询图像显示在左侧。我们使决策阈值在 0.5 和 0.2 之间变化。获得被模型以更高置信度归入正确类别的 CF 示例是以引入初始查询数据的失真为代价的,即决策阈值“eps”越低,与初始查询的距离越大 查询“dCF”。从视觉上看,我们看到 CF 方法对初始查询数据进行了合理的更改,使其看起来更像“5”。第二行:模型将“4”错误分类为“9”的示例。
也可以强制执行其他合理性标准:例如,我们可以检查找到的 CF 示例是否位于包含训练数据集中至少一个元素的最大交叉区域中。这将避免选择在现实生活中不切实际/无法达到的分布外 CF 示例。
最后,考虑查询点与其对应的 CF 示例之间的欧几里德距离不是强制性的。也可以考虑其他距离,而无需更改分解算法,前提是这些距离可以表示为坐标加法,即计算为:“d(X, Y) = g( ∑ di(X[i ], Y[i]) )”,其中“di”是应用于第 i 个坐标的特定操作,“g”是递增的单调函数。例如:di(X[i], Y[i]) = (Y[i]- X[i])² 表示平方欧几里得距离。
好吧,从这篇很长的博客文章中要记住什么(抱歉,我在第一次尝试与世界交流时可能过于冗长)。首先,该树集成模型允许计算精确的 CF 示例,同时是故障检测的绝佳模型(尤其是梯度提升树)。其次,CF 示例除了定位故障/异常外,还给出了纠正它所需采取的最小行动的精确概念。此外,这里提供的 CF 方法具有产生稀疏解释的巨大优势,即对减少的输入特征数量提出更改建议,这使得解释对于人类用户来说更容易理解。
在下一篇文章中,我将向您展示 CF 对回归问题的解释的扩展,并教您(如果您愿意的话)如何部署 CF 推理以实现利润最大化,或者,至少,如何制定销售价格只需改变厨房地毯地板的颜色,您的房子就会上涨 10 000 美元。好吧,我说得太多(或说得不够),但如果第一篇文章成功,我会为您提供更详细的解释:)。
最后本文代码在这里:https://github.com/PierreBlanchart/CMBDTC
作者:Pierre Blanchart