1 赛题
B题 城市轨道交通列车时刻表优化问题
列车时刻表优化问题是轨道交通领域行车组织方式的经典问题之一。列车时刻表规定了列车在每个车站的到达和出发(或通过)时刻,其在实际运用过程中,通常用列车运行图来表示。图 1 为某一运行图的示例,图中每一条线表示一趟列车,横轴表示车站,纵轴表示时间,每一条线反映了一趟列车在不同时刻所处的相对位置,也称为运行线。比如,图中红色运行线表示,列车于 9:02 分从 D 站出发,于 9:05 分到达 C 站,停留 1分钟后出发,于 9:09 分到达 B 站,停留 1 分钟后出发,于 10:03 分到达A 站。
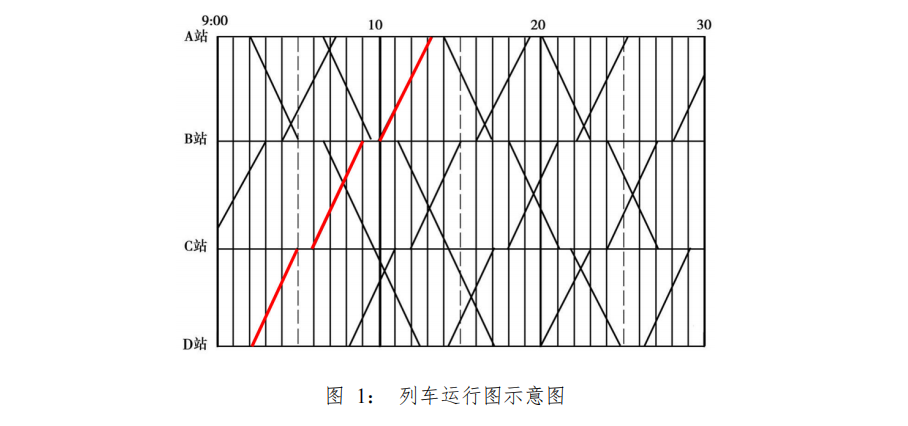
实际运营中,在铺画列车运行图之前,首先得先确定列车开行方案,列车开行方案包括列车编组方案、列车停站方案和列车交路计划三部分。
列车编组方案规定了列车的车型和编组数量(即列车的节数),在本问题中采用统一的车型和编组数量。
列车停站方案是规定列车在哪些站点停站的方案,在本问题中均采用站站停的停站方案(即列车在每个经过的车站都会停车)。
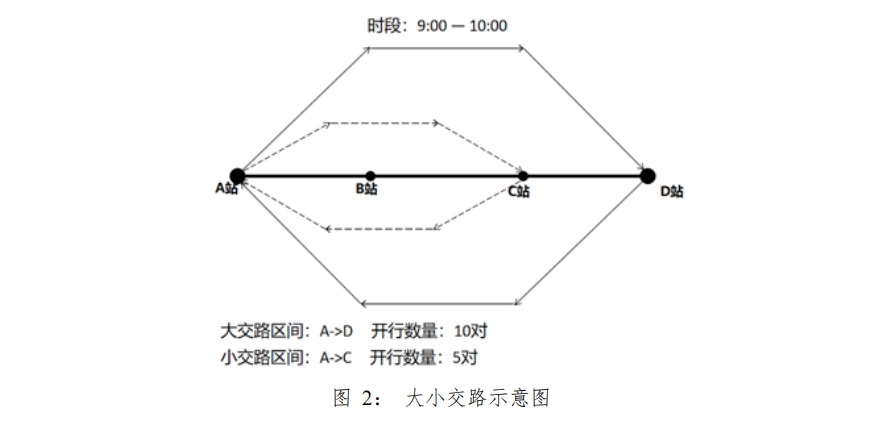
列车交路计划是指列车在规定的运行线路上往返运行的方式,即规定了列车在哪些站点之间运行以及开行的数量。大小交路模式是城轨运营中常用的交路模式,是指城市轨道交通运行线路的长短区间。通俗讲,大交路是指列车跑完全程,小交路是指将全程中的某两个站作为临时起点或终点来跑,需要注意的是,只有具有折返能力的车站(能让列车调头的车站)才能作为交路的起点或终点。图 2 为某大小交路方案示意图,表示以 A 站为起点的,D 站为终点大交路区间开行 10 对列车,以 A 站为起点,C 站为终点小交路区间开行 5 对列车。
在大小交路方案中,大小交路列车开行列数通常为 1:n 或 n:1 两种模式,即每开行 n 列大(小)交路列车后,开行一列小(大)交路列车,并且小交路所经过的车站数量需有一定限制:小交路区间过短会导致列车的折返频繁,使运营成本增加;小交路区间过长则无法体现大小交路运营模式的作用。

在列车开行方案的制定中,需要以最小的企业运营成本和最大的服务水平(乘客在车时间和乘客等待时间)来满足客流的需求,企业的运营成本包括固定成本(所需车辆的数量)和变动成本(列车总走行公里)两部分组成。受到车站通过能力的制约和服务水平的要求,在一定时间内,列车的发车数量也有一定的限制。
在制定好列车开行方案后,可根据该方案同样以企业运营成本最小化和服务水平最大化为目标铺画列车运行图,即确定每趟列车的出发和到达的具体时刻。现有的列车时刻表通常为等间隔的平行运行图,即发车间隔(如每 5 分钟开行一趟列车)和在同一站点的停站时间相等。发车间隔的长短会有一定的限制:发车间隔过短,则会影响列车运行的安全;发车间隔过长,则会增长乘客的平均等待时间,从而影响服务水平。同样地,停站时间也需受到一定限制,一般来说列车在车站的停站时间正比于在该站上、下车的乘客数量。另外,需要注意的是,两列车在同一区间追踪运行时,需保留一定的安全间隔(追踪间隔时间)。
采用大小交路运营模式的列车运行图,大交路列车和小交路列车一般会交替开行,比如当大交路列车与小交路列车的比例为 2:1 时,则会以每3 列车为一个组合(前 2 列车为大交路列车,第三列车为小交路列车)滚动发车。
在下列问题中,只需制定单向的列车时刻表即可。
问题一:在满足客流需求的条件下,以企业运营成本最小化和服务水平最大化为目标,制定列车开行方案。即确定大交路区间列车的开行数量,小交路的运行区间以及开行数量。(输出格式详见附件 6)
问题二:在问题一制定的列车开行方案下,同样以企业运营成本最小化和服务水平最大化且尽量满足客流需求为目标,制定等间隔的平行运行图。(输出格式详见附件 7,并将附件 7 单独上传到竞赛系统中)
问题三:对于降低企业运营成本和提高服务水平,你们团队有哪些好的方法或建议?基于客流和车站数据,提供相应的量化分析支持。
2 解题思路
1) 公交车的平均速度为20公里/小时;按某种程度不考虑停车时间,从而也不考虑乘客上下车所用时间,或虽然有不同的停车时间都认为计入平均速度之内;
(2) 只讨论了18个单位时间段上、下车情况:记上行方向各站点上车总人数为a,a,a……,a,上行方向各站点下车总人数分别为b,b,b……,b;下行方向在求解也做同样的设定.
(3) 定义上下差数c如下:
……
一般地,
(4)由于公共汽车站在单位时间内来站乘车地人数使一个服从于Poisson分布的随机变量,设上、下车总人数(或)是此随机变量的平均值;(…13)
(5)在每个单位时间段中,上、下车总人数(或)是均匀分布在时间区间内,即时间区间等分:,个人依次在每个小区间中点到达.
(6)在公交车运行中,每一时间段的每一个站点都以最大可能地让乘客上车,而不顾及后面乘客地利益(即不考虑后面乘客能否上车).
(7)假设在行车过程中,不会出现车坏、道路严重阻塞等意外事故.
(8)本题所提供的是一个典型工作日的统计表,故具有普通意义.
注意:符号约定中没有定义而在文中出现的,在第一次出现处均有说明.
本问题是一个给出上、下行两方向每一个时间段,每一个站点上、下车总人数的统计数,由这些数据,按照多种要求和条件来设计一个便于操作的全天(工作日)的公交车调度方案,并抽象出一个明确的、完整的数学模型.
对于上行方向:
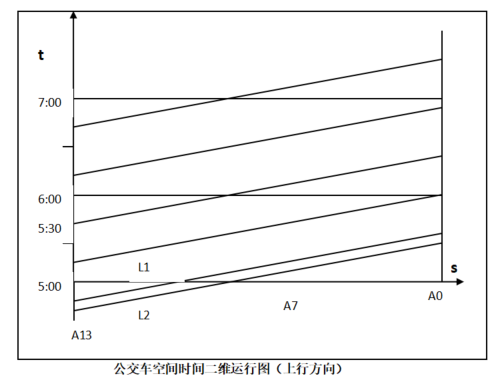
记上车的总人数矩阵为,下车的总人数矩阵为,在这里的(或)是随空间(公交车路线)和时间变化的量,因此,根据问题所提出的公交车行进情况,我们把公交车行进过程中的空间(地点)与时间的情况反映在坐标轴上,即以直角坐标系的横轴表示各站点距离,纵轴表示各时刻.由此,我们可以做出一个公交车空间与时间的二维运行图,公交车运行的轨迹在图上的反映是一簇平行的直线簇,它们的斜率为,即速度的倒数;(见附图),平行直线簇可以直观地反映出公交车行车时各站与时间关系,以及公交车跨时段的行车情况.(下行方向运行图类似)
篇幅有限,详细思路更新到文档中


🥇 最新思路更新(看最新发布的文章即可):
https://blog.csdn.net/dc_sinor?type=blog
3 最新思路更新
🥇 最新思路更新(看最新发布的文章即可):
https://blog.csdn.net/dc_sinor?type=blog
版权归原作者 建模君Assistance 所有, 如有侵权,请联系我们删除。