10、Java 方法的递归调用详解（递归调用的分析和案例：阶乘、斐波那契、猴子吃桃）

文章目录

一、递归缩写

🌱 YAML：是 SpringBoot 框架推荐的一种配置文件，它的全称是【YAML Ain’t a Markup Language（YAML 不是一种标记语言）】，可以看到 YAML 是一个句子的递归缩写。

🌱 GNU：是一个自由的操作系统，其内容软件完全以 GPL 方法发布，但它不包含具著作权的 Unix 代码。它的全称是【GNU’s Not Unix（GNU 并非 Unix）】，GNU 也是一个句子的递归缩写。

二、递归调用

思考：如何计算 [1, n] 范围内的整数的累加和 ?

下面的代码通过【循环】的方式计算 [1, n] 范围内的累加和，本篇文章学习另一种求累加和的方式：递归求和

publicclassRecursionTest{publicstaticvoidmain(String[] args){// sumByCircular = 15
        System.out.println("sumByCircular = "+sumByCircular(5));}/**
     * 通过【循环】计算 [1, n] 范围内的整数的累加和
     */privatestaticintsumByCircular(int n){int sum =0;for(int i =1; i <= n; i++){
            sum += i;}return sum;}}

🍉【分析】求 [1, n] 范围的累加和，可以理解为求 [1, n-1] 范围的累加和, 然后再加 n **
🍉 如：求 [1, 5] 范围的累加和可如下思考：
🍉 ① 求 [1, 5] 范围的累加和，可以理解为求 [1, 4] 范围的累加和, 然后再加 5 **
🍉 ② 求 [1, 4] 范围的累加和，可以理解为求 [1, 3] 范围的累加和, 然后再加 4 **
🍉 ③ 求 [1, 3] 范围的累加和，可以理解为求 [1, 2] 范围的累加和, 然后再加 3 **
🍉 ④ 求 [1, 2] 范围的累加和，可以理解为**求 [1, 1] 范围的累加和, 然后再加 2 **

(1) 递归方式求累加和

使用【递归】计算 [1, n] 范围内的整数的累加和的代码：

publicclassRecursionTest{publicstaticvoidmain(String[] args){// sumByRecursion = 21
        System.out.println("sumByRecursion = "+sumByRecursion(6));}/**
     * 使用【递归】计算 [1, n] 范围的累加和
     */privatestaticintsumByRecursion(int n){if(n <=1)return1;// 递归终止条件return n +sumByRecursion(n -1);}}

如果递归没有终止条件 ❓
StackOverflowError（栈溢出）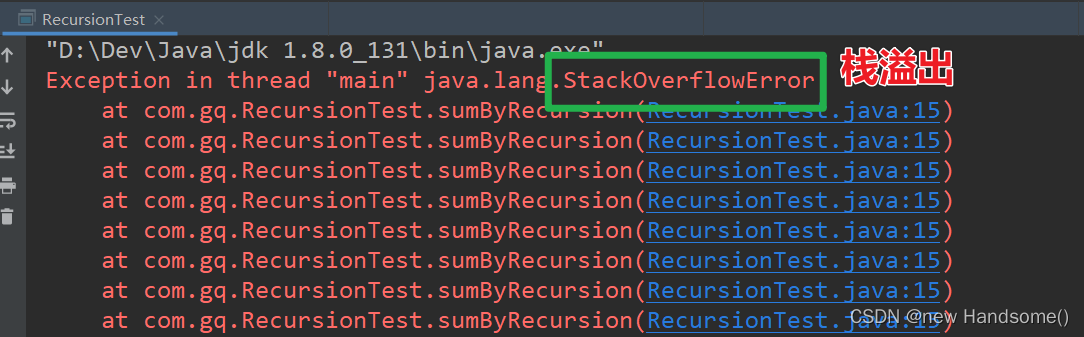

(2) 递归内存分析

int sum = sumByRecursion(3);

执行上面代码，JVM 栈空间情况如下图：

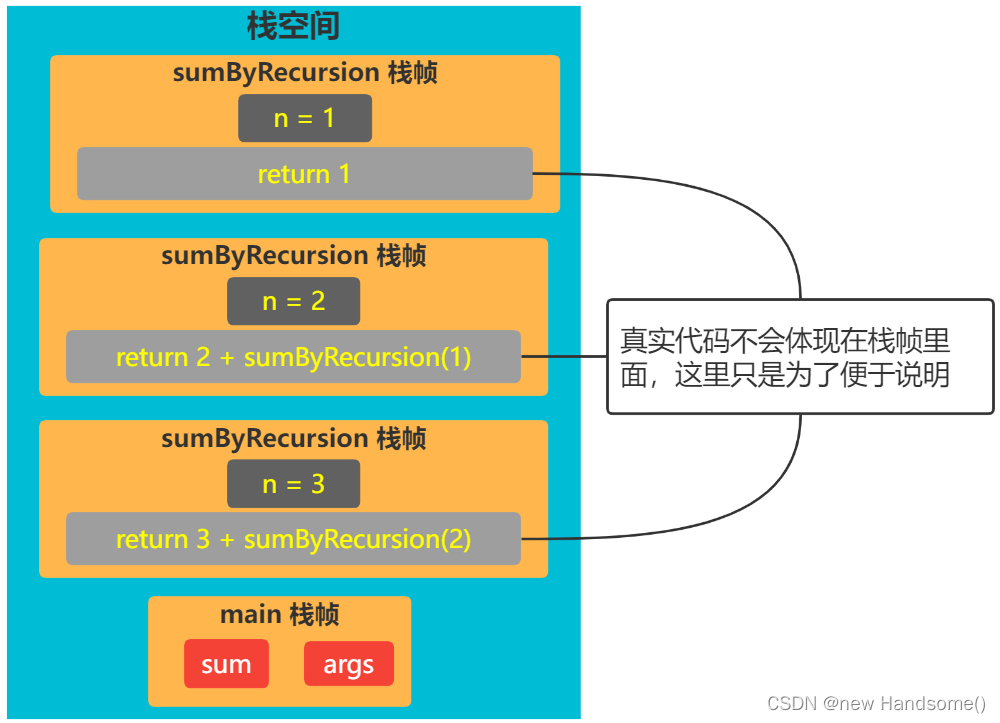
🥤 递归调用若没有终止条件，将会一直消耗栈空间
🥤 最终会导致栈内存溢出（Stack OVerflow）
🥤 递归必须要有一个明确的终止条件（边界条件、递归基）

三、递归调用（概念）

🍬方法中调用方法本身，每次调用时传入不同的参数。
🍬 递归提供编程者一个解决复杂问题的思路。

四、递归调用举例

看下面的代码, 思考输出结果：

publicclassRecursionDemo{publicstaticvoidmain(String[] args){test(5);/*
           output: 
                   n = 2
                   n = 3
                   n = 4
                   n = 5
        */}privatestaticvoidtest(int n){if(n >2){test(n -1);}
       System.out.println("n = "+ n);}}

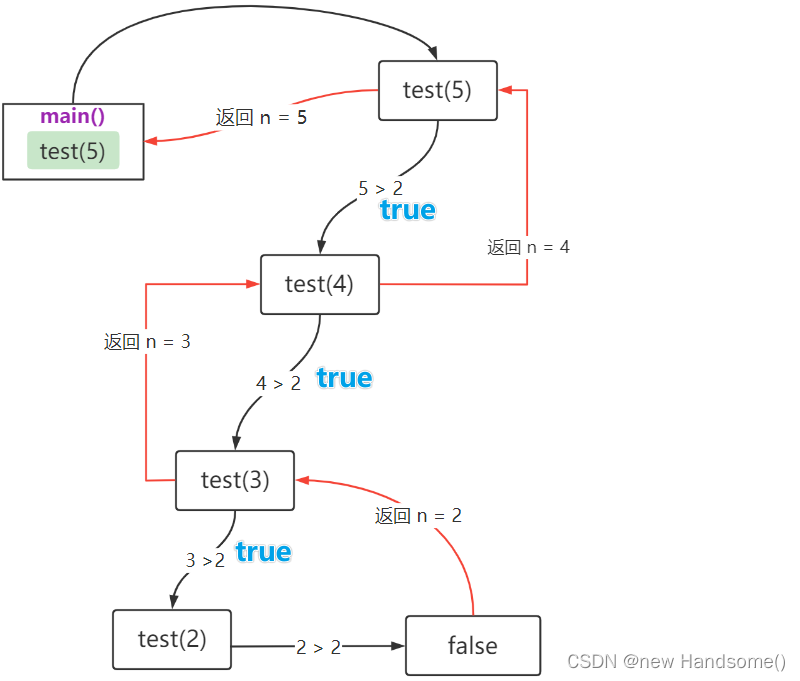
publicclassRecursionDemo{publicstaticvoidmain(String[] args){test(5);// 只输出：n = 2}privatestaticvoidtest(int n){if(n >2){test(n -1);}else{
            System.out.println("n = "+ n);}}}

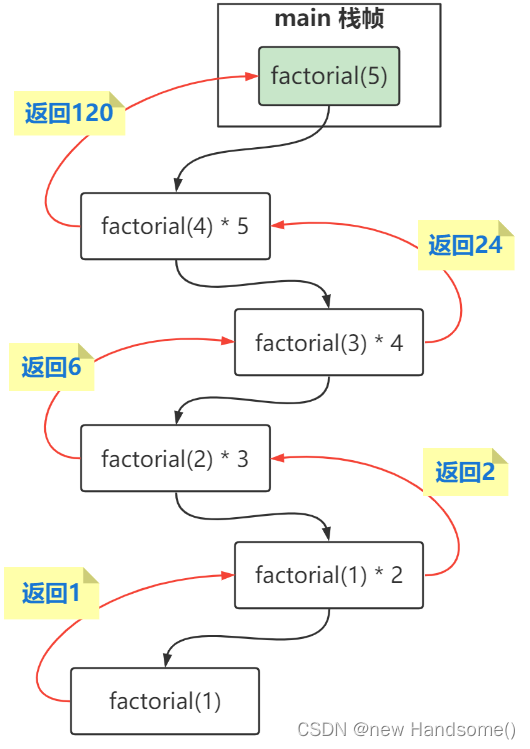
通过递归计算阶乘：

publicclassRecursionDemo{publicstaticvoidmain(String[] args){int result =factorial(5);// result = 120
        System.out.println("result = "+ result);}privatestaticintfactorial(int n){// 如果 n 小于等于 1, 默认认为阶乘结果是 1 if(n <=1)return1;returnfactorial(n -1)* n;}}

五、递归注意事项

📖 调用方法会在栈空间分配一块新的、独立的、受保护的栈空间（栈帧）
📖 方法的局部变量是独立的，不会相互受影响
📖 调用递归方法的参数必须向退出递归的条件逼近，否则会导致无限递归，进而导致 StackOverflowError（栈溢出）

六、斐波那契数列

斐波那契数列数的几何模型在大自然、化学、生活中经常存在。

📒 斐波那契数列：Fibonacci sequence
📒 斐波那契数列：黄金分割数列
📒 斐波那契数列： 兔子数列
📒 斐波那契数列：由数学家莱昂纳多 斐波那契提出的

斐波那契数列描述：有一列数，前两个数是1，从第3个数开始，后面的数都是它的前面的两个数之和，如此规则构成的一系列数就是斐波那契数列。
斐波那契数列举例： 1、1、2、3、5、8、13、21、34、55、89

用代码实现：输入一个数字（代表斐波那契数列的第几项），打印斐波那契数列第几项的值

publicclassRecursionDemo{publicstaticvoidmain(String[] args){// 89
        System.out.println(fibonacci(11));}/**
     * 递归求斐波那契数列的第 n 项的值
     */privatestaticintfibonacci(int n){if(n <=2)return1;returnfibonacci(n -1)+fibonacci(n -2);}}

递归方式实现斐波那契数列非常地不合适，但也是一种方法（以后讨论它的另外一种方法）

七、猴子吃桃

Monkey 有一篮子的桃子 🍑，不知具体多少个。
Monkey 第一天吃了桃子 🍑 总数的一半，并多吃一个。
以后猴子 🐒 每天都吃其中的一半，并多吃一个。
第十天的时候就只有1个桃子了。
问：篮子里面一开始有多少个桃子🍑 ？

分析:

🔑 已知条件：
① 第十天只有1个桃子
② 每天吃当前桃子总数的一半，并多吃一个
🔑 推导
令 day(n) 是第 n 天的桃子数
① day(10) = 1
② day(9) = 4 【day(9) / 2 - 1 = day(10)】第9天的桃子数的一半，再减1要等于第10天的桃子数
③ day(8) = 10 【day(8) / 2 - 1 = day(9)】第8天的桃子数的一半，再减1要等于第9天的桃子数
④ day(7) = 22 【day(7) / 2 - 1 = day(8)】第7天的桃子数的一半，再减1要等于第8天的桃子数
⑤ day(6) = 46 【day(6) / 2 - 1 = day(7)】第6天的桃子数的一半，再减1要等于第7天的桃子数
…
🔑 通项公式
day(n) = day(n-1) / 2 - 1【当天的桃子数等于前一天的桃子数减一半，再减1】
化简得：day(n-1) = (day(n) + 1) * 2 【前一天的桃子数等于当天的桃子数加1之后乘以2】
最终：day(n) = (day(n +1) + 1) * 2【当天的桃子数等于后一天的桃子数加1后乘以2】

代码实现：

publicclassMonkeyPeachDemo{publicstaticvoidmain(String[] args){// 第1天的桃子数：1534
        System.out.println("第1天的桃子数："+dayPeach(1));}privatestaticintdayPeach(int d){if(d ==10)return1;return(dayPeach(d +1)+1)*2;}}

若发现错误，请不吝赐教。Have a nice day!