基于人工噪声的无线通信物理层安全研究

引言

    无线通信的普及性源于它的广播特性，能够让用户不受地理位置随时随地获取信息。但是这种广播特性同时也让窃听者窃取信息变得容易又隐蔽，无线通信的安全性因此很难保证。同时，无线信道的不确定性和时变性也给无线通信带来了新的挑战，但是，如果能合理利用无线信道的物理属性，反而有可能给安全通信带来新的生机。

    香农奠定了安全通信的基础，证明了只有密钥长度大于等于信息长度时才能实现完美保密，其中潜在条件是[引用 :Shannon Communicaion theory of secrecy systems ]

• 窃听者有无线的计算能力和时间

• 接收者和窃听者收到的信号相同

    传统密码系统往往忽略了物理层的作用，只对信息层进行加密和解密保证安全，只有发送者和接收者才知道密钥，窃听者必须从接收信号推断密钥，由此获取私密信息，然而，根据上述香农的研究成果，密码不能小于明文的长度。因此，如果使用一个较短的信息密钥，那么加密算法的安全性关键前提是窃听者的计算资源和计算时间有限。
  
    在很多实际系统中，窃听者信道往往比接收者要差，例如搭线窃听模型，会面临来自用户信道和窃听者自身信道的噪声，如果信道是一个相对于用户信道的退化信道，那么接收者能以一个非零的信息速率实现完美保密，这时系统用保密容量刻画，他表示完美保密条件下的最大可达信息速率。与密码学不同，这里的安全性是“可证明的”，其安全性的结论是通过信息论的工具得到的，这种形式的安全称为信息论安全，这种情形下，安全性的保证和物理层模型息息相关。
  
    在广播媒质中，一般情况下窃听者和接收者会有各自不同的信道，这时搭线窃听不再适用，当窃听信道比用户的接收信道差时，完美安全能够以一个非零的速率实现，然而在无线环境中无法保证窃听信道一定会比接受信道差(窃听者更近或采用增益天线)，如果接收信道比窃听信道差，那么保密容量为零，可证明的安全此时无法保证，那么如何设计一种通信系统以对抗窃听者的信道优势呢，本文提出一种利用多个天线提供的自由度来增强保密通信的速率，本质上是引入了人为不确定性或人工噪声。
  

保密容量

    首先给出信息论安全模型中的共同假设条件，与密码学不同，这里假定发送者和接收者不再需要共享密钥，此外，需要必要的身份认证，即发送者和接收者可以互相验证对方的身份，假定窃听者是被动的，只听不发。

    假定通信双方和窃听者可以精确估计自己的信道；假定发送者通过反馈知道接收者的信道，但不知道窃听者的信道，也不知道窃听者的位置，或窃听者是否存在。因此，本文研究的是在发送者不知道窃听者信道增益的假设条件下的保密通信。

搭线窃听模型

    搭线窃听模型假设窃听者用搭线窃听的方式对接收者的信道进行窃听，因此接收到的信号是接收者信号的退化版本，此情形下，实现无共享密钥保密通信的关键要素是窃听者的信道比接收者的信道差，而且搭线窃听模型仅适用于有线系统。

    发送者将一个包含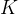![K](https://latex.csdn.net/eq?K)个符号的保密信息编码成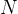![N](https://latex.csdn.net/eq?N)个编码符号，也就是说保密消息![m^K](https://latex.csdn.net/eq?m%5EK)被编码成符号![x^N](https://latex.csdn.net/eq?x%5EN)，这是接收者的信道输入。接收者的信道输出是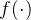![z^N](https://latex.csdn.net/eq?z%5EN)=![f(x^N)](https://latex.csdn.net/eq?f%28x%5EN%29)，其中![f(\cdot )](https://latex.csdn.net/eq?f%28%5Ccdot%20%29)是一种随机映射。接收者基于![z^N](https://latex.csdn.net/eq?z%5EN)估计保密信息。![z^N](https://latex.csdn.net/eq?z%5EN)又是搭线窃听信道的输入，![y^N](https://latex.csdn.net/eq?y%5EN)=![g(z^N)](https://latex.csdn.net/eq?g%28z%5EN%29)是窃听者观察到的输出，其中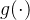![g(\cdot )](https://latex.csdn.net/eq?g%28%5Ccdot%20%29)是另一种随机映射。窃听者试图基于![y^N](https://latex.csdn.net/eq?y%5EN)对保密信息进行译码。

    保密信息的速率由![R=H(m^K)/N](https://latex.csdn.net/eq?R%3DH%28m%5EK%29/N)给出，这是每个保密信息符号的熵。窃听者在观察到![y^N](https://latex.csdn.net/eq?y%5EN)后，关于保密信息的不确定性是通过每信源符号的疑义度度量的。为了简化符号，用每信源符号的信源熵来归一化疑义度，得到分数疑义度为![\bigtriangleup =H(m^K|y^N)/H(m^K)](https://latex.csdn.net/eq?%5Cbigtriangleup%20%3DH%28m%5EK%7Cy%5EN%29/H%28m%5EK%29)。在![\bigtriangleup](https://latex.csdn.net/eq?%5Cbigtriangleup)=1时具有特殊的意义，因为![\bigtriangleup](https://latex.csdn.net/eq?%5Cbigtriangleup)=1确保了窃听者在观察![y^N](https://latex.csdn.net/eq?y%5EN)后与观察![y^N](https://latex.csdn.net/eq?y%5EN)前相比没有差别，即窃听信道的输出不增加窃听者对保密消息的任何知识。因此![\bigtriangleup](https://latex.csdn.net/eq?%5Cbigtriangleup)=1时完美保密是可实现的。从本质上讲，完美安全是指接收者能够译码保密信息且误码概率小到可以忽略，而窃听者无法译码保密信息。进而，保密容量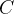![C](https://latex.csdn.net/eq?C)定义为完美安全条件下的最大可达速率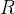![R](https://latex.csdn.net/eq?R)。

    参考文献[6]给出了高斯搭线窃听信道的保密容量的显性表达式。假定接收者和窃听者的信道均为加性高斯白噪声（AWGN）信道，其信道输出为

    其中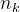，![n_k](https://latex.csdn.net/eq?n_k)和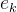![e_k](https://latex.csdn.net/eq?e_k)均为独立同分布AWGN，且彼此独立，方差分别是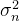![\sigma _n^2](https://latex.csdn.net/eq?%5Csigma%20_n%5E2)和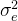![\sigma _e^2](https://latex.csdn.net/eq?%5Csigma%20_e%5E2)，因此，发送者和窃听者之间的信道可等效为噪声方差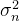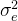![\sigma _n^2](https://latex.csdn.net/eq?%5Csigma%20_n%5E2)+![\sigma _e^2](https://latex.csdn.net/eq?%5Csigma%20_e%5E2)的AWGN值。平均输出功率约束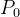![P_0](https://latex.csdn.net/eq?P_0)（在长度为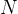![N](https://latex.csdn.net/eq?N)的码字上）为

    ![\tfrac{1}{N}\sum_{i=1}^{N}E[X_i^2]\leqslant P_0](https://latex.csdn.net/eq?%5Ctfrac%7B1%7D%7BN%7D%5Csum_%7Bi%3D1%7D%5E%7BN%7DE%5BX_i%5E2%5D%5Cleqslant%20P_0)

    这种高斯搭线窃听信道模型的保密容量为

    这种情形下，保密容量为接收信道和窃听信道容量的差，此外，请注意到只要![\sigma _e](https://latex.csdn.net/eq?%5Csigma%20_e)>0，即窃听信道是退化的，保密容量对任何功率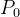![P_0](https://latex.csdn.net/eq?P_0)就都为正。问题的重点在于非零保密容量是否只在搭线窃听模型中才存在

广播模型

    参考文献[4]提出了一个更一般的广播信道模型，这里的窃听信道不必是接收者信道的退化版本，其中，接收者和窃听者有各自的信道，![x^N](https://latex.csdn.net/eq?x%5EN)是两个信道的输入，接收者和窃听者信道输出分别是![z^N](https://latex.csdn.net/eq?z%5EN)和![y^N](https://latex.csdn.net/eq?y%5EN)。该模型更适合无线广播通信信道的场合。同样，用疑义度定义完美保密，保密容量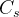![C_s](https://latex.csdn.net/eq?C_s)定义为完美保密时的保密信息发送到接收者的最大可达速率

其中，最大值在随机变量U，X的联合分布中取到，U，X满足马克可夫链U->X->YZ。上式中需要最大化的项是发送-接收与发送-窃听之间的互信息之差。本章的重点是研究无线通信道的保密通信，所以将沿用上式结论。然而，窃听者可以利用无线介质的物理属性，极力使它的信道不逊于接收者的信道，从而迫使保密容量为0，例如，窃听者会比接收者更接近发送者。

仿真验证

    考虑一个简单的例子，其中包括发送者，接收者，窃听者在内的所有节点都只有单个天线。假设发送-接收和发送-窃听信道均为平坦衰落信道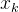，![x_k](https://latex.csdn.net/eq?x_k)是时刻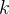![k](https://latex.csdn.net/eq?k)的发送符号，而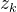![z_k](https://latex.csdn.net/eq?z_k)和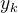![y_k](https://latex.csdn.net/eq?y_k)分别是接收者和窃听者在时间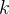![k](https://latex.csdn.net/eq?k)的信道输出，其关系如下

其中，和分别是接收者和窃听者的时变信道增益。和是方差分别为和独立同分布加性复高斯白噪声。假设一个块衰落模型，即和在多符号块的传输期间保持不变，不同块之间的和是相互独立的。假设和在一个多符号块中是常数，则可在每个块中套用信息论的结果式。变量和在块与块之间的变化可以用来刻画无线信道的时变性（假设是慢变的）。块间的和为复数，是独立同分布的高斯分布（瑞利衰落），且相互独立，接收者的平均信噪比由给出。同样，窃听者的平均信噪比由给出

    保密容量为

其中，。需要注意的是容量是随机变量，因为他们依赖于随机变量和。

    这里用中断概率来评估系统安全性能。当保密容量小于某个固定值（定义为中断容量）时候，则称发生了中断，其概率为中断概率。保密需求就可用对应于期望中断容量的某个中断概率来度量，例如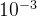![10^{-3}](https://latex.csdn.net/eq?10%5E%7B-3%7D)。若用容量表示，则对应于某个中断容量![C_{outage}](https://latex.csdn.net/eq?C_%7Boutage%7D)的中断概率定义为![Pr(C<C_{outage})](https://latex.csdn.net/eq?Pr%28C%3CC_%7Boutage%7D%29)。

    为研究保密容量的规律，这里考虑一个特定的场景。c=20dB，一旦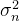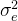![|h_k|\leqslant |g_k|](https://latex.csdn.net/eq?%7Ch_k%7C%5Cleqslant%20%7Cg_k%7C)，假设（![\sigma _n^2](https://latex.csdn.net/eq?%5Csigma%20_n%5E2)=![\sigma _e^2](https://latex.csdn.net/eq?%5Csigma%20_e%5E2)）,保密容量将是0。由问题的对称性，很容易得出此事件的概率是1/2，显然![SNR_e](https://latex.csdn.net/eq?SNR_e)较大时性能会更差。

    容量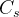![C_s](https://latex.csdn.net/eq?C_s)的中断概率随着![SNR_e](https://latex.csdn.net/eq?SNR_e)的变化如下图所示。容量通过奈特/符号来衡量，而不是比特/符号，这意味着使用![\log_e(\cdot )](https://latex.csdn.net/eq?%5Clog_e%28%5Ccdot%20%29)来计算熵。![SNR_r](https://latex.csdn.net/eq?SNR_r)固定在20dB，而![SNR_e](https://latex.csdn.net/eq?SNR_e)从10dB变化到30dB。较高的![SNR_e](https://latex.csdn.net/eq?SNR_e)意味着窃听者更接近发送者，这会导致更高的中断概率。对于保密容量，即使窃听信道比合法信道差10dB时，对应于中断容量0.01，中断概率才勉强达到![10^{-1}](https://latex.csdn.net/eq?10%5E%7B-1%7D)。对于合法信道比接收信道差的情况，由图中![SNR_e](https://latex.csdn.net/eq?SNR_e)=30dB的曲线图可以证实，当![SNR_e](https://latex.csdn.net/eq?SNR_e)较大时性能极差，且随着![SNR_e](https://latex.csdn.net/eq?SNR_e)的增加性能下降非常迅速。

    我们期望系统能在一个不算低的容量情况下，维持一个低水平的中断概率，以满足系统的保密通信需求，由下图可知，在传统方案下这非常困难，我们提出一种新方案，通过多个天线提供的自由度将人工噪声添加到保密信息中，降低窃听者的接收信噪比，同时，人工噪声又不影响接收信道，因此不会对合法接收者产生影响。

中断容量和中断概率（加噪声前）

人工噪声系统

    本节正式提出系统模型及其表示方法。首先描述场景，然后讨论模型假设，本章用加粗字体标记向量和矩阵，用![\dagger](https://latex.csdn.net/eq?%5Cdagger)表示Hermitian运算符。

场景

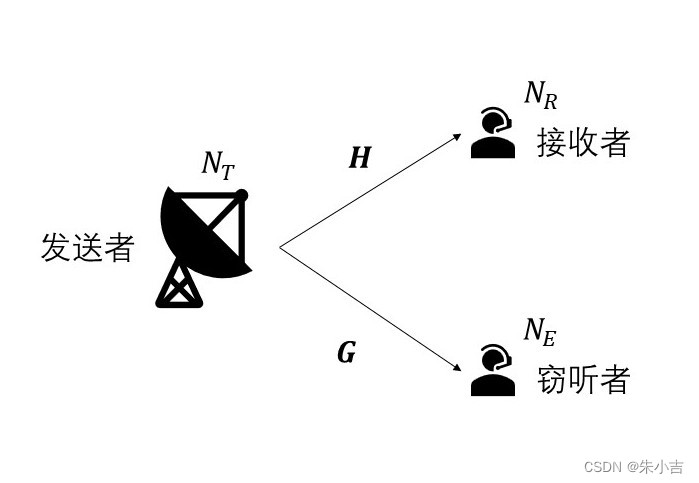
模型示意图

     考虑如下场景，发送者希望将信息通过无线链路发送到接收者，而窃听者不能对保密信息译码，如上图所示，发送信号通过无线介质传播后被接收者和窃听者所接收，接收信号经历了路径损耗和加性噪声。假定发送者，接收者和窃听者分别有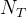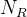![N_T](https://latex.csdn.net/eq?N_T)、![N_R](https://latex.csdn.net/eq?N_R)和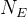![N_E](https://latex.csdn.net/eq?N_E)个天线，在时刻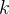![k](https://latex.csdn.net/eq?k)的发送-接收信道由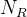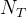![N_R](https://latex.csdn.net/eq?N_R)×![N_T](https://latex.csdn.net/eq?N_T)矩阵![\mathbf{H_k}](https://latex.csdn.net/eq?%5Cmathbf%7BH_k%7D)表示，矩阵![\mathbf{H_k}](https://latex.csdn.net/eq?%5Cmathbf%7BH_k%7D)的第j行表示第j个接收天线与发送天线之间的信道增益，，设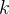![\textit{\textbf{x}}_k](https://latex.csdn.net/eq?%5Ctextit%7B%5Ctextbf%7Bx%7D%7D_k)和![\textit{\textbf{z}}_k](https://latex.csdn.net/eq?%5Ctextit%7B%5Ctextbf%7Bz%7D%7D_k)分别是时刻![k](https://latex.csdn.net/eq?k)的发送信号和接收信号，则接收信号表示为

其中，中各项是方差为的独立同分布加性循环对称复高斯白噪声。类似地，发送-窃听信道由×矩阵，窃听者接收到的信号表示为

其中，中各项是方差为的独立同分布加性循环对称复高斯白噪声。由分数疑义度来定义保密条件。当时可实现完美安全。保密容量定义为完美保密时保密信息发送到接收者的最大速率。