数学建模（学习记录）——层次分析法

准大二小白暑假准备高教杯，为了督促自己学习数学建模，来记录下学习情况。自己所学课程由清风老师讲解，文章末尾有其公众号及试听课地址。该课程主要讲解了十个模型，并讲解了相应的常用算法。

————————————————————————————————————————————————————————————

数学建模之评价类模型

评价类模型应该是最基础的模型之一了，往往对应着生活中一些很实际的问题。例如：A和B哪位员工的业绩更强、a1,a2,a3三个地方要去哪一个地方旅游......

想要解决评价类问题，首先要想到三个问题：

1.评价的目标是什么？2.为了达到此目标，有哪几种可选择的方案？3.评价的准则或者指标是什么（我们根据什么进行评价）？

注意：第三个问题一般题目不会指出，需要自行查找进行补充。

例：

高考完，小明出去旅游，初步选择了苏杭，北戴河，桂林三地之一作为目标景区。

请你确定评价指标，形成评价体系，为小明同学选择最佳方案。

答：
1.为小明选择最佳旅游景点；2.三种，分别为苏杭、北戴河、桂林；3.题目无相关数据支撑，需要自己确定。

三个问题已经分析完了，那么如何来对三个地方进行评价呢？

一个较好方法就是对三个地点分别进行打分。我们可以给予评价指标不同的权重，之后按照每个指标分别给三个地点打分，最后再加权求和，便可以给出三个地点比较合理的得分，作为我们评价的最终结果。之后便选择得分更高的那个景区作为目标景区去旅游。

据此，列出景色、花费、居住、饮食、交通五个常用指标。
指标权重苏杭北戴河桂林景色花费居住饮食交通
考虑到对于不同的评价问题存在不同的指标，其评价准则往往是不一样的，不一定都是以分数都是衡量标准。因此对于某个指标，给不同的方案进行打分时，我们依然以“权重”作为其衡量的标准，其权重之和为1即可。如上表格所示，相同颜色的单元格和为1，指标权重比较好理解，给予指标以不同的权重以加权。打分也是以“权重”来衡量，为了整体更方便计算，这里选择“权重”作为衡量的标准。

我目前接触到的解决评价类模型的方法有两种，分别是层析分析法以及TOPSIS法。其原理各有差别，但是大体上都是差不多的，也就是通过加权求和进行打分，最后选出最高分。区别便是不同的方法里，“分数”的表示不太相同。今天只讲层次分析法。

层次分析法

层次分析法，简称AHP，主要用于解决各种评价类问题。其适用对象往往是，不给出具体指标及指标权重，也不给出每一种方案在指标内部的权重。

如前文所提出的问题：小明想去旅游，有苏杭，北戴河，桂林三个城市可以选择，请确定评价指标，形成评价体系为小明选择最佳方案。

只给三个选择，没有指标和权重，这是层次分析法比较适合的题目类型。

遇到问题首先确定目标，选择旅游目的地，之后看看有哪些方案，再想想评价指标是什么？

对于没有给出评价指标的问题，我们可以结合生活常识，或者他人已经完成的研究来设定评价指标。

但采取生活常识远不如采取科学知识严谨，“科学知识”要比“常识”更经得起进一步观察和实验的检验，更倾向于准备接受别人的修正，具有更明确的适用条件，具有预见性和普遍性，并且显得十分专业。

这时候就要用的文献检索，发挥自己的搜商能力。在搜索相关文献时，建议采取知网、万方、百度学术、谷歌学术等专业网站进行检索。

若无相关文献，可采取小组内头脑风暴或平台上搜索别人或者专家的看法等方法。

对于同一个人来说，同时面对五个指标进行权重排序，由于指标较多，不同的时间点往往有不同的答案，今天我觉得是a，b，c，d，e，明天可能就觉得是e，d，c，b，a了。这就是为什么要用到层次分析法了。既然一次性考虑五个指标容易出现变化，且建模中凭感觉给数字也不太可靠，那我们就用一个比较科学又显得又水平的方法进行权重分配，也就是层次分析法。

层次分析法的思想如下：对于多个指标，我们可以两个两个进行比较评价，根据两两比较的结果来判断权重。为了进行量化，层次分析法使用了九个等级18个数字来比较两个指标之间的重要性（满意度）。

如下图。

如本例题，你询问小明：“小明小明，你觉得对于旅游景点而言，花费和景色哪个更重要？重要程度是多少？”利用重要程度进行量化，如果小明觉得，感觉花费比景色稍稍重要一点点，那花费对景色的标度就是2，景色对花费的标度就是1/2。

如此循环，两两比较，也就是10次询问，可得出相应将相应标度填在相应的表格中，得到一个对应的矩阵。

这个矩阵就是层次分析法中的判断矩阵。

小总结：上面这个矩阵是一个5*5的方阵，我们记为A，对应的元素为a ⁱ ʲ。

特点：（1）a ⁱ ʲ表示的意义是：与j相比i的重要程度。

       （2）当i=j时，两个指标相等，因此记为1，这也就是为什么主对角线的数值为1。

       （3）a ⁱ ʲ>0，且满足a ⁱ ʲ*a ʲ ⁱ=1，我们称此矩阵为正互反矩阵。

可因此得出每个元素的判断矩阵，如：

但这样一来可能会出现一些问题，如得出此类的判断矩阵：

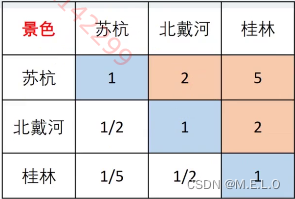
假设 苏杭=A，北戴河=B，桂林=C。

根据此表，苏杭比北戴河的景色稍好一点：A>B

              苏杭和桂林景色一样好：A=C

              北戴河比桂林景色好一点：B>C

可得，矛盾。

特此，引出一个概念，一致矩阵。

一致矩阵

满足以上条件即为一致矩阵 。如：

一致矩阵的特点：
各行（各列）成倍数关系。

小总结：

若矩阵中每个元素a ⁱ ʲ>0，且满足a ⁱ ʲ * a ʲ ⁱ=1，则我们称其为正互反矩阵。

在层次分析法中，我们构造的判断矩阵均是正互反矩阵。

若正互反矩阵满足a ⁱ ʲ * a ʲ ᵏ=a ⁱ ᵏ，则我们称该矩阵为一致矩阵。

注意：在使用判断矩阵求权重之前，应对其进行一致性检验。

如果一个判断矩阵是一致矩阵，那么我们应用层次分析法。因为在层次分析法的框架下，重要程度之间的比较满足理应满足这种关系，如果我们的判断矩阵刚好是一致矩阵，那我们对重要程度的衡量在形式上是十分准确的。但如果我们的判断矩阵最终和一致矩阵不同，那就说明我们在判断的过程中存在一定的偏差。因为我们的预期并不满足上述的乘法关系，我们往往凭感觉而不是数据进行判断。所以对于判断矩阵，我们也需要进行一定的检验，也就是一致性检验。一致性检验用来检测判断矩阵与一致矩阵的偏差度，如果偏差在接受范围内，那么我们可以接受这个判断矩阵作为我们心理预期的量化指标。如果偏差无法接受，那则说明，我们在层次分析法的框架下，对于心理预期的量化是失败的。如果还想运用层次分析法解题，就要重新判断了。

一致性检验：

目标：检验我们构造的判断矩阵和一致矩阵是否有太大的差别（线代知识）

（引理已跳过，直接上步骤）

一致性检验的步骤

1.计算一致性指标CI

CI = （λmax​−n）/（n-1）​,λmax:为最大特征值

2.查找对应的平均随机一致性指标RI，直接查表就好了

3.计算一致性比例CR

CR = CI/RI

之后就可以下判断了，如果CR<0.1，则认为判断矩阵的一致性可以接受，否则需要对判断矩阵进行修正，也就是尽量往一致矩阵去调整。

进行了一致性检验之后，我们可以计算各个指标的权重了。

怎么计算权重？

方法一：算术平均法求权重

1.一致矩阵

景色苏杭北戴河桂林苏杭124北戴河1/212桂林1/41/21
苏杭的重要性如果是1，那么北戴河为1/2，桂林为1/4.

注意：权重一定要进行归一化处理.

苏杭=1/(1+0.3+0.25)

北戴河=0.5/(1+0.3+0.25）

桂林+0.25/(1+0.3+0.25）

（判断矩阵为一致矩阵，那么根据每列算出来的权重是一样的，因为对应列，对应行，成比例）

2.判断矩阵

第一步：将判断矩阵按照归一化(每个元素除以所在列的和)
景色苏杭北戴河桂林苏杭0.58820.57140.625北戴河0.29410.28570.25桂林0.11770.41290.125
第二步：将归一化的各列相加(按行求和)
未归一化的权重苏杭0.5882+0.5714+0.625=1.7846北戴河0.2941+0.28857+0.25=0.8298桂林0.1177+0.1429+0.125=0.3856
第三步:将相加后得到的向量中每个元素除以n即可（n:个数）
苏杭1.7846/3=0.5949北戴河0.829813/3=0.2766桂林0.3856/3=0.1285

算术平均法具体三步：

方法二：几何平均法求权重

** 方法三：特征值法求权重**

至此，已用三种方法求出单一元素的权重。接下来是对其他五个元素三种方法进行求权重。

将其填入上文所列权重表中：

加权计算得分：

苏杭=0.26360.5954+0.47580.0819+0.05380.4286+0.09810.6337+0.1087*0.1667=0.2992

北戴河=0.26360.2764+0.47580.2363+0.05380.4286+0.09810.1919+0.1087*0.1667=0.2453

桂林=0.26360.1283+0.47580.6817+0.05380.1429+0.09810.1744+0.1087*0.1667=0.45545

所以，小明应选择桂林为目标景点。

本题结束。

总结

层次分析法的结构（逻辑）

1**.**分析系统中各因素的关系，建立系统层次结构

2.对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较，构造两两比较矩阵（判断矩阵）

1. 由判断矩阵计算被比较元素对于该准则的相对权重，并进行一致性检验，检验通过才可计算权重

4.根据权重矩阵计算得分，并进行排序，选择最佳选择或进行评价，判断。

局限性
判断矩阵阶数不能太多，上文中提到的RI，RI往往只给到n = 15，当需要比较的指标或者方案太多时，判断矩阵和一致矩阵差异往往会比较大。

本文根据清风老师的课程一以及个人听课收获写出，这里可以推荐一下清风老师的数学建模课，哔哩哔哩上数学建模试听课播放量最多的便是清风课程。可以关注相应的微信公众号“数学建模学习交流”。

bilibili链接：【强烈推荐】清风：数学建模算法、编程和写作培训的视频课程以及Matlab等软件教学_哔哩哔哩_bilibili

欢迎留言，欢迎给出写作意见，