超分之EDSR

这篇文章是SRResnet的升级版——EDSR，其对网络结构进行了优化(去除了BN层)，省下来的空间可以用于提升模型的size来增强表现力。此外，作者提出了一种基于EDSR且适用于多缩放尺度的超分结构——MDSR。

EDSR在2017年赢得了NTIRE2017超分辨率挑战赛的冠军。

参考目录：
①深度学习端到端超分辨率方法发展历程
②【图像超分辨】EDSR
③源码(Pytorch)
④源码(Facebook-torch)
⑤源码(Tensorflow)

Enhanced Deep Residual Networks for Single Image Super-Resolution

Abstract

1. 作者推出了一种加强版本的基于Resnet块的超分方法，它实际上是在SRResnet上的改进，去除了其中没必要的的BN部分，从而在节省下来的空间下扩展模型的size来增强表现力，它就是EDSR，其取得了当时SOAT的水平。
2. 此外，作者在文中还介绍了一种基于EDSR的多缩放尺度融合在一起的新结构——MDSR。
3. EDSR、MDSR在2017年分别赢得了NTIRE2017超分辨率挑战赛的冠军和亚军。
4. 此外，作者通过实验证明使用 L 1 − L o s s L1-Loss L1−Loss比 L 2 − L o s s L2-Loss L2−Loss具有更好的收敛特性。

1 Introduction

近几年来，深度学习在SR领域展现了较好的图像高分辨率重建表现，但是网络的结构上仍然存在着一些待优化的地方：

1. 深受神经网络的影响，SR网络在超参数(Hyper-parameters)、网络结构(Architecture)十分敏感。
2. 之前的算法(除了VDSR)总是为特定up-scale-factor而设计的SR网络，即scale-specific，将不同缩放尺度看成是互相独立的问题，因此我们需要一个统一的网络来处理不同缩放尺度的SR问题，比如 × 2 , 3 , 4 \times 2,3,4 ×2,3,4，这比训练3个不同缩放尺度的网络节省更多的资源消耗。

针对第一个网络结构问题，作者在SRResNet的基础上，对其网络中多余的BN层进行删除，从而节约了BN本身带来的存储消耗以及计算资源的消耗，相当于简化了网络结构。此外，选择一个合适的loss function，作者经过实验证明

    L
   
   
    1
   
   
    −
   
   
    L
   
   
    o
   
   
    s
   
   
    s
   
  
  
   L1-Loss
  
 
L1−Loss比

 
  
   
    L
   
   
    2
   
   
    −
   
   
    L
   
   
    o
   
   
    s
   
   
    s
   
  
  
   L2-Loss
  
 
L2−Loss具有更好的收敛特性。

Note：

1. MSE就是典型的 L 2 − L o s s L2-Loss L2−Loss。

针对第二个多缩放尺度问题，作者用2种不同的方式去处理：

1. 使用低缩放尺度( × 2 \times 2 ×2)训练之后的模型作为高缩放尺度的初始化参数，结果取得很好的表现，说明不同尺度之间是有内在相关联系的。
2. 作者设计以了一个可以结合多尺度的SR网络MDSR，除了网络的头部和尾部为各个缩放尺度独立之外，中间部分是共享网络。这种多尺度SR网络具有和单一缩放网络相近的表现力，且相比 n n n个单一网络， n n n个尺度相结合的MDSR消耗更少的资源。

EDSR和MDSR将在标准测试数据集上做测试，分别是Set5、Set14、B100、Urban100以及新的数据集DIV2K。结果显示两种算法在PSNR/SSIM上都取得了SOAT的表现，并在NTIRE2017超分大赛上包揽冠亚军。

2 Related Works

略

3 Proposed Methods

本节将正式开始介绍一种增强版本的SRResNet——

EDSR

(一种single-scale网络)，它通过移除了适合分类这种高级计算机视觉任务而不适合SR这种低级计算机视觉任务的BN层来减少计算资源损耗。
除此之外，本节还会介绍一种集合了多尺度于一个网络中的multi-scale超分网络——

MDSR

。

Note：

1. BN不适合超分任务的原因：点这里。

3.1 Residual blocks

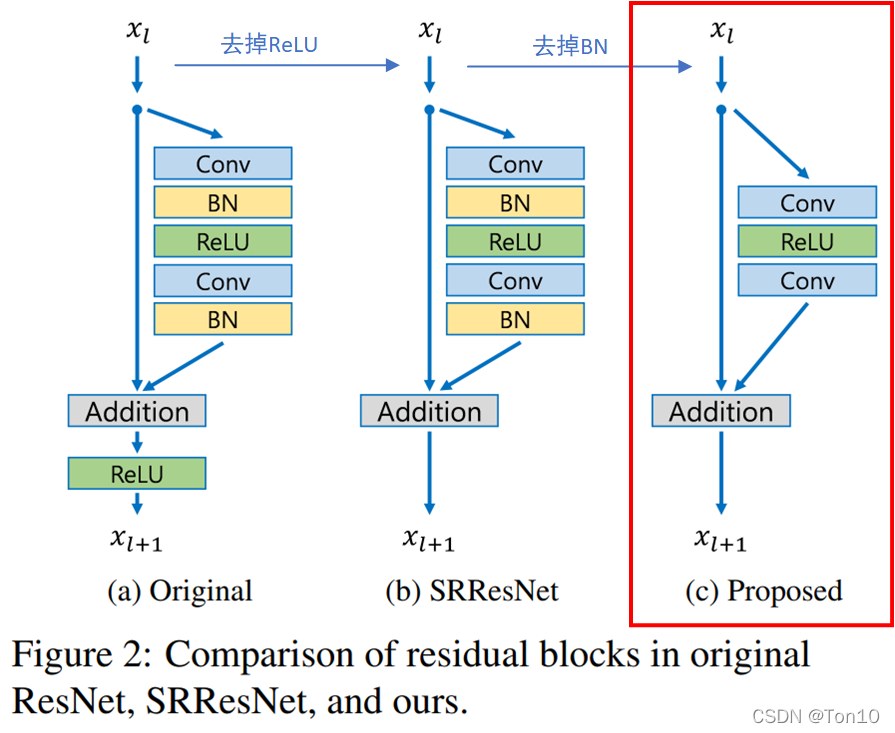
移除BN有以下三个好处：

1. 这样模型会更加轻量。BN层所消耗的存储空间等同于上一层CNN层所消耗的，作者指出相比于SRResNet，EDSR去掉BN层之后节约了 40 % 40% 40%的存储资源。
2. 在BN腾出来的空间下插入更多的类似于残差块等CNN-based子网络来增加模型的表现力。
3. BN层天然会拉伸图像本身的色彩、对比度，这样反倒会使得输出图像会变坏，实验也证明去掉BN层反倒可以增加模型的表现力。

3.2 Single-scale model

EDSR是SRResNet的增强版本，是一种基于上图红框所示的残差块。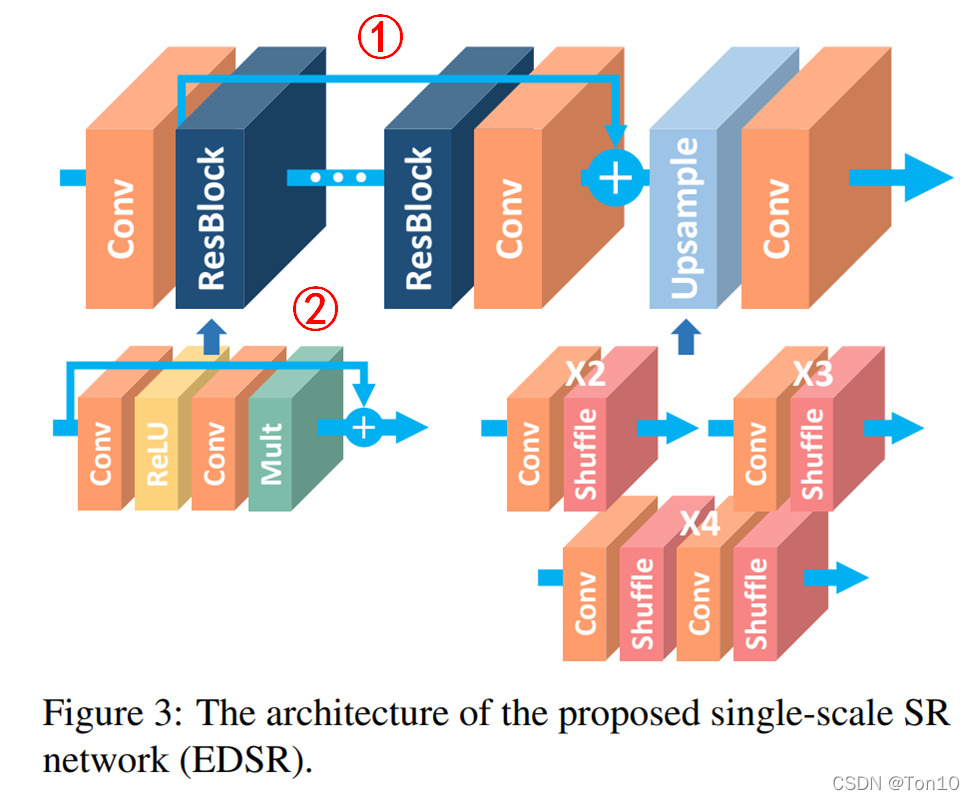
如上图所示就是EDSR的结构：最上面一排是网络结构，可以大致分为低层特征信息提取、高层特征信息提取、反卷积(上采样)层、重建层，基本和SRResNet、SRDenseNet是类似的。下面第二层分别表示残差块的构造以及反卷积层(分别是

    ×
   
   
    2
   
   
    、
   
   
    ×
   
   
    3
   
   
    、
   
   
    ×
   
   
    4
   
  
  
   \times 2、\times 3、\times 4
  
 
×2、×3、×4)的构造。

Note：

1. 连接①是将不同level的特征信息进行合并；连接②是ResNet块内部的残差连接。
2. 在EDSR的baseline中，是没有residual scaling的，因为只是用到了64层feature map，相对通道数较低，几乎没有不稳定现象。但是在最后实验的EDSR中，作者是设置了residual scaling中的缩减系数为0.1，且 B = 32 , F = 256 B=32,F=256 B=32,F=256。

增加模型表现力最直接的方式就是增加模型的参数(复杂度)，一般可以通过增加模型层数

    B
   
  
  
   B
  
 
B(即网络深度)以及滤波器个数

 
  
   
    F
   
  
  
   F
  
 
F(即网络宽度或者说通道数)。此外两者对于存储资源的消耗大约是

 
  
   
    O
   
   
    (
   
   
    B
   
   
    F
   
   
    )
   
  
  
   O(BF)
  
 
O(BF)，增加的参数大约是

 
  
   
    O
   
   
    (
   
   
    B
   
   
    
     F
    
    
     2
    
   
   
    )
   
  
  
   O(BF^2)
  
 
O(BF2)，因此增加滤波器个数才能在有限存储空间下最大化参数个数。

在Inception-ResNet这篇文章以及本文中都指出，过大的滤波器个数(feature map个数，或者说通道数)会导致网络不稳定，最佳的解决办法不是降低学习率或者增加BN层，而是通过在残差块最后一层卷积后加上Residual scaling层：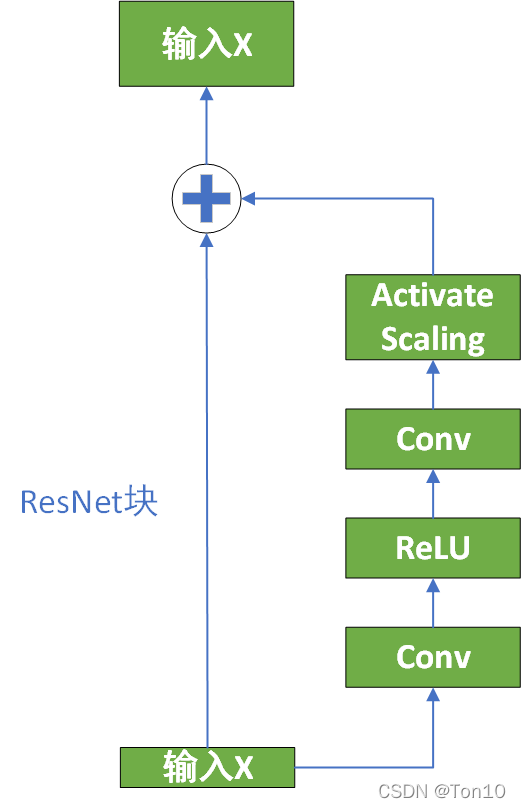

3.3 Multi-scale model

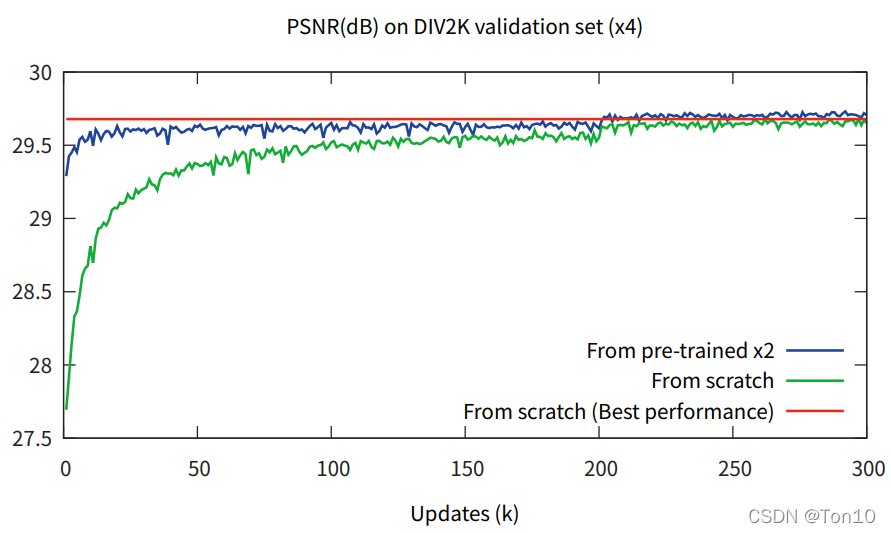
上图蓝色线表示的用训练好的up-scale-factor=2的EDSR网络作为

    ×
   
   
    3
   
   
    ,
   
   
    4
   
  
  
   \times 3,4
  
 
×3,4训练时候的初始化参数，结果来看收敛速度以及表现力的提升都是有目共睹的，这一定程度上说明了不同缩放尺度之间是存在某种内在联系的。

因此作者设计了一种在单一网络中实现多尺度融合的SR网络——MDSR，其结构如下：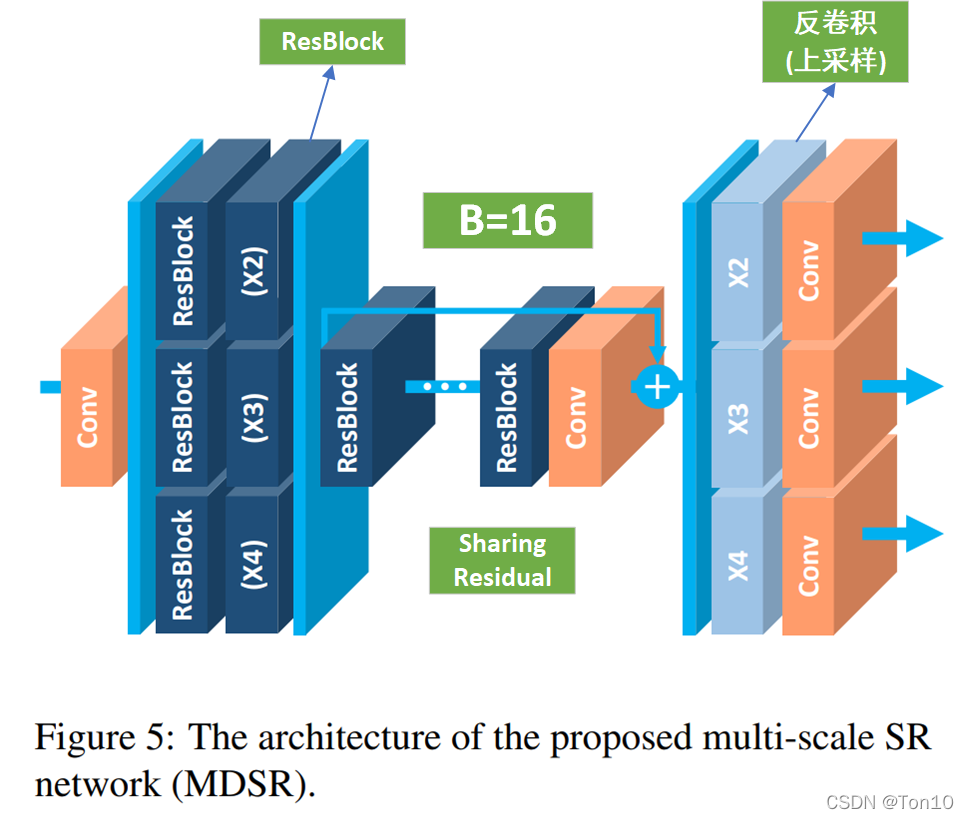

如上图所示是MDSR的网络结构，每个预处理模块由2个

    5
   
   
    ×
   
   
    5
   
  
  
   5\times 5
  
 
5×5的卷积层组成，针对每一种up-scale-factor设置不同的残差快；中间是一个共享残差网络；尾巴处是针对不同缩放倍数设计的上采样网络：![在这里插入图片描述](https://img-blog.csdnimg.cn/99d82ae74111445aa2499ba730a4823a.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAVG9uMTA=,size_20,color_FFFFFF,t_70,g_se,x_16)

Note：

1. 总体来说，MDSR是基于EDSR的结构。
2. 预处理阶段的残差块中的卷积采用较大的 5 × 5 5\times 5 5×5卷积核来增大初始阶段的感受野。
3. 作者统计了一笔数据，训练3个单独的EDSR-baseline来实现不同放大倍数的SR需要消耗 1.5 M ∗ 3 = 4.5 M 1.5M*3=4.5M 1.5M∗3=4.5M的参数量；而训练一个MDSR的baseline需要 3.2 M 3.2M 3.2M的参数量，而MDSR在后续实验中表现也还不错，因此MDSR是一种资源消耗相对少且有一定表现力的SR网络。

下表是SRResNet、EDSR、MDSR资源占用统计：

4 Experiments

4.1 Datasets

需要介绍一下新的数据集DIV2K，这是包含了2K高分辨率图像的数据集：训练集800张、验证集100张、测试集100张。
其余的标准benchmark：Set5、Set14、B100、Urban100。

4.2 Training Details

1. 输入是数据集中的patch部分，RGB格式的 48 × 48 48\times 48 48×48大小。
2. 通过水平翻转和90°旋转来做数据增强。
3. Adam做优化。
4. mini-batch=16。
5. 学习率从 1 0 − 4 10^{-4} 10−4开始，每过 2 × 1 0 5 2\times 10^5 2×105个epoches，就减半一次。
6. 对于EDSR中 × 3 、 4 \times 3、4 ×3、4的网络训练的初始化参数，是采用训练完毕的 × 2 \times 2 ×2EDSR网络的参数。而 × 2 \times 2 ×2的EDSR是从头开始训练的。
7. EDSR和MDSR都采用 L 1 − L o s s L1-Loss L1−Loss，作者通过大量实验表明L1比L2有更好的收敛特性。

4.3 Geometric Self-ensemble

几何自集成的方法用于在测试的时候，将每一张输入图像经过8种不同(其中一种是原图)的变换方式进行转换：

      I
     
     
      
       n
      
      
       ,
      
      
       i
      
     
     
      
       L
      
      
       R
      
     
    
    
     =
    
    
     
      T
     
     
      i
     
    
    
     (
    
    
     
      I
     
     
      n
     
     
      
       L
      
      
       R
      
     
    
    
     )
    
   
   
     I_{n,i}^{LR} = T_i(I_n^{LR}) 
   
  
 In,iLR​=Ti​(InLR​)然后将8个结果通过网络输出成

 
  
   
    {
   
   
    
     I
    
    
     
      n
     
     
      ,
     
     
      1
     
    
    
     
      S
     
     
      R
     
    
   
   
    ,
   
   
    
     I
    
    
     
      n
     
     
      ,
     
     
      2
     
    
    
     
      S
     
     
      R
     
    
   
   
    ⋯
    
   
    ,
   
   
    
     I
    
    
     
      n
     
     
      ,
     
     
      8
     
    
    
     
      S
     
     
      R
     
    
   
   
    }
   
  
  
   \{I^{SR}_{n,1},I^{SR}_{n,2}\cdots, I^{SR}_{n,8}\}
  
 
{In,1SR​,In,2SR​⋯,In,8SR​}，然后将每一个值经过转置处理：

 
  
   
    
     
      
       I
      
      
       ~
      
     
     
      
       n
      
      
       ,
      
      
       i
      
     
     
      
       S
      
      
       R
      
     
    
    
     =
    
    
     
      T
     
     
      i
     
     
      
       −
      
      
       1
      
     
    
    
     (
    
    
     
      I
     
     
      
       n
      
      
       ,
      
      
       i
      
     
     
      
       S
      
      
       R
      
     
    
    
     )
    
    
     ，
    
   
   
     \tilde{I}^{SR}_{n,i} = T_i^{-1}(I_{n,i}^{SR})， 
   
  
 I~n,iSR​=Ti−1​(In,iSR​)，最后在此基础上进行平均处理：

 
  
   
    
     
      I
     
     
      n
     
     
      
       S
      
      
       R
      
     
    
    
     =
    
    
     
      1
     
     
      8
     
    
    
     
      ∑
     
     
      
       i
      
      
       =
      
      
       1
      
     
     
      8
     
    
    
     
      
       I
      
      
       ~
      
     
     
      
       n
      
      
       ,
      
      
       i
      
     
     
      
       S
      
      
       R
      
     
    
    
     .
    
   
   
     I^{SR}_n = \frac{1}{8}\sum^8_{i=1}\tilde{I}^{SR}_{n,i}. 
   
  
 InSR​=81​i=1∑8​I~n,iSR​.最后拿着最终的结果去计算PSNR/SSIM，即图表中的EDSR+、MDSR+，从实验结果来看，self-ensemble确实可以提升表现力。

4.4 Evaluation on DIV2K Dataset

在DIV2K验证集(测试集不公开)中实验结果如下：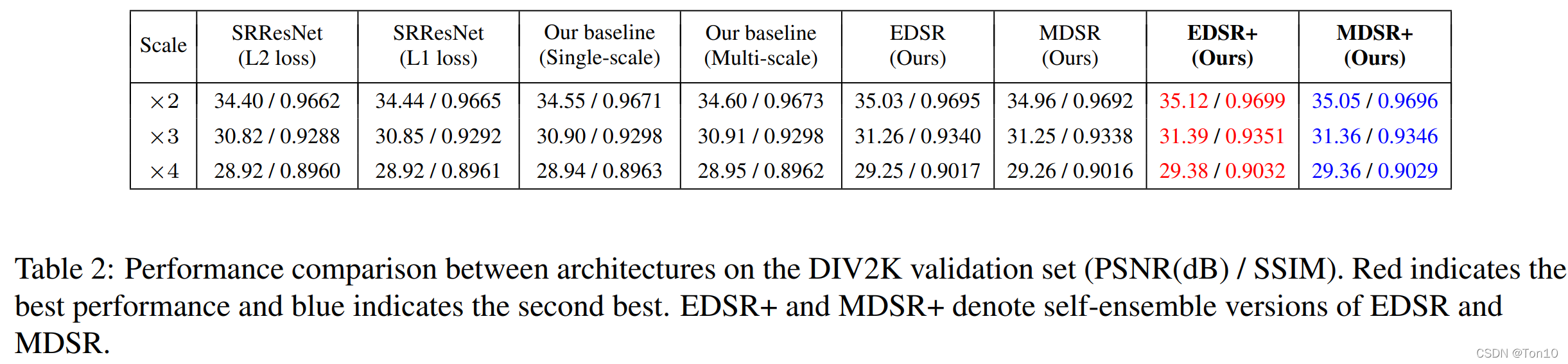

Note：

1. 从结果来看，L1比L2-Loss更能对表现力进行提升。
2. Geometric Self-ensemble确实可以提升表现力。
3. EDSR在DIV2K上获取最佳的表现，其次MDSR也表现尚可。

4.5 Benchmark Results

作者对多种SR算法在Benchmark上的表现进行统计，结果如下：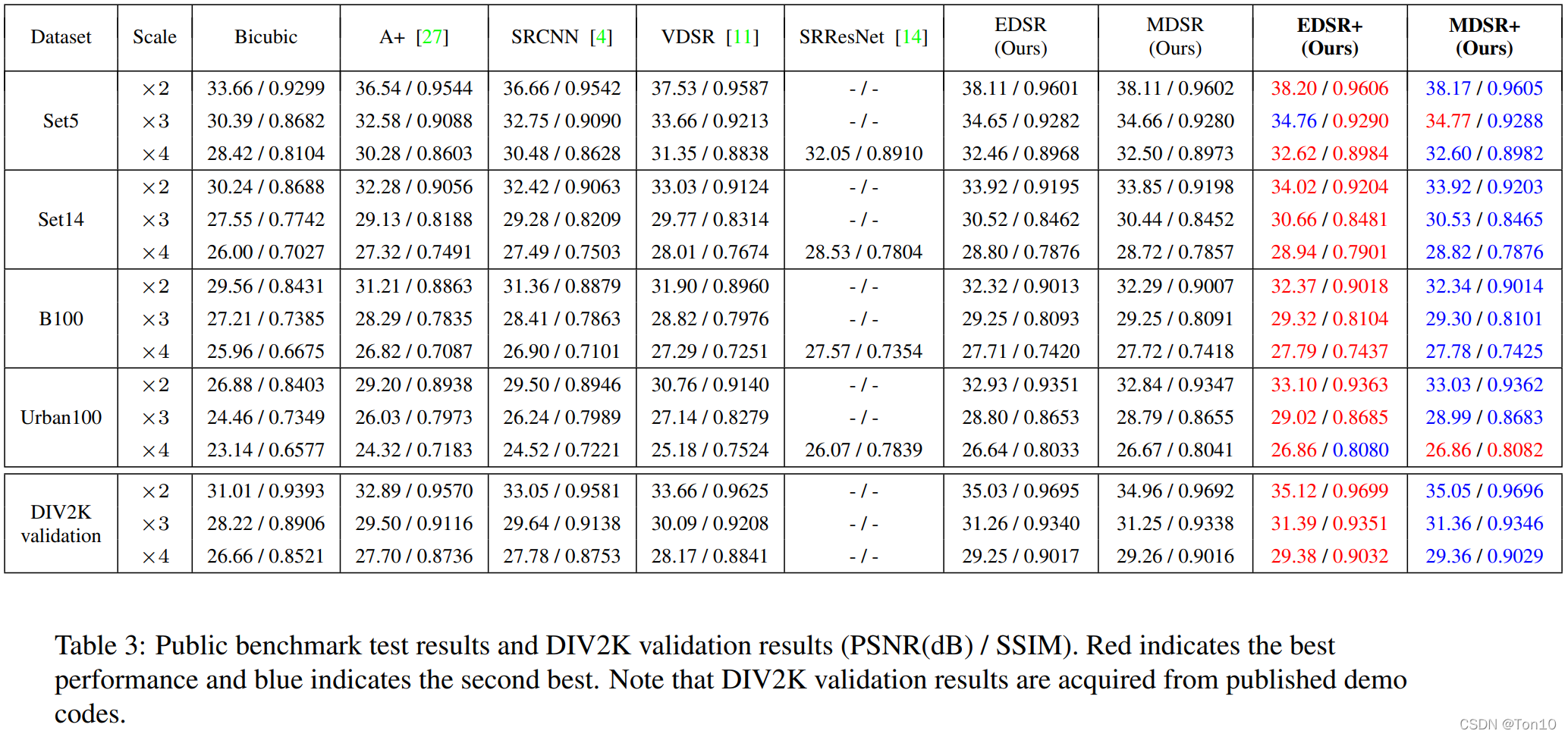

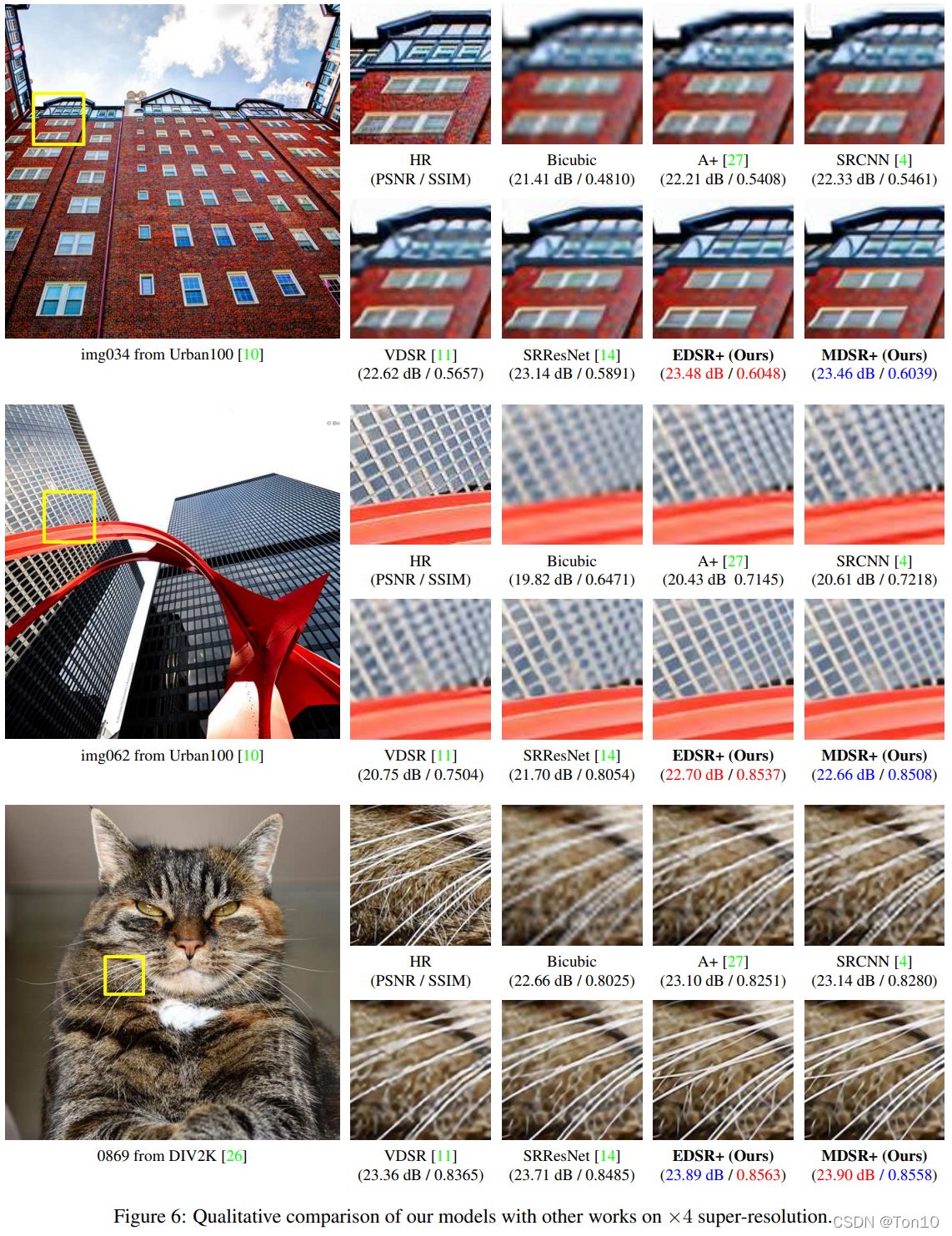
Note：

1. 总体来看，EDSR和MDSR是包揽了最佳和次佳的表现结果。
2. 从SRResNet和EDSR的对比来看，去除了BN层确实对表现力有提升效果。

5 NTIRE2017 SR Challenge

下面是EDSR和MDSR在NTIRE2017超分挑战赛上的表现，当时获取了第一和第二名的结果：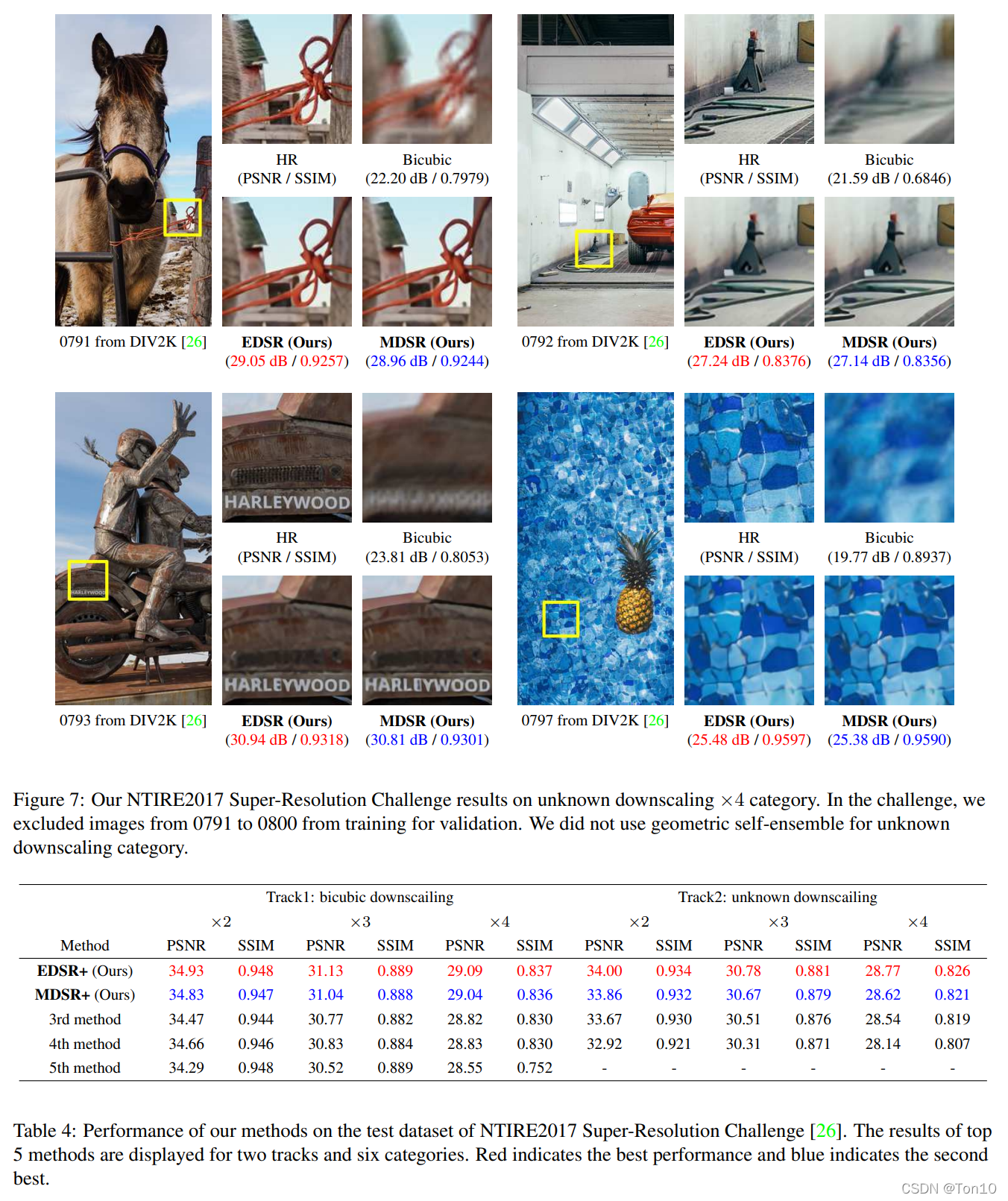

6 Conclusion

文章的贡献如下：

1. 提出了一种增强型SRResNet的scale-specific网络——EDSR，它以残差块为基础，移除了不适合SR任务的BN块，从而减轻网络以及增强了网络的表现力，同时也使得BN空出来的部分可以插进更多的CNN来进一步提升网络的拟合能力。
2. 为了减缓feature map过多(滤波器过多或者说通道数过大)带来训练不稳定的问题，作者借用Inception-ResNet那篇文章说的residual scaling技术加入到EDSR的残差块最后一层CNN后。
3. 提出了一种在单一网络中实现多尺度融合的SR网络——MDSR，包括 × 2 、 3 、 4 \times 2、3、4 ×2、3、4。相比训练3个不同单一尺度的SR网络，MDSR可以节省更多的参数。
4. 作者经过大量实验表明，L1-Loss比L2-Loss具有更好的收敛能力。