大家好,今天和各位分享一下如何使用** Pytorch 构建卷积神经网络中的各种注意力机制,如:SENet,ECANet,CBAM**。
注意力机制的原理 和 **TensorFlow2 **的实现方式可以看我下面两篇博文:
SENet、ECANet:https://blog.csdn.net/dgvv4/article/details/123572065
DANet、CBAM:https://blog.csdn.net/dgvv4/article/details/123888724
1. SENet
1.1 方法介绍
SE注意力机制(Squeeze-and-Excitation Networks)在通道维度增加注意力机制,关键操作是squeeze和excitation。
通过自动学习的方式,使用另外一个新的神经网络,获取到特征图的每个通道的重要程度,然后用这个重要程度去给每个特征赋予一个权重值,从而让神经网络重点关注某些特征通道。提升对当前任务有用的特征图的通道,并抑制对当前任务用处不大的特征通道。
如下图所示,在输入SE注意力机制之前(左侧图C),特征图的每个通道的重要程度都是一样的,通过SENet之后(右侧彩图C),不同颜色代表不同的权重,使每个特征通道的重要性变得不一样了,使神经网络重点关注某些权重值大的通道。
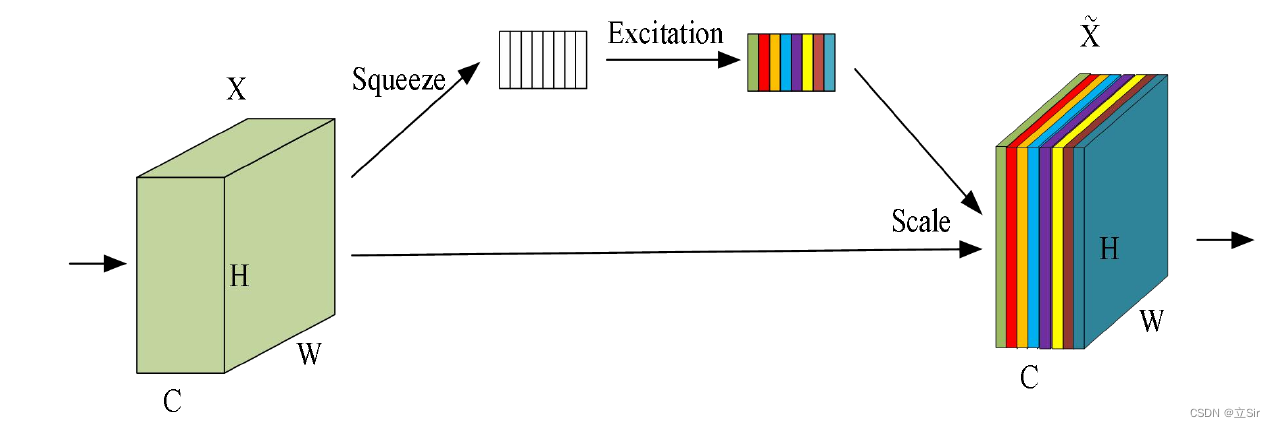
SE注意力机制的实现步骤如下:
(1)****Squeeze:通过全局平均池化,将每个通道的二维特征(H*W)压缩为1个实数,将特征图从 [h, w, c] ==> [1,1,c]
(2)****excitation:给每个特征通道生成一个权重值,论文中通过两个全连接层构建通道间的相关性,输出的权重值数目和输入特征图的通道数相同。[1,1,c] ==> [1,1,c]
(3)****Scale:将前面得到的归一化权重加权到每个通道的特征上。论文中使用的是乘法,逐通道乘以权重系数。[h,w,c]*[1,1,c] ==> [h,w,c]
小节:
(1)SENet的核心思想是通过全连接网络根据loss损失来自动学习特征权重,而不是直接根据特征通道的数值分配来判断,使有效的特征通道的权重大。当然SE注意力机制不可避免的增加了一些参数和计算量,但性价比还是挺高的。
(2)论文认为excitation操作中使用两个全连接层相比直接使用一个全连接层,它的好处在于,具有更多的非线性,可以更好地拟合通道间的复杂关联。
1.2 代码实现
SE注意力机制代码如下:
# -------------------------------------------- #
#(1)SE 通道注意力机制
# -------------------------------------------- #
import torch
from torch import nn
from torchstat import stat # 查看网络参数
# 定义SE注意力机制的类
class se_block(nn.Module):
# 初始化, in_channel代表输入特征图的通道数, ratio代表第一个全连接下降通道的倍数
def __init__(self, in_channel, ratio=4):
# 继承父类初始化方法
super(se_block, self).__init__()
# 属性分配
# 全局平均池化,输出的特征图的宽高=1
self.avg_pool = nn.AdaptiveAvgPool2d(output_size=1)
# 第一个全连接层将特征图的通道数下降4倍
self.fc1 = nn.Linear(in_features=in_channel, out_features=in_channel//ratio, bias=False)
# relu激活
self.relu = nn.ReLU()
# 第二个全连接层恢复通道数
self.fc2 = nn.Linear(in_features=in_channel//ratio, out_features=in_channel, bias=False)
# sigmoid激活函数,将权值归一化到0-1
self.sigmoid = nn.Sigmoid()
# 前向传播
def forward(self, inputs): # inputs 代表输入特征图
# 获取输入特征图的shape
b, c, h, w = inputs.shape
# 全局平均池化 [b,c,h,w]==>[b,c,1,1]
x = self.avg_pool(inputs)
# 维度调整 [b,c,1,1]==>[b,c]
x = x.view([b,c])
# 第一个全连接下降通道 [b,c]==>[b,c//4]
x = self.fc1(x)
x = self.relu(x)
# 第二个全连接上升通道 [b,c//4]==>[b,c]
x = self.fc2(x)
# 对通道权重归一化处理
x = self.sigmoid(x)
# 调整维度 [b,c]==>[b,c,1,1]
x = x.view([b,c,1,1])
# 将输入特征图和通道权重相乘
outputs = x * inputs
return outputs
构造输入层,查看一次前向传播的输出结果,打印网络结构
# 构造输入层shape==[4,32,16,16]
inputs = torch.rand(4,32,16,16)
# 获取输入通道数
in_channel = inputs.shape[1]
# 模型实例化
model = se_block(in_channel=in_channel)
# 前向传播查看输出结果
outputs = model(inputs)
print(outputs.shape) # [4,32,16,16])
print(model) # 查看模型结构
stat(model, input_size=[32,16,16]) # 查看参数,不需要指定batch维度
网络的参数量如下:
module name input shape output shape params memory(MB) MAdd Flops MemRead(B) MemWrite(B) duration[%] MemR+W(B)
0 avg_pool 32 16 16 32 1 1 0.0 0.00 0.0 0.0 0.0 0.0 99.99% 0.0
1 fc1 32 8 256.0 0.00 504.0 256.0 1152.0 32.0 0.00% 1184.0
2 relu 8 8 0.0 0.00 8.0 8.0 32.0 32.0 0.00% 64.0
3 fc2 8 32 256.0 0.00 480.0 256.0 1056.0 128.0 0.00% 1184.0
4 sigmoid 32 32 0.0 0.00 0.0 0.0 0.0 0.0 0.00% 0.0
total 512.0 0.00 992.0 520.0 0.0 0.0 99.99% 2432.0
============================================================================================================================
Total params: 512
----------------------------------------------------------------------------------------------------------------------------
Total memory: 0.00MB
Total MAdd: 992MAdd
Total Flops: 520Flops
Total MemR+W: 2.38KB
2. ECANet
2.1 方法介绍
ECANet 是通道注意力机制的一种实现形式,ECANet 可以看做是 SENet 的改进版。
作者表明 SENet 中的降维会给通道注意力机制带来副作用,并且捕获所有通道之间的依存关系是效率不高的,而且是不必要的。
ECA 注意力机制模块****直接在全局平均池化层之后使用1x1卷积层,去除了全连接层。该模块避免了维度缩减,并有效捕获了跨通道交互。并且 ECANet 只涉及少数参数就能达到很好的效果。
ECANet **通过 ****一维卷积 layers.Conv1D **来完成跨通道间的信息交互,卷积核的大小通过一个函数来自适应变化,使得通道数较大的层可以更多地进行跨通道交互。
自适应函数为: ,其中
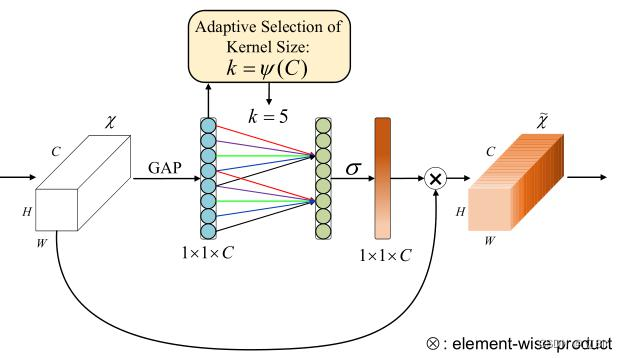
ECA注意力机制的实现过程如下:
(1)将输入特征图经过全局平均池化,特征图从 [h,w,c] 的矩阵变成 [1,1,c] 的向量
(2)根据特征图的通道数计算得到自适应的一维卷积核大小 kernel_size
(3)将 kernel_size 用于一维卷积中,得到对于特征图的每个通道的权重
(4)将归一化权重和原输入特征图逐通道相乘,生成加权后的特征图
2.2 代码展示
ECA注意力机制的代码如下:
# --------------------------------------------------------- #
#(2)ECANet 通道注意力机制
# 使用1D卷积代替SE注意力机制中的全连接层
# --------------------------------------------------------- #
import torch
from torch import nn
import math
from torchstat import stat # 查看网络参数
# 定义ECANet的类
class eca_block(nn.Module):
# 初始化, in_channel代表特征图的输入通道数, b和gama代表公式中的两个系数
def __init__(self, in_channel, b=1, gama=2):
# 继承父类初始化
super(eca_block, self).__init__()
# 根据输入通道数自适应调整卷积核大小
kernel_size = int(abs((math.log(in_channel, 2)+b)/gama))
# 如果卷积核大小是奇数,就使用它
if kernel_size % 2:
kernel_size = kernel_size
# 如果卷积核大小是偶数,就把它变成奇数
else:
kernel_size = kernel_size
# 卷积时,为例保证卷积前后的size不变,需要0填充的数量
padding = kernel_size // 2
# 全局平均池化,输出的特征图的宽高=1
self.avg_pool = nn.AdaptiveAvgPool2d(output_size=1)
# 1D卷积,输入和输出通道数都=1,卷积核大小是自适应的
self.conv = nn.Conv1d(in_channels=1, out_channels=1, kernel_size=kernel_size,
bias=False, padding=padding)
# sigmoid激活函数,权值归一化
self.sigmoid = nn.Sigmoid()
# 前向传播
def forward(self, inputs):
# 获得输入图像的shape
b, c, h, w = inputs.shape
# 全局平均池化 [b,c,h,w]==>[b,c,1,1]
x = self.avg_pool(inputs)
# 维度调整,变成序列形式 [b,c,1,1]==>[b,1,c]
x = x.view([b,1,c])
# 1D卷积 [b,1,c]==>[b,1,c]
x = self.conv(x)
# 权值归一化
x = self.sigmoid(x)
# 维度调整 [b,1,c]==>[b,c,1,1]
x = x.view([b,c,1,1])
# 将输入特征图和通道权重相乘[b,c,h,w]*[b,c,1,1]==>[b,c,h,w]
outputs = x * inputs
return outputs
构造输入层,查看一次前向传播的输出结果,打印网络结构
# 构造输入层 [b,c,h,w]==[4,32,16,16]
inputs = torch.rand([4,32,16,16])
# 获取输入图像的通道数
in_channel = inputs.shape[1]
# 模型实例化
model = eca_block(in_channel=in_channel)
# 前向传播
outputs = model(inputs)
print(outputs.shape) # 查看输出结果
print(model) # 查看网络结构
stat(model, input_size=[32,16,16]) # 查看网络参数
网络的参数量如下:
module name input shape output shape params memory(MB) MAdd Flops MemRead(B) MemWrite(B) duration[%] MemR+W(B)
0 avg_pool 32 16 16 32 1 1 0.0 0.00 0.0 0.0 0.0 0.0 0.00% 0.0
1 conv 1 32 1 32 3.0 0.00 0.0 0.0 0.0 0.0 0.00% 0.0
2 sigmoid 1 32 1 32 0.0 0.00 0.0 0.0 0.0 0.0 0.00% 0.0
total 3.0 0.00 0.0 0.0 0.0 0.0 0.00% 0.0
=========================================================================================================================
Total params: 3
-------------------------------------------------------------------------------------------------------------------------
Total memory: 0.00MB
Total MAdd: 0MAdd
Total Flops: 0Flops
Total MemR+W: 0B
3. CBAM 注意力机制
3.1 方法介绍
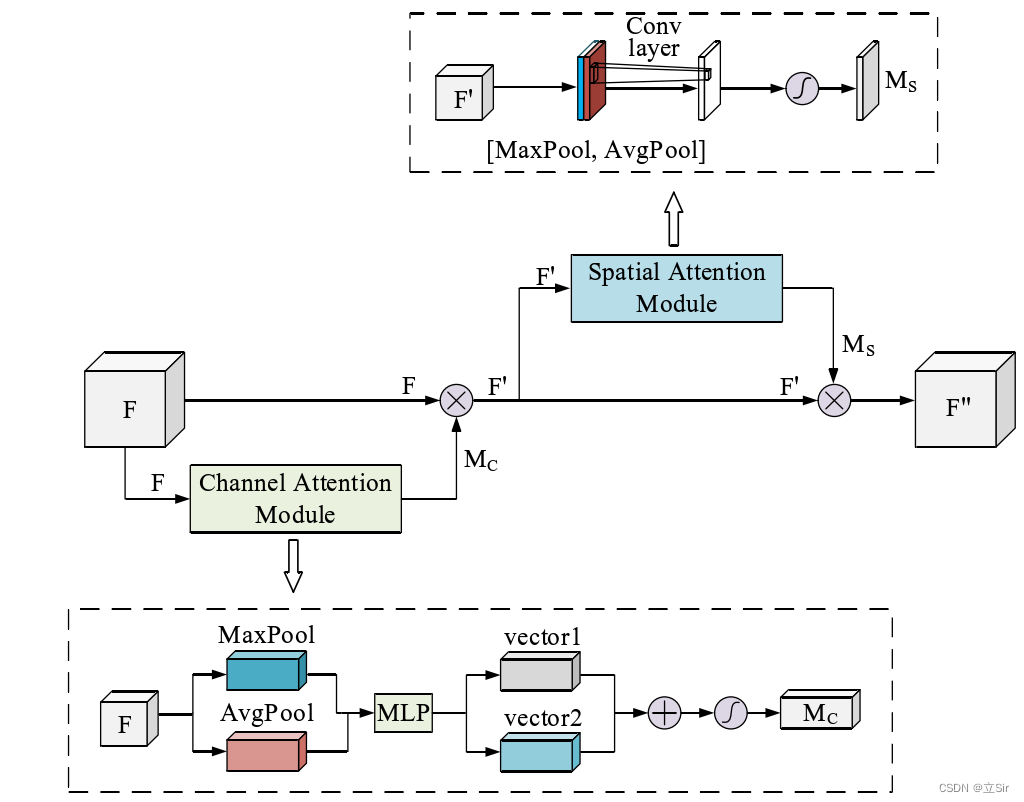
CBAM注意力机制是由通道注意力机制(channel)和空间注意力机制(spatial)组成。
传统基于卷积神经网络的注意力机制更多的是关注对通道域的分析,局限于考虑特征图通道之间的作用关系。CBAM从 channel 和 spatial 两个作用域出发,引入空间注意力和通道注意力两个分析维度,实现从通道到空间的顺序注意力结构。空间注意力可使神经网络更加关注图像中对分类起决定作用的像素区域而忽略无关紧要的区域,通道注意力则用于处理特征图通道的分配关系,同时对两个维度进行注意力分配增强了注意力机制对模型性能的提升效果。
3.2 通道注意力机制模块
CBAM中的通道注意力机制模块流程图如下。先将输入特征图分别进行全局最大池化和全局平均池化,对特征映射基于两个维度压缩,获得两张不同维度的特征描述。池化后的特征图共用一个多层感知器网络,先通过一个全连接层下降通道数,再通过另一个全连接恢复通道数。将两张特征图在通道维度堆叠,经过 sigmoid 激活函数将特征图的每个通道的权重归一化到0-1之间。将归一化后的权重和输入特征图相乘。
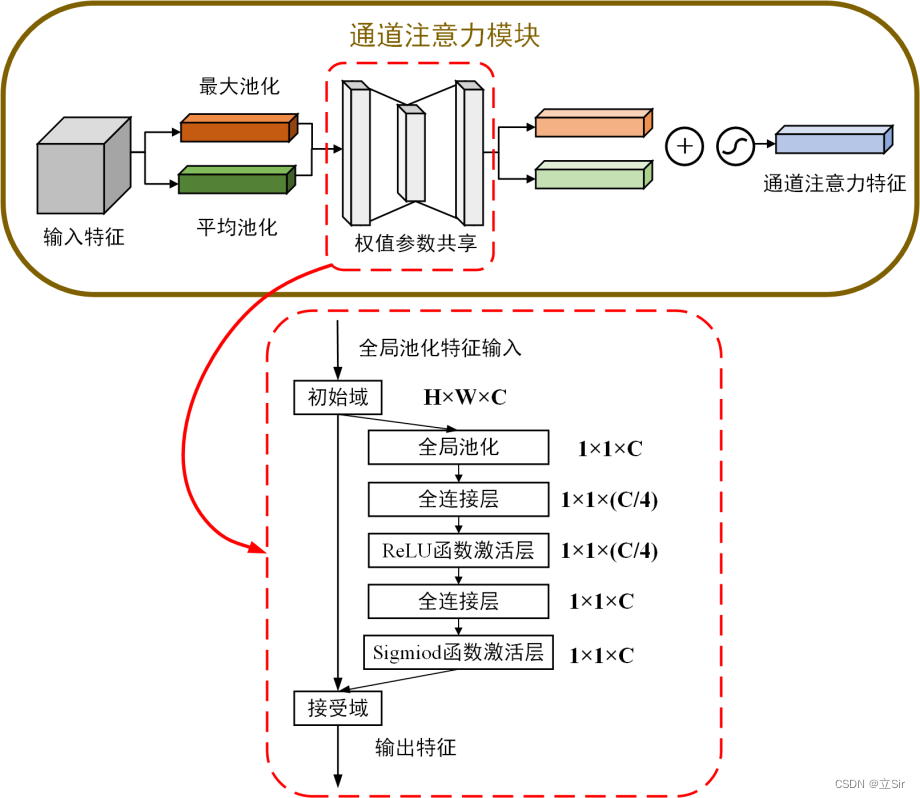
代码展示:
#(1)通道注意力机制
class channel_attention(nn.Module):
# 初始化, in_channel代表输入特征图的通道数, ratio代表第一个全连接的通道下降倍数
def __init__(self, in_channel, ratio=4):
# 继承父类初始化方法
super(channel_attention, self).__init__()
# 全局最大池化 [b,c,h,w]==>[b,c,1,1]
self.max_pool = nn.AdaptiveMaxPool2d(output_size=1)
# 全局平均池化 [b,c,h,w]==>[b,c,1,1]
self.avg_pool = nn.AdaptiveAvgPool2d(output_size=1)
# 第一个全连接层, 通道数下降4倍
self.fc1 = nn.Linear(in_features=in_channel, out_features=in_channel//ratio, bias=False)
# 第二个全连接层, 恢复通道数
self.fc2 = nn.Linear(in_features=in_channel//ratio, out_features=in_channel, bias=False)
# relu激活函数
self.relu = nn.ReLU()
# sigmoid激活函数
self.sigmoid = nn.Sigmoid()
# 前向传播
def forward(self, inputs):
# 获取输入特征图的shape
b, c, h, w = inputs.shape
# 输入图像做全局最大池化 [b,c,h,w]==>[b,c,1,1]
max_pool = self.max_pool(inputs)
# 输入图像的全局平均池化 [b,c,h,w]==>[b,c,1,1]
avg_pool = self.avg_pool(inputs)
# 调整池化结果的维度 [b,c,1,1]==>[b,c]
max_pool = max_pool.view([b,c])
avg_pool = avg_pool.view([b,c])
# 第一个全连接层下降通道数 [b,c]==>[b,c//4]
x_maxpool = self.fc1(max_pool)
x_avgpool = self.fc1(avg_pool)
# 激活函数
x_maxpool = self.relu(x_maxpool)
x_avgpool = self.relu(x_avgpool)
# 第二个全连接层恢复通道数 [b,c//4]==>[b,c]
x_maxpool = self.fc2(x_maxpool)
x_avgpool = self.fc2(x_avgpool)
# 将这两种池化结果相加 [b,c]==>[b,c]
x = x_maxpool + x_avgpool
# sigmoid函数权值归一化
x = self.sigmoid(x)
# 调整维度 [b,c]==>[b,c,1,1]
x = x.view([b,c,1,1])
# 输入特征图和通道权重相乘 [b,c,h,w]
outputs = inputs * x
return outputs
3.3 空间注意力机制模块
CBAM中的空间注意力机制模块如下。对通道注意力机制的输出特征图进行空间域的处理。首先,对输入特征图在通道维度下做最大池化和平均池化,将池化后的两张特征图在通道维度堆叠。然后,使用 77 (或33、1*1)大小的卷积核融合通道信息,特征图的shape从 [b,2,h,w] 变成 [b,1,h,w]。最后,将卷积后的结果经过 sigmoid 函数对特征图的空间权重归一化,再将输入特征图和权重相乘。
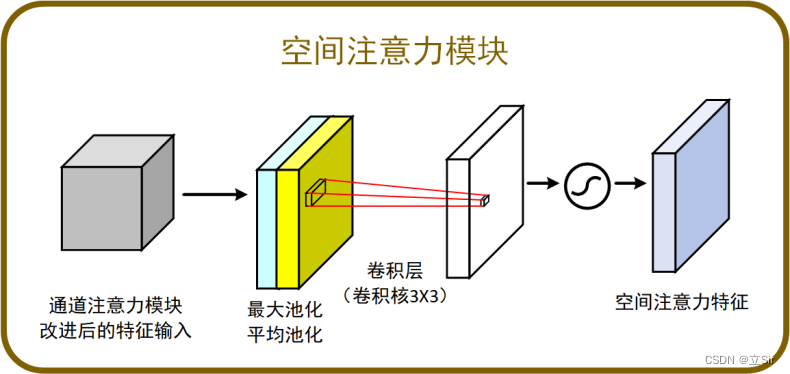
代码展示:
#(2)空间注意力机制
class spatial_attention(nn.Module):
# 初始化,卷积核大小为7*7
def __init__(self, kernel_size=7):
# 继承父类初始化方法
super(spatial_attention, self).__init__()
# 为了保持卷积前后的特征图shape相同,卷积时需要padding
padding = kernel_size // 2
# 7*7卷积融合通道信息 [b,2,h,w]==>[b,1,h,w]
self.conv = nn.Conv2d(in_channels=2, out_channels=1, kernel_size=kernel_size,
padding=padding, bias=False)
# sigmoid函数
self.sigmoid = nn.Sigmoid()
# 前向传播
def forward(self, inputs):
# 在通道维度上最大池化 [b,1,h,w] keepdim保留原有深度
# 返回值是在某维度的最大值和对应的索引
x_maxpool, _ = torch.max(inputs, dim=1, keepdim=True)
# 在通道维度上平均池化 [b,1,h,w]
x_avgpool = torch.mean(inputs, dim=1, keepdim=True)
# 池化后的结果在通道维度上堆叠 [b,2,h,w]
x = torch.cat([x_maxpool, x_avgpool], dim=1)
# 卷积融合通道信息 [b,2,h,w]==>[b,1,h,w]
x = self.conv(x)
# 空间权重归一化
x = self.sigmoid(x)
# 输入特征图和空间权重相乘
outputs = inputs * x
return outputs
3.4 CBAM注意力机制
CBAM的总体流程图如下。输入特征图先经过通道注意力机制,将通道权重和输入特征图相乘后再送入空间注意力机制,将归一化后的空间权重和空间注意力机制的输入特征图相乘,得到最终加权后的特征图。
完整代码展示:
# ---------------------------------------------------- #
# CBAM注意力机制
# 结合了通道注意力机制和空间注意力机制
# ---------------------------------------------------- #
import torch
from torch import nn
from torchstat import stat # 查看网络参数
#(1)通道注意力机制
class channel_attention(nn.Module):
# 初始化, in_channel代表输入特征图的通道数, ratio代表第一个全连接的通道下降倍数
def __init__(self, in_channel, ratio=4):
# 继承父类初始化方法
super(channel_attention, self).__init__()
# 全局最大池化 [b,c,h,w]==>[b,c,1,1]
self.max_pool = nn.AdaptiveMaxPool2d(output_size=1)
# 全局平均池化 [b,c,h,w]==>[b,c,1,1]
self.avg_pool = nn.AdaptiveAvgPool2d(output_size=1)
# 第一个全连接层, 通道数下降4倍
self.fc1 = nn.Linear(in_features=in_channel, out_features=in_channel//ratio, bias=False)
# 第二个全连接层, 恢复通道数
self.fc2 = nn.Linear(in_features=in_channel//ratio, out_features=in_channel, bias=False)
# relu激活函数
self.relu = nn.ReLU()
# sigmoid激活函数
self.sigmoid = nn.Sigmoid()
# 前向传播
def forward(self, inputs):
# 获取输入特征图的shape
b, c, h, w = inputs.shape
# 输入图像做全局最大池化 [b,c,h,w]==>[b,c,1,1]
max_pool = self.max_pool(inputs)
# 输入图像的全局平均池化 [b,c,h,w]==>[b,c,1,1]
avg_pool = self.avg_pool(inputs)
# 调整池化结果的维度 [b,c,1,1]==>[b,c]
max_pool = max_pool.view([b,c])
avg_pool = avg_pool.view([b,c])
# 第一个全连接层下降通道数 [b,c]==>[b,c//4]
x_maxpool = self.fc1(max_pool)
x_avgpool = self.fc1(avg_pool)
# 激活函数
x_maxpool = self.relu(x_maxpool)
x_avgpool = self.relu(x_avgpool)
# 第二个全连接层恢复通道数 [b,c//4]==>[b,c]
x_maxpool = self.fc2(x_maxpool)
x_avgpool = self.fc2(x_avgpool)
# 将这两种池化结果相加 [b,c]==>[b,c]
x = x_maxpool + x_avgpool
# sigmoid函数权值归一化
x = self.sigmoid(x)
# 调整维度 [b,c]==>[b,c,1,1]
x = x.view([b,c,1,1])
# 输入特征图和通道权重相乘 [b,c,h,w]
outputs = inputs * x
return outputs
# ---------------------------------------------------- #
#(2)空间注意力机制
class spatial_attention(nn.Module):
# 初始化,卷积核大小为7*7
def __init__(self, kernel_size=7):
# 继承父类初始化方法
super(spatial_attention, self).__init__()
# 为了保持卷积前后的特征图shape相同,卷积时需要padding
padding = kernel_size // 2
# 7*7卷积融合通道信息 [b,2,h,w]==>[b,1,h,w]
self.conv = nn.Conv2d(in_channels=2, out_channels=1, kernel_size=kernel_size,
padding=padding, bias=False)
# sigmoid函数
self.sigmoid = nn.Sigmoid()
# 前向传播
def forward(self, inputs):
# 在通道维度上最大池化 [b,1,h,w] keepdim保留原有深度
# 返回值是在某维度的最大值和对应的索引
x_maxpool, _ = torch.max(inputs, dim=1, keepdim=True)
# 在通道维度上平均池化 [b,1,h,w]
x_avgpool = torch.mean(inputs, dim=1, keepdim=True)
# 池化后的结果在通道维度上堆叠 [b,2,h,w]
x = torch.cat([x_maxpool, x_avgpool], dim=1)
# 卷积融合通道信息 [b,2,h,w]==>[b,1,h,w]
x = self.conv(x)
# 空间权重归一化
x = self.sigmoid(x)
# 输入特征图和空间权重相乘
outputs = inputs * x
return outputs
# ---------------------------------------------------- #
#(3)CBAM注意力机制
class cbam(nn.Module):
# 初始化,in_channel和ratio=4代表通道注意力机制的输入通道数和第一个全连接下降的通道数
# kernel_size代表空间注意力机制的卷积核大小
def __init__(self, in_channel, ratio=4, kernel_size=7):
# 继承父类初始化方法
super(cbam, self).__init__()
# 实例化通道注意力机制
self.channel_attention = channel_attention(in_channel=in_channel, ratio=ratio)
# 实例化空间注意力机制
self.spatial_attention = spatial_attention(kernel_size=kernel_size)
# 前向传播
def forward(self, inputs):
# 先将输入图像经过通道注意力机制
x = self.channel_attention(inputs)
# 然后经过空间注意力机制
x = self.spatial_attention(x)
return x
3.5 查看网络结构
构造输入层,查看一次前向传播的输出结果,打印网络结构
# 构造输入层 [b,c,h,w]==[4,32,16,16]
inputs = torch.rand([4,32,16,16])
# 获取输入图像的通道数
in_channel = inputs.shape[1]
# 模型实例化
model = cbam(in_channel=in_channel)
# 前向传播
outputs = model(inputs)
print(outputs.shape) # 查看输出结果
print(model) # 查看网络结构
stat(model, input_size=[32,16,16]) # 查看网络参数
查看模型参数量
module name input shape output shape params memory(MB) MAdd Flops MemRead(B) MemWrite(B) duration[%] MemR+W(B)
0 channel_attention.max_pool 32 16 16 32 1 1 0.0 0.00 0.0 0.0 0.0 0.0 0.00% 0.0
1 channel_attention.avg_pool 32 16 16 32 1 1 0.0 0.00 0.0 0.0 0.0 0.0 99.99% 0.0
2 channel_attention.fc1 32 8 256.0 0.00 504.0 256.0 1152.0 32.0 0.00% 1184.0
3 channel_attention.fc2 8 32 256.0 0.00 480.0 256.0 1056.0 128.0 0.00% 1184.0
4 channel_attention.relu 8 8 0.0 0.00 8.0 8.0 32.0 32.0 0.00% 64.0
5 channel_attention.sigmoid 32 32 0.0 0.00 0.0 0.0 0.0 0.0 0.00% 0.0
6 spatial_attention.conv 2 16 16 1 16 16 98.0 0.00 49,920.0 25,088.0 2440.0 1024.0 0.00% 3464.0
7 spatial_attention.sigmoid 1 16 16 1 16 16 0.0 0.00 0.0 0.0 0.0 0.0 0.00% 0.0
total 610.0 0.00 50,912.0 25,608.0 0.0 0.0 99.99% 5896.0
==================================================================================================================================================
Total params: 610
--------------------------------------------------------------------------------------------------------------------------------------------------
Total memory: 0.00MB
Total MAdd: 50.91KMAdd
Total Flops: 25.61KFlops
Total MemR+W: 5.76KB
版权归原作者 立Sir 所有, 如有侵权,请联系我们删除。