目录
前言
本文属于 线性回归算法【AIoT阶段三】(尚未更新),这里截取自其中一段内容,方便读者理解和根据需求快速阅读。本文通过公式推导+代码两个方面同时进行,因为涉及到代码的编译运行,如果你没有
N
u
m
P
y
NumPy
NumPy,
P
a
n
d
a
s
Pandas
Pandas,
M
a
t
p
l
o
t
l
i
b
Matplotlib
Matplotlib 的基础,建议先修文章:数据分析三剑客【AIoT阶段一(下)】(十万字博文 保姆级讲解),本文是梯度下降的第二部分,学之前需先修:梯度下降【无约束最优化问题】,后续还会有:**梯度下降优化**,**梯度下降优化进阶****(暂未更新)**
1.梯度下降方法
1.1 三种梯度下降不同
🚩梯度下降分三类:批量梯度下降
B
G
D
BGD
BGD(**Batch Gradient Descent**)、小批量梯度下降
M
B
G
D
MBGD
MBGD(**Mini-Batch Gradient Descent**)、随机梯度下降
S
G
D
SGD
SGD(**Stochastic Gradient Descent**)。
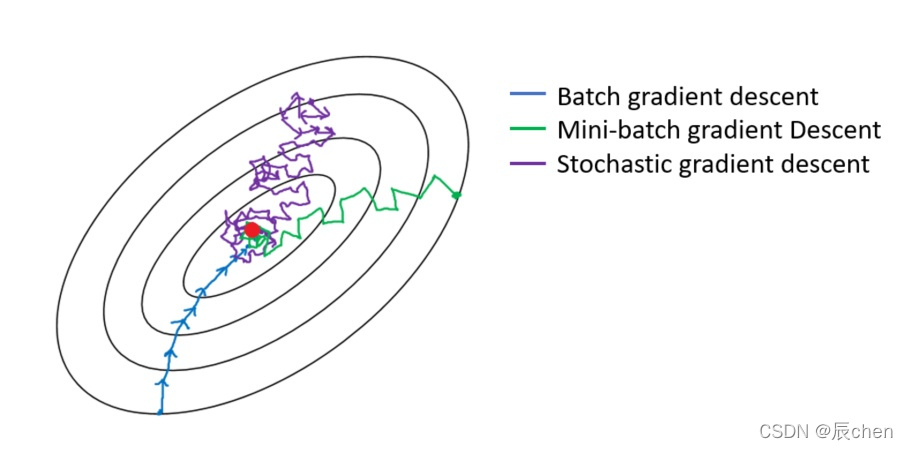
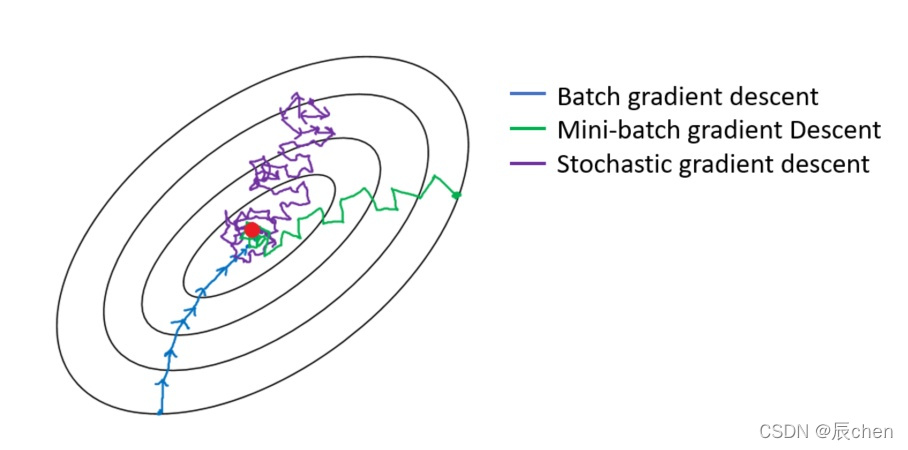
三种梯度下降有什么不同呢?我们从梯度下降步骤开始讲起,梯度下降步骤分以下四步:
- 1、随机赋值, R a n d o m Random Random 随机数生成 θ \theta θ,随机一组数值 w 0 、 w 1 … … w n w_0、w_1……w_n w0、w1……wn
- 2、求梯度 g g g ,梯度代表曲线某点上的切线的斜率,沿着切线往下就相当于沿着坡度最陡峭的方向下降
- 3、 i f if if g < 0 g < 0 g<0, θ \theta θ 变大, i f if if g > 0 g > 0 g>0, θ \theta θ 变小
- 4、判断是否收敛 c o n v e r g e n c e convergence convergence,如果收敛跳出迭代,如果没有达到收敛,回第 2 2 2 步再次执行 2 2 2 ~ 4 4 4 步收敛的判断标准是:随着迭代进行损失函数 L o s s Loss Loss,变化非常微小甚至不再改变,即认为达到收敛
三种梯度下降不同,体现在第二步中:
B G D BGD BGD 是指在**每次迭代**使用**所有样本**来进行梯度的更新M B G D MBGD MBGD 是指在**每次迭代**使用**一部分样本**(所有样本 500 500 500 个,使用其中 32 32 32 个样本)来进行梯度的更新S G D SGD SGD 是指**每次迭代**随机选择**一个样本**来进行梯度更新
1.2 线性回归梯度更新公式
🚩回顾上一讲公式!
最小二乘法公式如下:
J
(
θ
)
=
1
2
∑
i
=
1
n
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
J(\theta) = \frac{1}{2}\sum\limits_{i = 1}^n(h_{\theta}(x^{(i)}) - y^{(i)})^2
J(θ)=21i=1∑n(hθ(x(i))−y(i))2
矩阵写法:
J
(
θ
)
=
1
2
(
X
θ
−
y
)
T
(
X
θ
−
y
)
J(\theta) = \frac{1}{2}(X\theta - y)^T(X\theta - y)
J(θ)=21(Xθ−y)T(Xθ−y)
接着我们来讲解如何求解上面梯度下降的第
2
2
2 步,即我们要推导出损失函数的导函数来。
θ j n + 1 = θ j n − η ∗ ∂ J ( θ ) ∂ θ j \theta_j^{n + 1} = \theta_j^{n} - \eta * \frac{\partial J(\theta)}{\partial \theta_j} θjn+1=θjn−η∗∂θj∂J(θ) 其中 j j j 表示第 j j j 个系数∂ J ( θ ) ∂ θ j = ∂ ∂ θ j 1 2 ( h θ ( x ) − y ) 2 \frac{\partial J(\theta)}{\partial \theta_j} = \frac{\partial}{\partial \theta_j}\frac{1}{2}(h_{\theta}(x) - y)^2 ∂θj∂J(θ)=∂θj∂21(hθ(x)−y)2 = 1 2 ∗ 2 ( h θ ( x ) − y ) ∂ ∂ θ j ( h θ ( x ) − y ) = \frac{1}{2}*2(h_{\theta}(x) - y)\frac{\partial}{\partial \theta_j}(h_{\theta}(x) - y)=21∗2(hθ(x)−y)∂θj∂(hθ(x)−y)
( 1 ) (1)(1)
= ( h θ ( x ) − y ) ∂ ∂ θ j ( ∑ i = 0 n θ i x i − y ) = (h_{\theta}(x) - y)\frac{\partial}{\partial \theta_j}(\sum\limits_{i = 0}^n\theta_ix_i - y)=(hθ(x)−y)∂θj∂(i=0∑nθixi−y)
( 2 ) (2)(2)
= ( h θ ( x ) − y ) x j = (h_{\theta}(x) - y)x_j=(hθ(x)−y)xj
( 3 ) (3)(3)
x 2 x^2x2的导数就是
2 x 2x2x,根据链式求导法则,我们可以推出上面第
( 1 ) (1)(1) 步。然后是多元线性回归,所以
h θ ( x ) h_{\theta}(x)hθ(x) 就 是
θ T x \theta^TxθTx 即是
w 0 x 0 + w 1 x 1 + … … + w n x n w_0x_0 + w_1x_1 + …… + w_nx_nw0x0+w1x1+……+wnxn 即
∑ i = 0 n θ i x i \sum\limits_{i = 0}^n\theta_ix_ii=0∑nθixi。到这里我们是对
θ j \theta_jθj 来求偏导,那么和
w j w_jwj 没有关系的可以忽略不计,所以只剩下
x j x_jxj。
我们可以得到结论就是
θ
j
\theta_j
θj 对应的梯度与预测值
y
^
\hat{y}
y^ 和真实值
y
y
y 有关,这里
y
^
\hat{y}
y^ 和
y
y
y 是列向量(即多个数据),同时还与
θ
j
\theta_j
θj 对应的特征维度
x
j
x_j
xj 有关,这里
x
j
x_j
xj 是原始数据集矩阵的第
j
j
j 列。如果我们分别去对每个维度
θ
0
、
θ
1
…
…
θ
n
\theta_0、\theta_1……\theta_n
θ0、θ1……θn 求偏导,即可得到所有维度对应的梯度值。
g 0 = ( h θ ( x ) − y ) x 0 g_0 = (h_{\theta}(x) - y)x_0 g0=(hθ(x)−y)x0g 1 = ( h θ ( x ) − y ) x 1 g_1 = (h_{\theta}(x) - y)x_1 g1=(hθ(x)−y)x1- ……
g j = ( h θ ( x ) − y ) x j g_j = (h_{\theta}(x) - y)x_j gj=(hθ(x)−y)xj
总结:
θ
j
n
+
1
=
θ
j
n
−
η
∗
(
h
θ
(
x
)
−
y
)
x
j
\theta_j^{n + 1} = \theta_j^{n} - \eta * (h_{\theta}(x) - y )x_j
θjn+1=θjn−η∗(hθ(x)−y)xj
1.3 批量梯度下降
B
G
D
BGD
BGD
🚩批量梯度下降法是最原始的形式,它是指在每次迭代使用所有样本来进行梯度的更新。每次迭代参数更新公式如下:
θ
j
n
+
1
=
θ
j
n
−
η
∗
1
n
∑
i
=
1
n
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\theta_j^{n + 1} = \theta_j^{n} - \eta *\frac{1}{n}\sum\limits_{i = 1}^{n} (h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)}
θjn+1=θjn−η∗n1i=1∑n(hθ(x(i))−y(i))xj(i)
去掉
1
n
\frac{1}{n}
n1 也可以,因为它是一个常量,可以和
η
\eta
η 合并
θ
j
n
+
1
=
θ
j
n
−
η
∗
∑
i
=
1
n
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\theta_j^{n + 1} = \theta_j^{n} - \eta *\sum\limits_{i = 1}^{n} (h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)}
θjn+1=θjn−η∗i=1∑n(hθ(x(i))−y(i))xj(i)
矩阵写法:
θ
n
+
1
=
θ
n
−
η
∗
X
T
(
X
θ
−
y
)
\theta^{n + 1} = \theta^{n} - \eta * X^T(X\theta -y)
θn+1=θn−η∗XT(Xθ−y)
其中
𝑖
=
1
,
2
,
.
.
.
,
n
𝑖 = 1, 2, ..., n
i=1,2,...,n 表示样本数,
𝑗
=
0
,
1
…
…
𝑗 = 0, 1……
j=0,1…… 表示特征数,**这里我们使用了偏置项,即解决
x
0
(
i
)
=
1
x_0^{(i)} = 1
x0(i)=1**。
注意这里更新时存在一个求和函数,即为对所有样本进行计算处理!
优点:
(1)一次迭代是对所有样本进行计算,此时利用矩阵进行操作,实现了并行。
(2)由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。当目标函数为凸函数时,
B
G
D
BGD
BGD 一定能够得到全局最优。
缺点:
(1)当样本数目
n
n
n 很大时,每迭代一步都需要对所有样本计算,训练过程会很慢。
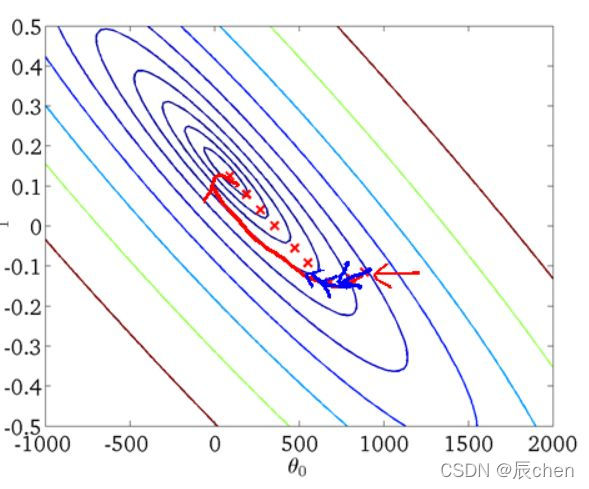
从迭代的次数上来看,
B
G
D
BGD
BGD 迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下:
1.4 随机梯度下降
S
G
D
SGD
SGD
🚩随机梯度下降法不同于批量梯度下降,随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。每次迭代参数更新公式如下:
θ
j
n
+
1
=
θ
j
n
−
η
∗
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\theta_j^{n + 1} = \theta_j^{n} - \eta *(h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)}
θjn+1=θjn−η∗(hθ(x(i))−y(i))xj(i)
批量梯度下降算法每次都会使用全部训练样本,因此这些计算是冗余的,因为每次都使用完全相同的样本集。而随机梯度下降算法每次只随机选择一个样本来更新模型参数,因此每次的学习是非常快速的。
优点:
(1)由于不是在全部训练数据上的更新计算,而是在每轮迭代中,随机选择一条数据进行更新计算,这样每一轮参数的更新速度大大加快。
缺点:
(1)准确度下降。由于即使在目标函数为强凸函数的情况下,
S
G
D
SGD
SGD 仍旧无法做到线性收敛。
(2)可能会收敛到局部最优,由于单个样本并不能代表全体样本的趋势。
解释一下为什么SGD收敛速度比BGD要快:
- 这里我们假设有 30 W 30W 30W 个样本,对于 B G D BGD BGD 而言,每次迭代需要计算 30 W 30W 30W 个样本才能对参数进行一次更新,需要求得最小值可能需要多次迭代(假设这里是 10 10 10)。
- 而对于 S G D SGD SGD,每次更新参数只需要一个样本,因此若使用这30W个样本进行参数更新,则参数会被迭代 30 W 30W 30W 次,而这期间, S G D SGD SGD 就能保证能够收敛到一个合适的最小值上了。
- 也就是说,在收敛时, B G D BGD BGD 计算了 10 × 30 W 10×30W 10×30W 次,而 S G D SGD SGD 只计算了 1 × 30 W 1×30W 1×30W 次。
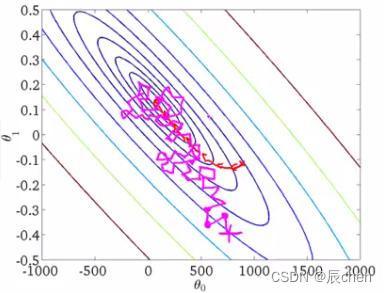
从迭代的次数上来看,
S
G
D
SGD
SGD 迭代的次数较多,在解空间的搜索过程就会盲目一些。其迭代的收敛曲线示意图可以表示如下:
1.5 小批量梯度下降
M
B
G
D
MBGD
MBGD
🚩小批量梯度下降,是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是:每次迭代使用总样本中的一部分
(
b
a
t
c
h
s
i
z
e
)
(batch_size)
(batchsize) 样本来对参数进行更新。这里我们假设
b
a
t
c
h
s
i
z
e
=
20
batch_size = 20
batchsize=20,样本数
n
=
1000
n = 1000
n=1000 。实现了更新速度与更新次数之间的平衡。每次迭代参数更新公式如下:
θ
j
n
+
1
=
θ
j
n
−
η
∗
1
b
a
t
c
h
_
s
i
z
e
∑
i
=
1
b
a
t
c
h
_
s
i
z
e
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\theta_j^{n + 1} = \theta_j^{n} - \eta *\frac{1}{batch\_size}\sum\limits_{i = 1}^{batch\_size} (h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)}
θjn+1=θjn−η∗batch_size1i=1∑batch_size(hθ(x(i))−y(i))xj(i)
相对于随机梯度下降算法,小批量梯度下降算法降低了收敛波动性, 即降低了参数更新的方差,使得更新更加稳定。相对于全量梯度下降,其提高了每次学习的速度。并且其不用担心内存瓶颈从而可以利用矩阵运算进行高效计算。
一般情况下,小批量梯度下降是梯度下降的推荐变体,特别是在深度学习中。每次随机选择
2
2
2 的幂数个样本来进行学习,例如:
8
8
8、
16
16
16、
32
32
32、
64
64
64、
128
128
128、
256
256
256。因为计算机的结构就是二进制的。但是也要根据具体问题而选择,实践中可以进行多次试验, 选择一个更新速度与更次次数都较适合的样本数。
M
B
G
D
MBGD
MBGD 梯度下降迭代的收敛曲线更加温柔一些:
2.代码实现梯度下降
2.1 批量梯度下降
B
G
D
BGD
BGD
2.1.1 一元一次线性回归
import numpy as np
# 创建数据
X = np.random.rand(100,1)
w, b = np.random.randint(1,10, size =2)# 增加噪声,也被称为"加盐"
y = w * X + b + np.random.rand(100,1)# 把b作为偏置项,截距对应系数 x_0 = 1, 更新 X
X = np.concatenate([X, np.full(shape =(100,1),
fill_value =1)], axis =1)# 循环次数
epoches =10000# 学习率
eta =0.01# 要求解的系数,"瞎蒙的"
theta = np.random.randn(2,1)for i inrange(epoches):# 批量梯度下降,X为矩阵,包含所有的数据
g = X.T.dot(X.dot(theta)- y)# 根据公式计算的梯度
theta = theta - eta * g
print('真实的斜率、截距:', w, b)print('使用BGD求的斜率、截距:', theta[0], theta[1])
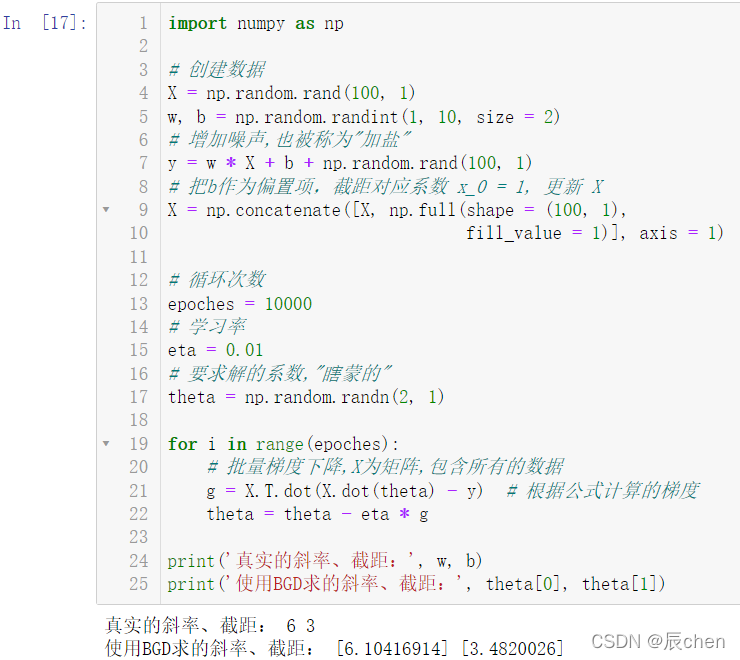
可以看出,我们求出的数据和真实的数据还是有一定的差距的,这就是加了 噪声(加盐) 的作用结果,但这样的计算数据才是更加真实的,因为现实生活中的数据是不可能完美的。
下图是梯度下降的示意图: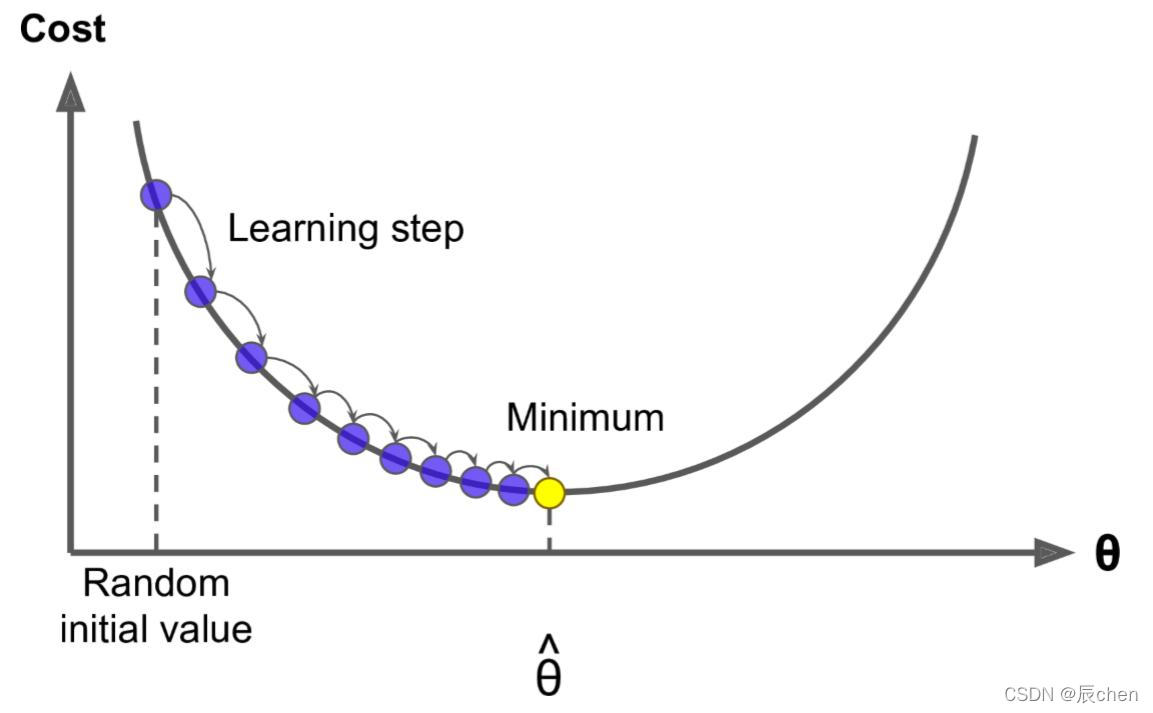
我们可以看出,对于刚开始进行梯度下降的时候,
L
e
a
r
n
i
n
g
Learning
Learning
s
t
e
p
step
step 比较大,即学习率的值比较大,在越接近正确答案的时候,
L
e
a
r
n
i
n
g
Learning
Learning
s
t
e
p
step
step 就变得越小,这其实给了我们一个思路,即我们的
e
t
a
eta
eta 可以跟着梯度下降的循环次数动态的进行变化:
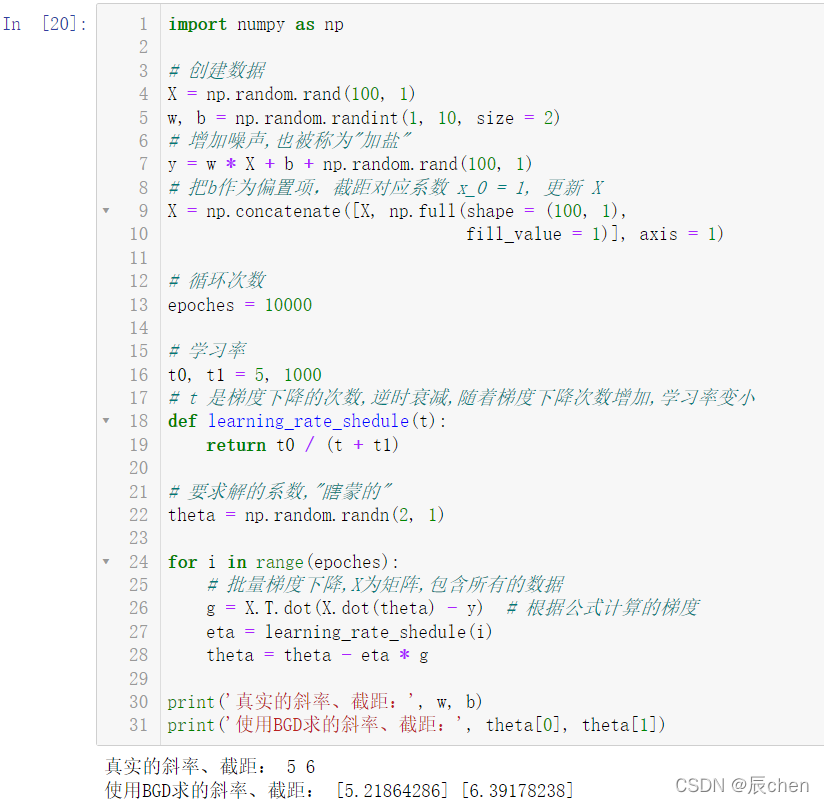
import numpy as np
# 创建数据
X = np.random.rand(100,1)
w, b = np.random.randint(1,10, size =2)# 增加噪声,也被称为"加盐"
y = w * X + b + np.random.rand(100,1)# 把b作为偏置项,截距对应系数 x_0 = 1, 更新 X
X = np.concatenate([X, np.full(shape =(100,1),
fill_value =1)], axis =1)# 循环次数
epoches =10000# 学习率
t0, t1 =5,1000# t 是梯度下降的次数,逆时衰减,随着梯度下降次数增加,学习率变小deflearning_rate_shedule(t):return t0 /(t + t1)# 要求解的系数,"瞎蒙的"
theta = np.random.randn(2,1)for i inrange(epoches):# 批量梯度下降,X为矩阵,包含所有的数据
g = X.T.dot(X.dot(theta)- y)# 根据公式计算的梯度
eta = learning_rate_shedule(i)
theta = theta - eta * g
print('真实的斜率、截距:', w, b)print('使用BGD求的斜率、截距:', theta[0], theta[1])
2.1.2 八元一次线性回归
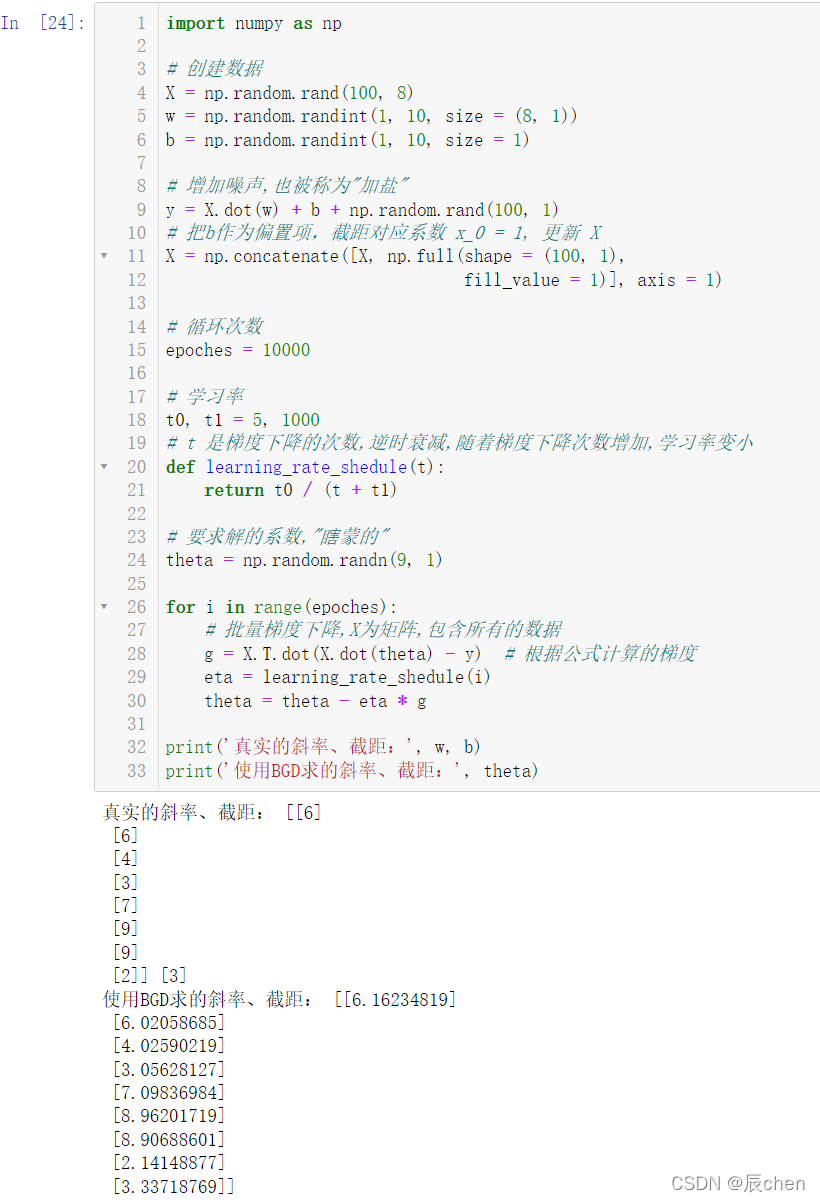
import numpy as np
# 创建数据
X = np.random.rand(100,8)
w = np.random.randint(1,10, size =(8,1))
b = np.random.randint(1,10, size =1)# 增加噪声,也被称为"加盐"
y = X.dot(w)+ b + np.random.rand(100,1)# 把b作为偏置项,截距对应系数 x_0 = 1, 更新 X
X = np.concatenate([X, np.full(shape =(100,1),
fill_value =1)], axis =1)# 循环次数
epoches =10000# 学习率
t0, t1 =5,1000# t 是梯度下降的次数,逆时衰减,随着梯度下降次数增加,学习率变小deflearning_rate_shedule(t):return t0 /(t + t1)# 要求解的系数,"瞎蒙的"
theta = np.random.randn(9,1)for i inrange(epoches):# 批量梯度下降,X为矩阵,包含所有的数据
g = X.T.dot(X.dot(theta)- y)# 根据公式计算的梯度
eta = learning_rate_shedule(i)
theta = theta - eta * g
print('真实的斜率、截距:', w, b)print('使用BGD求的斜率、截距:', theta)
2.2 随机梯度下降
S
G
D
SGD
SGD
2.2.1 一元一次线性回归
import numpy as np
# 创建数据
X = np.random.rand(100,1)
w, b = np.random.randint(1,10, size =2)# 增加噪声,也被称为"加盐"
y = w * X + b + np.random.rand(100,1)# 把b作为偏置项,截距对应系数 x_0 = 1, 更新 X
X = np.concatenate([X, np.full_like(X, fill_value =1)], axis =1)# 循环次数
epoches =100# 学习率
t0, t1 =5,1000# t 是梯度下降的次数,逆时衰减,随着梯度下降次数增加,学习率变小deflearning_rate_shedule(t):return t0 /(t + t1)
theta = np.random.randn(2,1)
cnt =0# 表示训练的次数for t inrange(epoches):
index = np.arange(100)
np.random.shuffle(index)# 洗牌,打乱顺序# NumPy 花式索引
X = X[index]
y = y[index]for i inrange(100):
X_i = X[[i]]
y_i = y[[i]]# 根据这一个样本,进行计算梯度
g = X_i.T.dot(X_i.dot(theta)- y_i)
eta = learning_rate_shedule(cnt)
cnt +=1
theta -= eta * g
print('真实的斜率、截距:', w, b)print('使用SGD求的斜率、截距:', theta[0], theta[1])

2.2.2 五元一次线性回归
import numpy as np
# 创建数据
X = np.random.rand(100,5)
w = np.random.randint(1,10, size =(5,1))
b = np.random.randint(1,10, size =1)# 增加噪声,也被称为"加盐"
y = X.dot(w)+ b + np.random.rand(100,1)# 把b作为偏置项,截距对应系数 x_0 = 1, 更新 X
X = np.concatenate([X, np.full(shape =(100,1), fill_value =1)], axis =1)# 循环次数
epoches =100# 学习率
t0, t1 =5,1000# t 是梯度下降的次数,逆时衰减,随着梯度下降次数增加,学习率变小deflearning_rate_shedule(t):return t0 /(t + t1)
theta = np.random.randn(6,1)
cnt =0# 表示训练的次数for t inrange(epoches):
index = np.arange(100)
np.random.shuffle(index)# 洗牌,打乱顺序# NumPy 花式索引
X = X[index]
y = y[index]for i inrange(100):
X_i = X[[i]]# 两个[]:可以进行矩阵运算
y_i = y[[i]]# 根据这一个样本,进行计算梯度
g = X_i.T.dot(X_i.dot(theta)- y_i)
eta = learning_rate_shedule(cnt)
cnt +=1
theta -= eta * g
print('真实的斜率、截距:', w, b)print('使用SGD求的斜率、截距:', theta)

2.3 小批量梯度下降
M
B
G
D
MBGD
MBGD
2.3.1 一元一次线性回归
import numpy as np
# 1、创建数据集X,y
X = np.random.rand(100,1)
w,b = np.random.randint(1,10,size =2)
y = w * X + b + np.random.randn(100,1)# 2、使用偏置项x_0 = 1,更新X
X = np.c_[X, np.ones((100,1))]# 3、定义一个函数来调整学习率
t0, t1 =5,500deflearning_rate_schedule(t):return t0/(t + t1)# 4、创建超参数轮次、样本数量、小批量数量
epochs =100
n =100
batch_size =16
num_batches =int(n / batch_size)# 5、初始化 W0...Wn,标准正太分布创建W
θ = np.random.randn(2,1)# 6、多次for循环实现梯度下降,最终结果收敛for epoch inrange(epochs):# 在双层for循环之间,每个轮次开始分批次迭代之前打乱数据索引顺序
index = np.arange(n)
np.random.shuffle(index)
X = X[index]
y = y[index]for i inrange(num_batches):# 一次取一批数据16个样本
X_batch = X[i * batch_size :(i +1)* batch_size]
y_batch = y[i * batch_size :(i +1)* batch_size]
g = X_batch.T.dot(X_batch.dot(θ)- y_batch)
learning_rate = learning_rate_schedule(epoch * n + i)
θ = θ - learning_rate * g
print('真实斜率和截距是:', w, b)print('梯度下降计算斜率和截距是:',θ)

2.3.2 三元一次线性回归
import numpy as np
# 1、创建数据集X,y
X = np.random.rand(100,3)
w = np.random.randint(1,10,size =(3,1))
b = np.random.randint(1,10,size =1)
y = X.dot(w)+ b + np.random.randn(100,1)# 2、使用偏置项 X_0 = 1,更新X
X = np.c_[X, np.ones((100,1))]# 3、定义一个函数来调整学习率
t0, t1 =5,500deflearning_rate_schedule(t):return t0/(t + t1)# 4、创建超参数轮次、样本数量、小批量数量
epochs =10000
n =100
batch_size =16
num_batches =int(n / batch_size)# 5、初始化 W0...Wn,标准正太分布创建W
θ = np.random.randn(4,1)# 6、多次for循环实现梯度下降,最终结果收敛for epoch inrange(epochs):# 在双层for循环之间,每个轮次开始分批次迭代之前打乱数据索引顺序
index = np.arange(n)
np.random.shuffle(index)
X = X[index]
y = y[index]for i inrange(num_batches):# 一次取一批数据16个样本
X_batch = X[i * batch_size :(i +1)* batch_size]
y_batch = y[i * batch_size :(i +1)* batch_size]
g = X_batch.T.dot(X_batch.dot(θ)- y_batch)
learning_rate = learning_rate_schedule(epoch * n + i)
θ = θ - learning_rate * g
print('真实斜率和截距是:', w, b)print('梯度下降计算斜率和截距是:',θ)

版权归原作者 辰chen 所有, 如有侵权,请联系我们删除。