《数据结构》队列及其经典面试题

前言

上一篇讲了栈和栈的经典面试题，链接如下：

栈与栈的经典面试题

其实栈和队列是一码事，都是对只能再线性表的一端进行插入和删除。

因此，其实栈和队列可以互相转换！

一、队列的特点

先进先出的数据结构，元素从“队尾”添加到队列中，元素从“队首”出队列 （FIFO）

二、队列的实现

1.基于链表实现队列

现实生活中，有各式各样的“排队”操作。

同样的，队列也有基于数组实现的队列和基于链表实现的队列。

由于出队操作只能在队列的头部进行，若采用数组的方案，每次出队一个元素就得搬移剩下的所有元素向前移动一个单位。

此时采用链表的方案更加适合队列的结构。

2.核心操作

• E poll() : 出队
• offer(E e) : 入队

三、双端队列

双端队列（deque）是指允许两端都可以进行入队和出队操作的队列，deque 是 “double ended queue” 的简称。

那就说明元素可以从队头出队和入队，也可以从队尾出队和入队。

Deque -> Queue的子接口：

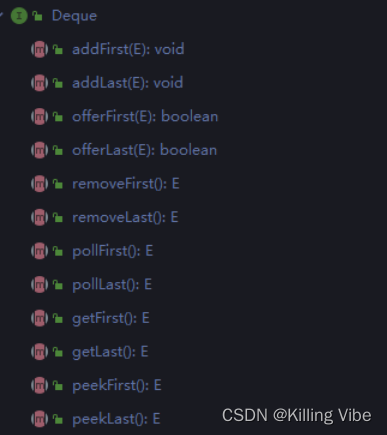
小技巧：

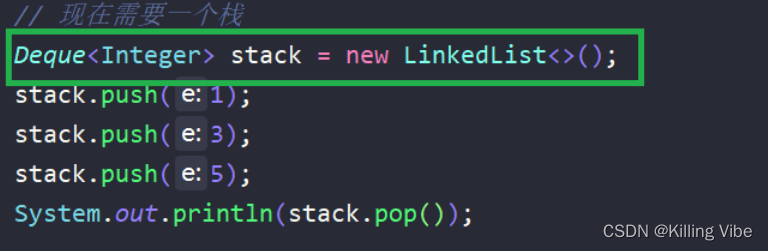
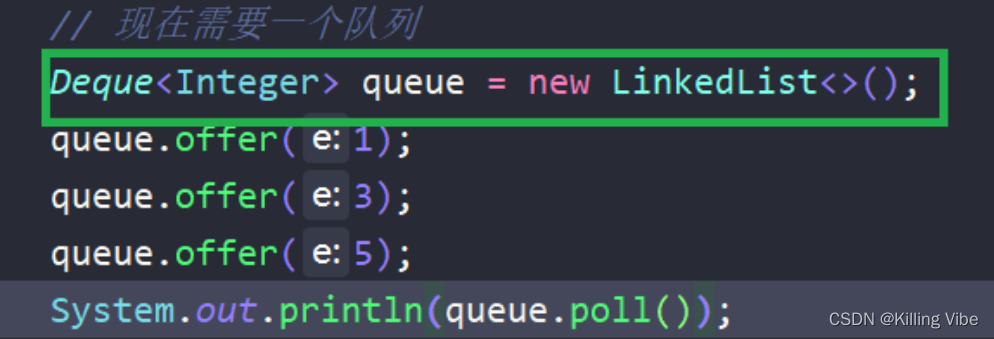
• 大家以后无论使用的是栈还是队列，统一使用双端队列接口！
• 不推荐使用Stack这个类，这个类已经是时代的弃子，效率很低，都是同步操作。
• 双端队列的一个常用子类就是LinkedList。

四、循环队列

1.应用场景

• 操作系统的生产消费者模型
• MySQL数据库的InnoDB存储引擎中的redo日志。

2.实现

1. 基本都是使用长度固定的数组实现，数组在实现队列时，若从数组头部删除元素需要频繁的移动后面的元素，带来的效率比较低。
2. 出队和入队操作，使用两个引用，一个head，一个tail，添加元素在数组尾部添加，删除元素只需要移动head引用指向的地址即可（逻辑删除）。

循环队列就是使用长度固定的数组来实现，数组头部就是队首（head），数组的尾部就时队尾（tail）。数组[head…tail]是循环队列的有效元素。

例如：

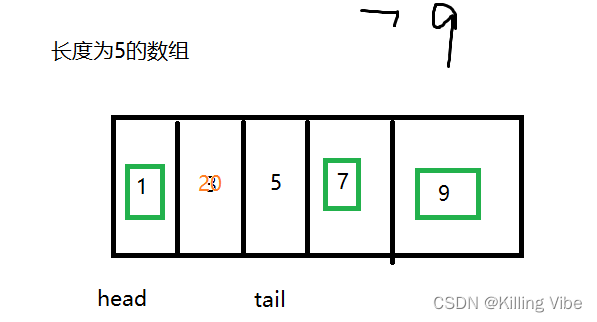
• head永远指向循环队列的第一个元素
• tail永远指向循环队列有效元素的后一个位置

循环队列在删除元素时，不需要进行数据的搬移，当有新的元素在添加时就会覆盖掉之前的元素。

所谓的循环队列指的是当head或者tail引用走到数组末尾时，下一次再继续向后移动，其实是返回数组的头部继续操作。

3.判空和判满

由于tail指向的是有效数组后一个位置，所以当tail走到如图所示的head == tail 情况时：

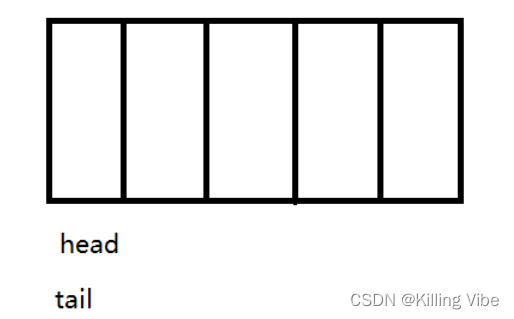
此时我们没法区分当前循环队列到底是空还是满！！！

所以在循环队列中，需要浪费一个空间来判断队列是否已满，如下图所示：

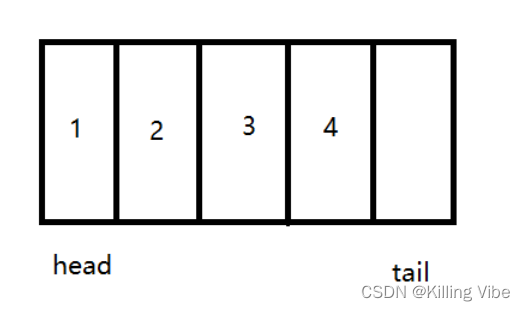
结论：

1. 此时当 (tail+1)%n == head 时，认为此时循环队列已满。
2. head和tail的移动不能简单的+1，而要使用取模操作，取数组长度。
3. 当head == tail 时 ，认为此时循环队列为空。

4.最后一个元素的索引

• 除了tail这个引用指向0这个位置以外，其他情况的最后一个索引 = tail - 1
• 当 tail = 0 时，最后一个元素就在数组的末尾，索引 = data.length - 1

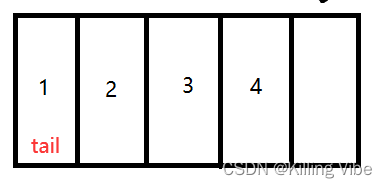
代码如下：

int lastIndex = tail ==0? data.length -1: tail -1

五、队列的常见问题

1.用队列实现栈

链接如下：225.用队列实现栈

解题思路：

思路1：（双队列思路）

这个问题的本质和双栈实现最小栈是相同的思路，一定要保证其中一个队列就是进行实际元素存储的，另一个队列就是作为辅助操作。

q1永远是存储元素的队列，新元素添加到q2中，将此时q1中的所有元素出队再入队q2恰好就能实现添加顺序和出队顺序相反的操作。

1. 新元素永远入q2
2. 将老元素q1依次出队再入q2 （这样就交换了元素的先后顺序）
3. q1和q2交换引用

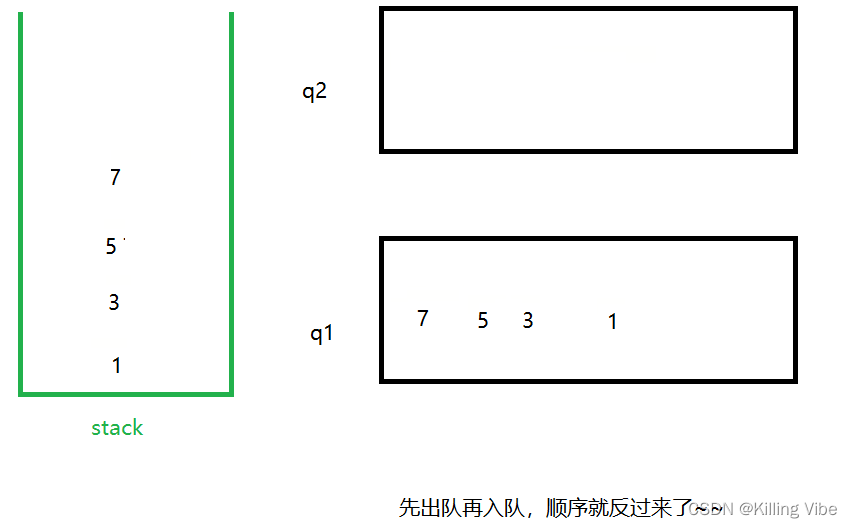
• 其中一个队列q1永远都是存储元素的队列，栈的pop就是s1的poll，栈的peek就是s1的peek，栈的push就是s1的offer。 （**所以整个题的核心操作就是push()**）
• 以保证s1和栈的操作一一对应。
• 另外一个队列就是作为辅助操作。

代码如下：

classMyStack{Deque<Integer> temp;Deque<Integer> q1;Deque<Integer> q2;publicMyStack(){
        q1 =newLinkedList<>();
        q2 =newLinkedList<>();}publicvoidpush(int x){
        q2.offer(x);while(!q1.isEmpty()){
            q2.offer(q1.poll());}
        temp = q1;
        q1 = q2 ;
        q2 = temp;}publicintpop(){return q1.poll();}publicinttop(){return q1.peek();}publicbooleanempty(){return q1.isEmpty();}}

思路2：（单队列思路）

1. 先记录下当前队列中的元素个数n
2. 将新元素直接入队
3. 为了让新元素变成队首元素，连续出队n次（新元素的之前的所有元素都出队列，此时新元素变成了队首元素），再依次入队n次即可。

代码如下：

classMyStack{privateDeque<Integer> queque;privateint length=0;//1.先记录一下栈此时的元素个数publicMyStack(){
        queque=newLinkedList<>();}publicvoidpush(int x){
        queque.offer(x);//2.新元素直接入队//3.把新元素之前的元素挨个出队再入队，此时最新的元素就是队头元素for(int i=0;i<length;i++){
            queque.offer(queque.poll());}
        length++;}publicintpop(){
        length--;return queque.poll();}publicinttop(){return queque.peek();}publicbooleanempty(){return queque.isEmpty();}}

2.用栈实现队列

链接如下：用栈实现队列

解题思路：

思路1：(入队 - 时间复杂度为O(n)，出队 - O(1))

定义s1永远是保存元素的栈

1. 先将s1中的现有元素依次弹出放入s2
2. 将新元素入s1 => 此时这个新元素就变成了s1的栈底（队尾元素）
3. 将s2中的元素再依次弹回来（先进先出）

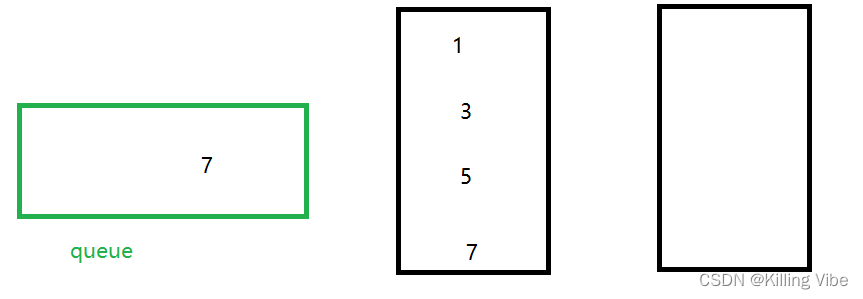
代码如下：

classMyQueue{Deque<Integer> s1;Deque<Integer> s2;publicMyQueue(){
        s1 =newLinkedList<>();
        s2 =newLinkedList<>();}publicvoidpush(int x){while(!s1.isEmpty()){
            s2.push(s1.pop());}
        s1.push(x);while(!s2.isEmpty()){
            s1.push(s2.pop());}}publicintpop(){return s1.pop();}publicintpeek(){return s1.peek();}publicbooleanempty(){return s1.isEmpty();}}

思路2：(入队 - 时间复杂度为O(1)，出队-摊还复杂度O(1))

1. push是正常push的，核心操作在pop里面
2. push进s1的元素依次出栈再入s2栈的时候，出入顺序就会颠倒
3. 根据上述特性，把s2的栈顶当作队首就行了，因为队列都是队首出队的。
4. 每次pop先判断当前s2是否为空，若为空，则把s1中的元素全部出栈并且压进s2里面，此时s2的栈顶就是队首元素（先进先出）。若不为空，证明上一轮push进来的元素还没pop完，继续pop当前s2的栈顶就行。

classMyQueue{Deque<Integer> s1 ;Deque<Integer> s2 ;publicMyQueue(){
        s1 =newLinkedList<>();
        s2 =newLinkedList<>();}publicvoidpush(int x){
        s1.push(x);}publicintpop(){if(s2.isEmpty()){while(!s1.isEmpty()){
                s2.push(s1.pop());}}return s2.pop();}publicintpeek(){if(s2.isEmpty()){while(!s1.isEmpty()){
                s2.push(s1.pop());}}return s2.peek();}publicbooleanempty(){return s1.isEmpty()&& s2.isEmpty();}}

总结

以上就是队列及其经典面试题的全部内容了，有帮助的话麻烦各位给个三连~~感谢！！！