前端必会算法基础

数据结构和算法基础

作为一名合格的前端，学习算法是必不可少的，而且好点的公司对算法题目也是很重视的。本文章对数据结构和算法做了很详细的介绍，感兴趣的朋友可以收藏起来慢慢看（算法入门基础）

排序算法

算法最重要的是严谨性，不能出错，注意判空等情况

排序不是比较大小，排序是比较和交换

普通排序

let arr =[3,2,5,9,4,8,1,6,7];functiongetMin(arr){//每次返回一个最小值并将这个最小值删除if(arr ==null|| arr.length ==0)return[];let index =-1;for(let i =0; i < arr.length; i++){if(arr[i]!=null&& arr[index]> arr[i]|| arr[i]!=null&& index ==-1){
            index = i;}}let result = arr[index];
    arr[index]=null;return result;}functionsort(arr){//每次将最小值按顺序存到newArr中if(arr ==null|| arr.length ==0)return[];let newArr =newArray(arr.length);for(let j =0; j < newArr.length; j++){
        newArr[j]=getMin(arr);}return newArr;}

console.log(sort(arr));

冒泡排序和选择排序

let arr =[3,2,5,9,4,8,1,6,7];// 排序不是比较大小，排序是比较和交换functioncompare(a, b){//比较a和b,比较什么由你决定if(a > b)returntrue;elsereturnfalse;}functionexchange(arr, a, b){//交换就是调换数组中a和b位置的值[arr[a], arr[b]]=[arr[b], arr[a]]}/**
 * 冒泡排序：两两比较,不符合条件则交换两者位置
 * @param {*} arr 
 */functionsort(arr){//算法可以是冒泡排序，也可以是选择排序等等if(arr ==null|| arr.length ==0)return[];for(let i =0; i < arr.length -1; i++){for(let j =0; j < arr.length -1- i; j++){if(compare(arr[j], arr[j +1])==true){exchange(arr, j, j +1);}}}
    console.log(arr);}// sort(arr);/**
 * 选择排序：每次循环找到最大的值和末尾的值交换
 * @param {*} arr 
 */functionsort1(arr){if(arr ==null|| arr.length ==0)return;for(let i =0; i < arr.length; i++){let maxIndex =0;for(let j =0; j < arr.length - i; j++){if(compare(arr[maxIndex], arr[j])!=true){
                maxIndex = j;}}exchange(arr, maxIndex, arr.length -1- i);}
    console.log(arr);}sort1(arr)

快速排序

简单快速排序

let arr =[3,2,5,9,4,8,1,6,7];/**
 * 简单快速排序：每次取数组第一位与其他比较，符合条件放右边，不符合放左边
 * @param {*} arr 
 * @returns 
 */functionquickSort(arr){if(arr ==null|| arr.length ==0)return[];//严谨性判断let leader = arr[0];let left =[];let right =[];for(let i =1; i < arr.length; i++){if(arr[i]> leader){
            right.push(arr[i])}else{
            left.push(arr[i])}}
    left =quickSort(left);
    right =quickSort(right);// left.push(leader);// return left.concat(right);return[...left, leader,...right];}
console.log(quickSort(arr));

标准快速排序

let arr =[3,2,5,9,4,8,1,6,7];functionswap(arr, a, b){[arr[a], arr[b]]=[arr[b], arr[a]]}/**
 * 标准快速排序：通过两个指针依次往中间移动，和相对点比较，也就是和数组第一个元素比较
 * @param {*} arr 
 * @returns 
 */functionquickSort(arr, begin, end){if(arr ==null|| arr.length ==0|| begin >= end -1)return[];//严谨性判断let left = begin,
        right = end;do{//do...while循环至少执行一次// 左右两个指针依次往中间移动和标志点比较，符合条件继续do left++;while(left < right && arr[left]< arr[begin]);do right--;while(right > left && arr[right]> arr[begin]);if(left < right){//两边都不符合条件则互换他们的值让其符合条件swap(arr, left, right);}}while(left < right);// 需要将标志点和中间位置进行交换let flag = left == right ? right -1: right;swap(arr, begin, flag);// 进行递归，完成后续排序quickSort(arr, begin, flag);quickSort(arr, flag +1, end);}functionquickSort1(arr){quickSort(arr,0, arr.length);}quickSort1(arr);
console.log(arr);

一维数据结构

一维数据结构也叫做线性数据结构，强调存储和顺序。

数组

1. 物理存储空间必须是连续的，所以当系统的空间碎片比较多，数组又比较大时，会出现存储不下的情况，尽管系统的剩余空间大于数组的大小。这时操作系统会整理空间的内存，空出一块连续的空间，消耗性能。
2. 底层的数组长度是不可变的，我们之所以可以增加数组的内容是因为js引擎对数组进行了优化，会对数组进行扩容，这会消耗性能- 增加内容：操作系统负责分配你需要的内存空间而不是修改原来的内存空间，所以当内容增加到比原来数组大的时候，会开辟一块新的空间，预定比增加后的数组大的空间，然后将原先的元素复制过来，再加上需要增加的元素，这就叫扩容。- 删除内容：删除中间的一个元素，需要将后面的元素一个个移动到前一个位置，保证数组连续。var arr =[1,2,3,4,5,6];//数组定长时的写法var arr1 =newArray(10)//预定数组长度，尽量保证数组不再扩容，防止消耗性能
3. 数组的变量指向的是数组的第一个元素，而arr[1]中的方括号表示偏移量，操作系统中通过偏移量查询数据的性能是最好的，所以数组指定查询一个元素的位置时，性能是最好的。

链表

需要传递一个链表时，必须传递链表的根节点。每一个节点都认为自己的根节点，每一个节点只有自己的值和下一个节点的引用，没有上一个节点的任何信息，所以每个节点都是起始节点。

1. 链表在空间上不是连续的，所以只要内存够大，就可以存储，不用担心内存碎片，相对的查询速度就比较慢。
2. 链表中的每一个值，都需要开辟一个引用空间，指向链表的下一个节点，浪费了一些空间，但是这些引用是固定的大小，当值比较大时，影响就可以忽略不计了。
3. 链表的增加和删除非常方便 - 增加：在a和b节点中增加c，将a的引用指向c，将c的引用指向b即可。- 删除：只需要将a的引用重新指向b即可，不用在乎c的引用还指向b，以为传递链表时随便哪个节点都不会指向c。

//单链表functionNode(value){this.value = value;this.next =null;}var a =Node(1);var b =Node(2);var c =Node(3);var d =Node(4);
a.next = b;
b.next = c;
c.next = d;
console.log(a.value, a.next.value, a.next.next.value, a.next.next.next.value);//1,2,3,4// 双向链表functionNode(value){this.value = value;this.next =null;this.prev =null;}let link1 =newNode(1);let link2 =newNode(2);let link3 =newNode(3);let link4 =newNode(4);let link5 =newNode(5);

link1.next = link2;
link2.prev = link1;
link2.next = link3;
link3.prev = link2;
link3.next = link4;
link4.prev = link3;
link4.next = link5;
link5.prev = link4;

栈和队列

functionStack(){//栈 先进后出    类似于盒子this.arr =[];this.push=function(value){returnthis.arr.push(value);}this.pop=function(){returnthis.arr.pop();}}var stack =newStack();
stack.push(1)
stack.push(2)
stack.push(3)
console.log(stack.arr);
stack.pop()
console.log(stack.arr);functionQueue(){//队列 先进先出   类似于管道this.arr =[];this.push=function(value){returnthis.arr.push(value);}this.shift=function(){returnthis.arr.shift();}}var queue =newQueue();
queue.push(1)
queue.push(2)
queue.push(3)
console.log(queue.arr);
queue.shift()
console.log(queue.arr);

线性结构的遍历和递归遍历

遍历是指对集合中的每个元素进行获取和查看
递归就是自己调用自己，递归一定要先找一个出口，不然程序会出现死循环

//数组的遍历let arr =[1,2,3,4,5,6]functioneachArr(arr){if(arr ==null){return;}for(let i =0; i < arr.length; i++){
        console.log(arr[i]);}}// eachArr(arr);//数组的递归遍历functioneachArr1(arr, i){if(arr ==null|| i >= arr.length){return;}else{
        console.log(arr[i]);eachArr1(arr, i +1)}}eachArr1(arr,0);//链表的遍历functionNode(value){this.value = value;this.next =null;}let link1 =newNode(1);let link2 =newNode(2);let link3 =newNode(3);let link4 =newNode(4);let link5 =newNode(5);
link1.next = link2;
link2.next = link3;
link3.next = link4;
link4.next = link5;functioneachLink(node){let temp = node;while(true){if(temp !==null){
            console.log(temp.value);}else{break;}
        temp = temp.next;}}// eachLink(link1);//链表的递归遍历functioneachLink1(node){if(node ==null){return;}else{
        console.log(node.value);eachLink1(node.next);}}eachLink1(link1)

链表的逆置

functionNode(value){this.value = value;this.next =null;}let link1 =newNode(1);let link2 =newNode(2);let link3 =newNode(3);let link4 =newNode(4);let link5 =newNode(5);
link1.next = link2;
link2.next = link3;
link3.next = link4;
link4.next = link5;functionnizhi(node){// 先找到最后一个节点，由于链表节点是无法找到上一个节点的，所以这里先找到倒数第二个节点if(node.next.next ==null){//如果node是倒数第二个节点
        node.next.next = node;//最后一个节点的next等于倒数第二个节点return node.next;//返回最后一个节点}else{let result =nizhi(node.next)//将最后一个节点作为根节点参数
        node.next.next = node;//下一个节点的next等于这个节点
        node.next =null;//这个节点的next等于null,防止节点2指向节点1,节点1又指向节点2无限循环return result;//返回最后一个节点,也就是逆置后的第一个节点}}functioneachLink(node){if(node ==null){return;}
    console.log(node.value);eachLink(node.next);}eachLink(nizhi(link1));

二维数据结构

二维数组和拓扑结构（图）

// 二维数组var arr =newArray(4);for(let i =0; i < arr.length; i++){
    arr[i]=newArray(5);}// 拓扑结构(图)functionNode(value){this.value = value;this.neighbor =[];}varA=newNode('a');varB=newNode('b');varC=newNode('c');varD=newNode('d');varE=newNode('e');A.neighbor.push(B)A.neighbor.push(D)A.neighbor.push(E)B.neighbor.push(C)B.neighbor.push(E)D.neighbor.push(E)

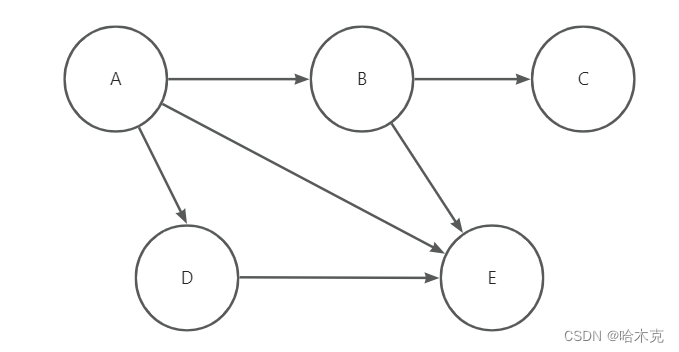
树形结构–有向无环图

• 树形结构有一个根节点，树形结构没有回路
• 根节点：A
• 子节点，父节点
• 叶子节点：B, C, E，F
• 节点：D，既不是根节点，也不是叶子节点的普通节点
• 树的度：3，这颗树分叉最多的的数量
• 树的深度：3，这棵树最深的层数

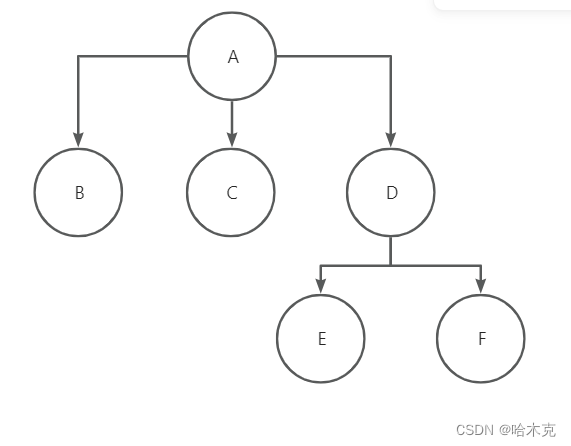
二叉树

• 树的度最多为2的树形结构
• 二叉树中，所有的节点都认为自己的根节点
• 子树：二叉树中，每一个节点或者叶子节点都是一个子树的根节点
• 左子树，右子树

满二叉树

• 所有的叶子节点都在最底层
• 每个非叶子节点都有两个子节点

完全二叉树

国内定义

• 所有的叶子节点都在最底层或者倒数第二层
• 叶子节点都向左靠拢

国际定义

• 所有的叶子节点都在最底层或者倒数第二层
• 节点要是有叶子节点，就必须有两个叶子节点

二叉树的遍历

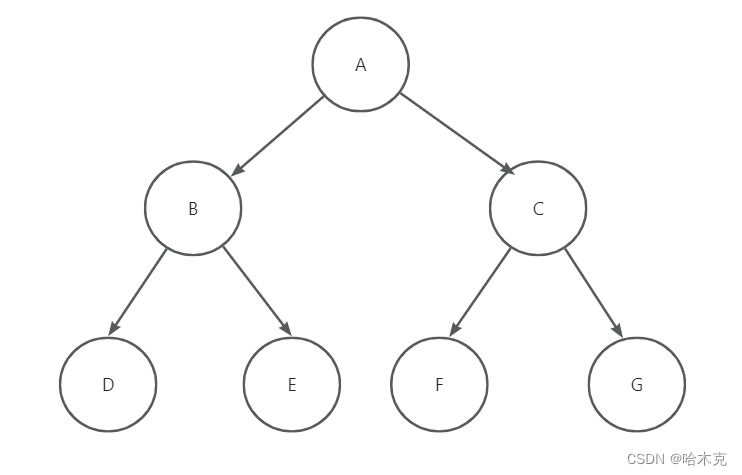
• 前序遍历（先根次序遍历） 先打印当前节点，再打印左边，最后打印右边 ABDECFG
• 中序遍历（中根次序遍历） 先打印左边，再打印当前节点，最后打印右边 DBEAFCG
• 后序遍历（后根次序遍历） 先打印左边，再打印右边，最后打印当前节点 DEBFGCA

// 二叉树的遍历functionNode(value){this.value = value;this.left =null;this.right =null;}let a =newNode('a');let b =newNode('b');let c =newNode('c');let d =newNode('d');let e =newNode('e');let f =newNode('f');let g =newNode('g');

a.left = b;
a.right = c;
b.left = d;
b.right = e;
c.left = f;
c.right = g;functionforTree(node){if(node ==null)return;
    console.log(node.value);//根据打印顺序决定前序，中序，后序forTree(node.left);forTree(node.right)}forTree(a);

还原二叉树

根据二叉树的前序（后序）遍历和中序遍历还原二叉树

functionNode(value){this.value = value;this.left =null;this.right =null;}let qian =['A','B','D','E','C','F','G'];let zhong =['D','B','E','A','F','C','G'];let hou =['D','E','B','F','G','C','A'];functionrestoreTree1(qian, zhong){if(qian ==null|| zhong ==null|| qian.length ==0|| zhong.length ==0|| qian.length != zhong.length)returnnull;let root =newNode(qian[0]);//拿到根节点let index = zhong.indexOf(root.value);//拿到中序遍历中根节点的位置索引找出左右子树let leftQian = qian.slice(1, index +1);let rightQian = qian.slice(index +1, qian.length);let leftZhong = zhong.slice(0, index);let rightZhong = zhong.slice(index +1, zhong.length);// 设置root的左右子树，最后返回root
    root.left =restoreTree1(leftQian, leftZhong);
    root.right =restoreTree1(rightQian, rightZhong);return root;}functionrestoreTree2(hou, zhong){if(hou ==null|| zhong ==null|| hou.length ==0|| zhong.length ==0|| hou.length != zhong.length)returnnull;let root =newNode(hou[hou.length -1]);//拿到根节点let index = zhong.indexOf(root.value);//拿到中序遍历中根节点的位置索引找出左右子树let leftHou = hou.slice(0, index);let rightHou = hou.slice(index, hou.length -1);let leftZhong = zhong.slice(0, index);let rightZhong = zhong.slice(index +1, zhong.length);// 设置root的左右子树，最后返回root
    root.left =restoreTree2(leftHou, leftZhong);
    root.right =restoreTree2(rightHou, rightZhong);return root;}// var root = restoreTree1(qian, zhong);var root =restoreTree2(hou, zhong);
console.log(root.left, root.right);

二叉树的搜索

functionNode(value){this.value = value;this.left =null;this.right =null;}let a =newNode('a');let b =newNode('b');let c =newNode('c');let d =newNode('d');let e =newNode('e');let f =newNode('f');let g =newNode('g');

a.left = b;
a.right = c;
b.left = d;
b.right = e;
c.left = f;
c.right = g;/**
 * 广度优先搜索:每次搜索同一层的节点
 * @param {*} rootList 每一层的节点列表
 * @param {*} target 目标
 */functionextendSearch(rootList, target){if(rootList ==null|| rootList.length ==0|| target ==null)returnfalse;let childList =[];//存储所有节点的子节点for(let i =0; i < rootList.length; i++){if(rootList[i]!=null&& rootList[i].value == target)returntrue;else{if(rootList[i].left){
                childList.push(rootList[i].left);}if(rootList[i].right){
                childList.push(rootList[i].right);}}}returnextendSearch(childList, target);}// console.log(extendSearch([a], 'f'));/**
 * 深度优先搜索和前序遍历的顺序相同:根节点>左子树>右子树
 * @param {*} root 节点
 * @param {*} target 目标
 */functiondeepSearch(root, target){if(root ==null|| target ==null)returnfalse;if(root.value == target)returntrue;let left =deepSearch(root.left, target);let right =deepSearch(root.right, target);return left || right;}// console.log(deepSearch(a,'f'));

二叉树的比较

functionNode(value){this.value = value;this.left =null;this.right =null;}let a1 =newNode('a');let b1 =newNode('b');let c1 =newNode('c');let d1 =newNode('d');let e1 =newNode('e');let f1 =newNode('f');let g1 =newNode('g');

a1.left = b1;
a1.right = c1;
b1.left = d1;
b1.right = e1;
c1.left = f1;
c1.right = g1;let a2 =newNode('a');let b2 =newNode('b');let c2 =newNode('c');let d2 =newNode('d');let e2 =newNode('e');let f2 =newNode('f');let g2 =newNode('g');

a2.left = b2;
a2.right = c2;
b2.left = d2;
b2.right = e2;
c2.left = f2;
c2.right = g2;/**
 * 比较两个二叉树是否相同
 * @param {*} root1 
 * @param {*} root2 
 */functioncompare(root1, root2){if(root1 == root2)returntrue;//是同一棵树if(root1 ==null&& root2 !=null|| root1 !=null& root2 ==null)returnfalse;//一棵树为空let root1Left = root1.left,
        root1Right = root1.right;let root2Left = root2.left,
        root2Right = root2.right;// 左子树和左子树相比，右子树和右子树相比// 二叉树左右子树互换时，左子树和右子树相比，右子树和左子树相比// 其中一个情况符合则两棵树相同returncompare(root1Left, root2Left)&&compare(root1Right, root2Right)||compare(root1Left, root2Right)&&compare(root1Right, root2Left);}

console.log(compare(a1, a2));

二叉树的diff算法

functionNode(value){this.value = value;this.left =null;this.right =null;}let a1 =newNode('a');let b1 =newNode('b');let c1 =newNode('c');let d1 =newNode('d');let e1 =newNode('e');let f1 =newNode('f');let g1 =newNode('g');

a1.left = b1;
a1.right = c1;
b1.left = d1;
b1.right = e1;// c1.left = f1;
c1.right = g1;let a2 =newNode('a');let b2 =newNode('b');let c2 =newNode('z');let d2 =newNode('d');let e2 =newNode('e');let f2 =newNode('f');let g2 =newNode('g');

a2.left = b2;
a2.right = c2;
b2.left = d2;
b2.right = e2;
c2.left = f2;// c2.right = g2;/**
 * 二叉树的diff算法,返回diffList
 * @param {*} root1 
 * @param {*} root2 
 * @param {Array} diffList //存储两树不同的信息,每一项是一个对象，里面表示了不同的类型是增删还是改，还有原始值和修改后的值
 */functiondiffTree(root1, root2, diffList){if(root1 == root2)return diffList;if(root1 ==null&& root2 !=null){//新增
        diffList.push({type:'新增',val1:null,val2: root2
        })}elseif(root1 !=null&& root2 ==null){//删除
        diffList.push({type:'删除',val1: root1,val2:null})}elseif(root1.value != root2.value){//修改:可能只修改这个节点，子节点没有修改，所以需要继续判断比较
        diffList.push({type:'修改',val1: root1,val2: root2
        })diffTree(root1.left, root2.left, diffList);diffTree(root1.right, root2.right, diffList);}else{//往下比较diffTree(root1.left, root2.left, diffList);diffTree(root1.right, root2.right, diffList);}}let diffList =[];diffTree(a1, a2, diffList);
console.log(diffList);

图的最小生成树

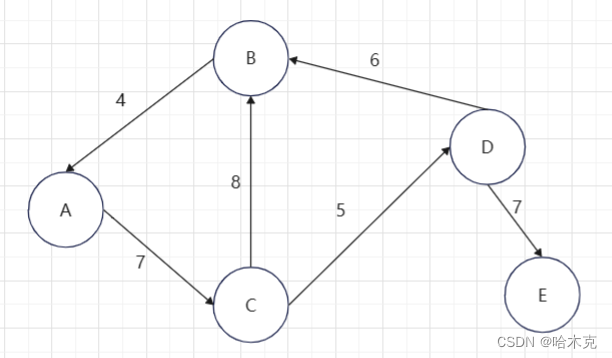
普利姆算法（加点法）

1. 任选一个点作为起点，找到这个点为起点路径最短的边
2. 如果这条边的另一端没有连接，就确定选择这条边
3. 如果这条边两端都连接了，就寻找倒数第二短的边
4. 重复这些步骤将所有的点全部连接

克鲁斯卡尔算法（加边法）

1. 选择一条最短的边进行连接
2. 要保证两端至少有一个点没有连接，除非这两点可以将两个区域连接起来
3. 重复这些步骤将所有的点全部连接

二叉搜索树

有排序效果的二叉树：左子树的节点都比当前节点小，右子树的节点都比当前节点大

functionNode(value){this.value = value;this.left =null;this.right =null;}functionsearchTree(arr){//二叉搜索树if(arr ==null|| arr.length ==0)returnnull;let root =newNode(arr[0]);for(let i =1; i < arr.length; i++){addNode(root, arr[i]);}return root;}functionaddNode(root, num){//将num按大小顺序创建到root的左右子树下if(root ==null)return;if(root.value == num)return;if(num < root.value){//如果num比当前节点小if(root.left ==null) root.left =newNode(num);//左节点不存在则创建elseaddNode(root.left, num);//节点存在继续向左递归比较}else{//如果num比当前节点大if(root.right ==null) root.right =newNode(num);//右节点不存在则创建elseaddNode(root.right, num);//节点存在继续向右递归比较}}

平衡二叉树(AVL)

根节点的左子树和右子树的高度差不能超过1，并且每个子树都符合这一点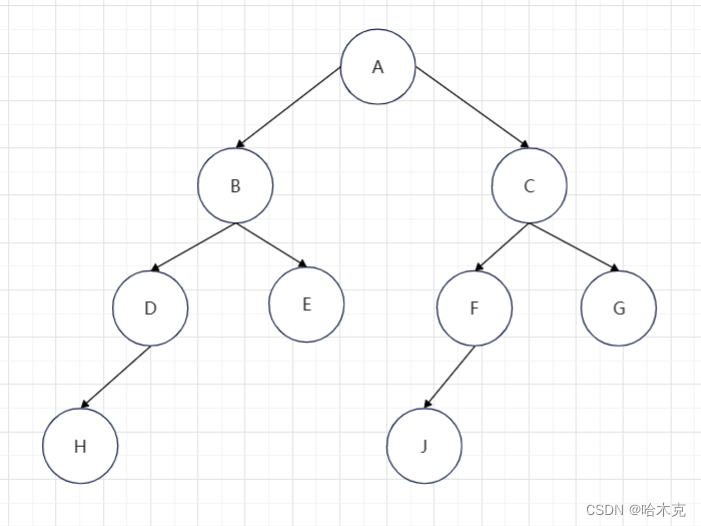

functionNode(value){this.value = value;this.left =null;this.right =null;}let a =newNode("a");let b =newNode("b");let c =newNode("c");let d =newNode("d");let e =newNode("e");let f =newNode("f");let g =newNode("g");let h =newNode("h");let j =newNode("j");

a.left = b;
a.right = c;
b.left = d;
b.right = e;
c.left = f;
c.right = g;
d.right = h;
e.right = j;functiongetDeep(root){//获取二叉树最深层数if(root ==null)return0;let leftDeep =getDeep(root.left);let rightDeep =getDeep(root.right);return Math.max(leftDeep, rightDeep)+1;}functionisBalance(root){//判断是否是平衡二叉树if(root ==null)returntrue;let leftDeep =getDeep(root.left);let rightDeep =getDeep(root.right);if(Math.abs(leftDeep - rightDeep)>1){returnfalse;}else{returnisBalance(root.left)&&isBalance(root.right);}}

二叉树的单旋

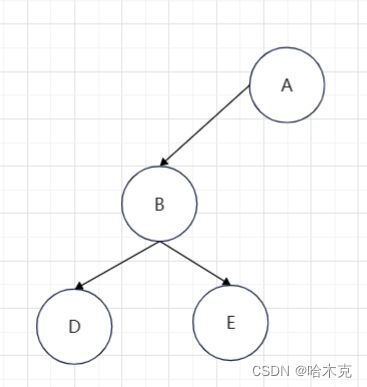
左单旋

• 旋转节点：当前不平衡的节点
• 新根：右子树的根节点
• 变化分支：旋转节点的右子树的左子树
• 不变分支：旋转节点的右子树的右子树

左单旋步骤

1. 找到新根
2. 找到变化分支
3. 旋转节点的右孩子为变化分支
4. 新根的左孩子为旋转节点
5. 返回新根

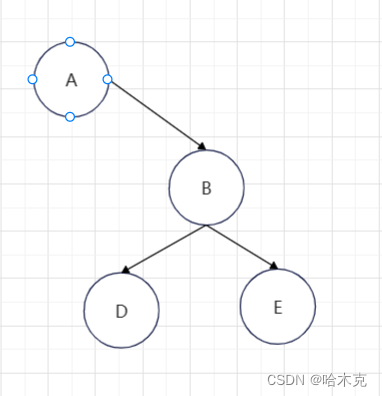
右单旋

• 旋转节点：当前不平衡的节点
• 新根：右子树的根节点
• 变化分支：旋转节点的左子树的右子树
• 不变分支：旋转节点的左子树的左子树

右单旋步骤

1. 找到新根
2. 找到变化分支
3. 旋转节点的左孩子为变化分支
4. 新根的右孩子为旋转节点
5. 返回新根

functionNode(value){this.value = value;this.left =null;this.right =null;}// 左单旋let node1 =newNode('1');let node2 =newNode('3');let node3 =newNode('2');let node4 =newNode('4');
node1.right = node2;
node2.left = node3;
node2.right = node4;// 右单旋let node11 =newNode('6');let node22 =newNode('4');let node33 =newNode('3');let node44 =newNode('5');
node11.left = node22;
node22.left = node33;
node22.right = node44;// 左单旋functionleftRotate(root){// 1. 找到新根let newRoot = root.right;// 2. 找到变化分支let changeRoot = newRoot.left;// 3. 旋转节点的右孩子为变化分支
    root.right = changeRoot;// 4. 新根的左孩子为旋转节点
    newRoot.left = root;// 5. 返回新根return newRoot;}// 右单旋functionrightRotate(root){// 1. 找到新根let newRoot = root.left;// 2. 找到变化分支let changeRoot = newRoot.right;// 3. 旋转节点的左孩子为变化分支
    root.left = changeRoot;// 4. 新根的右孩子为旋转节点
    newRoot.right = root;// 5. 返回新根return newRoot;}

二叉树的双旋

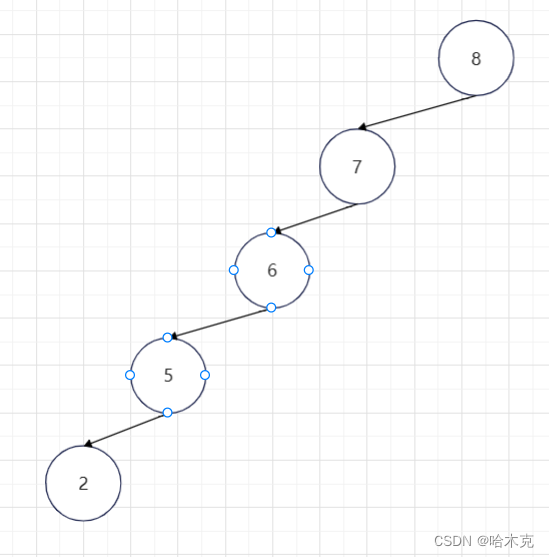
• 左右双旋 当要对某个节点进行右单旋时，如果变化分支是唯一的最深分支， 那么我们要对新根进行左单旋，然后再进行右单旋
• 右左双旋 当要对某个节点进行左单旋时，如果变化分支是唯一的最深分支， 那么我们要对新根进行右单旋，然后再进行左单旋
• 右右双旋、左左双旋 如果变化分支的高度和旋转节点另一侧的高度差距大于2，那么单旋后依旧不平衡，所以需要再次单旋

functionNode(value){this.value = value;this.left =null;this.right =null;}// 双旋let node8 =newNode("8");let node7 =newNode("7");let node6 =newNode("6");let node5 =newNode("5");let node2 =newNode("2");

node8.left = node7;
node7.left = node6;
node6.left = node5;
node5.left = node2;functionchangeBalance(root){//进行单旋操作将二叉树转为平衡二叉树if(isBalance(root))return root;if(root.left !=null) root.left =changeBalance(root.left);if(root.right !=null) root.right =changeBalance(root.right);let leftDeep =getDeep(root.left);let rightDeep =getDeep(root.right);if(Math.abs(leftDeep - rightDeep)<2){return root;}elseif(leftDeep > rightDeep){//右单旋// 左右双旋判断let changeTreeDeep =getDeep(root.left.right);let noChangeTreeDeep =getDeep(root.left.left);if(changeTreeDeep > noChangeTreeDeep){
            root.left =leftRotate(root.left);}// 右右双旋判断let newRoot =rightRotate(root);
        newRoot.right =changeBalance(newRoot.right);
        newRoot =changeBalance(newRoot);return newRoot;}else{//左单旋// 右左双旋判断let changeTreeDeep =getDeep(root.right.left);let noChangeTreeDeep =getDeep(root.right.right);if(changeTreeDeep > noChangeTreeDeep){
            root.right =rightRotate(root.right);}// 左左双旋判断let newRoot =leftRotate(root);
        newRoot.left =changeBalance(newRoot.left);
        newRoot =changeBalance(newRoot);return newRoot;}}

234树

• 我们希望搜索树最多有四叉（度为4），并且每个节点不止存一个值
• 234树的子节点永远在最后一层，234树永远是平衡的（每一条路径的高度都相同）
• 因为分支变多，234树的结构复杂度也上升了，需要进行简化
• 希望简化为二叉树，并且保留多叉，保留一个节点多个值

红黑树

• 节点是红色或黑色
• 根节点是黑色
• 每个红色节点的两个子节点都是黑色
• 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
• 叶节点为黑色（叶节点是指末梢的空节点 Nil或Null）

二叉搜索树、平衡二叉树、红黑树

有了二叉搜索树，为什么还需要平衡二叉树？

1. 二叉搜索树容易退化成一条链，查找的时间复杂度从O(log_{2}N)也将退化成O (N)
2. 引入对左右子树高度差有限制的平衡二叉树，保证查找操作的最坏时间复杂度也为O(log_{2}N)

有了平衡二叉树，为什么还需要红黑树？

1. AVL的左右子树高度差不能超过1，每次进行插入/删除操作时，几乎都需要通过旋转操作保持平衡
2. 在频繁进行插入/删除的场景中，频繁的旋转操作使得AVL的性能大打折扣
3. 红黑树通过牺牲严格的平衡，换取插入/删除时少量的旋转操作，整体性能优于AVL
4. 红黑树插入时的不平衡，不超过两次旋转就可以解决；删除时的不平衡，不超过三次旋转就能解决
5. 红黑树的红黑规则，保证最坏的情况下，也能在O(log_{2}N)时间内完成查找操作

动态规划

斐波那契数列

functionfibonacci(n){let a =0, b =0, c =1;for(let i =1; i <= n;++i){
        a = b;
        b = c;
        c = a + b;}return c;}functionfibonacci2(n){if(n ===1)return0;if(n ===2)return1;returnfibonacci2(n -2)+fibonacci2(n -1);}

青蛙跳台阶

// 青蛙一次可以跳一级台阶或者两级台阶，请问跳到n级台阶有多少种方法// 跳到n级台阶的最后一跳有两种跳法，一是从n-1跳，二是从n-2跳// 我们可以转化成跳到n-1有多少种方法，跳到n-2有多少种方法，相加=跳到n级有多少种方法// f(n) = f(n-1) + f(n-2)functionjumpFloor(n){if(n ===1)return1;if(n ===2)return2;returnjumpFloor(n -1)+jumpFloor(n -2)}// 青蛙一次可以跳一级台阶，两级台阶或者n级台阶，请问跳到n级台阶有多少种方法// f(n) = f(n-1) + f(n-2) + ...... + f(2) + f(1) + f(0)functionjumpFloor2(n){if(n ===1)return1;if(n ===2)return2;let result =0;for(let i =1; i < n; i++){
        result +=jumpFloor2(n - i);}return result +1;//加上直接从0跳到n级的情况}