【Java】四道小题目轻松拿捏位运算（含一道百度面试真题）

文章目录

1. 求一个int类型的整数二进制中1的个数

如：15 0000 1111 4
这道题共有三种解法。

第一种方法：

1. 把这个数右移32次，每次都与上（&）1
2. 每移动一次，判断与后的数字是不是1，是1则计数器+1

原理：

代码如下：

publicstaticintfunc(int n){int count =0;for(int i =0; i <32; i++){//有符号右移或无符号右移都无所谓，//因为已经控制了循环的次数（int类型的二进制一共有32位）if(((n >> i)&1)!=0){
                count++;}}return count;}publicstaticvoidmain(String[] args){int ret =func(-1);System.out.println(ret);}

这种方法的缺点：不论给定的数是否已经计算完毕，都要移动32次，效率不够高。

第二种方法： 在第一种方法的前提下进行优化，减少循环次数

代码：

publicstaticint func1 (int n){int count =0;while(n !=0){if((n &1)!=0){
                count++;}//采用无符号右移的原因：//如果用有符号右移，n是负数的时候每右移一次都会补符号位//每次n的最左边都会补一个1，n永远都不会为0
            n = n >>>1;}return count;}publicstaticvoidmain(String[] args){int ret =func1(-1);System.out.println(ret);}

第二种方法的好处：每次右移完，都会判断一下n是否为0，如果n为0，则说明n的二进制中已经没有1了，也就说明统计结束。

缺点：如果给定的数的二进制是01000000 00000000 00000000 00000000，即使它只有一个1，但依然要循环31次。

第三种方法（最优的方法）：n & (n-1)

我们可以发现，每与一次就会消除n最右边的一个1，只要n不为0，就一直与到n为0。

代码如下：

publicstaticintfunc2(int n){int count =0;while(n !=0){
            count++;
            n &=(n -1);}return count;}publicstaticvoidmain(String[] args){int ret =func2(-1);System.out.println(ret);}

这种方法完美解决了方法二的弊端，再举方法二的例子，n的二进制是
01000000 00000000 00000000 00000000时，只要一次n & (n-1)，便可以结束，即n中有几个1那么就循环几次。

2. 获取一个数二进制序列中所有的偶数位和奇数位，分别输出二进制序列

如7的二进制是 00000000 00000000 00000000 00000111

这道题其实很灵活，奇数位和偶数位是由我们自己来界定的，如果最左边的一位是奇数位，则最右边的一位是偶数位；如果最右边的一位是奇数位，则最左边的一位是奇数位。

这道题我们用后者的情况来学习。

关键在于：

1. 怎么找到每一个位？
2. 怎么判断每一个位上是几？

以7来举例 0000 0111

第一位是1，向右移动2位就得到了第二个奇数位，仔细观察就可以得到如下规律：

偶数位的移动：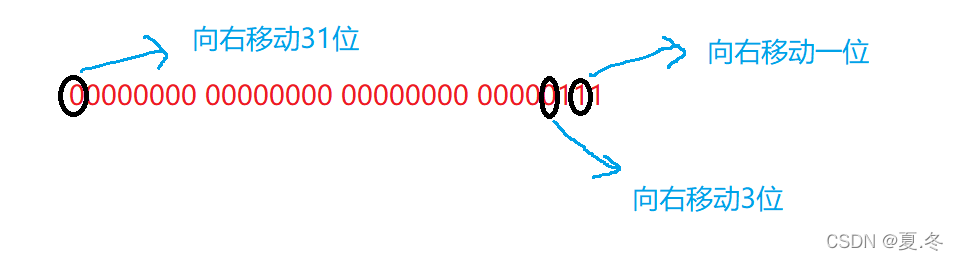

奇数位的移动：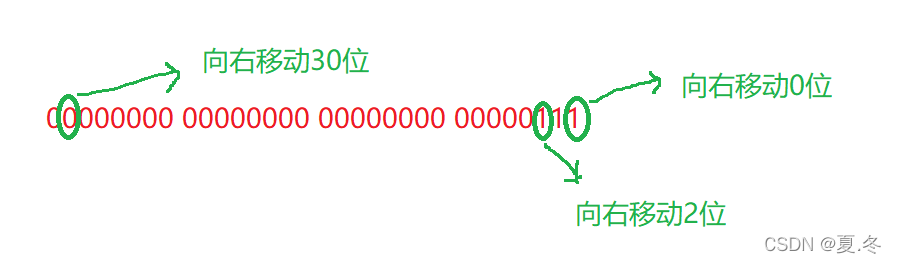

如何判断每一位是几则要用到第一题的方法，即和1做&

我们想按二进制的序列进行打印，则我们要先打印最左边的数字，代码如下：

publicstaticvoidfunc(int n){//打印偶数位for(int i =31; i >=1; i -=2){System.out.print(((n>>i)&1)+" ");}System.out.println();//打印奇数位for(int i =30; i >=0; i -=2){System.out.print(((n>>i)&1)+" ");}}publicstaticvoidmain(String[] args){func(7);}

代码运行结果：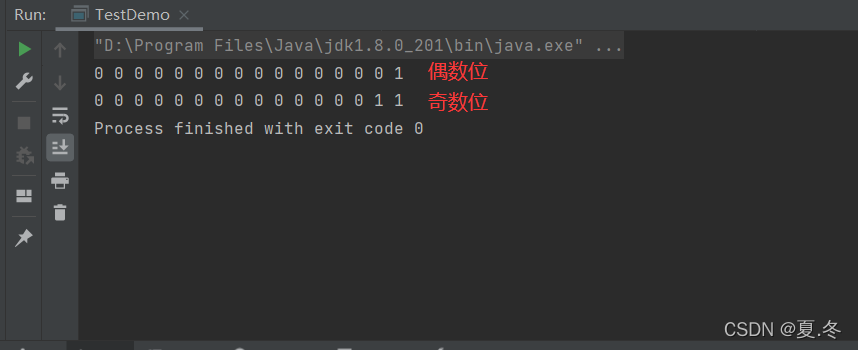

3. 交换两个整数的内容，不允许创建临时变量

我们平时交换两个整数时都是创建一个空瓶子来存储数据，那不允许创建临时变量时又该如何写呢？

publicstaticvoidmain(String[] args){int a =10;int b =20;int tmp =0;
    tmp = a;
    a = b;
    b = tmp;System.out.println(a);System.out.println(b);}

第一种方法：利用加减运算符

代码如下：

publicstaticvoidmain(String[] args){int a =10;int b =20;
    a = a + b;
    b = a - b;
    a = a - b;System.out.println(a);// 20System.out.println(b);// 10}

假设a和b的初始值是A和B

a = a + b // 执行完后 a = A + B, b = B
b = a - b // 即 b = A + B - B = A，执行完后 a = A + B，b = A
a = a - b // 即 a = A + B - A = B，执行完后 a = B，b = A

这样的方法存在一个弊端：当a和b的值很大时，a + b便存在溢出的风险

方法二：利用异或 (^) 操作符

publicstaticvoidmain(String[] args){int a =10;int b =20;
    a = a ^ b;
    b = a ^ b;
    a = a ^ b;System.out.println(a);// 20System.out.println(b);// 10}

在理解这段代码前，我们要学习一个知识：异或是满足交换律的

3 ^ 3 = 0
5 ^ 5 = 0
a ^ a = 0
0 ^ 5 = 5
0 ^ 3 = 3
0 ^ a = a
3 ^ 5 ^ 3 = 3 ^ 3 ^ 5 = 0 ^ 5 = 5

对代码的解析如下：

a = a ^ b // 执行完后，a = a ^ b, b = b
b = a ^ b // 执行完后，a = a ^ b, b = (a ^ b) ^ b
a = a ^ b // 执行完后，a = (a ^ b) ^ (a ^ b ^ b) = a ^ a ^ b ^ b ^ b = 0 ^ b = b
b = a ^ b ^ b = a ^ 0 = a

平时三变量法已经足够好，可以满足我们交换变量的要求，上面两种方法只是为了加深我们对位运算符的理解。

4. 百度面试题：给你一个正整数N，判断这个数是不是2的K次方，不用求K是几

2的0次方 —> 1 —> 0000 0001
2的1次方 —> 2 —> 0000 0010
2的2次方 —> 4 —> 0000 0100
2的3次方 —> 8 —> 0000 1000
2的4次方 —> 16 —> 0001 0000

我们可以发现这些数字的二进制中只有一个1，也就是说：如果二进制中只有一个1，那么它一定是2的K次方

代码如下：

publicstaticbooleanfunc(int n){//用到了第一题的第三种方法来判断其是否只有一个1if((n &(n-1))==0){returntrue;}returnfalse;}publicstaticvoidmain(String[] args){boolean flg =func(256);if(flg){System.out.println("YES");}else{System.out.println("NO");}}

搞定以上四道题后相信大家都对位运算符和二进制有了更深一步的理解，最后期待大家给个三连~~