SGD(Stochastic Gradient Descent)，译为随机梯度下降，是深度学习中的常用的函数优化方法。
1.引例
在介绍
S
G
D
SGD
SGD之前首先来引入一个例子，有三个人在山顶上正在思考如何快速的下山，老大，老二和老三分别提出了三个不同的观点。
- 老大说：从山顶出发，每走一段路程，就寻找附近所有的山路，挑选最陡峭的山路继续前进，顾名思义，老大总是挑最陡峭的山路来走。
- 老二说：从山顶出发，每走一段路程，就随机地寻找附近部分的山路，挑选最陡峭的山路继续前进，顾名思义，老二随机的寻找部分山路，然后走最陡峭的。
- 老三说：从山顶出发，直接随机的挑选山路走，直到到达山脚。
老大的走法虽然每条路都是最优，但是在寻找最陡的山路的过程中会耗费大量的时间。
老二的走法虽然不能保证每次的路都是最优的，但能保证每次的路都比较优，而且不用花费大量的时间来寻找最陡的山路。
老三的走法较为随意，每次走的路有可能最优，可能最劣。![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Vp2WZCwN-1676107686927)(/image_editor_upload/20220730/20220730050337_83545.png)]](https://img-blog.csdnimg.cn/cd88e1f9e1414ad6aacc172da3501320.png)
那么你认为最先到达山脚呢？在学完
S
G
D
SGD
SGD之后，你就会得到答案。
2.SGD介绍
2.1引入问题
给你一个
x
y
xy
xy坐标系，上面有一些点，给你过原点的一条直线
y
=
w
x
y=wx
y=wx，如何用最快的方法来拟合这些点？
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OOYBhgNT-1676107686929)(/image_editor_upload/20220730/20220730050742_20671.png)]](https://img-blog.csdnimg.cn/1c139d76dc4e46538f5b57c99d058e29.png)
为了解决这个问题，我们要对问题定义一个目标，即让所有的点离直线的偏差最小。我们常用的误差函数为均方误差，对于一个点
p
1
p_1
p1来说，它与直线的均方误差可以定义为
e
1
e_1
e1：
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-c26Kyylh-1676107686933)(/image_editor_upload/20220730/20220730050907_67003.png)]](https://img-blog.csdnimg.cn/d73cb59e3f4546e2979394f85acf2950.png)
e
1
=
(
y
1
−
w
x
1
)
2
=
(
w
x
1
−
y
1
)
2
e_1=(y_1-wx_1)^2=(wx_1-y_1)^2
e1=(y1−wx1)2=(wx1−y1)2
完全平方展开：
e
1
=
w
2
x
1
2
−
2
(
w
x
1
y
1
)
+
y
1
2
e_1=w^2{x_1}^2-2(wx_1y_1)+{y_1}^2
e1=w2x12−2(wx1y1)+y12
e
1
=
x
1
2
w
2
−
2
(
x
1
y
1
)
w
+
y
1
2
e_1={x_1}^2w^2-2(x_1y_1)w+{y_1}^2
e1=x12w2−2(x1y1)w+y12
同理，点
p
2
p2
p2，
p
3
p3
p3，
.
.
.
...
...，
p
n
pn
pn都是如此：
e
2
=
x
2
2
w
2
−
2
(
x
2
y
2
)
w
+
y
2
2
e_2={x_2}^2w^2-2(x_2y_2)w+{y_2}^2
e2=x22w2−2(x2y2)w+y22
e
3
=
x
3
2
w
2
−
2
(
x
3
y
3
)
w
+
y
3
2
e_3={x_3}^2w^2-2(x_3y_3)w+{y_3}^2
e3=x32w2−2(x3y3)w+y32
e
n
=
x
n
2
w
2
−
2
(
x
n
y
n
)
w
+
y
n
2
e_n={x_n}^2w^2-2(x_ny_n)w+{y_n}^2
en=xn2w2−2(xnyn)w+yn2
而我们最终的误差
e
=
(
∑
e
1
+
e
2
+
.
.
.
+
e
n
)
/
n
e=(\sum{e_1+e_2+...+e_n})/n
e=(∑e1+e2+...+en)/n
通过合并同类项：![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TEdFVq6M-1676107686938)(/image_editor_upload/20220730/20220730033337_23748.png)]](https://img-blog.csdnimg.cn/d78d423e6408413bba2b513bba03300a.png)
最终得到：![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-O3OoFB8m-1676107686942)(/image_editor_upload/20220730/20220730033844_37099.png)]](https://img-blog.csdnimg.cn/52781acac4aa4897b798ab85e6dfef29.png)
因为
a
=
x
1
2
+
.
.
.
+
x
n
2
a={x_1}^2+...+{x_n}^2
a=x12+...+xn2，所以
a
>
0
a>0
a>0，所以
e
e
e是一个向上的抛物线。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KEOyQ3GV-1676107686945)(/image_editor_upload/20220730/20220730035607_63923.png)]](https://img-blog.csdnimg.cn/9e5ec7dde7214ef299005925442ba375.png)
定义好误差函数后，可以开始计算梯度了![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XAaZ1Nsf-1676107686948)(/image_editor_upload/20220730/20220730040028_16349.png)]](https://img-blog.csdnimg.cn/0559b1d796be421db9be548a77bdf3b1.png)
显然，当达到
e
w
ew
ew图像中的最低点的时候，
e
e
e最小，此时的
w
w
w最优。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9Z6I2XFP-1676107686951)(/image_editor_upload/20220730/20220730041214_11905.png)]](https://img-blog.csdnimg.cn/4c17849a9bd841599c55b4e3f1d71643.png)
如何从右边黄色的点快速移到最低处呢？这就是随机梯度下降了，从自身位置出发，每隔一段路程就探索一次，随机挑选一个梯度最大的方向进行移动，直到移动到最低点。
那隔多远进行探索一次呢？这就是学习率
l
e
a
r
n
i
n
g
learning
learning
r
a
t
e
rate
rate了，当
l
e
a
r
n
i
n
g
learning
learning
r
a
t
e
=
0.1
rate=0.1
rate=0.1时
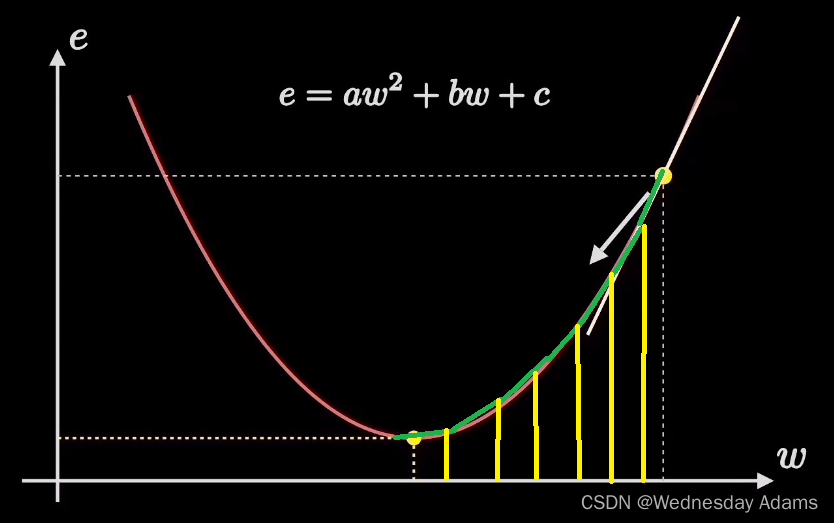
当
l
e
a
r
n
i
n
g
learning
learning
r
a
t
e
=
0.2
rate=0.2
rate=0.2时
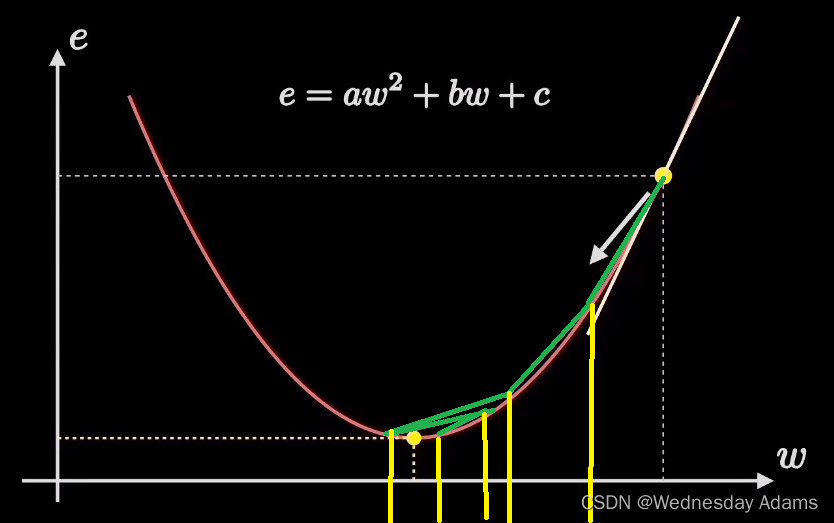
好的学习率能够让点快速降到最低
2.2SGD的计算步骤
回到刚刚爬山那个问题，通过大量数据实验得知，老二的
S
G
D
SGD
SGD方法能最快到达山脚。
3.SGD的代码实现
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
X_scaler = StandardScaler()
y_scaler = StandardScaler()
X =[[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300]]
y =[[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330]]#plt.show()
X = X_scaler.fit_transform(X)#用什么方法标准化数据？
y = y_scaler.fit_transform(y)
X_test =[[40],[400]]# 用来做最终效果测试
X_test = X_scaler.transform(X_test)
model = SGDRegressor()
model.fit(X, y.ravel())
y_result = model.predict(X_test)
plt.title('single variable')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.plot(X, y,'k.')
plt.plot(X_test, y_result,'g-')
plt.show()
结果：![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DvmfgnmY-1676107686960)(/image_editor_upload/20220730/20220730050240_27787.png)]](https://img-blog.csdnimg.cn/106bdd7315024542af7b41fa4876aebb.png)
本文转载自: https://blog.csdn.net/qq_55126913/article/details/128986125
版权归原作者 Wednesday Adams 所有， 如有侵权，请联系我们删除。
版权归原作者 Wednesday Adams 所有， 如有侵权，请联系我们删除。