【数据结构】二叉搜索树剖析（附源码）

文章目录

前言

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势；所以应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。
–百度百科

一、什么是二叉搜索树？

为什么会有二叉搜索树的结构？
在大型的查找集合当中进行动态查找的时候，假设用顺序存储（数组），如果不要求记录存储的有序性，那么插入操作的平均查找时间是O（N）。提高效率的方法是把插入的节点进行排序，这样折半查找的效率为O(logN)，但是插入需要O(N)的时间。
解决方案：将查找集合组织成树结构（称为“树表”）能够很好的实现动态查找，二叉排序树就是一种常见的树表。

二叉排序树的性质：
1.若左子树不空，则左子树上的所有节点均小于根节点的值。
2.若右子树不空，则右子树上的所有节点的值均大于根节点的值。
3.左右子树都是二叉排序树。

二、编写代码

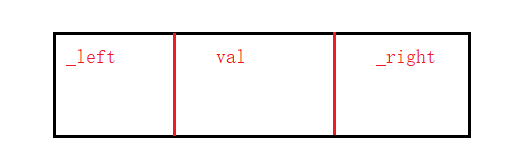
节点结构，每个节点由左右指针和一个值val构成。

template<classK>structBSTreeNode{public:BSTreeNode(const K& val =K()):_left(nullptr),_right(nullptr),_val(val){}

    BSTreeNode<K>* _left;
    BSTreeNode<K>* _right;
    K _val;};

1、二叉排序树的插入

我们这里实现的是不允许键值冗余的版本，插入节点需要注意：

• 插入节点一定是插入值为NULL节点的位置
• 插入节点后记得父节点要与插入节点连接
• 插入的节点比当前节点大往右子树走，反之往左子树走，相等返回false(插入失败)

非递归版本：

boolInsert(const K& val){//找NULL节点插入if(!_root){
            _root =newNode(val);returntrue;}
        Node* newnode =newNode(val);
        Node* parent =nullptr;
        Node* cur = _root;while(cur){if(cur->_val < val){
                parent = cur;
                cur = cur->_right;}elseif(cur->_val == val){//实现的不允许键值冗余returnfalse;}else{
                parent = cur;
                cur = cur->_left;}}//插入节点与父节点相连if(parent->_val > val){
            parent->_left = newnode;}else{
            parent->_right = newnode;}returntrue;}

递归版本：
外层的InsertR是给外层调用的，由于递归要有头结点，所以我们设置子函数_InsertR来完成递归。

以插入节点{63,55}为栗子，叙述一下传引用的妙用：

• 参数传引用Node*& root是一大妙用，上面栗子，我们拿插入63与55为例，当插入63的时候，由于root是_root 的引用，那么相当于_root = new Node(val)。而插入55的时候，这个时候不需要再让父节点的指针链接，是因为_InsertR(root->_left, val);root是上一层root->_left的引用，相当于站在上一层来看，root->_left = new Node(val)，这个用法是很不错的。当然若是理解不了，可以再传多一个参数来记录父指针。
• 迭代版本不使用引用是因为使用引用头结点会改变头结点的位置，而递归当中不会改变头结点的位置。

bool_InsertR(Node*& root,const K& val){//传引用的妙用if(root ==nullptr){
            root =newNode(val);returntrue;}if(root->_val < val){return_InsertR(root->_right, val);}elseif(root->_val > val){return_InsertR(root->_left, val);}else{returnfalse;}}boolInsertR(const K& val){//子问题：往子树上插入return_InsertR(_root, val);}

2、二叉搜索树的遍历

我们通常遍历二叉树使用中序遍历，因为遍历出来的结果恰好是升序的，我们这里可以用一个Inorder函数来验证我们插入节点是否有没有编写正确。
这里我们用递归遍历，编写起来简单。
递归版本：

void_Inorder(Node* root){if(root ==nullptr)return;_Inorder(root->_left);
        cout << root->_val <<" ";_Inorder(root->_right);}voidInorder(){_Inorder(_root);
        cout << endl;}

3、二叉树的查找

由二叉搜索树的本身性质，我们要查找一个树的时候最多走O(logN)高度，当我们走到NULL节点前还没有找到该节点，就表示查找失败。

• 查找遍历树的逻辑与插入类似，比较简单，不做叙述。非递归版本：

Node*Find(const K& val){
        Node* cur = _root;while(cur){if(cur->_val < val){
                cur = cur->_right;}elseif(cur->_val > val){
                cur = cur->_left;}else{return cur;//查找成功}}returnnullptr;//查找失败}

递归版本：

• 这里root没必要传引用，要传也可以。

    Node*FindR(Node* root,const K& val){if(root ==nullptr){returnfalse;}if(val < root->_val){FindR(root->_left, val);}elseif(val > root->_val){FindR(root->_right, val);}else{return root;}}
    Node*FindR(const K& val){returnFindR(_root, val);}

4、二叉排序树的删除（难）

二叉排序树的删除分为以下几种情况：

• 情况1：删除的节点有左右孩子，1.1、这种情况我们通常采用伪删除的方式，我们可以在该节点的右子树找最小节点或者该节点的左子树找最大节点来代替，再删除这个替换上来的节点。1.2、以用右子树的最小孩子来替换为例，注意该情况还分为右孩子的最左孩子不为NULL（右子树的最小节点），和右孩子的最左孩子为NULL的两种情况。
• 情况2：删除的节点只有左孩子/右孩子，让父亲指向该节点的左孩子/右孩子。
• 情况3：删除的节点没有孩子，父亲的原先指向该节点的指针置为NULL。
• 情况4：删除的节点是情况2或情况3+删除的是头结点。

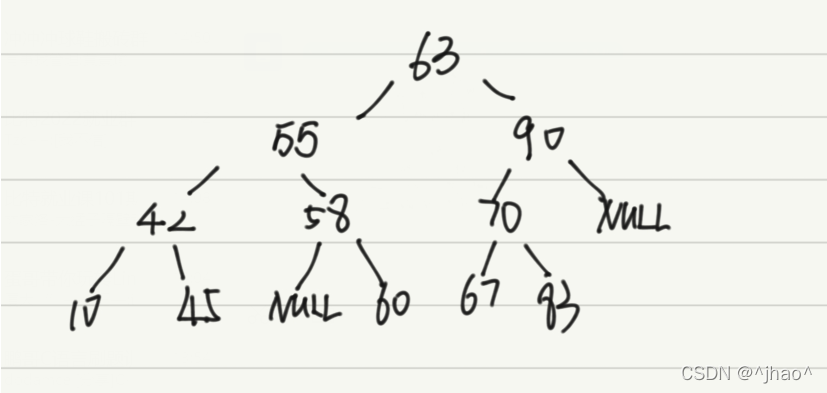
用一个例子将上面几种情况都解释一下，假设现有一颗{63,55,90,42,58,60，70,10,42,67,83}的树。

下面图中红色圈起来为要删除节点，绿色圈起来为替换节点

情况一 ：我们以删除63为例：
1. 要找到替换的节点，我们就要找到90这颗子树的最小节点，再递归下去就是找到70这颗子树的最小节点…也就是最终的67这个节点，然后我们可以覆盖式的修改63。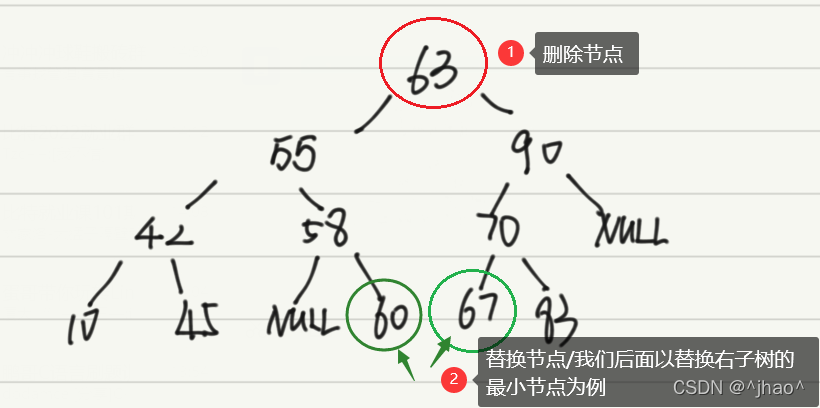

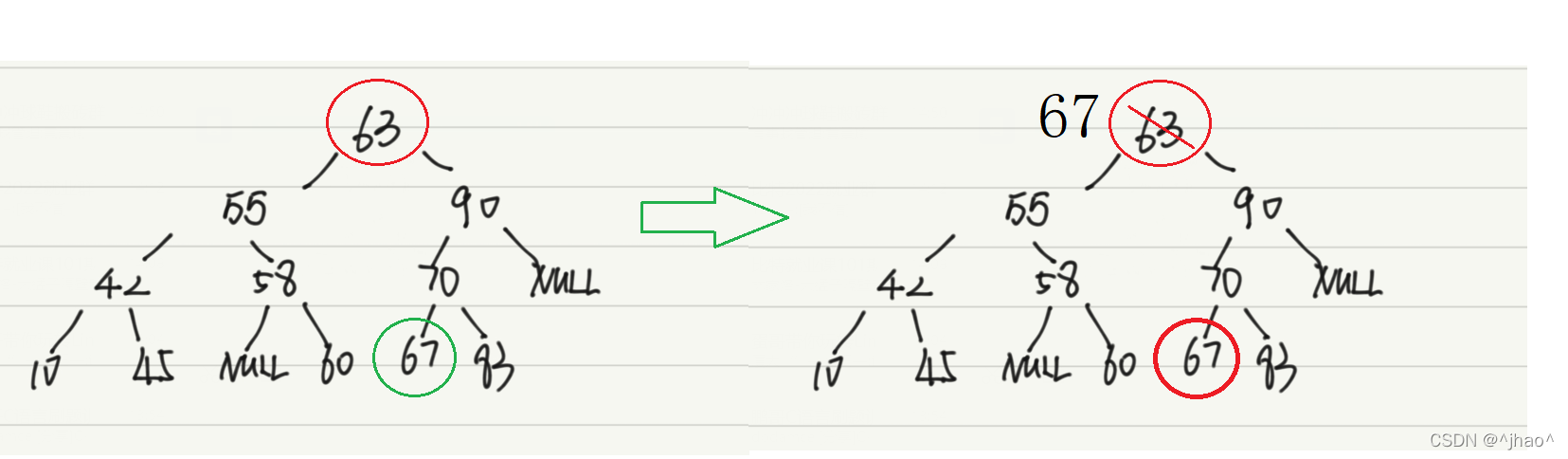
2. 然后我们把问题就可以缩小成为，删除底下的67节点，这个节点一定具备只有右孩子/或没有孩子节点，也就是情况2和情况3，而这两种情况都可以合成一种解决方案：
让被删除节点67（最底下的67）的父节点（70）的左孩子指针指向67的右孩子。

情况一 第二种情况：
删除55的情况：
这也是左右孩子都有的情况，但和前一个例子不同，它的替换节点就是它的右孩子，这个时候要删除，对于新的要删除58节点，它的删除方式就是让父节点58的右孩子指针指向它的右孩子。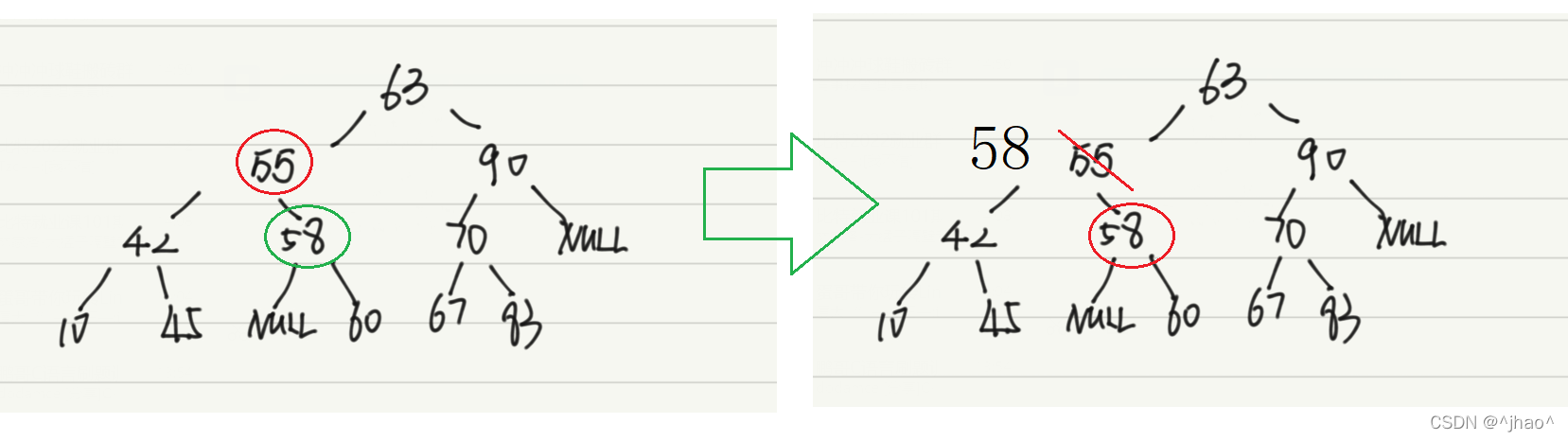

情况二：
删除90的情况：
我们可以用父节点的右孩子指针指向70即可，注意：倘若删除节点在父节点的什么位置，就让父节点对应的左右指针指向删除节点的非空节点。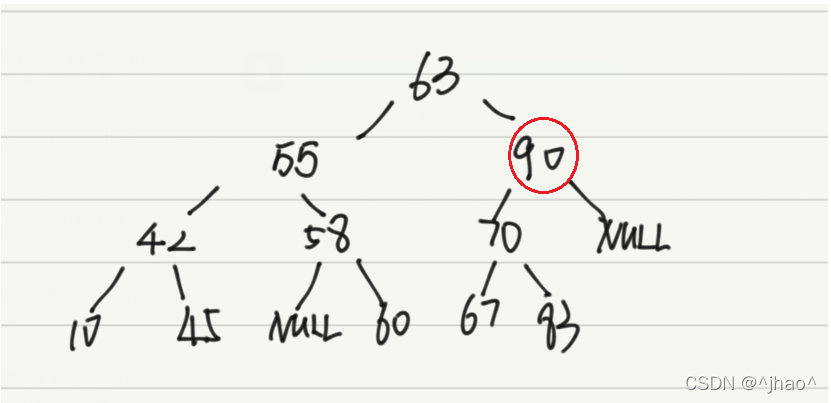

情况三：
删除83的情况：虽然把他单独分类成一种情况，但是它是可以用情况二的逻辑去处理的，让70判断83在左还是右子树，然后在用指针指向83的左孩子或者右孩子都可以。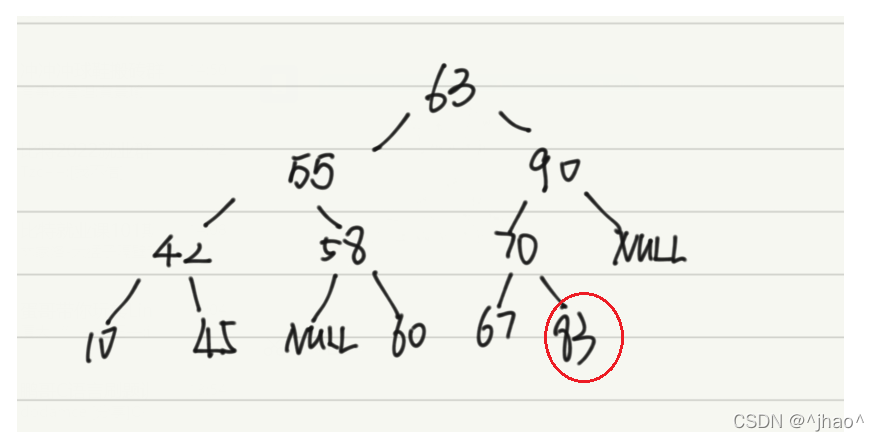

情况四：
以{1,2，3,4}为例子，当我们删除1的时候：
倘若按照情况二的方式处理，那么我们会有一个parent为NULL，并且链接2的情况，所以实际上我们要在情况二的条件判断加多一个parent指针是否为NULL的情况。
解决方案：实际上让删除节点的左或者右孩子成为新的头结点就可以了。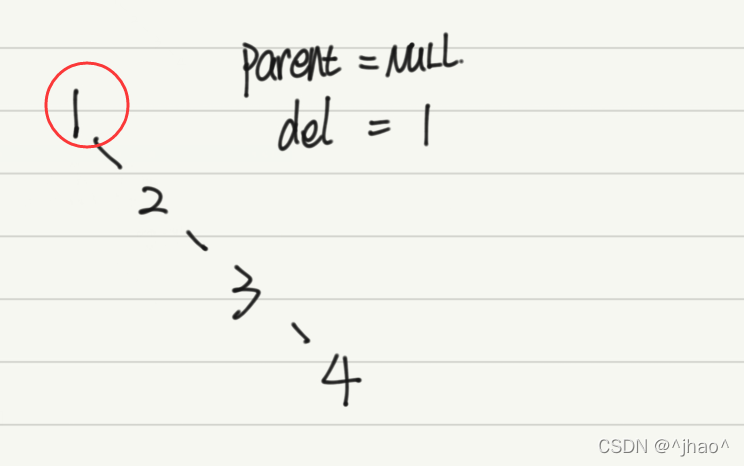

非递归版本：
代码对各种情况进行了标识，结合上图理解。

voidDeleteNode(const K& val){if(_root ==nullptr)return;//删除前先找到该节点 
        Node* parent =nullptr;
        Node* cur = _root;while(cur){if(cur->_val < val){
                parent = cur;
                cur = cur->_right;}elseif(cur->_val > val){
                parent = cur;
                cur = cur->_left;}else{break;}}if(cur ==nullptr)return;//找不到该节点//对该节点的三种状态进行判断//情况2或情况3**if(cur->_left ==nullptr){//情况4**//特殊：删除头结点--> if(cur == _root){
                _root = cur->_right;}elseif(cur == parent->_left){
                parent->_left = cur->_right;}else{
                parent->_right = cur->_right;}delete cur;}elseif(cur->_right ==nullptr){if(cur == _root){
                _root = cur->_left;}elseif(cur == parent->_left){
                parent->_left = cur->_left;}else{
                parent->_right = cur->_left;}delete cur;}else{//这里是不涉及parent指针的解引用行为，所以不用考虑更换头结点//左右两个节点都存在//分两种：右孩子就是最小/和不是最小//情况1** 
            Node* delParent = cur;
            Node* delcur = cur;
            delcur = delcur->_right;while(delcur->_left){
                delParent = delcur;//找右子树的最小和左子树最大都可以
                delcur = delcur->_left;}if(delParent == cur){//1.1swap(delcur->_val, delParent->_val);
                cur->_right = delcur->_right;delete delcur;}else{//1.2swap(cur->_val, delcur->_val);
                delParent->_left = delcur->_right;delete delcur;}}}

递归版本：
递归版本采用头结点传引用有妙用

对于情况1，我们可以将情况划分，当我们在删除63的时候，实际上可以划分为将67赋值给63，并且在90这颗子树里面删除67
对于情况2/3，传引用我们就可以不需要头结点了，因为后面传参的节点都是前面的引用。
对于情况4，在传引用的情况下，实际上也解决了。

情况1图解：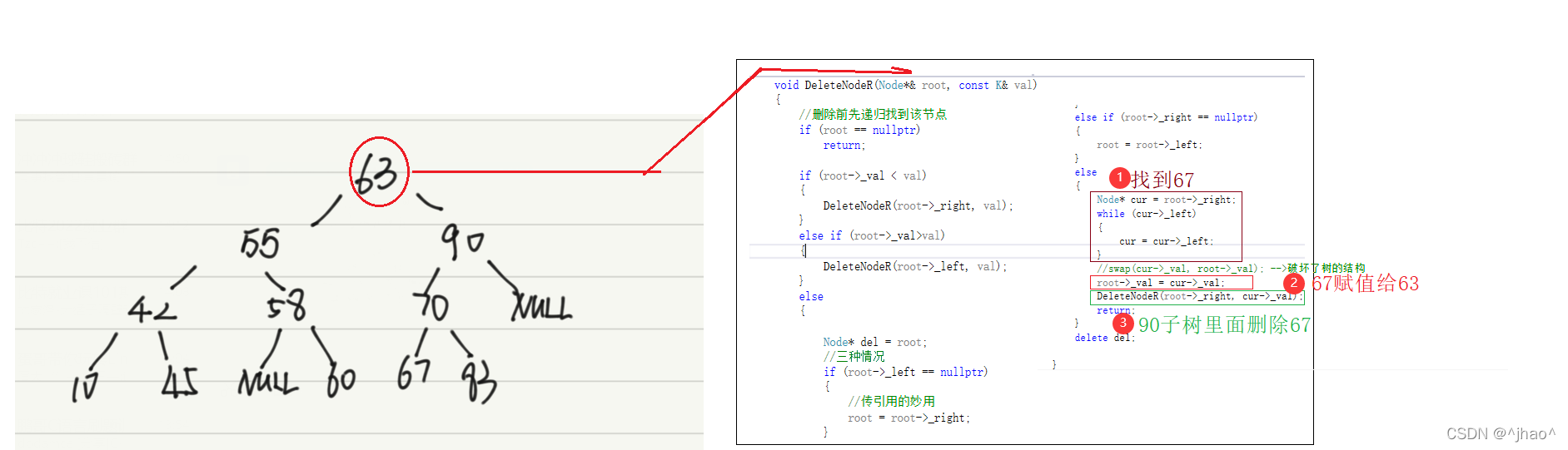

情况2/3图解：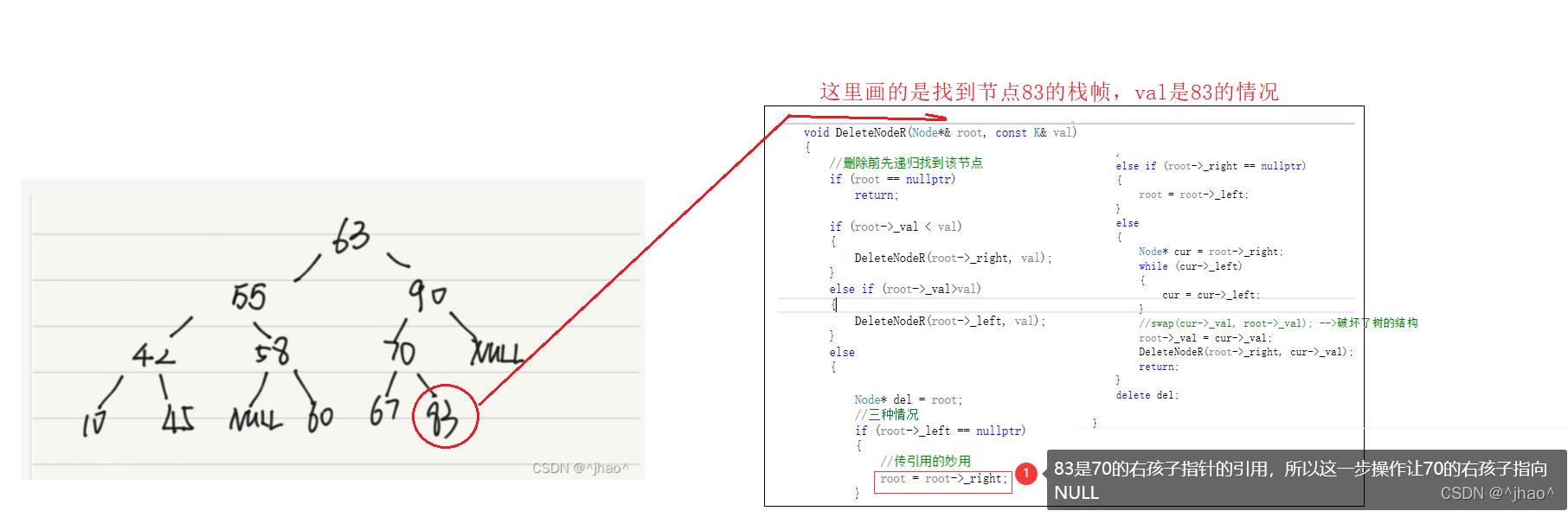

情况4图解：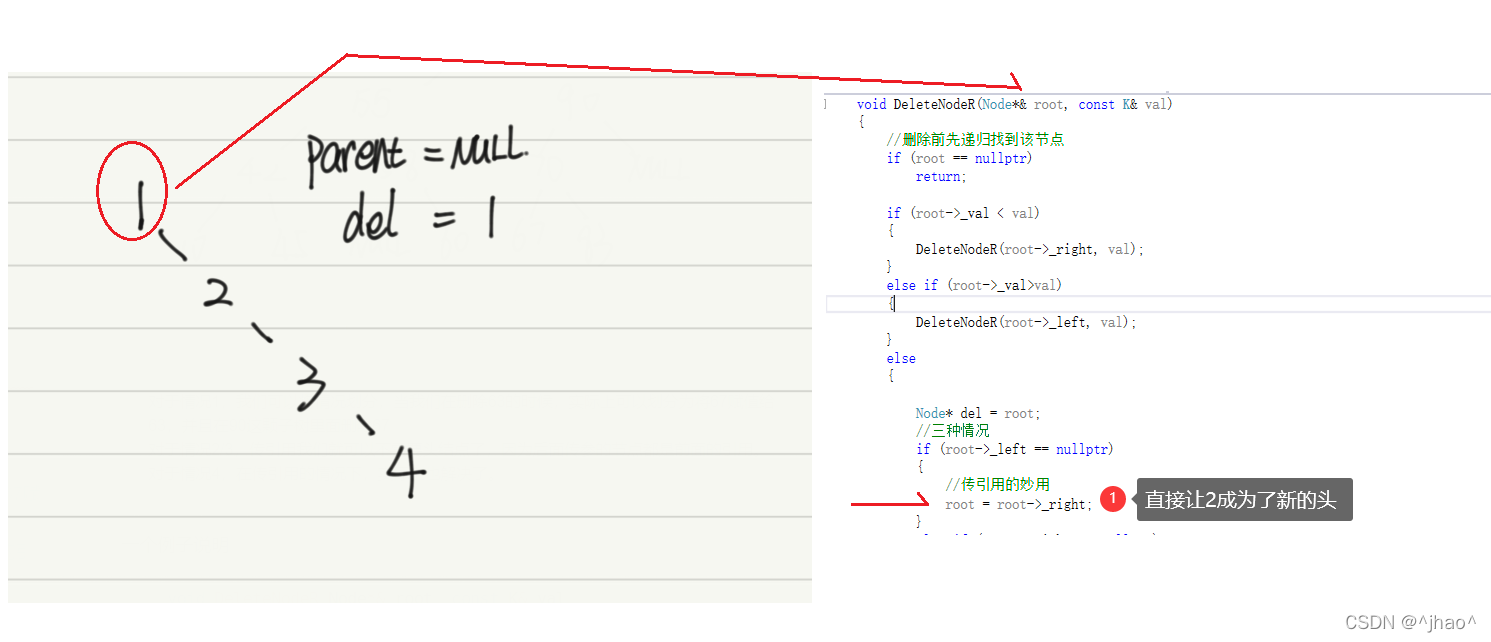

voidDeleteNodeR(Node*& root,const K& val){//删除前先递归找到该节点if(root ==nullptr)return;if(root->_val < val){DeleteNodeR(root->_right, val);}elseif(root->_val>val){DeleteNodeR(root->_left, val);}else{
            Node* del = root;if(root->_left ==nullptr){//情况2/3/4//传引用的妙用
                root = root->_right;}elseif(root->_right ==nullptr){//情况2/3/4
                root = root->_left;}else{//情况1
                Node* cur = root->_right;while(cur->_left){
                    cur = cur->_left;}//swap(cur->_val, root->_val); -->破坏了树的结构
                root->_val = cur->_val;DeleteNodeR(root->_right, cur->_val);return;}delete del;}}voidDeleteNodeR(const K& val){DeleteNodeR(_root, val);}

总结：
虽然都递归的写法要比迭代的写法要短，但是我们发现若在情况1当中，我们找到了替换节点，实际上一步就可以把他删除（迭代写法一步就删除了），但是采用递归的话又需要重新在子树当中去找到新的删除的节点，所以实际上没有迭代的写法优。
ps:
并且递归的弊端还有：栈帧的开销，栈溢出的危险。

5.默认成员函数编写

5.1、构造函数

//构造函数BSTree()=default;

5.2、拷贝构造

拷贝构造当中我们用先序遍历的递归构造一颗树。

BSTree(const BSTree<K>& bs)//const BSTree& bs

：默认成员函数中的传参可以不指定模板类型。

//拷贝构造
    Node*Copy(Node* copyroot){if(copyroot ==nullptr)returnnullptr;

        Node* root =newNode(copyroot->_val);
        root->_left =Copy(copyroot->_left);
        root->_right =Copy(copyroot->_right);return root;}BSTree(const BSTree<K>& bs)//const BSTree& bs{
        _root =Copy(bs._root);}

5.3、赋值重载

这里用现代写法，临时对象tmp进行拷贝构造后将头结点交换给当前的对象，然后顺手将当前对象的搜索二叉树的节点给清理了。

//赋值重载
    BSTree&operator=(const BSTree<K>& bs){if(&bs !=this){
            BSTree tmp(bs);swap(tmp._root,this->_root);}return*this;}

5.4、析构函数

采用后序遍历的方式进行节点的释放，因为后序遍历的规则是左右根，只有当当前节点的左子树和右子树的节点释放完才会释放当前节点，这样就保证了释放当前节点后不会需要当前节点递归到下一个要释放的节点。

//析构函数voidDestroy(Node* root){if(root ==nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}~BSTree(){Destroy(_root);}

三、性能分析

二叉搜索树的查找最小比较次数为1次，最多比较高度次数，所以树的形态直接影响二叉排序树的操作效率，对于具有n个节点的二叉排序树，查找性能在O(logN)下取整+1 ~ O(N)之间。

总结

难点在于删除，删除可以多看看，以及对于传引用的理解。