NNDL 实验五前馈神经网络（1）二分类任务

4.1 神经元

4.1.1 净活性值

使用pytorch计算一组输入的净活性值𝑧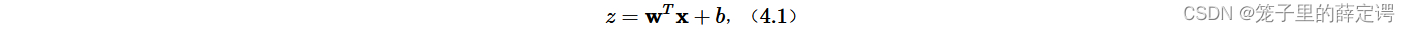
在这里插入图片描述使用Pytorch计算一组输入的净活性值。代码实现如下：

import torch

# 2个特征数为5的样本
X = torch.rand([2,5])# 含有5个参数的权重向量
w = torch.rand([5,1])# 偏置项
b = torch.rand([1,1])# 使用'torch.matmul'实现矩阵相乘
z = torch.matmul(X, w)+ b
print("input X:", X)print("weight w:", w,"\nbias b:", b)print("output z:", z)

运行结果：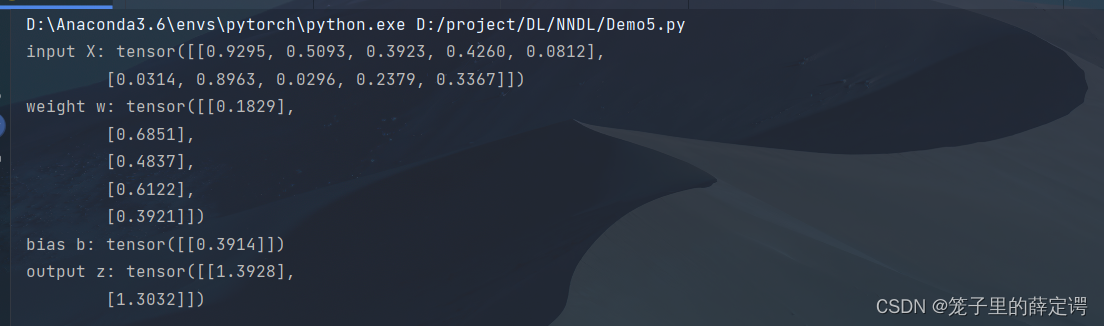
在这里插入图片描述 torch.nn.Linear()函数实现：

import torch
import torch.nn as nn
from torch.autograd import Variable

m = nn.Linear(5,1)input= Variable(torch.rand(2,5))#包装Tensor使得支持自动微分
output = m(input)print(output)

运行结果：
在这里插入图片描述 torch.nn.Linear()的使用:

classtorch.nn.Linear（in_features，out_features，bias =True ）

作用

对传入数据应用线性变换：y = A x+ b

参数

in_features - 每个输入样本的大小
out_features - 每个输出样本的大小
bias - 如果设置为False，则图层不会学习附加偏差。默认值：True

具体举例如上.

学习pytorch不会查pytorch文档可不行，下面是pytorch官网的截图:
在这里插入图片描述注:如上所示,需要注意的一点是torch.nn.Linear（）层只支持TensorFloat32类型

官方文档的链接：
Pytorch官方文档

思考题

加权求和与仿射变换之间有什么区别和联系？
简单来说，而加权和就是对输入的信息进行线性变换，仿射变换就是线性变换+平移。
1.从实践角度来看
加权和(线性变换)的形式如下：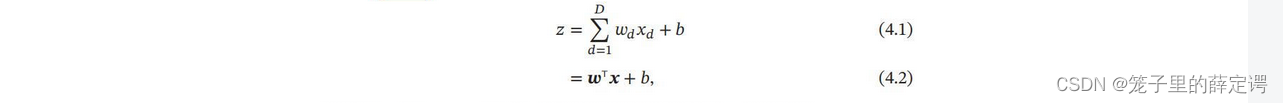
在这里插入图片描述再附上一张老师找给我们关于仿射变换的图：
仿射变换与线性变换的联系如下：
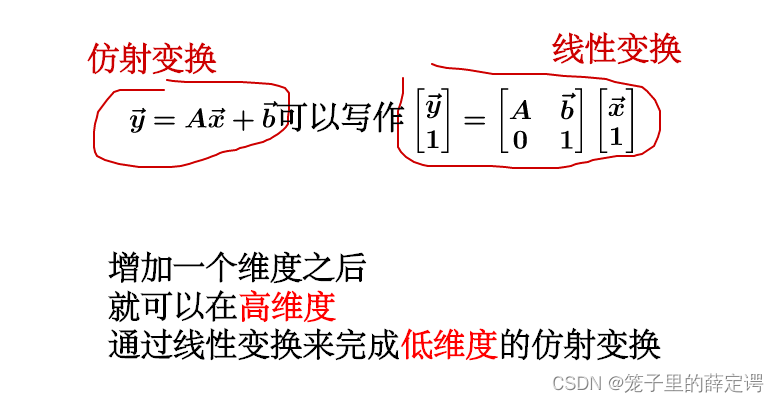下面是老师找的关于加权求和与仿射变换的讲解图：

2.从数学角度来看

加权和(线性变换)从几何直观有三个要点：

变换前是直线的，变换后依然是直线
直线比例保持不变变换前是原点的
变换后依然是原点

仿射变换从几何直观只有两个要点：

变换前是直线的
变换后依然是直线直线比例保持不变

少了原点保持不变这一条。

很直观的就是仿射变换不仅仅包括线性变换，而且包含剪切和反射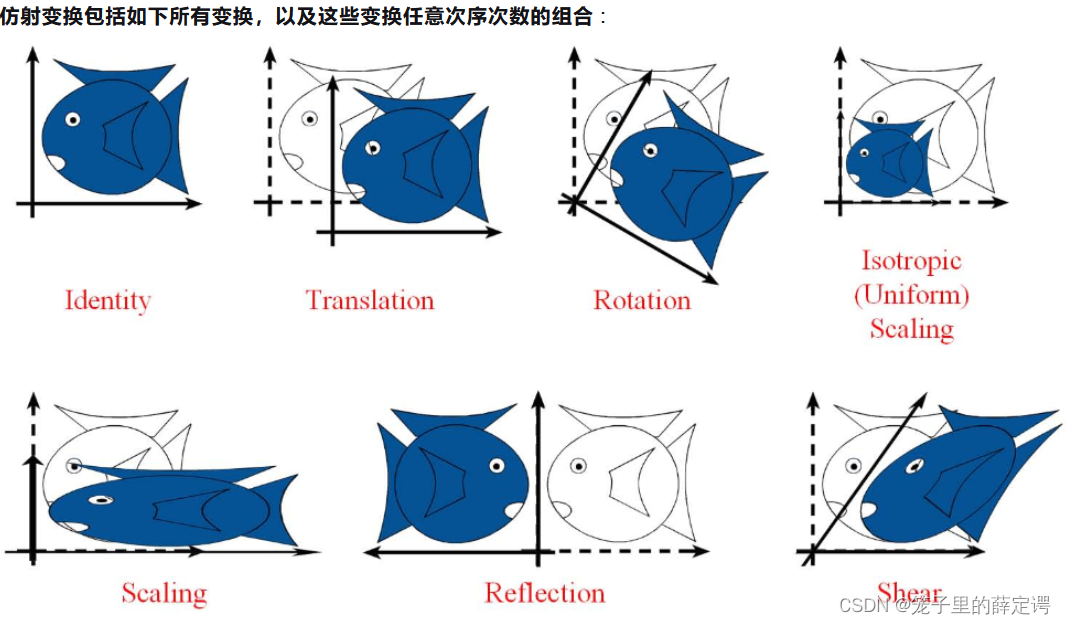
在这里插入图片描述

4.1.2 激活函数

净活性值z再经过一个非线性函数f(⋅)后，得到神经元的活性值a。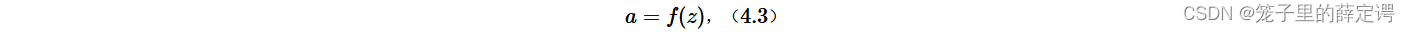
在这里插入图片描述激活函数通常为非线性函数，可以增强神经网络的表示能力和学习能力。
常用的激活函数有S型函数和ReLU函数。

4.1.2.1 Sigmoid 型函数

1.使用python实现并可视化“Logistic函数、Tanh函数”

import torch
import matplotlib.pyplot as plt

# Logistic函数deflogistic(z):return1.0/(1.0+ torch.exp(-z))# Tanh函数deftanh(z):return(torch.exp(z)- torch.exp(-z))/(torch.exp(z)+ torch.exp(-z))# 在[-10,10]的范围内生成10000个输入值，用于绘制函数曲线
z = torch.linspace(-10,10,10000)

plt.figure()
plt.plot(z.tolist(), logistic(z).tolist(), color='#e4007f', label="Logistic Function")
plt.plot(z.tolist(), tanh(z).tolist(), color='#f19ec2', linestyle ='--', label="Tanh Function")

ax = plt.gca()# 获取轴，默认有4个# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')# 调整坐标轴位置   
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')
plt.show()

运行结果：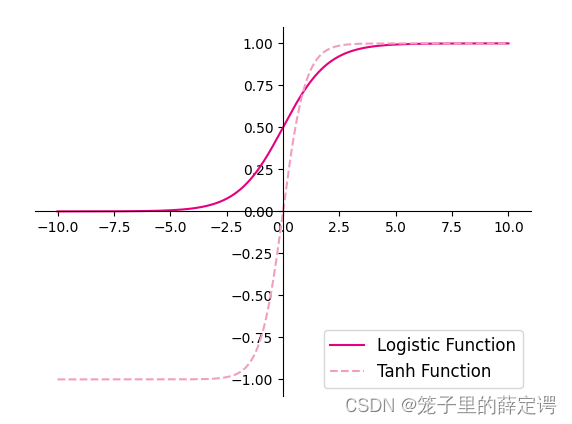
在这里插入图片描述

2.在pytorch中找到相应函数并测试。

import torch
import matplotlib.pyplot as plt

# 在[-10,10]的范围内生成10000个输入值，用于绘制函数曲线
z = torch.linspace(-10,10,10000)

plt.figure()
plt.plot(z.tolist(), torch.sigmoid(z).tolist(), color='#ff0077', label="Logistic Function")
plt.plot(z.tolist(), torch.tanh(z).tolist(), color='#ff0077', linestyle ='--', label="Tanh Function")

ax = plt.gca()# 获取轴，默认有4个# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')# 调整坐标轴位置   
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')
plt.show()

运行结果：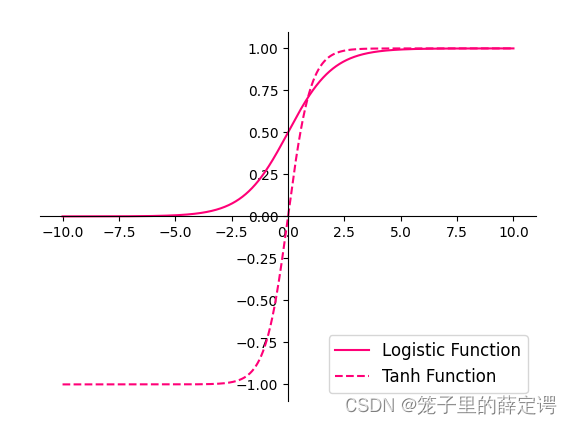
在这里插入图片描述

4.1.2.2 ReLU型函数

常见的ReLU函数有ReLU和带泄露的ReLU（Leaky ReLU）

1.使用python实现并可视化可视化“ReLU、带泄露的ReLU的函数”

import torch
import matplotlib.pyplot as plt

# ReLUdefrelu(z):return torch.maximum(z, torch.as_tensor(0.))# 带泄露的ReLUdefleaky_relu(z, negative_slope=0.1):# 当前版本torch暂不支持直接将bool类型转成int类型，因此调用了torch的cast函数来进行显式转换
    a1 =(torch.can_cast((z >0).dtype, torch.float32)* z)
    a2 =(torch.can_cast((z <=0).dtype, torch.float32)*(negative_slope * z))return a1 + a2

# 在[-10,10]的范围内生成一系列的输入值，用于绘制relu、leaky_relu的函数曲线
z = torch.linspace(-10,10,10000)

plt.figure()
plt.plot(z.tolist(), relu(z).tolist(), color="#e4007f", label="ReLU Function")
plt.plot(z.tolist(), leaky_relu(z).tolist(), color="#f19ec2", linestyle="--", label="LeakyReLU Function")

ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('fw-relu-leakyrelu.pdf')
plt.show()

运行结果：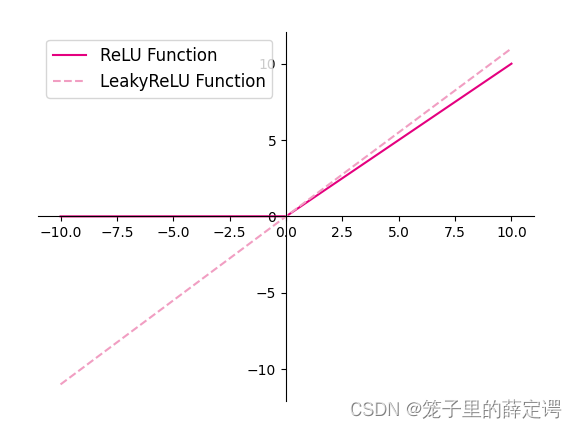
在这里插入图片描述
2.在pytorch中找到相应函数并测试。

import torch
import matplotlib.pyplot as plt

# 在[-10,10]的范围内生成一系列的输入值，用于绘制relu、leaky_relu的函数曲线
z = torch.linspace(-10,10,10000)

plt.figure()
plt.plot(z.tolist(), torch.relu(z).tolist(), color="#e4007f", label="ReLU Function")
plt.plot(z.tolist(), torch.nn.LeakyReLU(0.1)(z), color="#f19ec2", linestyle="--", label="LeakyReLU Function")

ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('fw-relu-leakyrelu.pdf')
plt.show()

运行结果：
![在这里插入图片描述](https://img-blog.csdnimg.cn/1c3e52db401045e8ab8f6b172ecd5c5e.png

4.2 基于前馈神经网络的二分类任务

4.2.1 数据集构建

使用第3.1.1节中构建的二分类数据集：Moon1000数据集，其中训练集640条、验证集160条、测试集200条。该数据集的数据是从两个带噪音的弯月形状数据分布中采样得到，每个样本包含2个特征。

from nndl.dataset import make_moons
# 采样1000个样本
n_samples =1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.5)

num_train =640
num_dev =160
num_test =200

X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]

y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])

运行结果：
在这里插入图片描述

注:nndl.dataset.make_moons如下：

import torch
import math
import numpy as np
# 新增make_moons函数defmake_moons(n_samples=1000, shuffle=True, noise=None):
    n_samples_out = n_samples //2
    n_samples_in = n_samples - n_samples_out

    outer_circ_x = torch.cos(torch.linspace(0, math.pi, n_samples_out))
    outer_circ_y = torch.sin(torch.linspace(0, math.pi, n_samples_out))

    inner_circ_x =1- torch.cos(torch.linspace(0, math.pi, n_samples_in))
    inner_circ_y =0.5- torch.sin(torch.linspace(0, math.pi, n_samples_in))print('outer_circ_x.shape:', outer_circ_x.shape,'outer_circ_y.shape:', outer_circ_y.shape)print('inner_circ_x.shape:', inner_circ_x.shape,'inner_circ_y.shape:', inner_circ_y.shape)

    X = torch.stack([torch.cat([outer_circ_x, inner_circ_x]),
         torch.cat([outer_circ_y, inner_circ_y])],
         axis=1)print('after concat shape:', torch.cat([outer_circ_x, inner_circ_x]).shape)print('X shape:', X.shape)# 使用'torch. zeros'将第一类数据的标签全部设置为0# 使用'torch. ones'将第一类数据的标签全部设置为1
    y = torch.cat([torch.zeros([n_samples_out]), torch.ones([n_samples_in])])print('y shape:', y.shape)# 如果shuffle为True，将所有数据打乱if shuffle:# 使用'torch.randperm'生成一个数值在0到X.shape[0]，随机排列的一维Tensor做索引值，用于打乱数据
        idx = torch.randperm(X.shape[0])
        X = X[idx]
        y = y[idx]# 如果noise不为None，则给特征值加入噪声if noise isnotNone:
        X += np.random.normal(0.0, noise, X.shape)return X, y

4.2.2 模型构建

为了更高效的构建前馈神经网络，我们先定义每一层的算子，然后再通过算子组合构建整个前馈神经网络。

4.2.2.1 线性层算子

from nndl.op import Op

# 实现线性层算子classLinear(Op):def__init__(self, input_size, output_size, name, weight_init=np.random.standard_normal, bias_init=torch.zeros):

        self.params ={}# 初始化权重
        self.params['W']= weight_init([input_size, output_size])
        self.params['W']= torch.as_tensor(self.params['W'],dtype=torch.float32)# 初始化偏置
        self.params['b']= bias_init([1, output_size])
        self.inputs =None

        self.name = name

    defforward(self, inputs):
        self.inputs = inputs

        outputs = torch.matmul(self.inputs, self.params['W'])+ self.params['b']return outputs

Op=Op
注:nndl.op.Op如下：

classOp(object):def__init__(self):passdef__call__(self, inputs):return self.forward(inputs)defforward(self, inputs):raise NotImplementedError

    defbackward(self, inputs):raise NotImplementedError

4.2.2.2 Logistic算子`

classLogistic(Op):def__init__(self):
        self.inputs =None
        self.outputs =Nonedefforward(self, inputs):

        outputs =1.0/(1.0+ torch.exp(-inputs))
        self.outputs = outputs
        return outputs

4.2.2.3 层的串行组合

实现一个两层的用于二分类任务的前馈神经网络，选用Logistic作为激活函数，利用上面实现的线性层和激活函数算子来组装

# 实现一个两层前馈神经网络classModel_MLP_L2(Op):def__init__(self, input_size, hidden_size, output_size):
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()def__call__(self, X):return self.forward(X)defforward(self, X):
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)return a2

实例化一个两层的前馈网络，令其输入层维度为5，隐藏层维度为10，输出层维度为1。
并随机生成一条长度为5的数据输入两层神经网络，观察输出结果。

# 实例化模型
model = Model_MLP_L2(input_size=5, hidden_size=10, output_size=1)# 随机生成1条长度为5的数据
X = torch.rand([1,5])
result = model(X)print("result: ", result)

运行结果：
在这里插入图片描述

4.2.3 损失函数

# 实现交叉熵损失函数classBinaryCrossEntropyLoss(op.Op):def__init__(self):
        self.predicts =None
        self.labels =None
        self.num =Nonedef__call__(self, predicts, labels):return self.forward(predicts, labels)defforward(self, predicts, labels):
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss =-1./ self.num *(torch.matmul(self.labels.t(), torch.log(self.predicts))+ torch.matmul((1-self.labels.t()), torch.log(1-self.predicts)))
        loss = torch.squeeze(loss, axis=1)return loss

4.2.4 模型优化

神经网络的层数通常比较深，其梯度计算和上一章中的线性分类模型的不同的点在于：

线性模型通常比较简单可以直接计算梯度，而神经网络相当于一个复合函数，需要利用链式法则进行反向传播来计算梯度。

4.2.4.1 反向传播算法

第1步是前向计算，可以利用算子的forward()方法来实现；
第2步是反向计算梯度，可以利用算子的backward()方法来实现；
第3步中的计算参数梯度也放到backward()中实现，更新参数放到另外的优化器中专门进行。

4.2.4.2 损失函数

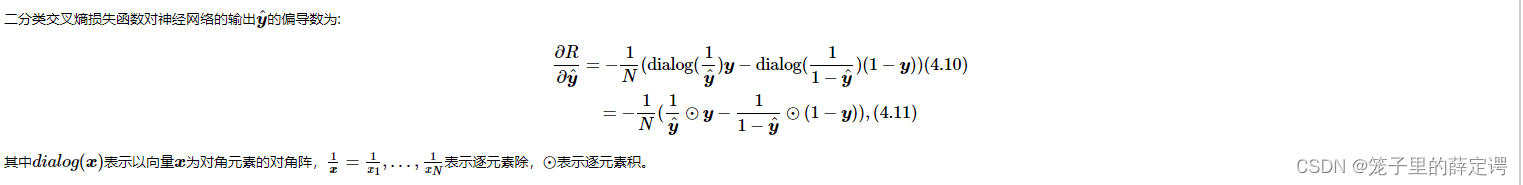
二分类交叉熵损失函数

实现损失函数的backward()：

# 实现交叉熵损失函数classBinaryCrossEntropyLoss(Op):def__init__(self, model):
        self.predicts =None
        self.labels =None
        self.num =None

        self.model = model

    def__call__(self, predicts, labels):return self.forward(predicts, labels)defforward(self, predicts, labels):

        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss =-1./ self.num *(torch.matmul(self.labels.t(), torch.log(self.predicts))+ torch.matmul((1- self.labels.t()), torch.log(1- self.predicts)))

        loss = torch.squeeze(loss, axis=1)return loss

    defbackward(self):# 计算损失函数对模型预测的导数
        loss_grad_predicts =-1.0*(self.labels / self.predicts -(1- self.labels)/(1- self.predicts))/ self.num

        # 梯度反向传播
        self.model.backward(loss_grad_predicts)

4.2.4.3 Logistic算子

为Logistic算子增加反向函数

classLogistic(Op):def__init__(self):
        self.inputs =None
        self.outputs =None
        self.params =Nonedefforward(self, inputs):
        outputs =1.0/(1.0+ torch.exp(-inputs))
        self.outputs = outputs
        return outputs

    defbackward(self, grads):# 计算Logistic激活函数对输入的导数
        outputs_grad_inputs = torch.multiply(self.outputs,(1.0- self.outputs))return torch.multiply(grads,outputs_grad_inputs)

4.2.4.4 线性层

线性层输入的梯度
代码实现如下：

classLinear(Op):def__init__(self, input_size, output_size, name, weight_init=np.random.standard_normal, bias_init=torch.zeros):
        self.params ={}
        self.params['W']= weight_init([input_size, output_size])
        self.params['W']= torch.as_tensor(self.params['W'],dtype=torch.float32)
        self.params['b']= bias_init([1, output_size])

        self.inputs =None
        self.grads ={}

        self.name = name

    defforward(self, inputs):
        self.inputs = inputs
        outputs = torch.matmul(self.inputs, self.params['W'])+ self.params['b']return outputs

    defbackward(self, grads):
        self.grads['W']= torch.matmul(self.inputs.T, grads)
        self.grads['b']= torch.sum(grads, dim=0)# 线性层输入的梯度return torch.matmul(grads, self.params['W'].T)

4.2.4.5 整个网络

实现完整的两层神经网络的前向和反向计算

classModel_MLP_L2(Op):def__init__(self, input_size, hidden_size, output_size):# 线性层
        self.fc1 = Linear(input_size, hidden_size, name="fc1")# Logistic激活函数层
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

        self.layers =[self.fc1, self.act_fn1, self.fc2, self.act_fn2]def__call__(self, X):return self.forward(X)# 前向计算defforward(self, X):
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)return a2

    # 反向计算defbackward(self, loss_grad_a2):
        loss_grad_z2 = self.act_fn2.backward(loss_grad_a2)
        loss_grad_a1 = self.fc2.backward(loss_grad_z2)
        loss_grad_z1 = self.act_fn1.backward(loss_grad_a1)
        loss_grad_inputs = self.fc1.backward(loss_grad_z1)

4.2.4.6 优化器

在计算好神经网络参数的梯度之后，我们将梯度下降法中参数的更新过程实现在优化器中。

与第3章中实现的梯度下降优化器SimpleBatchGD不同的是，此处的优化器需要遍历每层，对每层的参数分别做更新。

from nndl.opitimizer import Optimizer

classBatchGD(Optimizer):def__init__(self, init_lr, model):super(BatchGD, self).__init__(init_lr=init_lr, model=model)defstep(self):# 参数更新for layer in self.model.layers:# 遍历所有层ifisinstance(layer.params,dict):for key in layer.params.keys():
                    layer.params[key]= layer.params[key]- self.init_lr * layer.grads[key]

注：nndl.opitimizer.Optimizer如下：

from abc import abstractmethod
#新增优化器基类classOptimizer(object):def__init__(self, init_lr, model):#初始化学习率，用于参数更新的计算
        self.init_lr = init_lr
        #指定优化器需要优化的模型
        self.model = model

    @abstractmethoddefstep(self):pass

4.2.5 完善Runner类：RunnerV2_1

1.支持自定义算子的梯度计算，在训练过程中调用self.loss_fn.backward()从损失函数开始反向计算梯度；
2.每层的模型保存和加载，将每一层的参数分别进行保存和加载。

classRunnerV2_1(object):def__init__(self, model, optimizer, metric, loss_fn,**kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores =[]
        self.dev_scores =[]# 记录训练过程中的评价指标变化情况
        self.train_loss =[]
        self.dev_loss =[]deftrain(self, train_set, dev_set,**kwargs):# 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs",0)# 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs",100)# 传入模型保存路径
        save_dir = kwargs.get("save_dir",None)# 记录全局最优指标
        best_score =0# 进行num_epochs轮训练for epoch inrange(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)# 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)# return a tensor

            self.train_loss.append(trn_loss.item())# 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)

            self.loss_fn.backward()# 参数更新
            self.optimizer.step()

            dev_score, dev_loss = self.evaluate(dev_set)# 如果当前指标为最优指标，保存该模型if dev_score > best_score:print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
                if save_dir:
                    self.save_model(save_dir)if log_epochs and epoch % log_epochs ==0:print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")defevaluate(self, data_set):
        X, y = data_set
        # 计算模型输出
        logits = self.model(X)# 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)# 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)return score, loss

    defpredict(self, X):return self.model(X)defsave_model(self, save_dir):# 对模型每层参数分别进行保存，保存文件名称与该层名称相同for layer in self.model.layers:# 遍历所有层ifisinstance(layer.params,dict):
               torch.save(layer.params, os.path.join(save_dir, layer.name+".pdparams"))defload_model(self, model_dir):# 获取所有层参数名称和保存路径之间的对应关系
        model_file_names = os.listdir(model_dir)
        name_file_dict ={}for file_name in model_file_names:
            name = file_name.replace(".pdparams","")
            name_file_dict[name]= os.path.join(model_dir, file_name)# 加载每层参数for layer in self.model.layers:# 遍历所有层ifisinstance(layer.params,dict):
                name = layer.name
                file_path = name_file_dict[name]
                layer.params = torch.load(file_path)

注:我把上面模型保存路径改成了相对路径，方便模型的保存，不容易报错。

4.2.6 模型训练

使用训练集和验证集进行模型训练，共训练2000个epoch。评价指标为accuracy。

epoch_num =1000

model_saved_dir ='D:\project\DL\Lenet\logs'# 输入层维度为2
input_size =2# 隐藏层维度为5
hidden_size =5# 输出层维度为1
output_size =1# 定义网络
model = Model_MLP_L2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)# 损失函数
loss_fn = BinaryCrossEntropyLoss(model)# 优化器
learning_rate =0.2
optimizer = BatchGD(learning_rate, model)# 评价方法
metric = accuracy

# 实例化RunnerV2_1类，并传入训练配置
runner = RunnerV2_1(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train],[X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_dir=model_saved_dir)

注:这里你记得修改你的目录名称，我为了方便直接找了个之前的日志文件夹放进去训练好的模型。

（epoch_num = 1000,lr = 0.2）运行结果：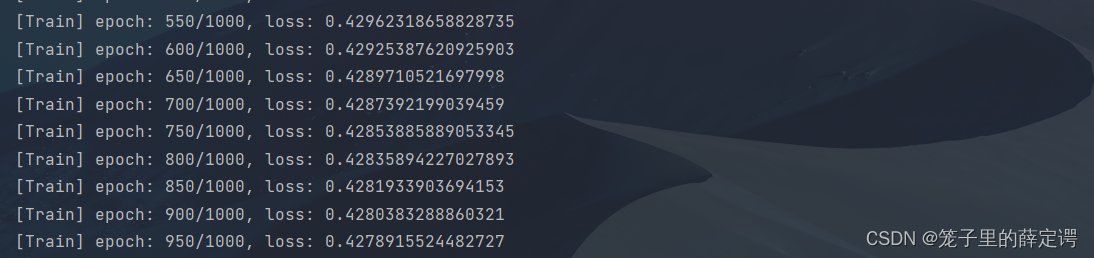
在这里插入图片描述（epoch_num = 1000,lr = 0.002）运行结果：

在这里插入图片描述注: 可以看到Train loss下降，但是Test loss也有微小的下降趋于不变，具体是网络正在学习还是模型达到过拟合状态需要拉大epoch进一步看看效果。
（epoch_num = 10000,lr = 0.002）运行结果：

注: 彻底把网络跑成过拟合状态，说明上面的结果不是网络正在学习而是过拟合状态

（epoch_num = 1000,lr = 2）运行结果：
在这里插入图片描述注：train loss下降，Test loss上升，虽然不那么明显，但也说明此时网络已经达到欠拟合状态(网络结构非常简单，对比得出的效果不是那么明显。)
附上我的笔记图：
请添加图片描述

可视化观察训练集与验证集的损失函数变化情况。

import matplotlib.pyplot as plt
# 打印训练集和验证集的损失
plt.figure()
plt.plot(range(epoch_num), runner.train_loss, color="#e4007f", label="Train loss")
plt.plot(range(epoch_num), runner.dev_loss, color="#f19ec2", linestyle='--', label="Dev loss")
plt.xlabel("epoch", fontsize='large')
plt.ylabel("loss", fontsize='large')
plt.legend(fontsize='x-large')
plt.show()#加载训练好的模型
runner.load_model(model_saved_dir)# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])

运行结果：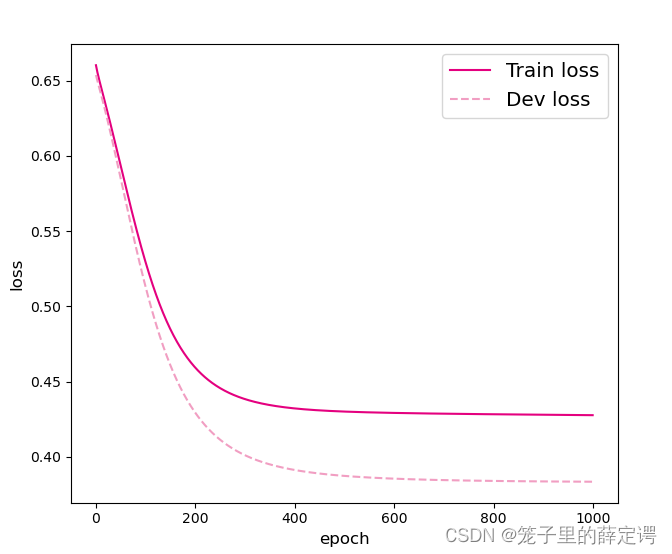
在这里插入图片描述

4.2.7 性能评价

# 加载训练好的模型
runner.load_model(model_saved_dir)# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

运行结果：
在这里插入图片描述下面对结果进行可视化：

import math

# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-math.pi, math.pi,200), torch.linspace(-math.pi, math.pi,200))

x = torch.stack([torch.flatten(x1), torch.flatten(x2)], axis=1)# 预测对应类别
y = runner.predict(x)# y = torch.squeeze(torch.as_tensor(torch.can_cast((y>=0.5).dtype,torch.float32)))# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:,0].tolist(), x[:,1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)

plt.scatter(X_train[:,0].tolist(), X_train[:,1].tolist(), marker='*', c=torch.squeeze(y_train,axis=-1).tolist())
plt.scatter(X_dev[:,0].tolist(), X_dev[:,1].tolist(), marker='*', c=torch.squeeze(y_dev,axis=-1).tolist())
plt.scatter(X_test[:,0].tolist(), X_test[:,1].tolist(), marker='*', c=torch.squeeze(y_test,axis=-1).tolist())

plt.show()

运行结果：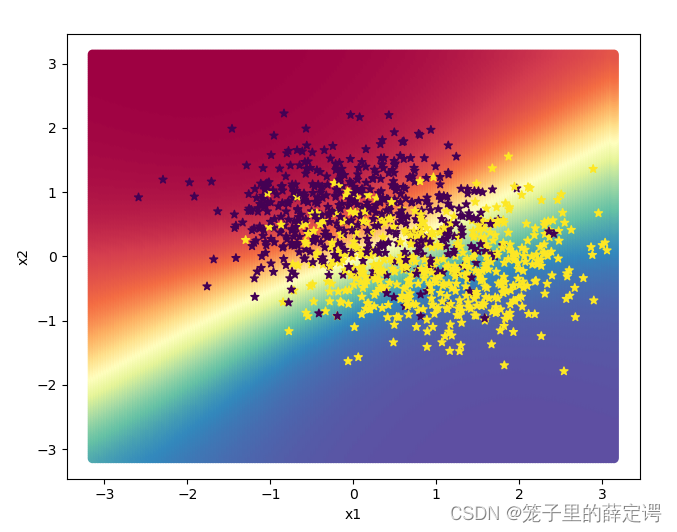
在这里插入图片描述

思考题

对比 3.1 基于Logistic回归的二分类任务 4.2 基于前馈神经网络的二分类任务

第一点即上文提到的：线性模型通常比较简单可以直接计算梯度，而神经网络相当于一个复合函数，需要利用链式法则进行反向传播来计算梯度，并且从保存模型的时候就可以看出前馈神经网络的参数量要大于logistic的参数量。

第二点：自己感觉使用logisitic激活函数的前馈神经网络和基于Logisitic回归的二分类任务差不太多，我觉得不同点可能是前馈神经网络扩展性更强一点，毕竟这次实验前馈神经网络只搭建了两层，搭更深后可能在相同的数据集上前馈神经网络的性能表现更好一些，就比如深度前馈神经网络VGG相比AlexNet并没有太多的改进，其最主要的意义就是实践了“神经网络越深越好”的理念。

(基于Logisitic回归的二分类任务测试集表现图)

在这里插入图片描述 (基于前馈神经网络的二分类任务测试集表现图)

可以看出前馈神经网络比Logisitic回归性能还是好很多的。

第三点：这一点就和这两次做的实验没关系了，主要是数学建模中的模型应用，比如数学建模选择模型的过程中，会参考数据量的多少，数据量少肯定选择Logisitic回归模型，数据量大两个都可以，但是数据量越大，训练神经网络得到的结果越好。

总结

1.这次主要做的工作是搭建了一个两层的前馈神经网络，工作量较小，但是在保存模型的时候一直报错(因为这次需要保存的模型文件是一个文件夹，而不是一个文件，已经把解决方案贴到参考文献里了)，打算这周把后面实验也趁热打铁做一下。
2.清楚了加权求和与仿射变换数学与深度学习方面的区别与联系,总结了一下Logistic回归模型与前馈神经网络的对比，发现还是前馈神经网络的性能更好一些。

参考文献

注：这次学习一下参考文献的写法

[1]陈舜华,吕纯濂.前馈神经网络和Logit回归的比较研究[J].数学的实践与认识,2002(03):374-386.

[2]邱锡鹏.《神经网络与深度学习》[J].中文信息学报,2020,34(07):4.

参考链接

Pytorch官方文档(入门必查)
Python torch.nn.LeakyReLU用法及代码示例
PermissionError: [Errno 13] Permission denied: 问题的解决方法（这个就是我保存模型报错时的解决方案）

如何通俗地讲解「仿射变换」这个概念？
仿射变换及其变换矩阵的理解

NNDL 实验五前馈神经网络（1）二分类任务（老师布置作业的链接）

标签：神经网络分类深度学习

本文转载自: https://blog.csdn.net/liuzi_hang/article/details/127045192
版权归原作者 笼子里的薛定谔 所有，如有侵权，请联系我们删除。

NNDL 实验五前馈神经网络（1）二分类任务