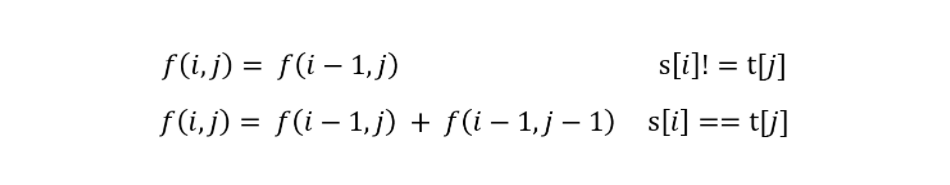LeetCode 剑指 Offer II 动态规划（三） 专题总结

• 📚 博客主页：⭐️这是一只小逸白的博客鸭~⭐️
• 👉 欢迎 关注❤️点赞👍收藏⭐️评论📝
• 😜 小逸白正在备战实习，经常更新面试题和LeetCode题解，欢迎志同道合的朋友互相交流~
• 💙 若有问题请指正，记得关注哦，感谢~

往期文章 ：

• LeetCode 剑指 Offer II 排序 专题总结
• LeetCode 剑指 Offer II 回溯(上) 专题总结
• LeetCode 剑指 Offer II 回溯(下) 专题总结
• LeetCode 剑指 Offer II 动态规划（一） 专题总结
• LeetCode 剑指 Offer II 动态规划（二） 专题总结

目录

097. 子序列的数目

题目：

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。
字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"

ACE

" 是 “

ABCDE

” 的一个子序列，而 “

AEC

” 不是）
题目数据保证答案符合 32 位带符号整数范围。

示例：

输入：s = “rabbbit”, t = “rabbit”
输出：3
解释：
如下图所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。
rabbbit
rabbbit
rabbbit

提示：

• 0 <= s.length, t.length <= 1000
• s 和 t 由英文字母组成

思路：

因为该问题输入为两个字符串，所以状态方程需要两个变量。设 f(i, j) 表示字符串 s 下标从 0 到 i 的子字符串 s[0] ~ s[i] 中等于字符串 t 下标从 0 到 j 的子字符串 t[0] ~ t[j] 的子序列个数。因为若字符串 s 的长度小于字符串 t，那么字符串 s 中肯定不可能存在子字符串使其等于字符串 t，所以当 i < j 时 f(i, j) = 0。当 i >= j 时，若 s[i] != t[j] ，那么无法用 s[i] 去匹配 t[i] 则需要舍去 s[i]，可以得到 f(i, j) = f(i - 1, j)， 表示 s[0] ~ s[i] 中与 t[0] ~ t[j] 相等的子序列个数与s[0] ~ s[i - 1] 中与 t[0] ~ t[j] 相等的子序列个数相同。若 s[i] == t[j]，则既可以舍去 s[i] 不进行匹配也可以使用 s[i] 与 t[j] 进行匹配，可以得到 f(i, j) = f(i - 1, j) + f(i - 1, j - 1)，f(i - 1, j) 表示不进行匹配时的个数，f(i - 1, j - 1) 表示进行匹配的个数，其值代表字符串 s[0] ~ s[i - 1] 中与字符串 t[0] ~ t[j - 1] 相等的子序列个数。故转移方程

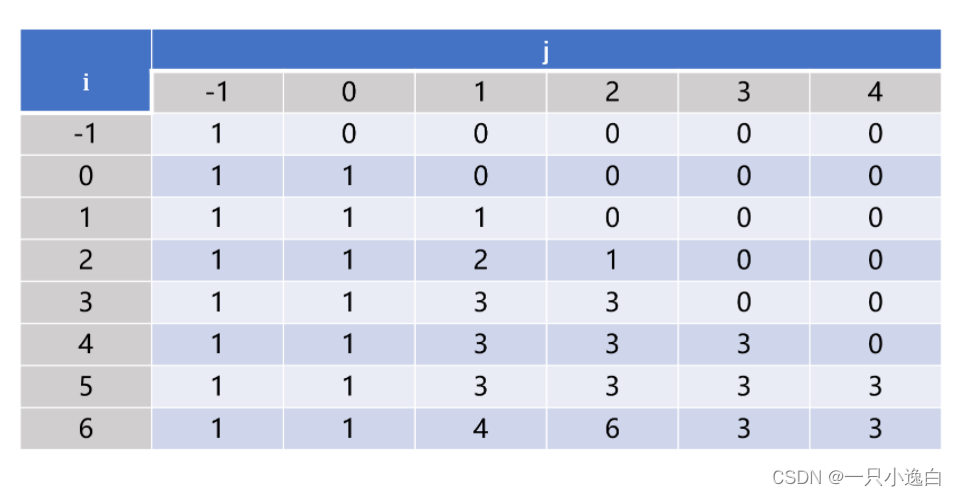
上式成立的条件都是 i >= j，另外 f(i, -1) 表示字符串 s[0] ~ s[i] 中与空字符串相等的子序列个数，所以 f(i, -1) = 1，f(i, -1) 表示空字符串中与字符串 t[0] ~ t[j] 相等的子序列个数，所以 j > 0 时 f(-1 ,j) = 0。以 s = “appplep”, t = “apple” 为例子二维 DP 矩阵如下图

时间复杂度为

O(mn)

，空间复杂度为

O(mn)

。

classSolution{public:intnumDistinct(string s, string t){if(s.size()< t.size()){return0;}

        vector<vector<unsignedint>>dp(s.size()+1, vector<unsignedint>(t.size()+1,0));
        dp[0][0]=1;for(int i =0; i < s.size();++i){
            dp[i +1][0]=1;for(int j =0; j <= i && j < t.size();++j){
                dp[i +1][j +1]=(s[i]== t[j])? dp[i][j]+ dp[i][j +1]: dp[i][j +1];}}return dp[s.size()][t.size()];}};

098. 路径的数目

题目：

一个机器人位于一个

m x n

网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？

示例：

输入：m = 3, n = 7
输出：28

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 109

思路：

用 f(i, j) 表示从 (0, 0) 到达 (m, n) 的路径数。当 i == 0 时，机器人位于格子的第一行，所以不可能从某一个位置向下走一步到达，只能从 (0, 0) 不断往右走到达，所以 f(0, j) = 1，同理可得 f(i, 0) = 1。在 i != 0 且 j != 0 时，机器人有两种办法到达 (i, j) 分别时从 (i - 1, j) 向右走一步以及从 (i, j - 1) 向下走一步，所以 f(i, j) = f(i - 1, j) + f(i, j - 1)。
时间复杂度为

O(mn)

，空间复杂度为

O(mn)

可以优化成一维数组，dp[i] = dp[i] + dp[i-1]; 但是懒得写了，前面和下一题都有优化的方法

classSolution{public:intuniquePaths(int m,int n){
        vector<vector<int>>dp(m, vector<int>(n,0));for(int i =0; i < m; i++){for(int j =0; j < n; j++){// 第一列 and 第一行 都是只有一条从原点出发的路径,初始化为1if(i ==0){
                    dp[i][j]=1;continue;}if(j ==0){
                    dp[i][j]=1;continue;}// 当前路径等于上面的路径 + 左边的路径
                dp[i][j]= dp[i-1][j]+ dp[i][j-1];}}return dp[m-1][n-1];}};

099. 最小路径之和

题目：

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：一个机器人每次只能向下或者向右移动一步。

示例：

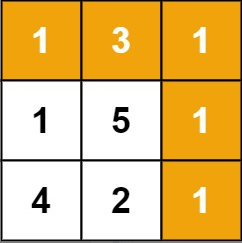
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

思路：

机器人只能向下或者向右移动一步
所以这个位置路径最小值 = 左边和上边最小值 + 本身值
状态转移方程 dp[i][j] = min(dp[i][j-1], dp[i-1][j]) + grid[i][j];
可以转化成一维数组 dp[j] = min(dp[j-1], dp[j]) + grid[i][j];

classSolution{public:intminPathSum(vector<vector<int>>& grid){int n = grid.size();int m = grid[0].size();
        vector<int>dp(m);

        dp[0]= grid[0][0];for(int i =1; i < m; i++){
            dp[i]= dp[i-1]+ grid[0][i];}for(int i =1; i < n; i++){
            dp[0]= dp[0]+ grid[i][0];for(int j =1; j < m; j++){
                dp[j]=min(dp[j-1], dp[j])+ grid[i][j];}}return dp[m-1];}};