本文描述如何扩展图神经网络(GNNs)的最简单公式,以编码知识图谱(KGs)等多关系数据的结构。
这篇文章包括4个主要部分:
- 介绍了描述KGs特性的多关系数据的核心思想;
- GNN体系结构中包含的标准组件摘要;
- gnn最简单公式的描述,称为图卷积网络(GCNs);
- 讨论如何以关系图卷积网络(R-GCN)的形式扩展GCN层,对多关系数据进行编码。
知识图作为多关系数据
基本图结构包括用于连接节点的无向,无类型和唯一边。例如,在哲学领域,我们可以定义两个由“苏格拉底”和“柏拉图”实体表示的节点之间的链接。在这种特定情况下,我们不提供关于这些哲学家之间关系的任何信息。。
另一方面,KG包括定向的,类型化的和用于连接节点的多个边。考虑我们正在运行的示例,从“苏格拉底”到“柏拉图”的连接可以用“影响”来标记。在相反的方向上,可以建立从“柏拉图”到“苏格拉底”的另一种连接,可以用“影响者”来标记。
换句话说,KG是基于图的结构,其节点表示真实世界的实体,而边沿则定义了这些实体之间的多个关系。
图神经网络
GNN的主要组件包括(I)输入层,(ii) GNN层,(iii)多层感知器(MLP)预测层。
在该体系结构中,GNN层是编码局部图结构的关键组件,用于更新节点表示。不同的GNN层使用不同类型的局部图结构聚合。为了说明使用GNN行为,我们使用NumPy进行编码,完成以下3个主要成分:
- 表示节点的独热向量(无特征)矩阵
- 描述节点隐藏特征的权值矩阵
- 定义节点间无向边的邻接矩阵
### One-hot vector representation of nodes (5,5):
X = np.eye(5, 5)
n = X.shape[0]
np.random.shuffle(X)
print(X)
-----
[[0. 0. 1. 0. 0.] # Node 1
[0. 1. 0. 0. 0.] # Node 2
[0. 0. 0. 0. 1.] ...
[1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0.]] # Node 5
### Weight matrix (5,3)
# Dimension of the hidden features
h = 3
# Random initialization with Glorot and Bengio
W = np.random.uniform(-np.sqrt(1./h), np.sqrt(1./h),(n,h))
print(W)
-----
[[-0.4294049 0.57624235 -0.3047382 ]
[-0.11941829 -0.12942953 0.19600584]
[ 0.5029172 0.3998854 -0.21561317]
[ 0.02834577 -0.06529497 -0.31225734]
[ 0.03973776 0.47800217 -0.04941563]]
### Adjacency matrix of an undirect Graph (5,5)
A = np.random.randint(2, size=(n, n))
# Include the self loop
np.fill_diagonal(A, 1)
# Symmetric adjacency matrix (undirected graph)
A_und = (A + A.T)
A_und[A_und > 1] = 1
print(A_und)
-----
[[1 1 1 0 1] # Connections to Node 1
[1 1 1 1 1]
[1 1 1 1 0]
[0 1 1 1 1]
[1 1 0 1 1]]
考虑到这些因素,通过更新过程的所谓“消息传递框架”(message passing framework ,Gilmer ,2017)执行了“递归邻域扩散”( recursive neighborhood diffusion ,Dwivedi,2020)。邻居的特征通过边缘作为消息传递给目标节点。具体地说,所需的操作如下(请参阅NumPy代码了解更多细节):
- 涉及节点和权重矩阵(包括其隐藏特征)的初始表示的线性变换(或投影)。
- 邻域扩散以更新节点的表示形式,汇总其邻居的隐藏特征。针对每个节点并行计算此操作。
### Linear transformation
L_0 = X.dot(W)
print(L_0)
-----
[[ 0.5029172 0.3998854 -0.21561317] # Node 1 (3rd row of W)
[-0.11941829 -0.12942953 0.19600584] # Node 2 (2nd row of W)
[ 0.03973776 0.47800217 -0.04941563] # Node 3 (5th row of W)
[-0.4294049 0.57624235 -0.3047382 ]
[ 0.02834577 -0.06529497 -0.31225734]] # Node 5 (4th row of W)
### GNN - Neighborhood diffusionND_GNN = A_und.dot(L_0)
print(ND_GNN)
-----
[[ 0.45158244 0.68316307 -0.3812803 ] # Updated Node 1
[ 0.02217754 1.25940542 -0.6860185 ]
[-0.00616823 1.3247004 -0.37376116]
[-0.48073966 0.85952002 -0.47040533]
[-0.01756022 0.78140325 -0.63660287]]
### Test on the aggregation
assert(ND_GNN[0,0] == L_0[0,0] + L_0[1,0] + L_0[2,0] + L_0[4,0])
观察邻域扩散的结果,您可以注意到节点1的更新表示
[0.5029172 0.3998854 -0.21561317] # Node 1
为表示节点1 (self-loop)、节点2、节点3、节点4的向量之和。这些节点根据前面定义的邻接矩阵连接到节点1。
[ 0.5029172 0.3998854 -0.21561317] # Node 1
[-0.11941829 -0.12942953 0.19600584] # Node 2
[ 0.03973776 0.47800217 -0.04941563] # Node 3
[ 0.02834577 -0.06529497 -0.31225734] # Node 5
本节中描述的代码可以在数学上形式化如下:
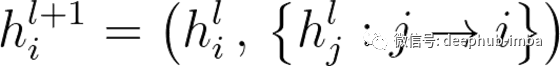
通用更新功能(h_i ^(l + 1)),用于将邻居(h_j ^ l)的隐藏特征聚合到中心节点(h_i ^ l)的隐藏特征
图卷积网络(GCNs)
在被称为普通图卷积网络(GCNs)的GNNs的公式中,节点更新是通过“对邻域特征进行各向同性平均运算”来执行的(isotropic averaging operation over the neighborhood features ,Dwivedi,2020)。换句话说,相邻节点同样有助于更新中心节点的表示。更准确地说,在普通GCNs(Vanilla GCNs)的具体情况下,执行了各向同性平均计算。这个计算需要一个由每个节点的度表示的新元素,该度由其连接边的数量组成。
### Degree vector (degree for each node)
D = A_und.sum(axis=1)
print(D)
-----
[4 5 4 4 4] # Degree of Node 1
### Reciprocal of the degree (diagonal matrix)
D_rec = np.diag(np.reciprocal(D.astype(np.float32)))
print(D_rec)
-----
[[0.25 0. 0. 0. 0. ] # Reciprocal value of Node 1 degree
[0. 0.2 0. 0. 0. ]
[0. 0. 0.25 0. 0. ]
[0. 0. 0. 0.25 0. ]
[0. 0. 0. 0. 0.25]]
### GCN - Isotropic average computation
ND_GCN = D_rec.dot(ND_GNN)
print(ND_GCN)
-----
[[ 0.11289561 0.17079077 -0.09532007] # Updated Node 1 (with deg)
[ 0.00443551 0.25188109 -0.1372037 ]
[-0.00154206 0.3311751 -0.09344029]
[-0.12018491 0.21488001 -0.11760133]
[-0.00439005 0.19535081 -0.15915072]]
### Test on the isotropic average computation:
assert(ND_GCN[0,0] == ND_GNN[0,0] * D_rec[0,0])
度向量的每个元素代表i节点的度值。实际上,向量的第一个元素等于4,因为邻接矩阵显示4个节点连接到节点1。然后计算度数的倒数,以实现连接到节点的边的平均贡献。最后,根据GCN公式进行各向同性平均计算。使用节点1度执行平均计算的节点1的更新表示等于:
[ 0.11289561 0.17079077 -0.09532007]
通过将以下向量(表示节点1的聚合表示)乘以其度数的倒数(0.25),可以得到此向量:
[ 0.45158244 0.68316307 -0.3812803 ]
本节中描述的代码可以通过数学形式化如下:
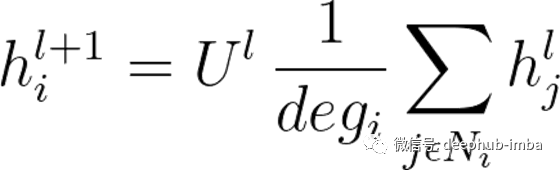
描述GCN层执行的各向同性平均聚合的函数。U是投影步长的结果,deg是中心节点的度数。N是其邻居数
关系图卷积网络(Relational-GCN)
前面的示例描述了GCN在无向和无类型图上的行为。如前所述,更新过程基于以下步骤(在以下说明中,为简单起见,不考虑节点度)。
通过将(i)单热点特征矩阵与(ii)权重矩阵相乘,可以实现投影步骤(或线性变换)。
(i)2D矩阵(n,n),用于定义表示节点的独热向量。
(ii)定义隐藏特征的2D矩阵(n,h)。当前矩阵仅编码一种类型的关系。
将邻接矩阵(i)与投影步骤产生的矩阵(ii)相乘,即可实现一个聚合步骤。
(i)2D对称矩阵(n,n),描述无向和无类型的边。
(ii)投影步骤产生的2D矩阵(n,h)。
为了扩展GCN层以编码KG结构,我们需要将我们的数据表示为有向图和多类型图。更新/聚合过程与上一个类似,但是组成部分稍微复杂一些。下面提供了有关执行步骤的详细信息。
通过将(i)独热点特征矩阵与(ii)权重张量相乘,可以实现投影步骤。
(i)定义节点初始特征的2D矩阵(n,n)。
(ii)描述节点隐藏特征的3D张量(r,n,h)。该张量能够通过堆叠大小为(n,h)的r批矩阵来编码不同的关系。每个批都编码单个类型的关系。
投影步骤将不再是矩阵的简单乘法,而是批次矩阵乘法,其中(i)与(ii)的每一批相乘。
聚合步骤,是通过将(i)(有向)邻接张量乘以(ii)由投影步骤得出的张量而实现的。
(i)描述有向和r型边的3D张量(r,n,n)。该张量由r批邻接矩阵(n,n)组成。每个邻接矩阵根据特定类型的关系描述节点之间的边。而且,与无向图的邻接矩阵相比,这些邻接矩阵中的每一个都不对称,因为它编码特定的边缘方向。
(ii)由上述投影步骤产生的3D张量(r,n,h)。
就像投影步骤一样,聚合阶段包括一个批处理矩阵乘法。每批(i)乘以每批(ii)。此汇总定义了每个批次的GCN转换。在该过程的最后,必须将批次加在一起(R-GCN),以获得根据不同关系类型并入邻域聚合的节点表示。
以下代码示例显示了R-GCN层的行为,该行为编码具有两种类型的边(或关系)的有向和多类型图或KG。
### Recall: One-hot vector representation of nodes (n,n)
print(X)-----
[[0. 0. 1. 0. 0.] # Node 1
[0. 1. 0. 0. 0.] ...
[0. 0. 0. 0. 1.]
[1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0.]]
### Number of relation types (r)
num_rels = 2
### Weight matrix of relation number 1 (n,n)
## Initialization according to Glorot and Bengio (2010))
W_rel1 = np.random.uniform(-np.sqrt(1./h),np.sqrt(1./h),(n,h))
print(W_rel1)
-----
[[-0.46378913 -0.09109707 0.52872529]
[ 0.03829597 0.22156061 -0.2130242 ]
[ 0.21535272 0.38639244 -0.55623279]
[ 0.28884178 0.56448816 0.28655701]
[-0.25352144 0.334031 -0.45815514]]
### Weight matrix of relation number 2 (n,h)
## Random initialization with uniform distribution
W_rel2 = np.random.uniform(1/100, 0.5, (n,h))
print(W_rel2)
-----
[[0.22946783 0.4552118 0.15387093]
[0.15100992 0.073714 0.01948981]
[0.34262941 0.11369778 0.14011786]
[0.25087085 0.03614765 0.29131763]
[0.081897 0.29875971 0.3528816 ]]
### Tensor including both weight matrices (r,n,h)
W_rels = np.concatenate((W_rel1, W_rel2))
W_rels = np.reshape(W_rels,(num_rels, n, h))
print(W_rels)
-----
[[[-0.46378913 -0.09109707 0.52872529]
[ 0.03829597 0.22156061 -0.2130242 ]
[ 0.21535272 0.38639244 -0.55623279]
[ 0.28884178 0.56448816 0.28655701]
[-0.25352144 0.334031 -0.45815514]]
[[ 0.22946783 0.4552118 0.15387093]
[ 0.15100992 0.073714 0.01948981]
[ 0.34262941 0.11369778 0.14011786]
[ 0.25087085 0.03614765 0.29131763]
[ 0.081897 0.29875971 0.3528816 ]]]
### Linear trasformationwith batch matrix multiplication (r,n,h)
L_0_rels = np.matmul(X, W_rels)
print(L_0_rels)
-----
[[[ 0.21535272 0.38639244 -0.55623279] # Node 1 (3rd row of W_rel1)
[ 0.03829597 0.22156061 -0.2130242 ]
[-0.25352144 0.334031 -0.45815514]
[-0.46378913 -0.09109707 0.52872529]
[ 0.28884178 0.56448816 0.28655701]]
[[ 0.34262941 0.11369778 0.14011786] # Node 1 (3rd row of W_rel2)
[ 0.15100992 0.073714 0.01948981]
[ 0.081897 0.29875971 0.3528816 ]
[ 0.22946783 0.4552118 0.15387093]
[ 0.25087085 0.03614765 0.29131763]]]
### Adjacency matrix of relation number 1 (n,n)
A_rel1 = np.random.randint(2, size=(n, n))
np.fill_diagonal(A, 0) # No self_loop
print(A_rel1)
-----
[[0 1 1 1 1] # Connections to Node 1 with Rel 1
[1 1 0 0 1] # Connections to Node 2 with Rel 1
[1 0 0 1 0]
[0 0 1 1 1]
[1 1 0 1 0]]
### Adjacency matrix of relation number 2 (n,n)
A_rel2 = np.random.randint(3,size=(n,n))
np.fill_diagonal(A_rel2, 0) # No self loop
A_rel2[A_rel2>1] = 0
-----
[[0 0 0 1 0] # Connections to Node 1 with Rel 2
[1 0 0 0 0] # Connections to Node 2 with Rel 2
[1 0 0 1 1]
[0 0 0 0 0]
[0 1 0 0 0]]
### Tensor including both adjacency matrices (r,n,n)
A_rels = np.concatenate((A_rel1, A_rel2))
A_rels = np.reshape(A_rels, (num_rels, n, n))
print(A_rels)
-----
[[[0 1 1 1 1] # Connections to Node 1 with Rel 1
[1 1 0 0 1]
[1 0 0 1 0]
[0 0 1 1 1]
[1 1 0 1 0]]
[[0 0 0 1 0] # Connections to Node 2 with Rel 2
[1 0 0 0 0]
[1 0 0 1 1]
[0 0 0 0 0]
[0 1 0 0 0]]]
### (GCN) Neighborhood diffusion for each typed edge (r,n,h)
ND_GCN = np.matmul(A_rels, L_0_rels)
print(ND_GCN)
-----
[[[-0.39017282 1.0289827 0.14410296] # Updated Node 1 with Rel 1
[ 0.54249047 1.17244121 -0.48269997]
[-0.24843641 0.29529538 -0.0275075 ]
[-0.42846879 0.80742209 0.35712716]
[-0.21014043 0.51685598 -0.2405317 ]]
[[ 0.22946783 0.4552118 0.15387093] # Updated Node 1 with Rel 2
[ 0.34262941 0.11369778 0.14011786]
[ 0.82296809 0.60505722 0.58530642]
[ 0. 0. 0. ]
[ 0.15100992 0.073714 0.01948981]]]
### (R-GCN) Aggregation of GCN (n,h)
RGCN = np.sum(ND_GCN, axis=0)
print(RGCN)
-----
[[-0.16070499 1.48419449 0.29797389] Updated Node 1(Rel 1 + Rel 2)
[ 0.88511988 1.28613899 -0.34258211]
[ 0.57453168 0.9003526 0.55779892]
[-0.42846879 0.80742209 0.35712716]
[-0.05913052 0.59056998 -0.22104189]]
### Test of the aggregation
assert(RGCN[0,0] == L_0_rels[0,1,0] + L_0_rels[0,2,0] + L_0_rels[0,3,0] + L_0_rels[0,4,0] + L_0_rels[1,3,0])
你可以从这个例子中注意到,邻域扩散(GCN)的结果是一个大小为(r, n,h)的3D张量,而不是一个大小为(n,h)的2D矩阵。原因是,对于每种类型的关系,邻居扩散都是以一种单独的方式进行的。R-GCN层对GCN所实现的每种关系类型的节点表示进行聚合。为了阐明这个方面,考虑节点1的聚合表示
[-0.16070499 1.48419449 0.29797389]
这个向量是由节点1的更新表示与关系1相加得到的
[-0.39017282 1.0289827 0.14410296]
与关系2的节点1的更新表示
[ 0.22946783 0.4552118 0.15387093]
本节中描述的代码可以在数学上形式化如下:

描述R-GCN层执行的各向同性聚合的功能。与先前的功能相比,此聚合包括进一步的求和运算,该运算包括节点i和j之间的不同类型的边缘(E_ij)。为了简单起见,省略了节点的度数
总结
R-GCN代表了强大的图神经体系结构,可对诸如KG之类的多关系数据进行编码。在以后的文章中,我将向您展示如何利用这种编码能力在KG中执行特定任务,包括节点分类和链接预测。
如果要直接运行和测试代码,可以在此处下载可用的笔记本:
https://github.com/giuseppefutia/notebooks/blob/main/rgcn.ipynb
以下研究论文提供了有关R-GCN架构的更多详细信息:
https://arxiv.org/abs/1703.06103
作者:Giuseppe Futia
原文地址:https://towardsdatascience.com/graph-neural-networks-for-multi-relational-data-27968a2ed143
deephub翻译组