softmax 函数在机器学习中无处不在:当远离分类边界时,它假设似然函数有一个修正的指数尾。
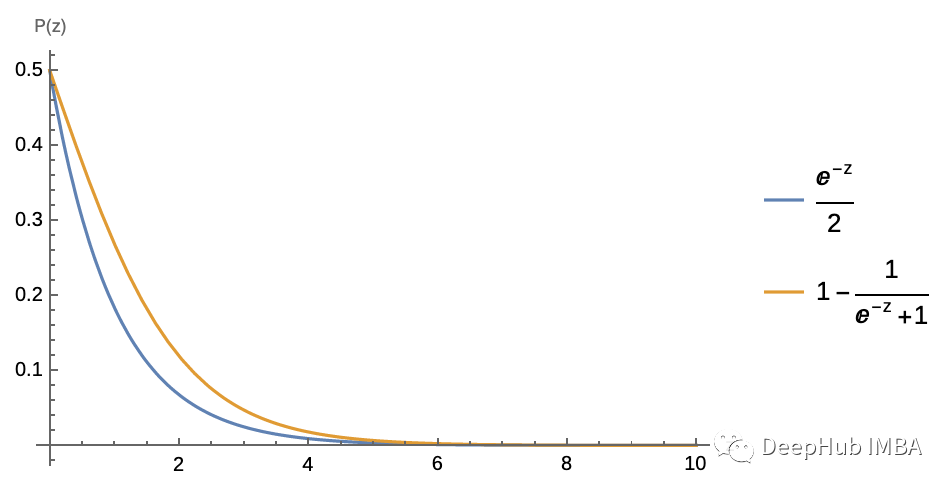
但是新数据可能不适合训练数据中使用的 z 值范围。如果出现新的数据点softmax将根据指数拟合确定其错误分类的概率;错误分类的机会并不能保证遵循其训练范围之外的指数(不仅如此——如果模型不够好,它只能将指数拟合到一个根本不是指数的函数中)。为避免这种情况将 softmax 函数包装在一个范围限制的线性函数中(将其概率限制在 1/n 和 1-1/n 之内)可能会有所帮助,其中 n 是训练数据中的样本数:
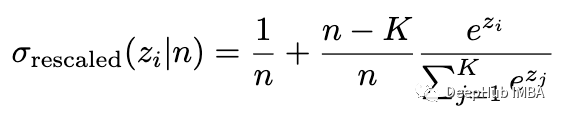
但是我们将通常的 softmax 函数视为最佳拟合曲线而不是似然函数,并根据(离散)高斯统计(首先用于两类)计算其误差:
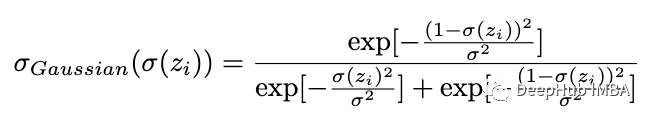
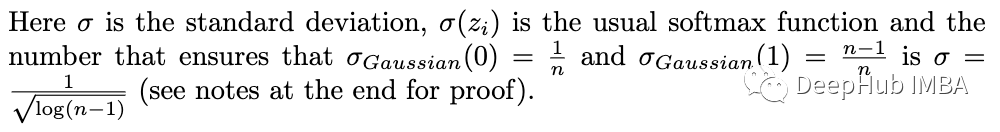
简化这个表达式后,我们得到:
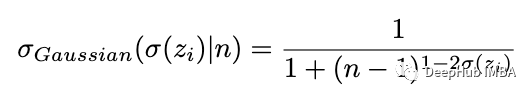
我们绘制原始函数以及 n=50,500,10000,1000000 的新高斯 softmax 函数:
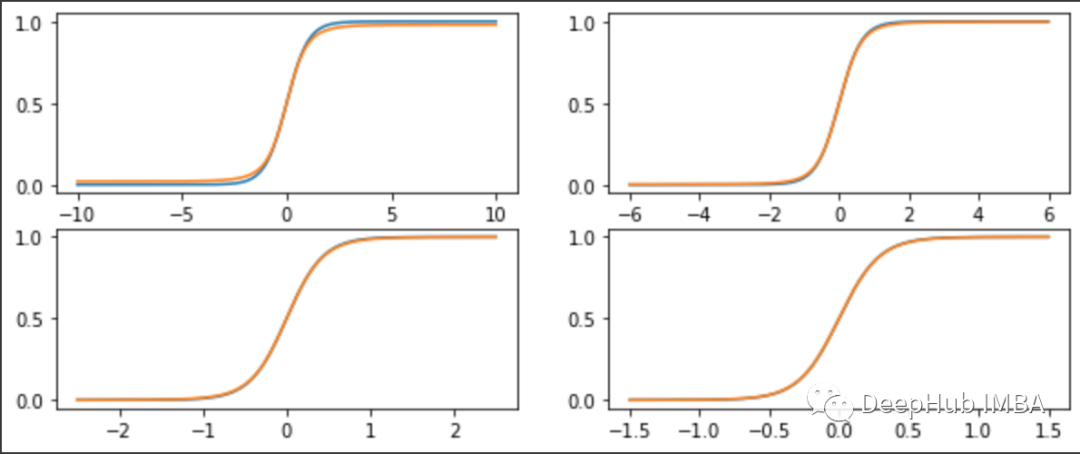
我们看到,该函数仅在 n<500 左右时出现不同(它是 log(n-1)/2)。其实并不是这样,我们绘制 n = 100 万的函数的对数:
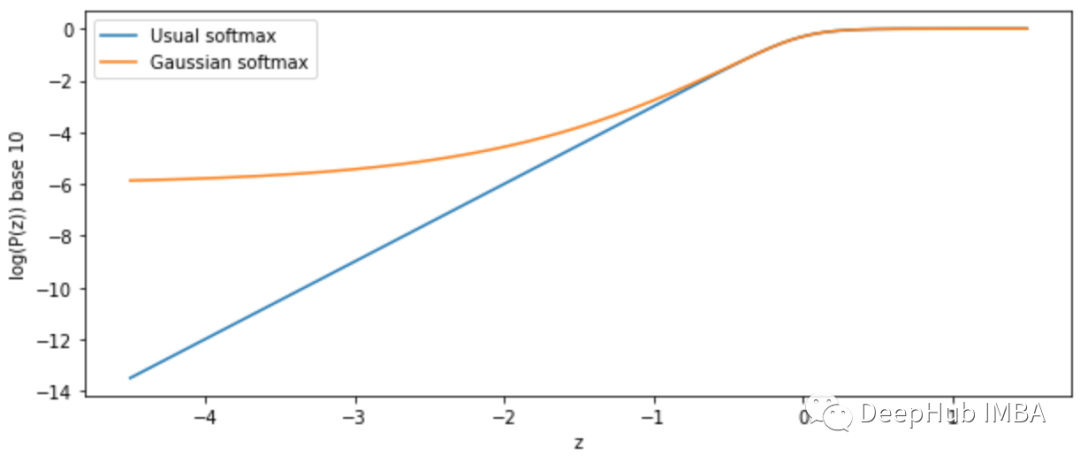
虽然通常的 softmax 函数的概率是无界的,并且很快就用100万个数据点实现了1 / 10¹²的准确性,新的高斯 softmax 函数基于样本数量稳定在超过 10⁶ 的水平。
将初始线性缩放softmax函数与n = 100万的高斯softmax函数进行比较(我们查看对数图,因为它们在线性图上看起来是一样的):
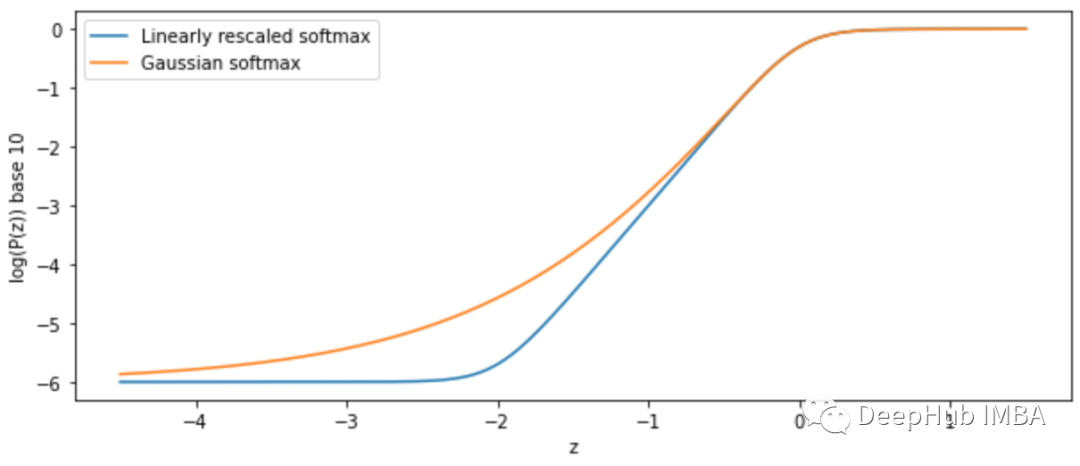
可以看到虽然两者都接近10分之1的极限、但它们的同质率却非常不同,线性逼近达到最高精度的速度大约是高斯softmax函数的两倍。
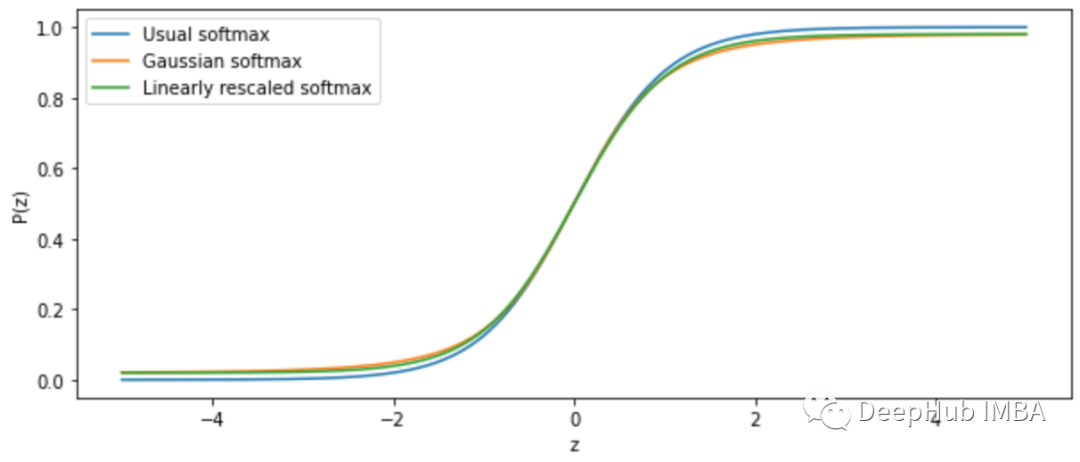
最后,我们绘制n = 50的所有三个函数:
由于链式法则,新高斯softmax函数的导数计算并不比原softmax函数的导数更难:

贝叶斯和Evidential Neural Networks 被用于计算使用深度学习做出的预测的实际概率。但是在许多情况下,softmax函数的输出仍然被用作预测准确的概率。本文提出了一种基于最小误差界和高斯统计量的softmax函数的安全快速扩展,可以在某些情况下作为softmax的替代
如何将其扩展到两个以上的类?
扩展到两个以上的类在数学上很简单,只需将 1-sigma 的高斯替换为单个 sigma 上高斯的总和。以 n-1 作为基数,找到 1/n 的下限和 (n-1)/n 的上限,并且可以通过对所有中间 sigma 求和以封闭形式计算导数。但是以下这种情况:有11 个类,一个(称为 A)的 sigma 为 0,其他的 sigma 为 0.1,我们可能认为它是 1/n,使用通常的 softmax会返回 A 的概率为0,而高斯softmax返回1/(10*n^(1/10))。因为我们不知道它到底是什么(各个分类概率很”平均“),因为n < 100 万时返回约为 0.04,其他类为 0.095(因为N对值不太敏感),这意味着基于真正看到的内容的不确定性,存在明显的溢出效应。
所以高斯 softmax 的不适合有许多彼此非常接近的类别(例如猫的品种)和彼此相距很远的类别(例如猫与船等)混合的数据。但是对一些可以将“我不确定”进行后处理的情况高斯 softmax 还是可以使用的,比如推荐用户进一步收集数据等。
作者:Alex Roberts