【深度学习】6-卷积过程中数据的结构变化

🚩 前言

在学习卷积神经网络时，我对于卷积过程中数据的结构变化常感困惑不解（如改变数组的维度顺序），因此在这里做一些整理。

文章目录

多通道特征图

1. 多通道的形成

通过对一张图片应用一个滤波器（卷积核）进行卷积运算，我们将得到单通道的特征图。那么通过对一张图片应用多个滤波器，就可以得到多通道的特征图。

图片来自《深度学习入门：基于python的理论与实现》

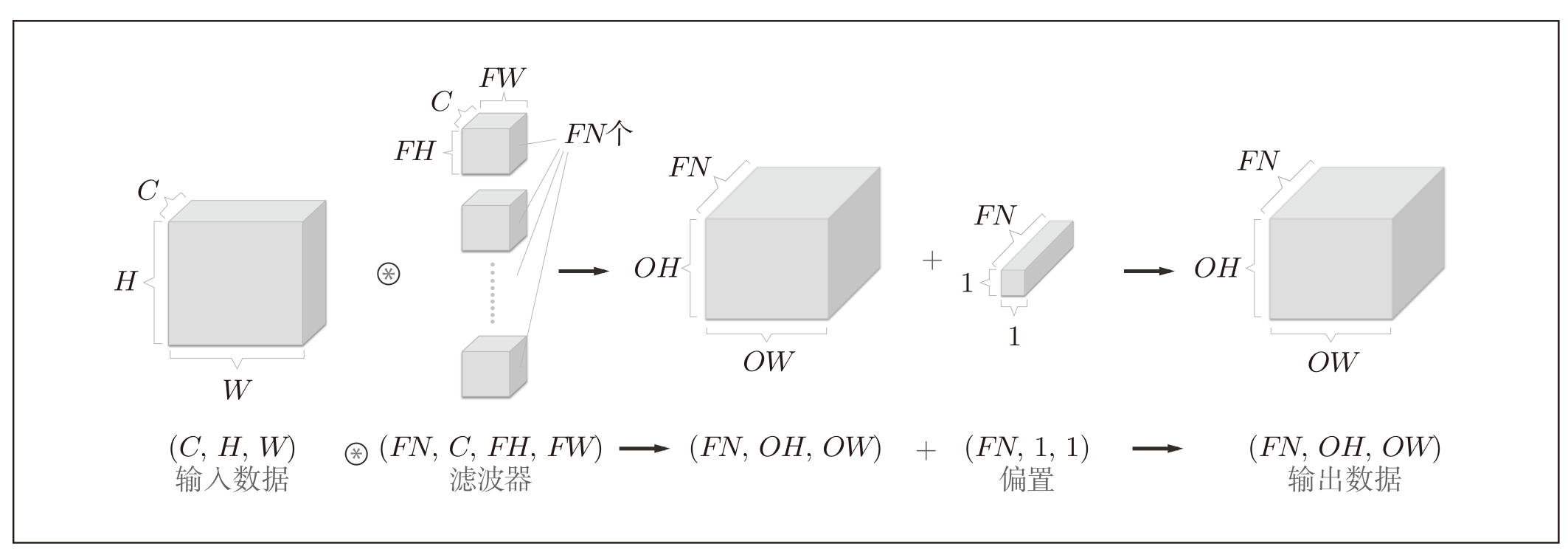
因此，虽然我们作为输入数据的图片也有通道数，输出的特征图也有通道数，但它们其实在卷积过程中并不具有因果关系。输出特征图的通道数仅由所应用的滤波器的数量决定，而滤波器的数量是人为设定的超参数。

即使输入的图片仅仅是单通道的二维数据，通过应用多个滤波器的卷积，同样可以得到多通道的特征图。特征图的不同通道之间，你可以把它们想象成核磁共振和CT之间的关系（这个比喻可能不是很恰当）。

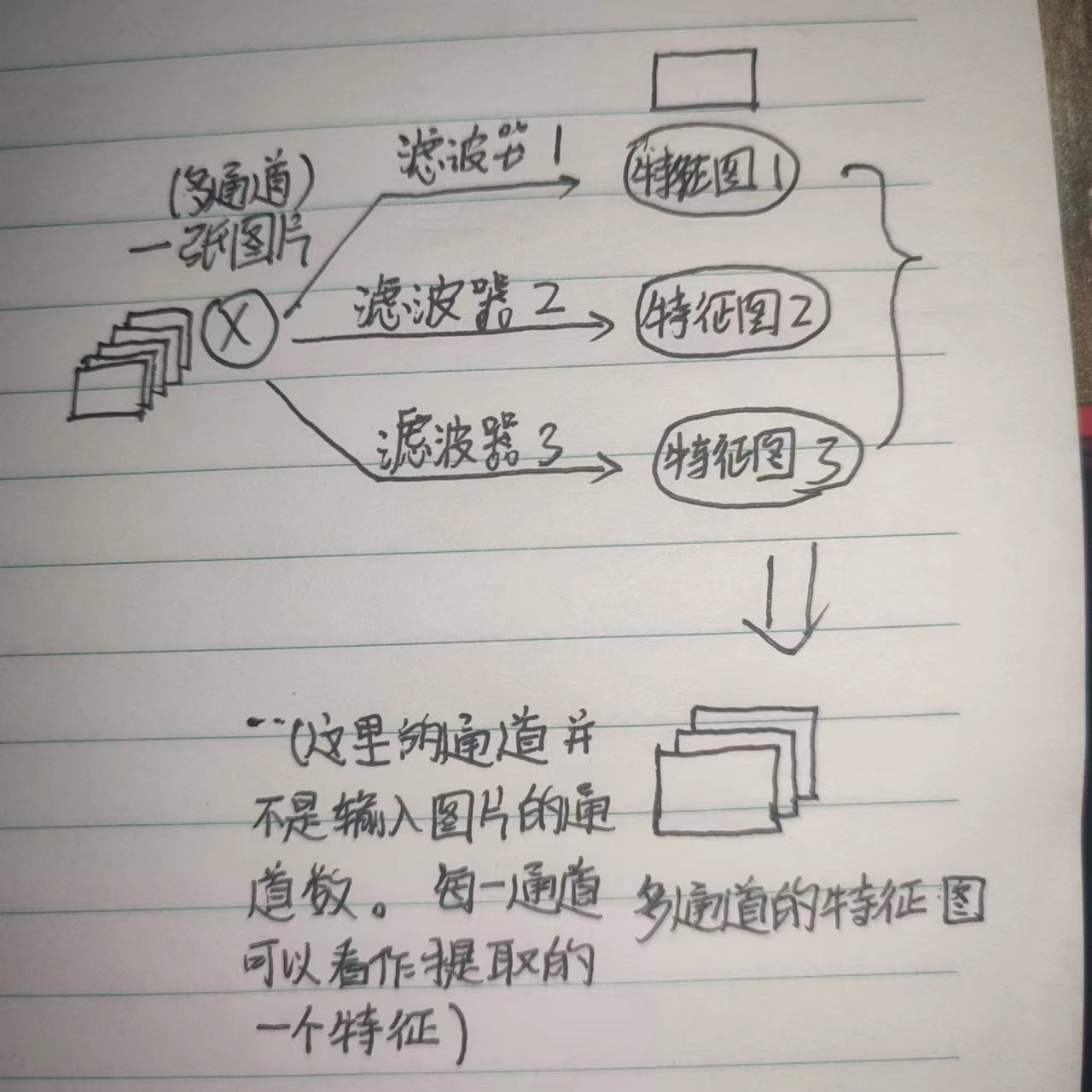
2. 相比普通的全连接层

在运用了多个滤波器时，我们会发现卷积网络层和之前多分类问题的结构很相似。实际上，有时一个滤波器就被称作一个权值。

我们可以把卷积过程的一个滤波器的输出来和多分类中的一个输出y对比，发现它们都是利用到了所有的输入数据，然后得到一个输出。不同的是，多分类问题中每个输出只是那些所有输入数据的加权和；而卷积得到的一个输出是一个矩阵（代表一个通道），矩阵的每一个元素都是局部相邻的输入数据的加权和。

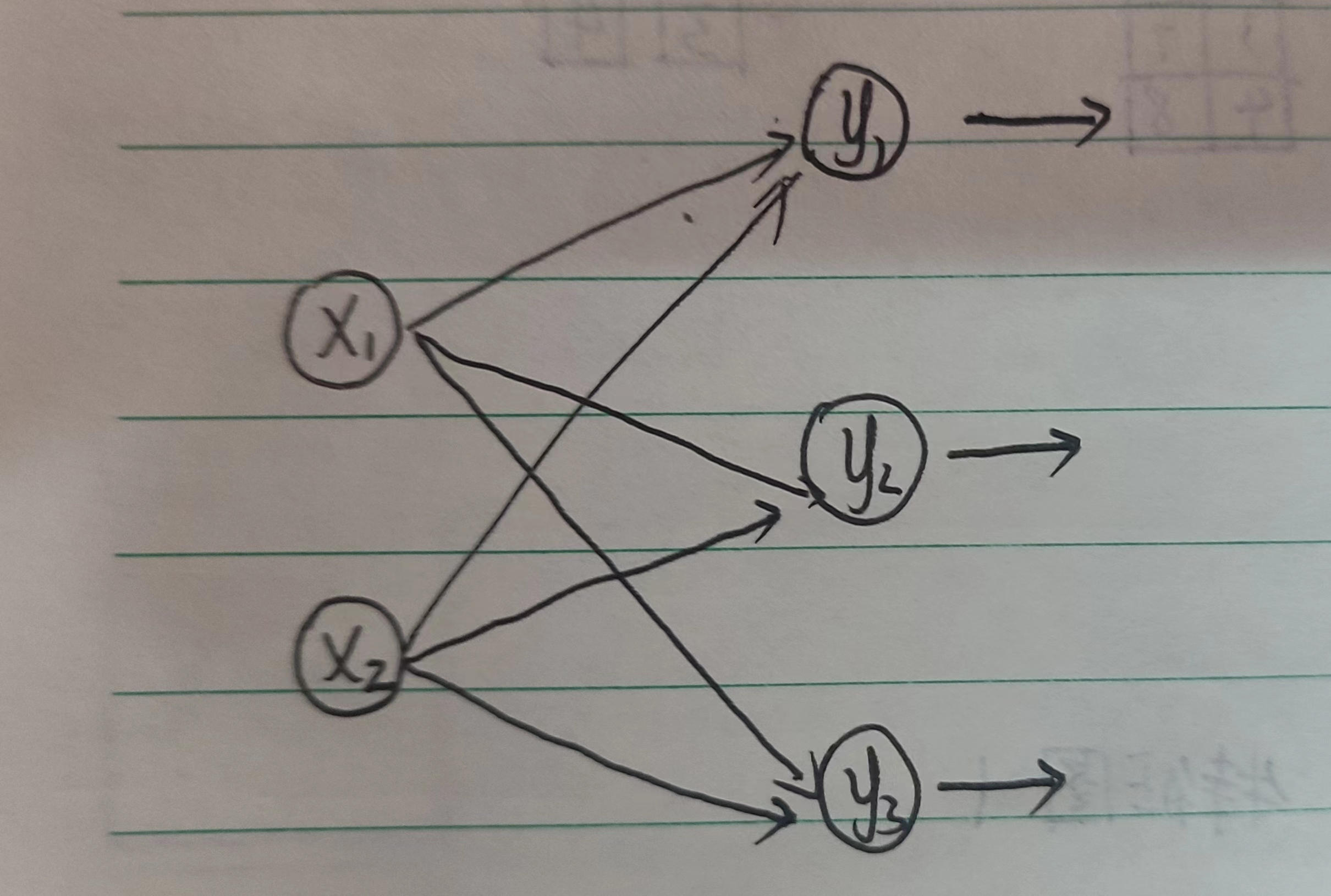
大量局部信息的保留对于图像的识别很有帮助，可以参考长文解析Resnet50的算法原理，这篇文章使用的是比较通俗易懂的写法。

卷积批处理中数据的结构

1. 卷积层的实现代码

# 用im2col来实现卷积层classConvolution:def__init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad
        
    defforward(self, x):
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        out_h =int(1+(H +2* self.pad - FH)/ self.stride)
        out_w =int(1+(W +2* self.pad - FW)/ self.stride)# 输入数据横向展开，滤波器纵向展开
        col = im2col(x, FH, FW, self.stride, self.pad)
        col_W = self.W.reshape(FN,-1).T
        out = np.dot(col, col_W)+ self.b
        
        out = out.reshape(N, out_h, out_w,-1).transpose(0,3,1,2)return out

2. 数据的结构分析

书上通常用不同的字母以及它们的顺序，来描述多维数据的结构。例如

    (
   
   
    C
   
   
    ,
   
   
    H
   
   
    ,
   
   
    W
   
   
    )
   
  
  
   (C,H,W)
  
 
(C,H,W)，其中C表示通道数，H表示高，W表示宽。但有时仍感到有些晦涩，特别是当这些维度发生交换的时候，例如代码中的

out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

一句，为什么输出应该

reshape

为

    (
   
   
    N
   
   
    ,
   
   
    H
   
   
    ,
   
   
    W
   
   
    ,
   
   
    C
   
   
    )
   
  
  
   (N,H,W,C)
  
 
(N,H,W,C)的形式？

这时，我们就需要一个例子来帮助我们理解它具体的过程。下面是处理一张单通道图片的例子。（前面说了输出数据的通道数只与滤波器的数量有关，因此我们这里的输入数据是单通道还是多通道其实关系不大）

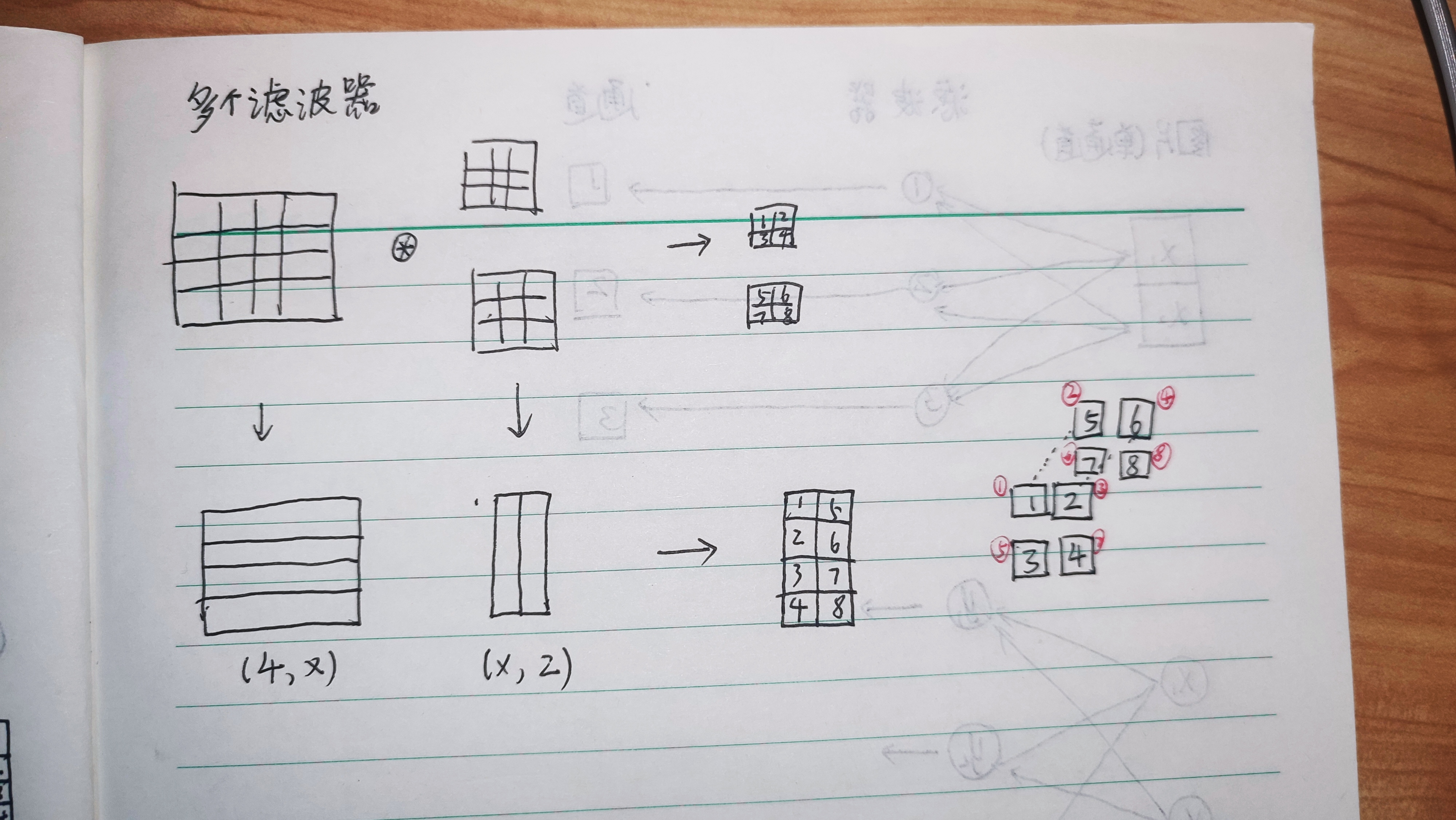
图中，上面是没有进行

    i
   
   
    m
   
   
    2
   
   
    c
   
   
    o
   
   
    l
   
  
  
   im2col
  
 
im2col展开的卷积过程（方便直观理解），下面是进行了展开的过程（方便在计算机上实现）

• reshape虽然可以改变数组的形状，但其实是受限于原来数据元素的顺序的，而只是重新进行了一次划分来改变维度。例如， [ 1 , 2 , 3 , 4 ] [1,2,3,4] [1,2,3,4]可以被重新划分为 [ [ 1 , 2 ] , [ 3 , 4 ] ] [ [1,2],[3,4] ] [[1,2],[3,4]]而变成二维数组，但却不能被重新划分为 [ [ 1 , 3 ] , [ 2 , 4 ] ] [ [1,3],[2,4] ] [[1,3],[2,4]]（从这样的表示法来看，就是你只能改变括号，而不能改变数字的顺序）

于是在规则下，就催生了我们上面的过程来实现我们的目标。

感谢阅读