网安技术与应用(6)——基于Paillier的安全计算

文章目录

代码见
基于Paillier的安全计算代码

一、实验概述

1、实验原理

1.1 Paillier原理

1.2 开源包半同态加密phe

半同态加密（Partially Homomorphic Encryption, PHE）：只支持加法或乘法中的一种运算。其中，只支持加法运算的又叫加法同态加密（Additive Homomorphic Encryption, AHE）。该开源包支持加法同态。满足

• E(a)+E(b)=E(a+b)
• E(a)×b=E(ab)

2、实验内容

（1）阅读文献[1]，理解加性同态加密算法Paillier的基本原理；

（2）实现Paillier同态加密算法；

• 支持数据加密和解密操作
• 能根据安全性要求选择合适参数

（3）采用Socket编程（或其它方式）建立两个计算方的通信连接；

（4）实现文献[2,3]中的SM、SSED、SBD和SMIN算法并验证正确性；

（5）扩展：基于所实现的基本运算模块，实现一个自定义计算任务， 如计算汉明距离、编辑距离等。

• 计算任务具有一定复杂性
• 验证算法正确性

[1] Paillier P. Public-key cryptosystems based on composite degree residuosity classes[C]//International conference on the theory and applications of cryptographic techniques. Springer, Berlin, Heidelberg, 1999: 223-238.

[2] Elmehdwi Y, Samanthula B K, Jiang W. Secure k-nearest neighbor query over encrypted data in outsourced environments[C]//2014 IEEE 30th International Conference on Data Engineering. IEEE, 2014: 664-675.

[3] Samanthula B K K, Chun H, Jiang W. An efficient and probabilistic secure bit-decomposition[C]//Proceedings of the 8th ACM SIGSAC symposium on Information, computer and communications security. 2013: 541-546.

二、实验过程

1、实现并验证Paillier同态加密算法

1.1 安装phe模块

pip install phe

1.2 数据加密和解密

本步骤需要导入phe工具，查看默认的私钥大小，生成公私钥并进行数据加密和解密操作，此处涉及到2个自定义函数

• 加密函数：记录加密时间，并利用公钥对数据进行加密后输出加密数据

defEncoder(key, info):
    st = time.time()
    en_info =[key.encrypt(m)for m in info]
    ed = time.time()print("加密后数据：\n", en_info)print("加密耗时s：", ed-st)return en_info

• 解密函数：记录解密时间，并利用私钥对数据解密后输出原始数据

defDecoder(key, en_info):
    st = time.time()
    de_info =[key.decrypt(c)for c in en_info]
    ed = time.time()print("解密耗时s：", ed-st)print("原始数据:", de_info)return de_info

from phe import paillier 
# 查看密钥大小print("默认私钥大小：", paillier.DEFAULT_KEYSIZE)# 3072# 生成公私钥
pub_key, private_key = paillier.generate_paillier_keypair()# 待加密的数据
info =[210,230,11]
en_info = Encoder(pub_key, info)# 加密
de_info = Decoder(private_key, en_info)# 解密

1.3 同态测试

本步骤进行同态测试。

首先，将加密后的密文加上某个明文数字后，对新的内容进行解密，发现结果与明文相加内容相符。

其次，验证E(a)+E(b)是否等于E(a+b)，输出判断结果。

最后，验证E(a)×b是否等于E(ab)，输出判断结果。

• 同态测试函数

defHomomorphic(info, en_info, pub_key, private_key):print("\n同态测试：")
    m =3# 明文
    a, b = en_info[0:2]# a,b,c分别为对应密文
    a_sum = a + m  # 密文加明文
    a_sub = a - m  # 密文减明文
    b_mul = b * m  # 密文乘明文
    b_div = b / m  # 密文除明文# 输出密文的纯文本# print("a:",a.ciphertext()) # 密文a的纯文本形式# print("a_sum：",a_sum.ciphertext()) # 密文a_sum的纯文本形式print("a+"+str(m)+" =", private_key.decrypt(a_sum))print("a-"+str(m)+" =", private_key.decrypt(a_sub))print("b*"+str(m)+" =", private_key.decrypt(b_mul))print("b/"+str(m)+" =", private_key.decrypt(b_div))# 同态加法
    flag =(private_key.decrypt(a)+private_key.decrypt(b))== private_key.decrypt(a+b)print("E(a)+E(b)==E(a+b)?", flag)# 同态乘法
    flag = private_key.decrypt(a)*m == private_key.decrypt(m*a)print("E(a)*"+str(m)+"==E(am)?", flag)

• 主函数

# 测试加法和乘法同态
Homomorphic(info, en_info, pub_key, private_key)

2、实现并验证双方通信——Socket编程

参考链接：socket编程python实现

Python 的 socket 工具包可以实现服务器和客户端的通信，分别是通过以下几个步骤：

（1）P1(服务器端)

1. 创建套接字，绑定套接字到本地IP与端口：socket.socket(socket.AF_INET,socket.SOCK_STREAM) , s.bind()
2. 开始监听连接：s.listen()
3. 进入循环，不断接受客户端的连接请求：s.accept()
4. 接收传来的数据，或者发送数据给对方：s.recv() , s.sendall()
5. 传输完毕后，关闭套接字：s.close()

import socket

ip_port =('127.0.0.1',9999)
sk = socket.socket()# 创建套接字
sk.bind(ip_port)# 绑定服务地址
sk.listen(5)# 监听连接请求print('启动socket服务，等待客户端连接...')
conn, address = sk.accept()# 等待连接，此处自动阻塞
client_data = conn.recv(1024).decode()# 等待客户端发来的信息
conn.sendall('服务器已经收到你的信息'.encode())# 回馈信息给客户端print("收到来自客户端的信息：", client_data)
sk.close()# 关闭连接

（2）P2(客户端)

1. 创建套接字，连接服务器地址：socket.socket(socket.AF_INET,socket.SOCK_STREAM) , s.connect()
2. 连接后发送数据和接收数据：s.sendall(), s.recv()
3. 传输完毕后，关闭套接字：s.close()

import socket

ip_port =('127.0.0.1',9999)
s = socket.socket()# 创建套接字
s.connect(ip_port)# 连接服务器
inp =input("输入要发送的信息： ").strip()
s.sendall(inp.encode())print("已向服务器发送信息：", inp)
server_reply = s.recv(1024).decode()# 接收来自
s.close()# 关闭连接

3、实现并验证 SM 算法

3.1 SM目标和公式

在SM算法中，P1（Server）拥有公钥、E(a)和E(b)，P2（Client）拥有私钥

• 算法目标：P1 想要计算E(a*b)

• 算法公式：

     a
    
    
     ×
    
    
     b
    
    
     =
    
    
     
      (
     
     
      a
     
     
      +
     
     
      
       r
      
      
       a
      
     
     
      )
     
    
    
     ×
    
    
     
      (
     
     
      b
     
     
      +
     
     
      
       r
      
      
       b
      
     
     
      )
     
    
    
     −
    
    
     a
    
    
     ×
    
    
     
      r
     
     
      b
     
    
    
     −
    
    
     b
    
    
     ×
    
    
     
      r
     
     
      a
     
    
    
     −
    
    
     
      r
     
     
      a
     
    
    
     ×
    
    
     
      r
     
     
      b
     
    
   
   
     a \times b=\left(a+r_{a}\right) \times\left(b+r_{b}\right)-a \times r_{b}-b \times r_{a}-r_{a} \times r_{b} 
   
  

  a×b=(a+ra​)×(b+rb​)−a×rb​−b×ra​−ra​×rb​

• 算法过程

3.2 计算过程

• P1

1. 获得客户端发来的公钥、E(a)和E(b)
2. 计算E(a)+E(ra)=E(a+ra)、E(a)×ra=E(a×ra)、E(ra)×rb=E(ra×rb)，将E(a+ra)、E(b+rb)传送给客户端
3. 获取客户端传来的E[(a+ra)×(b+rb)]
4. 计算E(a×b)=E[(a+ra)×(b+rb)-a×ra-b×rb-ra×rb]，传给客户端

• P2

1. 向服务器发送公钥、E(a)和E(b)
2. 解密得 a+ra、b+rb
3. 向服务器发送E[(a+ra)×(b+rb)]
4. 收到来自服务器的E(a×b)

• P1代码

defSM():# 获取来自客户端的数据
    Ea, Eb = pickle.loads(conn.recv(size))print("SM:")# 计算E(a+ra)、E(b+rb)
    ra = random.randint(0, N)
    rb = random.randint(0, N)print("1 已收到来自客户端的E(a)和E(B),随机 ra =", ra,"rb =", rb)# e1:E(a)+E(ra)=E(a+ra)  e2:E(b)+E(rb)=E(b+rb)
    e1 = Ea+ra
    e2 = Eb+rb
    # e3:E(a)×ra=E(a×ra) e4:E(b)×rb=E(b×rb) e5:E(ra)×rb=E(ra×rb)
    e3 = Ea*rb
    e4 = Eb*ra
    e5 = pub_key.encrypt(ra)*rb

    # 将E(a+ra)、E(b+rb)传送给客户端
    conn.sendall(pickle.dumps((e1, e2)))print("2 计算E(a+ra)、E(b+rb),传输给客户端")# 获取客户端传来的E[(a+ra)×(b+rb)],得到E(a×b)
    d = pickle.loads(conn.recv(size))print("3 获取客户端传来的E[(a+ra)×(b+rb)]")
    e = d-e3-e4-e5
    conn.sendall(pickle.dumps(e))print("4 计算E(a×b)=E[(a+ra)×(b+rb)-a×ra-b×rb-ra×rb],传给客户端\n")return e

if __name__ =='__main__':# 开启连接
    ip_port =('127.0.0.1',9999)
    sk = socket.socket()# 创建套接字
    sk.bind(ip_port)# 绑定服务地址
    sk.listen(5)# 监听连接请求print('启动socket服务，等待客户端连接...\n')
    conn, address = sk.accept()# 等待连接，此处自动阻塞
    size =204800
    N =1000
    string ="========================================================\n"
    pub_key = pickle.loads(conn.recv(size))print("收到来自服务器的公钥：", pub_key)# 一、验证SM算法print(string+"一、验证SM算法\n"+string)
    e = SM()

• P2代码

defSM(Ea, Eb):print("SM:")# 向服务器发送数据
    s.sendall(pickle.dumps((Ea, Eb)))# 收到来自服务器的E(a+ra)、E(b+rb)
    e1, e2 = pickle.loads(s.recv(size))print("1 收到来自服务器的E(a+ra)、E(b+rb)")# 用私钥解得a+ra、b+rb，并加密
    d1 = private_key.decrypt(e1)
    d2 = private_key.decrypt(e2)
    d = pub_key.encrypt(d1*d2)print("2 解密得 a+ra =", d1," 和 b+rb =", d2)
    s.sendall(pickle.dumps(d))print("3 向服务器发送E[(a+ra)×(b+rb)]")# 验证结果
    e = pickle.loads(s.recv(size))print("4 收到来自服务器的E(a×b)")print("验证结果:\na =", private_key.decrypt(
        Ea),"b =", private_key.decrypt(Eb))print("解密a×b =", private_key.decrypt(e),"\n")if __name__ =='__main__':
    ip_port =('127.0.0.1',9999)
    s = socket.socket()# 创建套接字
    s.connect(ip_port)# 连接服务器
    paillier.DEFAULT_KEYSIZE =512
    size =204800
    N =512# 生成公私钥
    pub_key, private_key = paillier.generate_paillier_keypair()
    string ="========================================================\n"
    s.sendall(pickle.dumps(pub_key))print("将公钥发送给服务器:", pub_key)# 一、验证SM算法print(string+"一、验证SM算法\n"+string)
    a = random.randint(0, N)
    b = random.randint(0, N)# 生成E(a)和E(b)
    Ea = pub_key.encrypt(a)
    Eb = pub_key.encrypt(b)print("已知a =", a,"b =", b)
    SM(Ea, Eb)

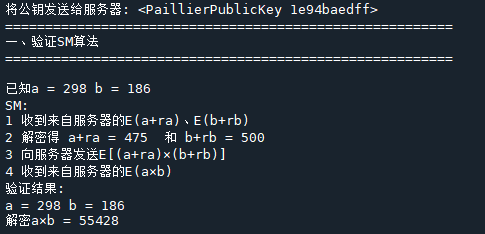
3.3 验证结果

• P1

• P2

4、实现并验证 SSED 算法

4.1 SSED目标

在SSED算法中，P1拥有两个加密向量E(X)={E(x1),E(x2)…E(xm)}和E(Y)={E(y1),E(y2)…E(ym)}，P2拥有私钥

• 算法目标：P1 想要计算 E p k ( ∣ X − Y ∣ 2 ) E_{p k}\left(|X-Y|^{2}\right) Epk​(∣X−Y∣2)

4.2 计算过程

依次得到（Xi-Yi），运行SM()算法后对结果求和

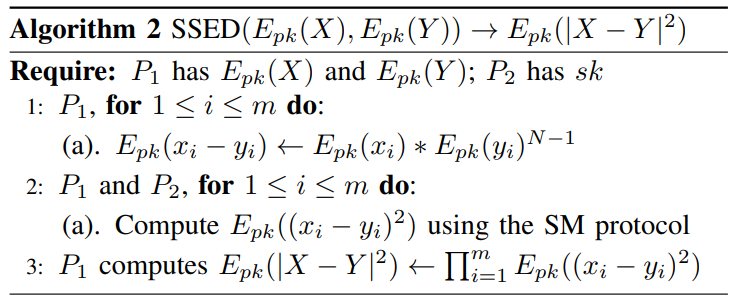
• P1代码

defSM():...return e

defSSED():
    m = pickle.loads(conn.recv(size))
    e =[SM()for i inrange(m)]
    conn.sendall(pickle.dumps(e))
    ed = pickle.loads(conn.recv(size))# 二、验证SSED算法print(string+"二、验证SSED算法\n"+string)
SSED()

• P2代码

defSM():...defSSED(m):# 生成长度为m的X和Y向量，并加密得到E(X)和E(Y)
    X = random.uniform(0, N)
    Y = random.uniform(0, N)print("已知\nX =", X,"\nY =", Y,"\n")
    s.sendall(pickle.dumps(m))for i inrange(m):
        a = X[i]-Y[i]
        Ea = pub_key.encrypt(a)
        SM(Ea, Ea)
    e = pickle.loads(s.recv(size*m))
    s.sendall(pickle.dumps(1))# 表示已经收到消息
    e_de =[private_key.decrypt(i)for i in e]print("验证结果:\n(Xi-Yi)^2 =", e_de)print("解密 𝐸[(𝑋−𝑌)^2] =", private_key.decrypt(sum(e)),"\n")# 二、验证SSED算法print(string+"二、验证SSED算法\n"+string)
m =2# X、Y的列表长度
SSED(m)

4.3 验证结果

• P1

• P2

5、实现并验证 SBD 算法

5.1 SBD目标

在SBD算法中，P1拥有一个加密x，P2拥有私钥

• 算法目标：P1 想要由E(x)得到 ⟨ E ( x 0 ) , … , E ( x m − 1 ) ⟩ \left\langle E\left(x_{0}\right), \ldots, E\left(x_{m-1}\right)\right\rangle ⟨E(x0​),…,E(xm−1​)⟩

序列内分别为x从高位至低位的二进制表示的加密结果。

5.2 计算过程

此处涉及到三个函数内容：

• SBD

• Encrypted_LSB

• SVR

• P1代码

defSM():...return e

defEncrypted_LSB(pub_key, T, i):
    r = random.randint(0, N)print("r=", r)
    Y = T+pub_key.encrypt(r)# 将Y发送给客户端
    conn.sendall(pickle.dumps(Y))print("1.1 LSB-将Y传输给客户端")
    a = pickle.loads(conn.recv(size))print("1.2 LSB-收到来自客户端的α")if r %2==0:
        xi = a
    else:
        xi = pub_key.encrypt(1)-a
    print("1.3 LSB-得到E(x%d)"% i)return xi

defSVR(Ex, EX, m):
    temp =[EX[i]*(2**i)for i inrange(m)]
    U =sum(temp)
    V = U-Ex
    r = random.randint(0, N)
    W = V*r
    conn.sendall(pickle.dumps(W))print("3.1 SVR-将W传输给客户端")
    r = pickle.loads(conn.recv(size))print("3.2 SVR-收到来自客户端的r")return r

defSBD(m, x):print("SBD:")
    l =2**(-1)print("m =", m,'x =', x)whileTrue:
        T = pub_key.encrypt(x)
        EX =[]for i inrange(m):
            Exi = Encrypted_LSB(pub_key, T, i)
            EX.append(Exi)
            Z = T-Exi
            T = Z*l
        print("2 完成E(xi)和T的计算")
        r = SVR(pub_key.encrypt(x), EX, m)if r ==1:
            conn.sendall(pickle.dumps(0))breakelse:
            conn.sendall(pickle.dumps(1))return EX

# 三、验证SBD算法print(string+"三、验证SBD算法\n"+string)
m =3# 0≤x≤2^m
x = random.randint(0,2**m-1)# 生成随机x
conn.sendall(pickle.dumps((m, x)))
EX = SBD(m, x)for i inrange(m):
    conn.sendall(pickle.dumps(EX[i]))print("4 将EX传输给客户端，验证结果\n")
temp = pickle.loads(conn.recv(size))# 表示收到

• P2代码

defSM():...defEncrypted_LSB():# 收到来自服务器的Y
    Y = pickle.loads(s.recv(size))print("1.1 LSB-收到来自服务器的Y")
    y = private_key.decrypt(Y)if y %2==0:
        a = pub_key.encrypt(0)else:
        a = pub_key.encrypt(1)
    s.sendall(pickle.dumps(a))print("1.2 LSB-y =", y,",将 α 发送给服务器")defSVR():
    W = pickle.loads(s.recv(size))print("3.1 SVR-收到来自服务器的W")if private_key.decrypt(W)==0:
        r =1else:
        r =0
    s.sendall(pickle.dumps(r))print("3.2 SVR-将r发送给服务器\n")defSBD(m):print("SBD:")whileTrue:for i inrange(m):
            Encrypted_LSB()print("2 等待客户端完成E(xi)和T的计算")
        SVR()
        flag = pickle.loads(s.recv(size))if flag ==0:break# 三、验证SBD算法print(string+"三、验证SBD算法\n"+string)
m, x = pickle.loads(s.recv(size))print("已知m =", m,"x =", x)
SBD(m)
EX =[pickle.loads(s.recv(size))for i inrange(m)]print("4 收到来自服务器的EX\n")
s.sendall(pickle.dumps(1))# 表示收到
DEX =[private_key.decrypt(xi)for xi in EX]
DEX_rev =list(reversed(DEX))print("验证结果:\nm =", m,"x =", x)print("EX =", DEX_rev,"\n")

5.3 验证结果

• P1

• P2

6、实现并验证 SMIN 算法

6.1 SMIN目标

在SMIN算法中，P1拥有由SBD算法得到的u、v两个数值的加密二进制表示，即[u]、[v]，且形式如下：

     [
    
    
     z
    
    
     ]
    
    
     =
    
    
     
      ⟨
     
     
      
       E
      
      
       
        p
       
       
        k
       
      
     
     
      
       (
      
      
       
        z
       
       
        1
       
      
      
       )
      
     
     
      ,
     
     
      …
     
     
      ,
     
     
      
       E
      
      
       
        p
       
       
        k
       
      
     
     
      
       (
      
      
       
        z
       
       
        l
       
      
      
       )
      
     
     
      ⟩
     
    
   
   
     [z]=\left\langle E_{p k}\left(z_{1}\right), \ldots, E_{p k}\left(z_{l}\right)\right\rangle 
   
  
 [z]=⟨Epk​(z1​),…,Epk​(zl​)⟩

P2拥有私钥。

• 算法目标：P1 想要由[u]、[v]得到 [min(u,v)]

6.2 计算过程

此处涉及到SM函数和SBD函数，同时需要实现SMIN函数。

下图中需要掌握的几个符号含义：

1. F：随机生成的标志，表示初始认为 u > v 或 v ≥ u
2. 异或运算： o 1 ⊕ o 2 = o 1 + o 2 − 2 ( o 1 ∗ o 2 ) o_{1} \oplus o_{2}=o_{1}+o_{2}-2\left(o_{1} * o_{2}\right) o1​⊕o2​=o1​+o2​−2(o1​∗o2​) 在加密算法中即： G i = E p k ( u i ) ∗ E p k ( v i ) ∗ E p k ( u i ∗ v i ) N − 2 G_{i}=E_{p k}\left(u_{i}\right) * E_{p k}\left(v_{i}\right) * E_{p k}\left(u_{i} * v_{i}\right)^{N-2} Gi​=Epk​(ui​)∗Epk​(vi​)∗Epk​(ui​∗vi​)N−2

3.                                                      π                                  1                                                  \pi_{1}                         π1​代表一个随机映射函数。
   

• SMIN

• P1代码

defSM():...return e

defSBD(m, x):...return EX
    
defRandom_Function(l1):
    l2 = l1.copy()
    random.shuffle(l2)returndict(zip(l1, l2))defSMIN(m, u, v):
    F =[random.random()for i inrange(m)]print("m =", m,'u =', u,'v =', v)
    EU = SBD(m, u)# 获得[u],[v]
    EU.reverse()
    EV = SBD(m, v)
    EV.reverse()
    EUV, W, T, G, H, FAI, L =[],[],[],[],[],[],[]
    H.append(pub_key.encrypt(0))
    r =[random.randint(0, N)for i inrange(m)]for i inrange(m):
        conn.sendall(pickle.dumps((EU[i], EV[i])))print("(1) 将EU["+str(i)+"]、EV["+str(i)+"]传输给客户端")
        r2 = random.randint(0, N)
        r3 = random.randint(0, N)print("r1 =", r[i],"r2 =", r2,"r3 =", r3)
        EUV.append(SM())if F[i]>=0.5:
            W.append(EU[i]-EUV[i])
            T.append(EV[i]-EU[i]+pub_key.encrypt(r[i]))else:
            W.append(EV[i]-EUV[i])
            T.append(EU[i]-EV[i]+pub_key.encrypt(r[i]))
        G.append(EU[i]+EV[i]-2*EUV[i])

        H.append(H[i]*r2+G[i])
        FAI.append(pub_key.encrypt(-1)+H[i+1])
        L.append(W[i]+FAI[i]*r3)
    len_ls =list(range(m))
    mp1 = Random_Function(len_ls)
    mp2 = Random_Function(len_ls)
    T2, L2 =[0]*m,[0]*m
    for i inrange(m):# 根据键映射值
        T2[mp1[i]]= T[i]
        L2[mp2[i]]= L[i]for i inrange(m):
        conn.sendall(pickle.dumps(T2[i]))
        conn.sendall(pickle.dumps(L2[i]))print("(2) 将Γ’、L’传输给客户端")
    a = pickle.loads(conn.recv(size))
    M2 = pickle.loads(conn.recv(size))print("(3) 收到来自客户端的E(α)和 M’")
    M3 =[0]*m
    for i inrange(m):# 根据值反得到键
        idex =list(mp1.keys())[list(mp1.values()).index(i)]
        M3[idex]= M2[i]
    lamda, EMIN =[],[]for i inrange(m):
        lamda.append(M3[i]-a*r[i])if F[i]>=0.5:
            EMIN.append(EU[i]+lamda[i])else:
            EMIN.append(EV[i]+lamda[i])return EMIN

# 四、验证SMIN算法print(string+"四、验证SMIN算法\n"+string)
m =5
u = random.randint(0,2**m-1)# 生成随机数u,v
v = random.randint(0,2**m-1)# u,v=6,24
conn.sendall(pickle.dumps((m, u, v)))print("1.1 将m传输给客户端")
EMIN = SMIN(m, u, v)for i inrange(m):
    conn.sendall(pickle.dumps(EMIN[i]))print("(4)将EMIN传输给客户端，验证结果\n")

• P2代码

defSM():...passdefSBD(m):...passdefSMIN(m):
    SBD(m)
    SBD(m)for i inrange(m):
        ui, vi = pickle.loads(s.recv(size))print("(1) 收到来自服务器的EU["+str(i)+"]、EV["+str(i)+"]")
        SM(ui, vi)
    T2, L2 =[],[]for i inrange(m):
        T2.append(pickle.loads(s.recv(size)))
        L2.append(pickle.loads(s.recv(size)))print("(2) 收到来自服务器的Γ’、L’")
    M =[private_key.decrypt(L2[i])for i inrange(m)]if1in M:
        a =1else:
        a =0print("α =", a)
    M2 =[T2[i]*a for i inrange(m)]
    s.sendall(pickle.dumps(pub_key.encrypt(a)))
    s.sendall(pickle.dumps(M2))print("(3) 将E(α)和 M’发送给服务器")# 四、验证SMIN算法print(string+"四、验证SMIN算法\n"+string)
m, u, v = pickle.loads(s.recv(size))print("已知m =", m,"u =", u,"v =", v)
SMIN(m)
EMIN =[pickle.loads(s.recv(size))for i inrange(m)]print("(4)收到来自服务器的EMIN\n")
DEMIN =[private_key.decrypt(xi)for xi in EMIN]# DEMIN_res=list(reversed(DEMIN))
ans =int("".join(str(i)for i in DEMIN),2)print("验证结果:\nm =", m,"u =", u,"v =", v)print("EMIN =", DEMIN)print("MIN =", ans,"\n")

6.3 验证结果

• P1

• P2

7、自定义任务——安全汉明距离

7.1 SMIN目标

汉明距离是使用在数据传输差错控制编码里面的，汉明距离是一个概念，它表示两个（相同长度）字符串对应位置的不同字符的数量，我们以d（x,y）表示两个字x,y之间的汉明距离。对两个字符串进行异或运算，并统计结果为1的个数，那么这个数就是汉明距离。

在安全汉明距离中，需要将两个数字 x、y 转为二进制加密表示（SBD算法），对加密内容进行异或运算计算每位二进制之间的距离，距离之和即为汉明距离。

• 算法目标：P1 想要由[x]、[y]得到汉明距离
• 异或算法： o 1 ⊕ o 2 = o 1 + o 2 − 2 ( o 1 ∗ o 2 ) o_{1} \oplus o_{2}=o_{1}+o_{2}-2\left(o_{1} * o_{2}\right) o1​⊕o2​=o1​+o2​−2(o1​∗o2​) G i = E p k ( u i ) ∗ E p k ( v i ) ∗ E p k ( u i ∗ v i ) N − 2 G_{i}=E_{p k}\left(u_{i}\right) * E_{p k}\left(v_{i}\right) * E_{p k}\left(u_{i} * v_{i}\right)^{N-2} Gi​=Epk​(ui​)∗Epk​(vi​)∗Epk​(ui​∗vi​)N−2

7.2 计算过程

1. 已知数字a、b，通过SBD将其转为二进制表示
2. 对二进制序列异或运算
3. 对异或运算结果相加，解密看答案是否正确

• P1代码

defSM():...return e

defSBD(m, x):...return EX
    
defHamming(m, a, b):
    conn.sendall(pickle.dumps(m))
    EA = SBD(m, a)
    EA.reverse()
    EB = SBD(m, b)
    EB.reverse()
    conn.sendall(pickle.dumps((EA, EB)))
    EAB =[SM()for i inrange(m)]
    XOR =[EA[i]+EB[i]-2*EAB[i]for i inrange(m)]
    conn.sendall(pickle.dumps(XOR))# 五、汉明距离计算print(string+"五、汉明距离计算\n"+string)
m =3# 二进制位数
a = random.randint(0,2**m-1)
b = random.randint(0,2**m-1)
conn.sendall(pickle.dumps((a, b)))
temp = pickle.loads(conn.recv(size))
Hamming(m, a, b)

• P2代码

defSM():...passdefSBD(m):...passdefHamming():
    m = pickle.loads(s.recv(size))
    SBD(m)
    SBD(m)
    EA, EB = pickle.loads(s.recv(size))
    DEA =[private_key.decrypt(xi)for xi in EA]
    DEB =[private_key.decrypt(xi)for xi in EB]for i inrange(m):
        SM(EA[i], EB[i])print("验证结果:\na =", a,"b =", b)print("二进制结果:\nA =", DEA,"\nB =", DEB)
    XOR = pickle.loads(s.recv(size))
    DXOR =[private_key.decrypt(xi)for xi in XOR]print("异或运算结果:", DXOR)print("汉明距离 =",sum(DXOR))# 五、汉明距离计算print(string+"五、汉明距离计算\n"+string)
a, b = pickle.loads(s.recv(size))
s.sendall(pickle.dumps(1))print("已知a =", a,"b =", b)
Hamming()

7.3 验证结果

• P1

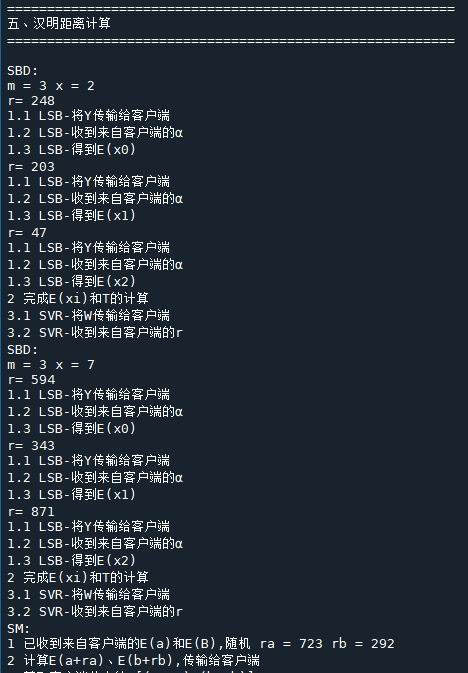
• P2

三、实验心得

1、传输问题——Pickle模块

在本实验过程中，由于在两端之间传输的数据为加密数据，无法按照传统的编码方式进行传输。需要调用Python中的Pickle模块。

参考链接：pickle.dumps()和pickle.loads()

假设连接为 s

• 传输 dumps

pub_key, private_key = paillier.generate_paillier_keypair()
s.sendall(pickle.dumps(pub_key))

• 接收 loads

pub_key=pickle.loads(s.recv(size))

参考链接：

socket编程python实现

pickle.dumps()和pickle.loads()