0
0

Golang每日一练(leetDay0049) 二叉树专题（9）

二叉树专题（9）第146题除外

144. 二叉树的前序遍历 Binary-tree Preorder Traversal

给你二叉树的根节点 

root

，返回它节点值的 前序* *遍历。

示例 1：

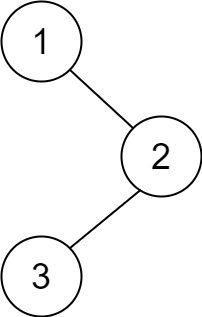
**输入：**root = [1,null,2,3]
**输出：**[1,2,3]

示例 2：

**输入：**root = []
**输出：**[]

示例 3：

**输入：**root = [1]
**输出：**[1]

示例 4：

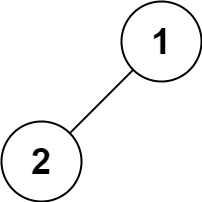
**输入：**root = [1,2]
**输出：**[1,2]

示例 5：

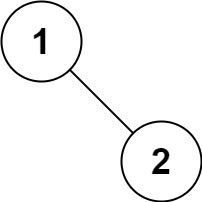
**输入：**root = [1,null,2]
**输出：**[1,2]

提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

公用的示例二叉树：

    3
   / \
  9  20
    /  \
   15   7

遍历结果：

前序遍历 preorder  = [3,9,20,15,7]
中序遍历 inorder   = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]

** 代码1：** 递归

package main

import (
    "fmt"
)

const null = -1 << 31

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func preorderTraversal(root *TreeNode) []int {
    var res []int
    preorder(root, &res)
    return res
}

func preorder(root *TreeNode, res *[]int) {
    if root == nil {
        return
    }
    *res = append(*res, root.Val)
    preorder(root.Left, res)
    preorder(root.Right, res)
}

func buildTree(nums []int) *TreeNode {
    if len(nums) == 0 {
        return nil
    }
    root := &TreeNode{Val: nums[0]}
    Queue := []*TreeNode{root}
    idx := 1
    for idx < len(nums) {
        node := Queue[0]
        Queue = Queue[1:]
        if nums[idx] != null {
            node.Left = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Left)
        }
        idx++
        if idx < len(nums) && nums[idx] != null {
            node.Right = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Right)
        }
        idx++
    }
    return root
}

func ArrayToString(arr []int) string {
    res := "["
    for i := 0; i < len(arr); i++ {
        res += fmt.Sprint(arr[i])
        if i != len(arr)-1 {
            res += ","
        }
    }
    return res + "]"
}

func main() {
    nums := []int{1, null, 2, 3}
    root := buildTree(nums)
    fmt.Println(ArrayToString(preorderTraversal(root)))
    nums = []int{3, 9, 20, null, null, 15, 7}
    root = buildTree(nums)
    fmt.Println(ArrayToString(preorderTraversal(root)))
}

** 代码2：** 迭代

package main

import (
    "fmt"
)

const null = -1 << 31

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func preorderTraversal(root *TreeNode) []int {
    var res []int
    if root == nil {
        return res
    }
    stack := []*TreeNode{}
    stack = append(stack, root)
    for len(stack) > 0 {
        cur := stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        res = append(res, cur.Val)
        if cur.Right != nil {
            stack = append(stack, cur.Right)
        }
        if cur.Left != nil {
            stack = append(stack, cur.Left)
        }
    }
    return res
}

func buildTree(nums []int) *TreeNode {
    if len(nums) == 0 {
        return nil
    }
    root := &TreeNode{Val: nums[0]}
    Queue := []*TreeNode{root}
    idx := 1
    for idx < len(nums) {
        node := Queue[0]
        Queue = Queue[1:]
        if nums[idx] != null {
            node.Left = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Left)
        }
        idx++
        if idx < len(nums) && nums[idx] != null {
            node.Right = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Right)
        }
        idx++
    }
    return root
}

func ArrayToString(arr []int) string {
    res := "["
    for i := 0; i < len(arr); i++ {
        res += fmt.Sprint(arr[i])
        if i != len(arr)-1 {
            res += ","
        }
    }
    return res + "]"
}

func main() {
    nums := []int{1, null, 2, 3}
    root := buildTree(nums)
    fmt.Println(ArrayToString(preorderTraversal(root)))
    nums = []int{3, 9, 20, null, null, 15, 7}
    root = buildTree(nums)
    fmt.Println(ArrayToString(preorderTraversal(root)))
}

输出：

[1,2,3]
[3,9,20,15,7]

145. 二叉树的后序遍历 Binary-tree Postorder Traversal

给你一棵二叉树的根节点 

root

，返回其节点值的 **后序遍历 **。

示例 1：

**输入：**root = [1,null,2,3]
**输出：**[3,2,1]

示例 2：

**输入：**root = []
**输出：**[]

示例 3：

**输入：**root = [1]
**输出：**[1]

提示：

  • 树中节点的数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

** 代码1：** 递归

package main

import (
    "fmt"
)

const null = -1 << 31

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func postorderTraversal(root *TreeNode) []int {
    var res []int
    postorder(root, &res)
    return res
}

func postorder(root *TreeNode, res *[]int) {
    if root == nil {
        return
    }
    postorder(root.Left, res)
    postorder(root.Right, res)
    *res = append(*res, root.Val)
}

func buildTree(nums []int) *TreeNode {
    if len(nums) == 0 {
        return nil
    }
    root := &TreeNode{Val: nums[0]}
    Queue := []*TreeNode{root}
    idx := 1
    for idx < len(nums) {
        node := Queue[0]
        Queue = Queue[1:]
        if nums[idx] != null {
            node.Left = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Left)
        }
        idx++
        if idx < len(nums) && nums[idx] != null {
            node.Right = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Right)
        }
        idx++
    }
    return root
}

func ArrayToString(arr []int) string {
    res := "["
    for i := 0; i < len(arr); i++ {
        res += fmt.Sprint(arr[i])
        if i != len(arr)-1 {
            res += ","
        }
    }
    return res + "]"
}

func main() {
    nums := []int{1, null, 2, 3}
    root := buildTree(nums)
    fmt.Println(ArrayToString(postorderTraversal(root)))
    nums = []int{3, 9, 20, null, null, 15, 7}
    root = buildTree(nums)
    fmt.Println(ArrayToString(postorderTraversal(root)))
}

** 代码2：** 迭代

package main

import (
    "fmt"
)

const null = -1 << 31

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func postorderTraversal(root *TreeNode) []int {
    var res []int
    if root == nil {
        return res
    }
    stack := []*TreeNode{}
    stack = append(stack, root)
    for len(stack) > 0 {
        cur := stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        res = append([]int{cur.Val}, res...)
        if cur.Left != nil {
            stack = append(stack, cur.Left)
        }
        if cur.Right != nil {
            stack = append(stack, cur.Right)
        }
    }
    return res
}

func buildTree(nums []int) *TreeNode {
    if len(nums) == 0 {
        return nil
    }
    root := &TreeNode{Val: nums[0]}
    Queue := []*TreeNode{root}
    idx := 1
    for idx < len(nums) {
        node := Queue[0]
        Queue = Queue[1:]
        if nums[idx] != null {
            node.Left = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Left)
        }
        idx++
        if idx < len(nums) && nums[idx] != null {
            node.Right = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Right)
        }
        idx++
    }
    return root
}

func ArrayToString(arr []int) string {
    res := "["
    for i := 0; i < len(arr); i++ {
        res += fmt.Sprint(arr[i])
        if i != len(arr)-1 {
            res += ","
        }
    }
    return res + "]"
}

func main() {
    nums := []int{1, null, 2, 3}
    root := buildTree(nums)
    fmt.Println(ArrayToString(postorderTraversal(root)))
    nums = []int{3, 9, 20, null, null, 15, 7}
    root = buildTree(nums)
    fmt.Println(ArrayToString(postorderTraversal(root)))
}

输出：

[3,2,1]
[9,15,7,20,3]

对比： 94. 二叉树的中序遍历 Binary-tree Inorder Traversal

给定一个二叉树的根节点 

root

，返回 它的 中序 遍历 。

示例 1：

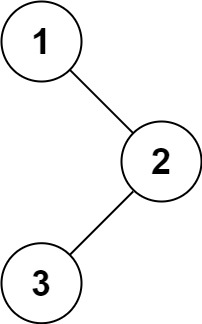
**输入：**root = [1,null,2,3]
**输出：**[1,3,2]

示例 2：

**输入：**root = []
**输出：**[]

示例 3：

**输入：**root = [1]
**输出：**[1]

提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

代码1： 递归法

package main

import (
    "fmt"
)

const null = -1 << 31

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func inorderTraversal(root *TreeNode) []int {
    var res []int
    inorder(root, &res)
    return res
}

func inorder(root *TreeNode, res *[]int) {
    if root == nil {
        return
    }
    inorder(root.Left, res)
    *res = append(*res, root.Val)
    inorder(root.Right, res)
}

func buildTree(nums []int) *TreeNode {
    if len(nums) == 0 {
        return nil
    }
    root := &TreeNode{Val: nums[0]}
    Queue := []*TreeNode{root}
    idx := 1
    for idx < len(nums) {
        node := Queue[0]
        Queue = Queue[1:]
        if nums[idx] != null {
            node.Left = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Left)
        }
        idx++
        if idx < len(nums) && nums[idx] != null {
            node.Right = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Right)
        }
        idx++
    }
    return root
}

func ArrayToString(arr []int) string {
    res := "["
    for i := 0; i < len(arr); i++ {
        res += fmt.Sprint(arr[i])
        if i != len(arr)-1 {
            res += ","
        }
    }
    return res + "]"
}

func main() {
    nums := []int{1, null, 2, 3}
    root := buildTree(nums)
    fmt.Println(ArrayToString(inorderTraversal(root)))
    nums = []int{3, 9, 20, null, null, 15, 7}
    root = buildTree(nums)
    fmt.Println(ArrayToString(inorderTraversal(root)))
}

代码2： 迭代法

package main

import (
    "fmt"
)

const null = -1 << 31

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func inorderTraversal(root *TreeNode) []int {
    var res []int
    stack := []*TreeNode{}
    cur := root
    for cur != nil || len(stack) > 0 {
        for cur != nil {
            stack = append(stack, cur)
            cur = cur.Left
        }
        cur = stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        res = append(res, cur.Val)
        cur = cur.Right
    }
    return res
}

func buildTree(nums []int) *TreeNode {
    if len(nums) == 0 {
        return nil
    }
    root := &TreeNode{Val: nums[0]}
    Queue := []*TreeNode{root}
    idx := 1
    for idx < len(nums) {
        node := Queue[0]
        Queue = Queue[1:]
        if nums[idx] != null {
            node.Left = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Left)
        }
        idx++
        if idx < len(nums) && nums[idx] != null {
            node.Right = &TreeNode{Val: nums[idx]}
            Queue = append(Queue, node.Right)
        }
        idx++
    }
    return root
}

func ArrayToString(arr []int) string {
    res := "["
    for i := 0; i < len(arr); i++ {
        res += fmt.Sprint(arr[i])
        if i != len(arr)-1 {
            res += ","
        }
    }
    return res + "]"
}

func main() {
    nums := []int{1, null, 2, 3}
    root := buildTree(nums)
    fmt.Println(ArrayToString(inorderTraversal(root)))
    nums = []int{3, 9, 20, null, null, 15, 7}
    root = buildTree(nums)
    fmt.Println(ArrayToString(inorderTraversal(root)))
}

输出：

[1,3,2]
[9,3,15,20,7]

三种遍历的递归对比

“根左右、左根右、左右根”

func preorder(root *TreeNode, res *[]int) {
    *res = append(*res, root.Val)
    preorder(root.Left, res)
    preorder(root.Right, res)
}

func inorder(root *TreeNode, res *[]int) {
    inorder(root.Left, res)
    *res = append(*res, root.Val)
    inorder(root.Right, res)
}

func postorder(root *TreeNode, res *[]int) {
    postorder(root.Left, res)
    postorder(root.Right, res)
    *res = append(*res, root.Val)
}

三种遍历的迭代对比

注意左、右子节点的压栈顺序，以及后序结果中的“追加”实为“前插”

func preorderTraversal(root *TreeNode) []int {
    var res []int
    if root == nil {
        return res
    }
    stack := []*TreeNode{}
    stack = append(stack, root)
    for len(stack) > 0 {
        cur := stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        res = append(res, cur.Val)
        if cur.Right != nil {
            stack = append(stack, cur.Right)
        }
        if cur.Left != nil {
            stack = append(stack, cur.Left)
        }
    }
    return res
}

func inorderTraversal(root *TreeNode) []int {
    var res []int
    stack := []*TreeNode{}
    cur := root
    for cur != nil || len(stack) > 0 {
        for cur != nil {
            stack = append(stack, cur)
            cur = cur.Left
        }
        cur = stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        res = append(res, cur.Val)
        cur = cur.Right
    }
    return res
}

func postorderTraversal(root *Treecur) []int {
    var res []int
    if root == nil {
        return res
    }
    stack := []*Treecur{}
    stack = append(stack, root)
    for len(stack) > 0 {
        cur := stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        res = append([]int{cur.Val}, res...)
        if cur.Left != nil {
            stack = append(stack, cur.Left)
        }
        if cur.Right != nil {
            stack = append(stack, cur.Right)
        }
    }
    return res
}

146. LRU缓存 LRU Cache

请你设计并实现一个满足​ LRU (最近最少使用) 缓存 ​约束的数据结构。

实现 

LRUCache

类：

  • LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
  • int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
  • void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 

get

和 

put

必须以 

O(1)

的平均时间复杂度运行。

示例：

**输入**
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
**输出**
[null, null, null, 1, null, -1, null, -1, 3, 4]

**解释**
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

提示：

  • 1 <= capacity <= 3000
  • 0 <= key <= 10000
  • 0 <= value <= 10^5
  • 最多调用 2 * 10^5 次 get 和 put

** 代码：**

type LRUCache struct {
    capacity int
    cache    map[int]*list.Element
    list     *list.List
}

type pair struct {
    key   int
    value int
}

func Constructor(capacity int) LRUCache {
    return LRUCache{
        capacity: capacity,
        cache:    make(map[int]*list.Element),
        list:     list.New(),
    }
}

func (c *LRUCache) Get(key int) int {
    if elem, ok := c.cache[key]; ok {
        c.list.MoveToFront(elem)
        return elem.Value.(*pair).value
    }
    return -1
}

func (c *LRUCache) Put(key int, value int) {
    if elem, ok := c.cache[key]; ok {
        elem.Value.(*pair).value = value
        c.list.MoveToFront(elem)
    } else {
        if c.list.Len() == c.capacity {
            // remove the least recently used element
            tailElem := c.list.Back()
            delete(c.cache, tailElem.Value.(*pair).key)
            c.list.Remove(tailElem)
        }
        // insert new element to front
        newElem := c.list.PushFront(&pair{key, value})
        c.cache[key] = newElem
    }
}

输出：

略

🌟 每日一练刷题专栏 🌟

✨持续，努力奋斗做强刷题搬运工！

👍 点赞，你的认可是我坚持的动力！

🌟 收藏，你的青睐是我努力的方向！

✎ 评论，你的意见是我进步的财富！

☸ 主页：https://hannyang.blog.csdn.net/

Golang每日一练 专栏

Python每日一练 专栏

C/C++每日一练 专栏

Java每日一练 专栏

标签： golang leetcode 二叉树
本文转载自: https://blog.csdn.net/boysoft2002/article/details/130405241
版权归原作者 Hann Yang 所有， 如有侵权，请联系我们删除。
登录后发布评论

“Golang每日一练(leetDay0049) 二叉树专题（9）”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

rabbitMQ

web渗透测试漏洞复现：Springboot Actuator未授权漏洞复现

如何给SaaS应用做安全

【软件测试】自动化常用函数

postman变量和脚本功能介绍

Python Selenium常见的报错以及措施

idea导出配置文件

文章导航