文章目录
优化器在机器学习、深度学习中往往起着举足轻重的作用,同一个模型,因选择不同的优化器,性能有可能相差很大,甚至导致一些模型无法训练。所以了解各种优化器的基本原理非常重要。下面介绍各种常用优化器或算法的主要原理,及各自的优点或不足。
3.1、传统梯度优化的不足(BGD,SGD,MBGD)
BGD、SGD、MBGD分别为批量梯度下降算法、随机梯度下降算法、小批量梯度下降算法。BGD在训练的时候选用所有的训练集进行计算,SGD在训练的时候只选择一个数据进行训练,而MBGD在训练的时候只选择小部分数据进行训练。这三个优化算法在训练的时候虽然所采用的的数据量不同,但是他们在进行参数优化的时候是相同的。
在训练的时候一般都是使用小批量梯度下降算法,即选择部分数据进行训练,在此把这三种算法统称为传统梯度更新算法,因为他们在更新参数的时候采用相同的方式,而更优的优化算法从梯度方向和学习率方面对参数更新方式进行优化。
传统梯度更新算法为最常见、最简单的一种参数更新策略。其基本思想是:先设定一个学习率
λ
\lambda
λ,参数沿梯度的反方向移动。假设需要更新的参数为
θ
\theta
θ,梯度为
g
g
g,则其更新策略可表示为:
θ
←
θ
−
λ
g
\theta \leftarrow \theta-\lambda g
θ←θ−λg
这种梯度更新算法简洁,当学习率取值恰当时,可以收敛到全面最优点(凸函数)或局部最优点(非凸函数)。但其还有很大的不足点:
- 对超参数学习率比较敏感(过小导致收敛速度过慢,过大又越过极值点)。
- 学习率除了敏感,有时还会因其在迭代过程中保持不变,很容易造成算法被卡在鞍点的位置。
- 在较平坦的区域,由于梯度接近于0,优化算法会因误判,在还未到达极值点时,就提前结束迭代,陷入局部极小值。
3.1.1 一维梯度下降
下面展示如何实现梯度下降以及上述这些不足点。为了简单,选用目标函数
f
(
x
)
=
x
2
f(x)=x^2
f(x)=x2。尽管我们知道
x
=
0
x=0
x=0时
f
(
x
)
f(x)
f(x)能取得最小值(这里x为模型参数)。
import numpy as np
import torch
from d2l import torch as d2l
%matplotlib inline
#目标函数deff(x):return x**2#目标函数的梯度(导数)deff_grad(x):return2*x
接下来,使用
x
=
10
x=10
x=10作为初始值,并假设
η
=
0.2
\eta=0.2
η=0.2。使用梯度下降迭代法迭代
x
x
x共10次,可以看到
x
x
x的值最终将接近最优解。
#进行梯度下降defgd(eta,f_grad):
x=10.0
results=[x]for i inrange(10):
x-=eta*f_grad(x)
results.append(float(x))print(f'epoch 10,x:{x:f}')return results
results = gd(0.2,f_grad)
epoch 10,x:0.060466
对
x
x
x优化的过程进行可视化。
defshow_trace(results,f):
n=max(abs(min(results)),abs(max(results)))
f_line=torch.arange(-n,n,0.01)
d2l.set_figsize()
d2l.plot([f_line,results],[[f(x)for x in f_line],[f(x)for x in results]],'x','f(x)',fmts=['-','-o'])
show_trace(results,f)
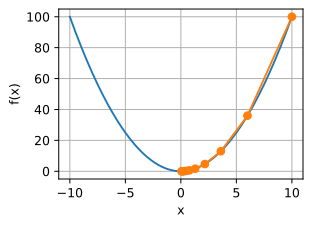
学习率
学习率决定了目标函数是否能够收敛到局部最小值,以及何时收敛到最小值。学习率
η
\eta
η可由算法设计者设置。请注意,如果使用的学习率太小,将导致
x
x
x的更新非常缓慢,需要更多的迭代。下面将学习率设置为0.05。如下图所示,尽管经历了10个步骤,我们仍然离最优解很远。
show_trace(gd(0.05,f_grad),f)
epoch 10,x:3.486784
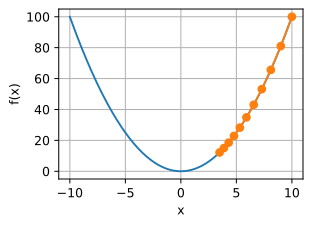
相反,当使用过高的学习率,
x
x
x的迭代不能保证降低
f
(
x
)
f(x)
f(x)的值,例如,当学习率为
η
=
1.1
\eta=1.1
η=1.1时,
x
x
x超出了最优解
x
=
0
x=0
x=0并逐渐发散。
show_trace(gd(1.1,f_grad),f)
epoch 10,x:61.917364
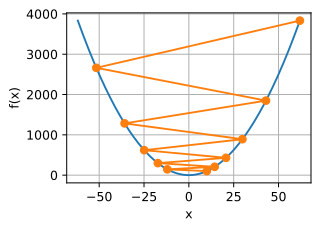
局部极小值
为了演示非凸函数的梯度下降,考虑函数
f
(
x
)
=
x
⋅
c
o
s
(
x
)
f(x)=x\cdot cos(x)
f(x)=x⋅cos(x),其中
c
c
c为某常数。这个函数有无穷多个最小值。如果学习率选择不当,我们最终只会得到一个最优解。下面的例子说明了高学习率如何导致较差的局部最小值。
f
′
(
x
)
=
c
o
s
(
c
x
)
−
c
∗
x
∗
s
i
n
(
c
x
)
f^{'}(x)=cos(cx)-c*x*sin(cx)
f′(x)=cos(cx)−c∗x∗sin(cx)
c=torch.tensor(0.15*np.pi)#目标函数deff(x):return x*torch.cos(c*x)#目标函数的梯度deff_grad(x):return torch.cos(c*x)-c*x*torch.sin(c*x)
show_trace(gd(2,f_grad),f)
epoch 10,x:-1.528166
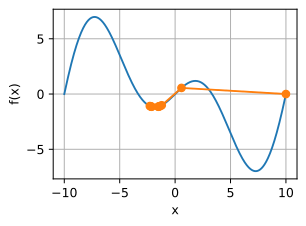
3.1.2 多维梯度下降
在对单元梯度下降有了了解之后,下面看看多元梯度下降,即考虑
x
=
[
x
1
,
x
2
,
⋯
,
x
d
]
T
x=[x_1,x_2,\cdots ,x_d]^T
x=[x1,x2,⋯,xd]T的情况。相应的它的梯度也是多元的,是一个由d个偏导数组成的向量:
∇
f
(
x
)
=
[
∂
f
x
∂
x
1
,
∂
f
x
∂
x
2
,
⋯
,
∂
f
x
∂
x
d
]
T
\nabla f(x)=[\frac{\partial f{x}}{\partial x_1},\frac{\partial f{x}}{\partial x_2},\cdots,\frac{\partial f{x}}{\partial x_d}]^T
∇f(x)=[∂x1∂fx,∂x2∂fx,⋯,∂xd∂fx]T
然后选择合适的学率进行梯度下降:
x
←
x
−
η
∇
f
(
x
)
x \leftarrow x-\eta \nabla f(x)
x←x−η∇f(x)
下面通过代码可视化它的参数更新过程。构造一个目标函数
f
(
x
)
=
x
1
2
+
2
x
2
2
f(x)=x_1^2+2x_2^2
f(x)=x12+2x22,并有二维向量
x
=
[
x
1
,
x
2
]
x=[x_1,x_2]
x=[x1,x2]作为输入,标量作为输出。梯度由
∇
f
(
x
)
=
[
2
x
1
,
4
x
2
]
T
\nabla f(x)=[2x_1,4x_2]^T
∇f(x)=[2x1,4x2]T给出。从初始位置[-5,-2]通过梯度下降观察x的轨迹。
首先需要定义两个辅助函数第一个是
train_2d()
函数,用指定的训练机优化2D目标函数;第二个是
show_trace_2d()
,用于显示x的轨迹。
#用指定的训练机优化2D目标函数deftrain_2d(trainer,steps=20,f_grad=None):
x1,x2,s1,s2=-5,-2,0,0
results=[(x1,x2)]for i inrange(steps):if f_grad:
x1,x2,s1,s2=trainer(x1,x2,s1,s2,f_grad)else:
x1,x2,s1,s2=trainer(x1,x2,s1,s2)
results.append((x1,x2))print(f'epoch{i+1},x1:{float(x1):f},x2:{float(x2):f}')return results
#显示优化过程中2D变量的轨迹defshow_trace_2d(f,results):
d2l.set_figsize()
d2l.plt.plot(*zip(*results),'-o',color='#ff7f0e')
x1,x2=torch.meshgrid(torch.arange(-5.5,1.0,0.1),
torch.arange(-3.0,1.0,0.1))
d2l.plt.contour(x1,x2,f(x1,x2),colors='#1f77b4')
d2l.plt.xlabel('x1')
d2l.plt.ylabel('x2')
接下来,使用学习率为
η
=
0.1
\eta=0.1
η=0.1时优化变量
x
x
x的轨迹。在经过20步时,
x
x
x的值接近其位于[0,0]的最小值。
#目标函数 deff_2d(x1,x2):return x1**2+2*x2**2#目标函数的梯度deff_2d_grad(x1,x2):return(2*x1,4*x2)#SGD更新参数defgd_2d(x1,x2,s1,s2,f_grad):
g1,g2=f_grad(x1,x2)return(x1-eta*g1,x2-eta*g2,0,0)
eta=0.1
show_trace_2d(f_2d,train_2d(gd_2d,f_grad=f_2d_grad))
epoch20,x1:-0.057646,x2:-0.000073
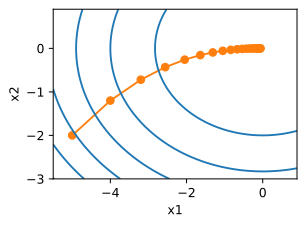
针对传统梯度优化算法的缺点,许多优化算法从梯度方向和学习率两方面入手。有些从梯度方向入手,如动量更新策略;而有些从学习率入手,这涉及调参问题;还有从两方面同时入手,如自适应更新策略。
在pytorch中使用传统的梯度下降算法可以使用
torch.optim.SGD
其格式为:
torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False,*, maximize=False)
因为使用的是传统的梯度下降算法,则
momentum
参数和
nesterov
参数默认即可不需要设置。下面看一看它的用法。
import torch
#改代码不可运行
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)#梯度清零
optimizer.zero_grad()
loss_fn(model(input), target).backward()#参数更新
optimizer.step()
3.2、动量(Momentum)
动量(Momentum)是模拟物理中动量的概念,具有物理上惯性的含义,一个物体在运动时具有惯性,把这个思想运用到梯度下降的计算中,可以增加算法的收敛速度和稳定性,具体实现如图所示: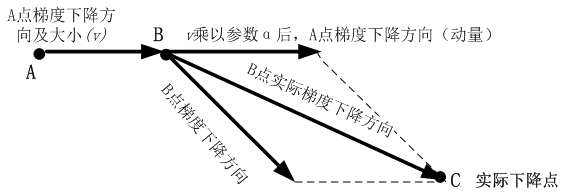
动量算法每下降一步都是由前面下降方向的一个累积和当前点梯度方向组合而成。含动量的随机梯度下降算法,其更新方式如下:
更
新
梯
度
:
g
^
←
1
b
a
t
c
h
_
s
i
z
e
∑
i
=
0
b
a
t
c
h
_
s
i
z
e
∇
θ
L
(
f
(
x
(
i
)
)
,
y
(
i
)
)
计
算
梯
度
:
v
←
β
v
+
g
更
新
参
数
:
θ
←
θ
−
η
v
更新梯度:\hat{g} \leftarrow \frac{1}{batch\_size} \sum_{i=0}^{batch\_size}\nabla_{\theta}L(f(x^{(i)}),y^{(i)})\\ 计算梯度:v \leftarrow \beta v+g\\ 更新参数:\theta \leftarrow \theta-\eta v
更新梯度:g^←batch_size1i=0∑batch_size∇θL(f(x(i)),y(i))计算梯度:v←βv+g更新参数:θ←θ−ηv
其中
β
\beta
β为动量参数,
η
\eta
η为学习率。
为了更好的观察动量带来的好处,使用一个新函数
f
(
x
)
=
0.1
x
1
2
+
2
x
2
2
f(x)=0.1x_1^2+2x_2^2
f(x)=0.1x12+2x22上使用不带动量的**传统梯度下降算法**观察下降过程。与上节的函数一样,f的最低水平为(0,0)。该函数在
x
1
x_1
x1方向上比较平坦,在此选择0.4的学习率。
import torch
from d2l import torch as d2l
%matplotlib inline
eta=0.4#目标函数 deff_2d(x1,x2):return0.1*x1**2+2*x2**2#sgd更新参数defgd_2d(x1,x2,s1,s2):return(x1-eta*0.2*x1,x2-eta*4*x2,0,0)
d2l.show_trace_2d(f_2d,d2l.train_2d(gd_2d))
epoch 20, x1: -0.943467, x2: -0.000073
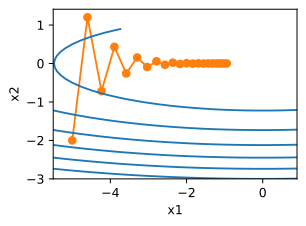
从结果来看,
x
2
x_2
x2方向的梯度比水平
x
1
x_1
x1方向的渐变高得多,变化快得多。因此就陷入了两个不可取的选择:如果选择较小的准确率。可以确保不会朝
x
2
x_2
x2方向发生偏离,但在
x
1
x_1
x1反向收敛会缓慢。如果学习率较高,
x
1
x_1
x1方向会收敛很快,但在
x
2
x_2
x2方向就不会向最优点靠近。下面将学习率从0.4调整到0.6。可以看出在
x
1
x_1
x1方向会有所改善,但是整体解决方案会很差。
eta=0.6
d2l.show_trace_2d(f_2d,d2l.train_2d(gd_2d))
epoch 20, x1: -0.387814, x2: -1673.365109
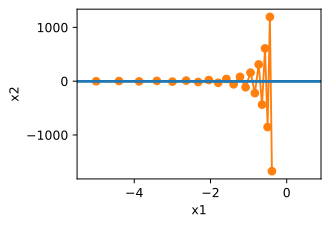
下面看一下使用动量算法在实践中的应用。
#动量法更新参数defmomentum_2d(x1,x2,v1,v2):
v1=beta*v1+0.2*x1
v2=beta*v2+4*x2
return x1-eta*v1,x2-eta*v2,v1,v2
eta,beta=0.6,0.5
d2l.show_trace_2d(f_2d,d2l.train_2d(momentum_2d))
epoch 20, x1: 0.007188, x2: 0.002553
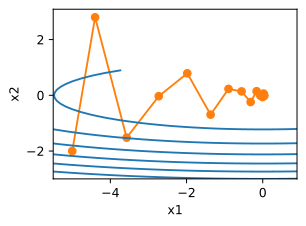
可见使用和之前一样的学习率,也能够很好的收敛,下面看看当降低动量参数时会发生啥。虽然将其减半到
β
=
0.25
\beta=0.25
β=0.25会导致一条几乎没有收敛的轨迹。但是也要比没有动力好很多。
eta,beta=0.6,0.25
d2l.show_trace_2d(f_2d,d2l.train_2d(momentum_2d))
epoch 20, x1: -0.126340, x2: -0.186632
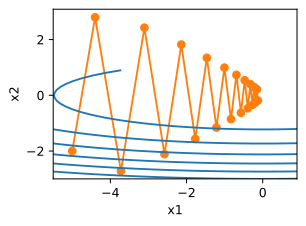
既然每一步都要将两个梯度方向(历史梯度、当前梯度)做一个合并再下降,因此可以按照前面一小步位置的“超前梯度”来做梯度合并。这样就可以先往前走一小步,在靠前一点的位置看到梯度,然后按照那个位置再来修正这一步的梯度方向,如下图所示。这样就得到动量算法的一种改进算法,称为Nesterov Accelerated Gradient,简称NAG算法。这种更新的算法能够防止大幅振荡,不会错过最小值,并会对参数更加敏感。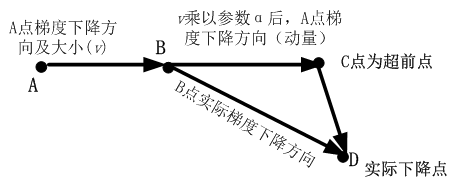
下面看看在pytorch中的使用:
torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False,*, maximize=False)
因为使用了动量,因此参数
momentum
就需要给定数值,
nesterov
设置为True时,将会使用NAG算法,它是动量算法的一种优化。
3.3、AdaGrad算法
AdaGrad算法是通过参数来调整合适的学习率,是能独立自动调整模型参数的学习率,对稀疏参数进行大幅更新和对频繁参数进行小幅更新,因此,AdaGrad方法非常适合处理稀疏数据。AdaGrad算法在某些深度学习模型上效果不错。但还是有些不足,可能是因其累积梯度平方导致学习率过早或过量的减少所致。以下是AdaGrad算法的更新步骤:
更
新
梯
度
:
g
^
←
1
b
a
t
c
h
_
s
i
z
e
∑
i
=
0
b
a
t
c
h
_
s
i
z
e
∇
θ
L
(
f
(
x
(
i
)
)
,
y
(
i
)
)
累
积
平
方
梯
度
:
r
←
r
+
g
^
⊙
g
^
计
算
参
数
:
△
θ
←
−
λ
δ
+
r
⊙
g
^
更
新
参
数
:
θ
←
θ
+
△
θ
更新梯度:\hat{g} \leftarrow \frac{1}{batch\_size} \sum_{i=0}^{batch\_size}\nabla_{\theta}L(f(x^{(i)}),y^{(i)})\\ 累积平方梯度:r \leftarrow r+\hat{g} \odot \hat{g}\\ 计算参数:\triangle \theta \leftarrow - \frac{\lambda}{\delta+\sqrt{r}}\odot \hat{g}\\ 更新参数:\theta \leftarrow \theta+\triangle \theta
更新梯度:g^←batch_size1i=0∑batch_size∇θL(f(x(i)),y(i))累积平方梯度:r←r+g^⊙g^计算参数:△θ←−δ+rλ⊙g^更新参数:θ←θ+△θ
其中
r
r
r为累积梯度变量,初始为0;
λ
\lambda
λ为学习率;
δ
\delta
δ为小参数,避免分母为0。
通过上述更新步骤可以看出:
- 随着迭代时间越长,累积梯度 r r r越大,导致学习速率 λ δ + r \frac{\lambda}{\delta+\sqrt{r}} δ+rλ随着时间较小,在接近目标值时,不会因为学习率过大而越过极值点。
- 不同参数之间的学习速率不同,因此,与之前固定学习率相比,不容易卡在鞍点。
- 如果梯度累积参数 r r r比较小,则速率会比较大,所以参数迭代的步长就会比较大。相反,如果梯度累积参数 r r r比较大,则速率会比较小,所以参数迭代的步长就会比较小。
下面使用和以前相同的问题:
f
(
x
)
=
0.1
x
1
2
+
2
x
2
2
f(x)=0.1x_1^2+2x_2^2
f(x)=0.1x12+2x22
将使用与之前相同的学习率来实施AdaGrad,即
η
=
0.4
\eta=0.4
η=0.4。
import math
import torch
from d2l import torch as d2l
%matplotlib inline
#adagrad更新参数defadagrad_2d(x1,x2,s1,s2):
eps=1e-6
g1,g2=0.2*x1,4*x2
s1+=g1**2
s2+=g2**2
x1-=eta/math.sqrt(s1+eps)*g1
x2-=eta/math.sqrt(s2+eps)*g2
return x1,x2,s1,s2
#目标函数deff_2d(x1,x2):return0.1*x1**2+2*x2**2
eta=0.4
d2l.show_trace_2d(f_2d,d2l.train_2d(adagrad_2d))
epoch 20, x1: -2.382563, x2: -0.158591
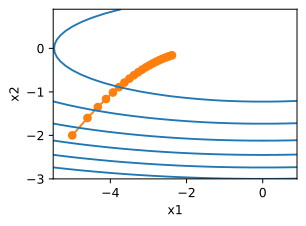
由结果来看,参数更新的过程变得平稳,但是由于梯度累积的越来越大,学习率持续下降,因此参数在后期阶段移动的不会那么多。现在我们适当的提高学习率到2,看看结果怎么样。
eta=2
d2l.show_trace_2d(f_2d,d2l.train_2d(adagrad_2d))
epoch 20, x1: -0.002295, x2: -0.000000
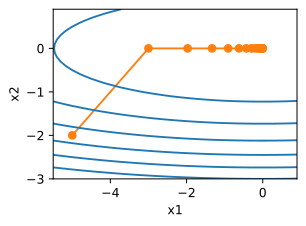
可以看出,在越接近最优点附近,学习率越来越小,参数更新变得更慢,以至于不会错过最优点的位置。
下面看看在Pytorch中如何使用
AdaGrad
优化算法,在Pytorch中的格式为:
torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0, eps=1e-10)
各个参数的功能为:
params– 要优化的参数。lr(float, optional) – 学习率 (默认: 1e-2)lr_decay(float, optional) – 学习率衰减 (默认: 0)weight_decay(float, optional) – 权重衰减 (L2 penalty) (默认: 0)eps(float, optional) – 为提高数字稳定性,在分母上添加了该项 (默认: 1e-10)
3.4、RMSProp算法
RMSProp算法通过修改AdaGrad得来,其目的是在非凸背景下效果更好。针对梯度平方和累计越来越大的问题,RMSProp指数加权的移动平均代替梯度平方和。RMSProp为了使用移动平均,还引入了一个新的超参数
ρ
\rho
ρ,用来控制移动平均的长度范围。以下是RMSProp算法的更新步骤:
更
新
梯
度
:
g
^
←
1
b
a
t
c
h
_
s
i
z
e
∑
i
=
0
b
a
t
c
h
_
s
i
z
e
∇
θ
L
(
f
(
x
(
i
)
)
,
y
(
i
)
)
累
积
平
方
梯
度
:
r
←
ρ
r
+
(
1
−
ρ
)
g
^
⊙
g
^
计
算
参
数
更
新
:
△
θ
←
−
λ
δ
+
r
⊙
g
^
更
新
参
数
:
θ
←
θ
+
△
θ
更新梯度:\hat{g} \leftarrow \frac{1}{batch\_size} \sum_{i=0}^{batch\_size}\nabla_{\theta}L(f(x^{(i)}),y^{(i)})\\ 累积平方梯度:r \leftarrow \rho r+ (1- \rho) \hat{g} \odot \hat{g}\\ 计算参数更新:\triangle \theta \leftarrow - \frac{\lambda}{\delta+\sqrt{r}}\odot \hat{g}\\ 更新参数:\theta \leftarrow \theta+\triangle \theta
更新梯度:g^←batch_size1i=0∑batch_size∇θL(f(x(i)),y(i))累积平方梯度:r←ρr+(1−ρ)g^⊙g^计算参数更新:△θ←−δ+rλ⊙g^更新参数:θ←θ+△θ
RMSProp算法在实践中已被证明是一种有效且实用的深度神经网络优化算法,因而在深度学习中得到了广泛应用。
和之前一样,使用二次函数
f
(
x
)
=
0.1
x
1
2
+
2
x
2
2
f(x)=0.1x_1^2+2x_2^2
f(x)=0.1x12+2x22来观察RMSProp的轨迹。在使用学习率为0.4的
AdaGrad
的时候,参数在算法的后期阶段移动的越来越慢,因为学习率下降太快。由于
η
\eta
η是单独控制的,
RMSProp
不会发生这种情况。
import math
from d2l import torch as d2l
#rmsprop更新参数defrmsprop_2d(x1,x2,s1,s2):
g1,g2,eps=0.2*x1,4*x2,1e-6
s1=gamma*s1+(1-gamma)*g1**2
s2=gamma*s2+(1-gamma)*g2**2
x1-=eta/math.sqrt(s1+eps)*g1
x2-=eta/math.sqrt(s2+eps)*g2
return x1,x2,s1,s2
#目标函数deff_2d(x1,x2):return0.1*x1**2+2*x2**2
eta,gamma=0.4,0.9
d2l.show_trace_2d(f_2d,d2l.train_2d(rmsprop_2d))
epoch 20, x1: -0.010599, x2: 0.000000
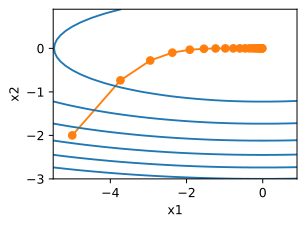
在pytorch中,RMSProp算法的格式为:
torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)
alpha
为平滑常数,
momentum
为动量。
3.5、Adam算法
Adam本质上是带有动量项的RMSProp,它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围,使参数比较稳定。
Adam是一种学习速率自适应的深度神经网络方法,他利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam算法的更新步骤如下:
t
←
t
+
1
计
算
梯
度
:
g
t
←
∇
θ
f
t
(
θ
t
−
1
)
更
新
有
偏
一
阶
矩
估
计
:
m
t
←
β
1
⋅
m
t
−
1
+
(
1
−
β
1
)
⋅
g
t
更
新
有
偏
二
阶
矩
估
计
:
v
t
←
β
2
⋅
v
t
−
1
+
(
1
−
β
2
)
⋅
g
t
2
计
算
偏
差
校
正
的
一
阶
矩
估
计
:
m
t
^
←
m
t
1
−
β
1
t
计
算
偏
差
校
正
的
二
阶
矩
估
计
:
v
t
^
←
v
t
1
−
β
2
t
更
新
参
数
:
θ
t
←
θ
t
−
1
−
α
⋅
m
t
^
ϵ
+
v
t
^
t \leftarrow t+1\\ 计算梯度:g_t \leftarrow \nabla_{\theta} f_t(\theta_{t-1})\\ 更新有偏一阶矩估计:m_t \leftarrow \beta_1 \cdot m_{t-1} + (1-\beta_1)\cdot g_t\\ 更新有偏二阶矩估计:v_t \leftarrow \beta_2 \cdot v_{t-1} + (1-\beta_2)\cdot g_t^2\\ 计算偏差校正的一阶矩估计:\hat{m_t} \leftarrow \frac{m_t}{1-\beta_1^t}\\ 计算偏差校正的二阶矩估计:\hat{v_t} \leftarrow \frac{v_t}{1-\beta_2^t}\\ 更新参数:\theta_t \leftarrow \theta_{t-1}-\alpha \cdot \frac{\hat{m_t}}{\epsilon+\sqrt{\hat{v_t}}}
t←t+1计算梯度:gt←∇θft(θt−1)更新有偏一阶矩估计:mt←β1⋅mt−1+(1−β1)⋅gt更新有偏二阶矩估计:vt←β2⋅vt−1+(1−β2)⋅gt2计算偏差校正的一阶矩估计:mt^←1−β1tmt计算偏差校正的二阶矩估计:vt^←1−β2tvt更新参数:θt←θt−1−α⋅ϵ+vt^mt^
下面看看每个步骤的含义是:
首先,计算梯度的指数移动平均数,
m
0
m_0
m0初始化为0。类似于Momentum算法,综合考虑之前时间步的梯度动量。
β
1
\beta_1
β1系数为指数衰减率,控制权重分配(动量与当前梯度),通常取接近于1的值。默认为0.9
m
t
←
β
1
⋅
m
t
−
1
+
(
1
−
β
1
)
⋅
g
t
m_t \leftarrow \beta_1 \cdot m_{t-1} + (1-\beta_1)\cdot g_t
mt←β1⋅mt−1+(1−β1)⋅gt
其次,计算梯度平方的指数移动平均数,
v
0
v_0
v0初始化为0。
β
2
\beta_2
β2系数为指数衰减率,控制之前的梯度平方的影响情况。类似于RMSProp算法,对梯度平方进行加权均值。默认为0.999
v
t
←
β
2
⋅
v
t
−
1
+
(
1
−
β
2
)
⋅
g
t
2
v_t \leftarrow \beta_2 \cdot v_{t-1} + (1-\beta_2)\cdot g_t^2
vt←β2⋅vt−1+(1−β2)⋅gt2
第三,由于
m
0
m_0
m0初始化为0,会导致
m
t
m_t
mt偏向于0,尤其在训练初期阶段。所以,此处需要对梯度均值
m
t
m_t
mt进行偏差纠正,降低偏差对训练初期的影响。
m
t
^
←
m
t
1
−
β
1
t
\hat{m_t} \leftarrow \frac{m_t}{1-\beta_1^t}
mt^←1−β1tmt
第四,与
m
0
m_0
m0类似,因为
v
0
v_0
v0初始化为0导致训练初始阶段
v
t
v_t
vt偏向0,对其进行纠正。
v
t
^
←
v
t
1
−
β
2
t
\hat{v_t} \leftarrow \frac{v_t}{1-\beta_2^t}
vt^←1−β2tvt
最后,更新参数,初始的学习率
α
\alpha
α乘以梯度均值与梯度方差的平方根之比。其中默认学习率
α
=
0.001
\alpha=0.001
α=0.001,
ϵ
=
1
0
−
8
\epsilon=10^{-8}
ϵ=10−8,避免除数变为0。由表达式可以看出,对更新的步长计算,能够从梯度均值及梯度平方两个角度进行自适应地调节,而不是直接由当前梯度决定。
θ
t
←
θ
t
−
1
−
α
⋅
m
t
^
ϵ
+
v
t
^
\theta_t \leftarrow \theta_{t-1}-\alpha \cdot \frac{\hat{m_t}}{\epsilon+\sqrt{\hat{v_t}}}
θt←θt−1−α⋅ϵ+vt^mt^
Adam主要包含以下几个显著的优点:
- 实现简单,计算高效,对内存需求少
- 参数的更新不受梯度的伸缩变换影响
- 超参数具有很好的解释性,且通常无需调整或仅需很少的微调
- 更新的步长能够被限制在大致的范围内(初始学习率)
- 能自然地实现步长退火过程(自动调整学习率)
- 很适合应用于大规模的数据及参数的场景
- 适用于不稳定目标函数
- 适用于梯度稀疏或梯度存在很大噪声的问题
和之前一样,使用二次函数 𝑓(𝑥)=0.1𝑥21+2𝑥22 来观察Adam的轨迹。使用学习率为0.16的AdaGrad并迭代50次。
import math
from d2l import torch as d2l
%matplotlib inline
#针对Adam改造原来的优化目标函数deftrain_2d_adam(trainer,steps=20,f_grad=None):
x1,x2,m1,m2,v1,v2=-5,-2,0,0,0,0
results=[(x1,x2)]for i inrange(steps):
x1,x2,m1,m2,v1,v2=trainer(x1,x2,m1,m2,v1,v2)
results.append((x1,x2))print(f'epoch{i+1},x1:{float(x1):f},x2:{float(x2):f}')return results
#Adam更新参数过程defrmsprop_2d(x1,x2,m1,m2,v1,v2):
g1,g2,eps=0.2*x1,4*x2,1e-8
m1=beta1*m1+(1-beta1)*g1
m2=beta1*m2+(1-beta1)*g2
v1=beta2*v1+(1-beta2)*g1**2
v2=beta2*v2+(1-beta2)*g2**2
m_hat_1=m1/(1-beta1)
m_hat_2=m2/(1-beta1)
v_hat_1=v1/(1-beta2)
v_hat_2=v2/(1-beta2)
x1-=alpha*(m_hat_1/(eps+math.sqrt(v_hat_1)))
x2-=alpha*(m_hat_2/(eps+math.sqrt(v_hat_2)))return x1,x2,m1,m2,v1,v2
#目标函数deff_2d(x1,x2):return0.1*x1**2+2*x2**2
alpha,beta1,beta2=0.16,0.9,0.999
d2l.show_trace_2d(f_2d,train_2d_adam(rmsprop_2d))
epoch20,x1:0.131652,x2:0.447787
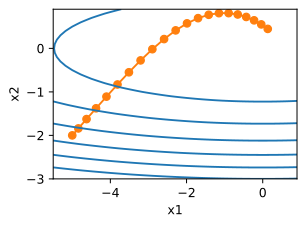
在pytorch中Adam的使用格式为
torch.optim.Adam(params, lr=0.001, betas=(0.9,0.999), eps=1e-08, weight_decay=0, amsgrad=False,*, maximize=False)
参数
betas
为
β
1
\beta_1
β1和
β
2
\beta_2
β2的集合,分别控制权重分配和之前的梯度平方的影响情况。
版权归原作者 CityD 所有, 如有侵权,请联系我们删除。