点关注不迷路,欢迎推荐给更多人
1 技巧
1.1 取消同步(节约时间,甚至能多骗点分,最好每个程序都写上)
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
1.2 万能库(可能会耽误编译时间,但是省脑子)
#include <bits/stdc++.h>
1.3 蓝桥杯return 0千万别忘了写!!
1.4 编译设置(Dev C++)
(1)工具->编译选项->编译器->编译时加入以下命令->调成C99
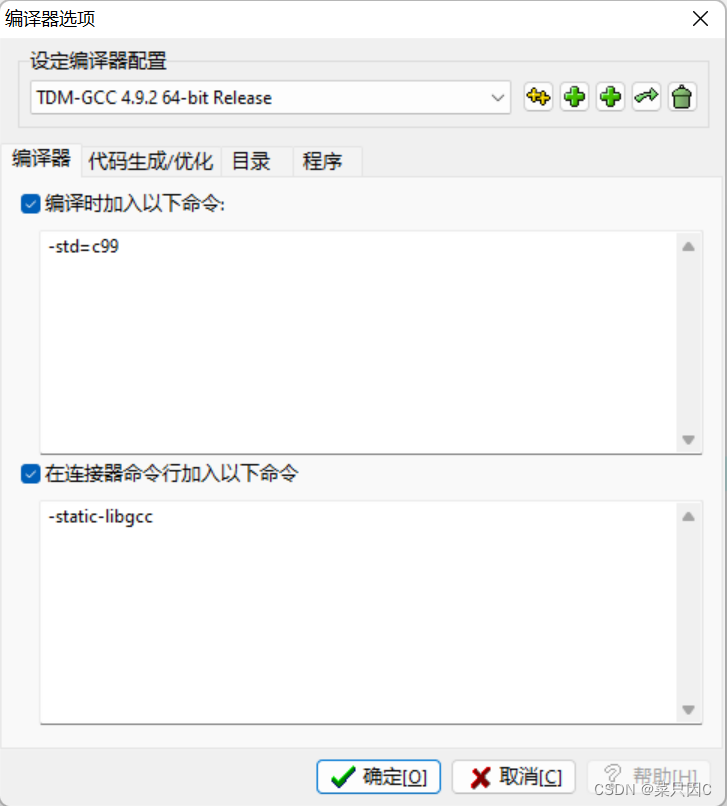
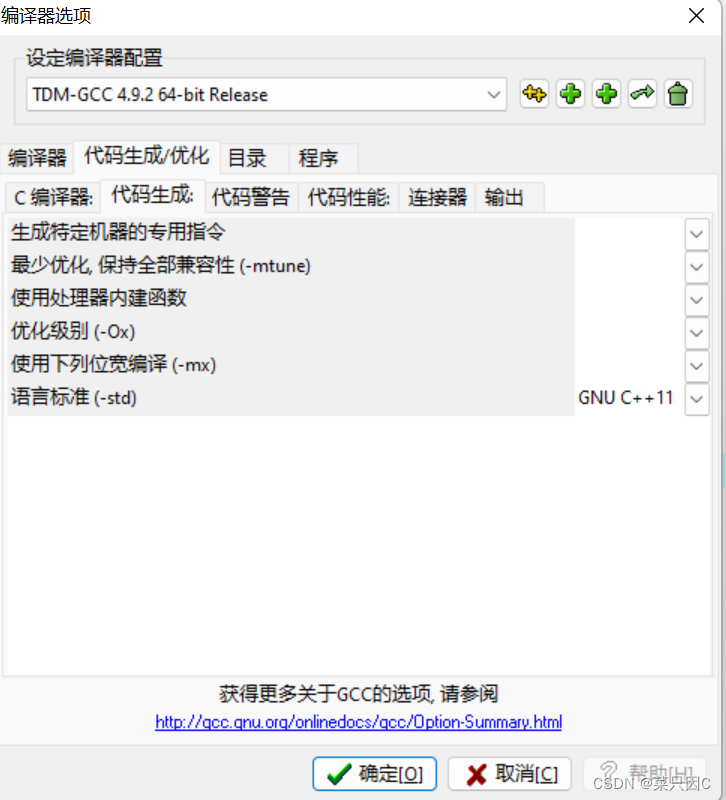
(2)工具->编译选项->代码生成/优化->代码生成->语言标准
1.5 memset填充函数
按照字节对内存块进行初始化,注意只能填充0或-1
#include <bits/stdc++.h>
using namespace std;
int a[10];
int main()
{
memset(a,-1,sizeof(a));
for(int i=0;i<10;i++)
{
cout<<a[i]<<endl;
}
return 0;
}
1.6 时间复杂度
蓝桥杯每一道题编译时间都限制在1s以内,遇到数据比较大的题目,往往需要降低时间复杂度。
粗略估计,O(n)情况下一秒大概完成4亿次,O(nn)情况下一秒大概完成2万次,O(nn*n)情况下大概完成700次。
由于蓝桥杯评测系统是根据通过样例数来评分,所以我们做题时一定要注意约定样例取值范围。
例题:K倍区间(暴力法只能通过部分样例,所以要用更好的算法)
(1条消息) K倍区间(蓝桥杯2017年第八届省赛B组第十题)(C/C++)_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128434135?spm=1001.2014.3001.5501
1.6.1 常数阶 O(1)
int i=1;
int j=2;
int m=i+j;
1.6.2 对数阶 O(logn)
int i=1;
while(i<n)
{
i=i*2;
}
1.6.3 线性阶 O(n)
for(int i=0;i<n;i++)
{
cout<<i<<endl;
)
1.6.4 线性对数阶 O(nlogn)
for(int m=1;m<n;m++)
{
int i=1;
while(i<n)
{
i=i*2;
}
}
1.6.5 多重循环 O(n^k)
k为循环层数
1.7 剪枝
做题时已经发现的不可能取到的数值,就不要再让计算机算了,尽量节省时间,蓝桥杯中目前遇到的还没有用到过过于繁琐的剪枝,大多也是在BFS和DFS中出现(bool vis)
1.8 find函数
函数作用:查找该元素在数组中第一次出现的位置的地址(类似于0x的地址)
模型:find(查找起点,查找终点,查找目标元素)
同样,查找区间为[查找起点,查找终点)
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a[10]={2,6,8,1,3,7,5,1,0,11};
cout<<find(a+0,a+5,8)<<endl;//打印类似0x地址
cout<<find(a+0,a+5,8)-a<<endl;//打印数组【】内的序号
return 0;
}
1.9 PI问题
PI=atan(1.0)*4
2 基本算法及技巧
2.1 BFS(宽度优先搜索)
用到队列(有时会用到优先队列)
主要思想:把所有符合条件的点都压入队列,然后挨个元素弹出上下左右前后搜索,直到队列清空时代表搜索完毕,搜索的时候注意判断是否已经搜索过,用bool vis【】判断。
例题:全球变暖
(1条消息) 全球变暖(蓝桥杯2018年省赛B组试题I)(C/C++)_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128434254?spm=1001.2014.3001.5502
2.2 DFS(深度优先搜索)
用到递归(不好理解)
主要模板:可参见如下全排列例题
总结起来有如下几步:
(1)确定 边界 if()return;
(2)进入for循环
(3)判断是否搜索过 if(vis[])vis[]=true; dfs(); vis[]=false;
例题:凑算式
(3条消息) 凑算式(蓝桥杯2016年省赛B组第三题)(C/C++)_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128434004?spm=1001.2014.3001.5502
2.3 最大公约数和最小公倍数
最大公约数(greatest common divisor,gcd)
#include <bits/stdc++.h>
using namespace std;
int main()
{
cout<<__gcd(25,5);
return 0;
}
最小公倍数 (least common multiple,lcm)
多写一个lcm函数
#include <bits/stdc++.h>
using namespace std;
int lcm(int a,int b)
{
return a*b/__gcd(a,b);
}
int main()
{
cout<<lcm(25,5);
return 0;
}
2.4 进制转换
2.4.1 十进制为媒介(常用型)
(8条消息) 任意进制转换成十进制/十进制转换成任意进制(ASCII码法)(C/C++)_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128297645?spm=1001.2014.3001.5502
2.4.2 二进制为媒介(技巧型)
(2条消息) 十六进制转八进制(蓝桥杯基础练习C/C++)_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128745875?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22128745875%22%2C%22source%22%3A%22m0_71934846%22%7D
2.5 二进制表示法
例题:无聊的逗
(8条消息) 蓝桥杯试题 算法训练 无聊的逗(C/C++)_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128717938?spm=1001.2014.3001.5502
2.6 背包问题
2.6.1 01背包问题
#include<bits/stdc++.h>
using namespace std;
int v[1000]; // 体积
int w[1000]; // 价值
int f[1000][1000]; // f[i][j], j体积下前i个物品的最大价值
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
{
// 当前背包容量装不进第i个物品,则价值等于前i-1个物品
if(j < v[i])
f[i][j] = f[i - 1][j];
// 能装,需进行决策是否选择第i个物品
else
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
2.6.2 多重背包问题(每种物品有多件)
把多件物品捏合成一件新的物品,按序号往后叠加即可
2.6.3 完全背包问题(每种物品有无数件)
#include<iostream>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i = 1 ; i <= n ;i ++)
{
cin>>v[i]>>w[i];
}
for(int i = 1 ; i<=n ;i++)
for(int j = v[i] ; j<=m ;j++)
{
f[j] = max(f[j],f[j-v[i]]+w[i]);
}
cout<<f[m]<<endl;
}
2.7 动态规划(DP)
例题:拿金币
(1条消息) 拿金币(蓝桥杯算法训练)(C/C++)_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128456365?spm=1001.2014.3001.5502
2.8 贪心
思路:选取局部最优解,但是最大的缺陷就是在某些情况下不适用
举例:纸币问题
比如面额有1元,2元,5元,10元,20元,50元,100元,那么对于110元来说,可以用贪心从最大面额100元开始找。
但是如果改纸币面额,比如1元,2元,5元,20元,55元,100元,那么如果用到贪心算法,会发现并不能找出最优解(贪心:100+5+5=110 动态规划:55+55=110)
2.9 分治(以后更新)
大部分是二分法
2.10 数字分拆到数组中
(2条消息) 把一个数字分拆存到数组内(C/C++)_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128698111?spm=1001.2014.3001.5501
2.11 数字和字符串的互化
求不了子数字,但能求子字符串
例题:超级质数
(2条消息) 超级质数(蓝桥杯C/C++算法赛)_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128723978?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22128723978%22%2C%22source%22%3A%22m0_71934846%22%7D
2.12 排序
(4条消息) 找字符串中最大字符(三种快速方法)_求字符串中最大的字符_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128457227?spm=1001.2014.3001.5501
3 STL
3.1 队列(queue)

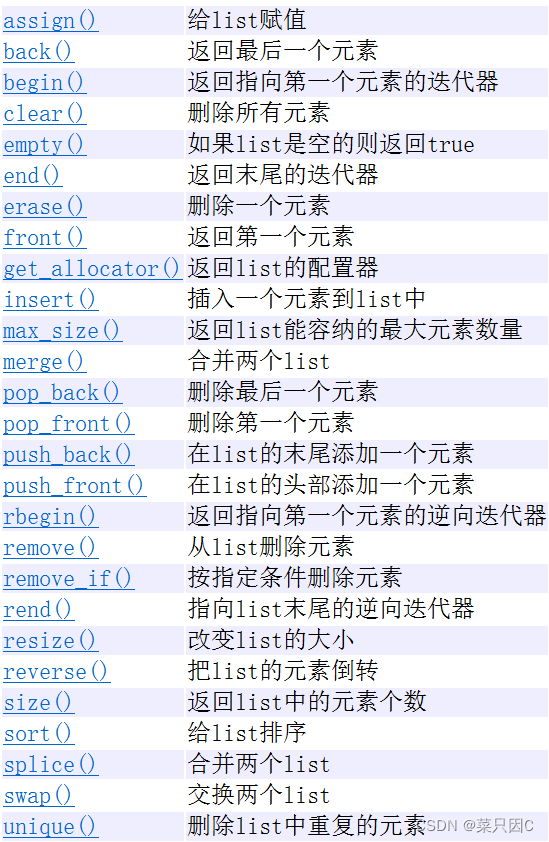
3.2 链表(list)
3.3 优先队列(priority queue)

优先队列默认大根堆(大到小排序),如果想从小到大排序,那么
<int,vector<int>,greater<int> >//升序排列(小根堆)
<int,vector<int>,less<int> >//降序排列(大根堆)
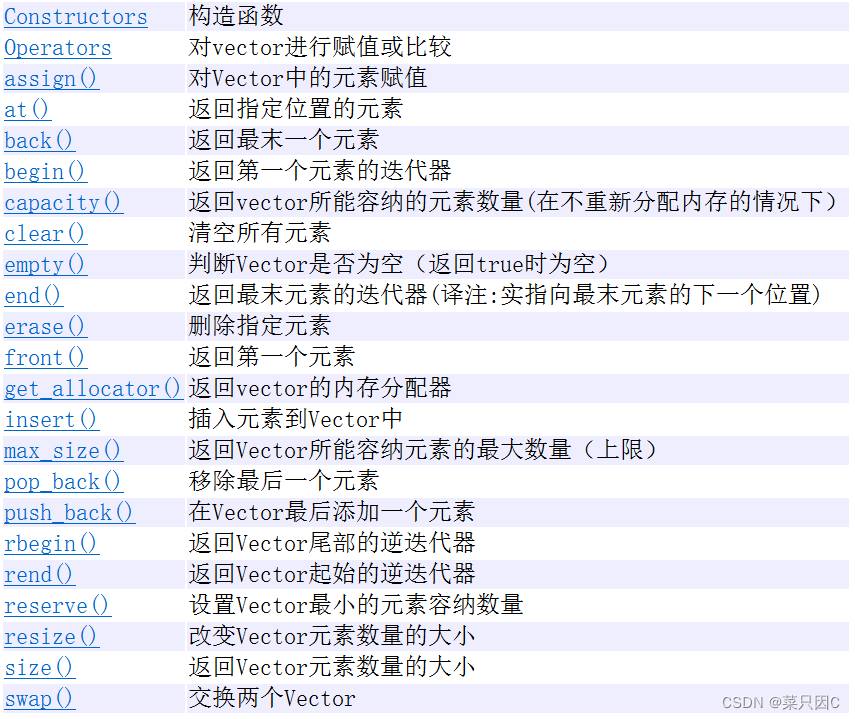
3.4 向量/动态数组(vector)
3.5 栈(stack)

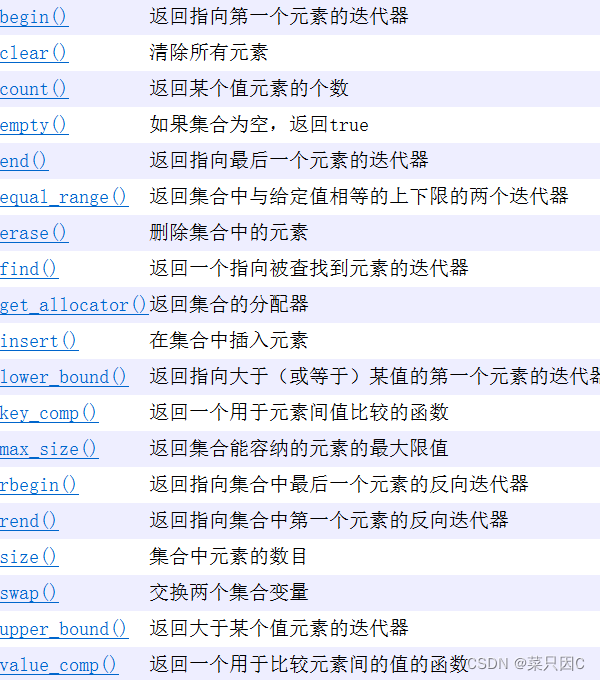
3.6 集合(set) (要求没有重复元素)
set<int> s;//默认升序排列
set<int, greater<int>> s2 = {3,2,5,1,4 ,3};//降序
set值不能修改(修改过后无法保证数据顺序)
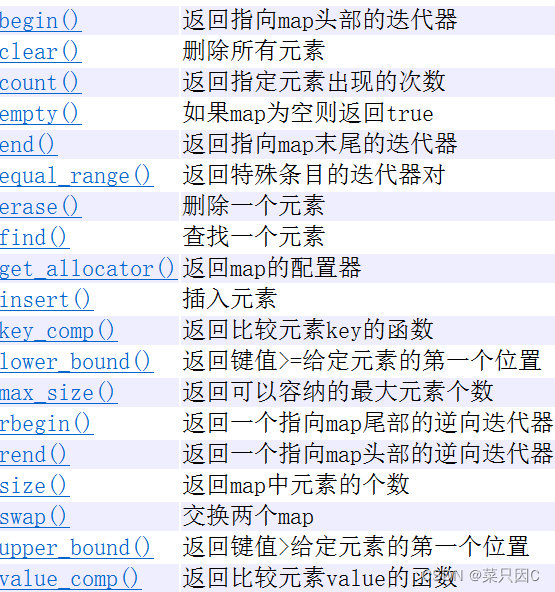
3.7 集合/映射/键值对(map)

3.8 迭代器

模板:
#include<iostream>
#include<vector>
using namespace std;
int main()
{
vector<int> v;
v.push_back(11);
v.push_back(7);
vector<int>::iterator it = v.begin();
while(it!=v.end())
{
cout << *it <<" ";
it++;
}
cout << endl;
return 0;
}
这里大概列出参加蓝桥杯需要掌握的知识点和技巧,若想详细了解某个知识点,可以看看我的例题和别人的文章
版权归原作者 菜只因C 所有, 如有侵权,请联系我们删除。