【蓝桥真题3】蓝桥改革变难，想进国赛这些能力你可缺一不可

⭐️引言⭐️

           大家好，我是执梗。蓝桥杯省赛的倒计时也就剩下一个月的时间了，如果练过近七八年的真题的小伙伴，很明显地能感觉到蓝桥杯的难度越来越大，虽然遥遥还比不上ACM，但它的平均难度正以明显地速度增加。对于这样的变化，不知道大家是否熟练掌握了一些对于蓝桥杯特别中意且高频的考点呢？一些必须掌握的能力又是否熟练掌握了呢？下面我来为大家总结一下。

⭐️往期集锦⭐️
蓝桥真题1【蓝桥真题1】这道用了7个for循环的蓝桥真题，让舍友哭着跑出考场【内附原题资源】蓝桥真题2【蓝桥真题2】蓝桥杯不会全排列，那就只能写10个for循环了【内附近8年真题资源】

🍋1.快速求最大公约数及最大公倍数

    这个考点我相信大家一定不陌生，求最大公约数有的人可能还用的是遍历去查询，如果是填空题时间长点可能无所谓，但是如果大题涉及到最大公约数或者公倍数的问题，蓝桥杯的数据量是出名的大（这个后面会体现），超时是肯定的。所以请大家背下欧几里得公式直接使用（已知效率最快求出公倍数地公式）

   ** 1.gcd函数（欧几里得算法原理）**

//返回值则是a和b的最大公约数
int gcd(int a,int b){
        return b == 0 ? a:gcd(b,a%b);
}

    **2.lcm函数（速求最大公倍数，原理基于gcd函数）**

//返回值为a和b的最大公倍数
int lcm(int a, int b){
    return a/gcd(a,b)*b;//最小公倍数=两数之积÷两数最大公约数    
}

☀️1.1既约分数

如果一个分数的分子和分母的最大公约数是 1，这个分数称为既约分数。

例如，3/4，1/8，7/1 都是既约分数。

请问，有多少个既约分数，分子和分母都是 1 到 2020 之间的整数（包括 1和 2020）？

题目链接：既约分数

    这道题是一道填空题，在真实的考试环境下我们即使使用朴素求最大公约数的方法仍然可以抛出答案，但在蓝桥官方的oi平台是会超时的，根据题意利用欧几里得公式可以直接写出代码。

import java.util.Scanner;
public class Main {
    static int ans=0;
    public static void main(String[] args) {
        for(int i=1;i<=2020;i++){
          for(int j=1;j<=2020;j++){
            if((gcd(i,j)==1)) ans++;
          }
        }
        System.out.println(ans);//答案为2481215
    }
     static int gcd(int a,int b){
       return b == 0 ? a:gcd(b,a%b);
     }
}

🌁 1.2分数

1/1​+1/2​+1/4​+1/8+⋯

每项是前一项的一半，如果一共有 20 项,求这个和是多少，结果用分数表示出来。

类似：3/2，当然，这只是加了前 2 项而已。分子分母要求互质。

题目链接：分数

      这道题比较简单，我们求出分子和分母即可。不过题目要求互质，所以我们可以应用gcd函数求出分子和分母的最大公约数进行约分。                

public class 分数 {
    public static void main(String[] args) {
        //x为分母
        int x=1;
        //count为分子
        int count=1;
        for(int i=2;i<=20;i++) {
            x*=2;
            count+=x;
        }
        //打印一下分子分母看看
        System.out.println(x);//524288
        System.out.println(count);//1048575
        int a=gcd(x,count);//最大公约数发现就为1
        int b=x/a;
        int d=count/a;
        //打印答案
        System.out.println(d+"/"+b);//1048575/524288
    }
    static int gcd(int a,int b) {
        return b==0?a:gcd(b,a%b);
    }
}

🍋2.对于日期的处理能力（重点）

    考察日期的处理，这几乎是蓝桥杯每届必考的考点。这一点我在前面的蓝桥真题中也提起过，大家可以通过上面的链接去看。Java组的同学必须学会使用Calendar这个函数，它能快速求出某年某月某日是星期几，这对于繁杂的日期处理题来说，简直是神器。

☔️2.1世纪末的星期

    题目：有邪教称1999年12月31日是世界末日，当然谣言已经不攻自破。还有人称今后的某个世纪末的12月31日，如果是星期一则会....有趣的是，任何一个世纪末的年份的12月31日都不可能是星期一！！！于是"谣言制造商"又修改为星期日.......

    1999年12月31日是星期五，请问：未来哪一个离我们最近的一个世纪末年(即XX99年)的12月31日正好是星期天（即星期日）？ 回答年份即可       

       这是一道很久远的一道蓝桥真题（还是第一题），按道理蓝桥杯的第一题都是一眼能得出答案的，但是这道题按照常规的方法来处理还是有点麻烦的。但通过Calendar却可以秒杀这道题。

public class 世纪末的星期 {
    public static void main(String[] args) {
        //注意Calendar实例的获取方式
        Calendar calendar = Calendar.getInstance();
        for (int year = 1999; year <10000 ; year+=100) {
            //设置年月日
            calendar.set(Calendar.YEAR,year);
            calendar.set(Calendar.MONTH,11);//其实是12月
            calendar.set(Calendar.DAY_OF_MONTH,31);
            //判断是星期几
            if (calendar.get(Calendar.DAY_OF_WEEK)==1) {
            //sunday是第一天，所以为1时是Sunday,通过源码查看
                System.out.println(year);// 2299
                break;
            }
        }
    }
}

☁️2.2跑步锻炼

小蓝每天都锻炼身体。

正常情况下，小蓝每天跑 1 千米。如果某天是周一或者月初（11日），为了激励自己，小蓝要跑 2 千米。如果同时是周一或月初，小蓝也是跑 2 千米。

小蓝跑步已经坚持了很长时间，从 2000 年 11 月 11 日周六（含）到 2020 年 10 月 1 日周四（含）。请问这段时间小蓝总共跑步多少千米？

题目链接：跑步锻炼

       这道题目需要我们去进行日期的模拟，用一个数组去表示每个月的日子，对于闰年的二月去进行特判。

public class 跑步锻炼 {
    static int[] M={0,31,28,31,30,31,30,31,31,30,31,30,31};
    public static void main(String[] args) {
        int y = 2000, m = 1, d = 1, w = 6, ans = 0;
        while(y!=2020 || m!=10 || d!=1){
            if(y%400==0 || (y%4==0&&y%100!=0)){
                M[2] = 29;
            }
            else{
                M[2] = 28; //M是全局变量
            }
            d++;
            w = (w + 1) % 7;//w为0为星期天
            if(d > M[m]){
                d = 1;
                m ++; 
            } 
            if(m>12){
                m = 1;
                y ++;
            } 
            if(d==1 || w==1){
                ans++;  //是月初或者周一多加一次 
            }
            ans++;
        }
        //这个循环是先加值再加日期，所以2020.1.10号的已经加上去了，但是2000.1.1没加上，所以加2
        ans+=2;
        System.out.println(ans);//8879
    }
}

❄️2.3星期一

整个 2020 世纪（1901 年 1 月 1 日至 2000 年 12 月 31 日之间），一共有多少个星期一？

题目链接：星期一

        同样是日期模拟的问题，需要去判断星期一的个数。这道题我的思路是结合上面两道日期题的做法。先利用Calendar算出起始日期和结尾日期是星期几。再利用跑步锻炼题目的模板结合模拟。可以算出答案为5217。

      **为什么要知道起始是星期几？**

** 因为这个代码模板需要知道起始的日期，而最后一天2000年12月31日是没有在循环中判断的。我们需要特判一下，当然我们也可以让循环在2001年1月1日结束，这样不需要特判。**

public class 星期一 {
    static int[] M={0,31,28,31,30,31,30,31,31,30,31,30,31};
    public static void main(String[] args) {
        Calendar c=Calendar.getInstance();
        c.set(Calendar.YEAR, 1901);
        c.set(Calendar.MONTH, 0);
        c.set(Calendar.DAY_OF_MONTH, 1);
        System.out.println(c.get(Calendar.DAY_OF_WEEK));//3所以为星期二 
        Calendar c2=Calendar.getInstance();
        c2.set(Calendar.YEAR, 2000);
        c2.set(Calendar.MONTH, 11);
        c2.set(Calendar.DAY_OF_MONTH, 31);
        System.out.println(c2.get(Calendar.DAY_OF_WEEK));//1 所以是星期天
        test();
    }    
     static void test() {
        int y = 1901, m = 1, d = 1, w = 2, ans = 0;
        while(y!=2000 || m!=12 || d!=31){
            if(y%400==0 || (y%4==0&&y%100!=0)){
                M[2] = 29;
            }
            else{
                M[2] = 28; //这个必须加，因为M为全局变量 
            }
            d++;
            w = (w + 1) % 7;//w为0为星期天
            if(d > M[m]){
                d = 1;
                m ++; 
            } 
            if(m>12){
                m = 1;
                y ++;
            } 
            if(w==1){
                ans++;  //是周一就加
            }
        }
        //我们已经知道2000.12.31不是星期1,不需要特判
        System.out.println(ans);//5217
    }
}

⛄️2.4猜生日

今年的植树节（2012 年 3 月 12 日），小明和他的叔叔还有小伙伴们一起去植树。休息的时候，小明的同学问他叔叔多大年纪，他叔叔说：“我说个题目，看你们谁先猜出来！”

“把我出生的年月日连起来拼成一个 8位数（月、日不足两位前补 0）正好可以被今天的年、月、日整除！”

他想了想，又补充到：“再给个提示，我是 6 月出生的。”

根据这些信息，请你帮小明算一下，他叔叔的出生年月日。

格式是年月日连成的 88 位数。例如，如果是 1948 年 6 月 12 日，就写：19480612。

题目链接：猜生日

      这道题表面上考的和日期有关，但已经告诉了我们月份了，难度大大降低，根本不用去考虑闰年平年有关二月份的问题，考的只是普通的模拟而已。

public class 猜生日 {
    static int a=2012;
    static int b=3;
    static int c=12;
    public static void main(String[] args) {
        for(int i=1900;i<2000;i++){
           for(int j=1;j<=30;j++){             
                long count=i*10000+600+j;
                //同时是年月份的倍数则是答案
                if(count%2012==0&&count%3==0&&count%12==0){
                  System.out.println(count);//19550604
                }           
           }
        }
    }
}

🍋3.超大数据处理问题

     这也是蓝桥杯的一大特色，无论是填空题还是大题，数据范围都大的离谱。填空题用int必爆，大题用int拿不到满分。所以对于大数据的处理问题，是非常重要的一项能力，通过真题我们来看看就找到了

⚡️3.1棋盘放麦子

你一定听说过这个故事。国王对发明国际象棋的大臣很佩服，问他要什么报酬，大臣说：请在第 1个棋盘格放 1 粒麦子，在第 2 个棋盘格放 2 粒麦子，在第 3 个棋盘格放 4 粒麦子，在第 4 个棋盘格放 8 粒麦子，......后一格的数字是前一格的两倍，直到放完所有棋盘格（国际象棋共有 64 格）。

国王以为他只是想要一袋麦子而已，哈哈大笑。

当时的条件下无法准确计算，但估算结果令人吃惊：即使全世界都铺满麦子也不够用！

请你借助计算机准确地计算，到底需要多少粒麦子。

题目链接：棋盘放麦子

   题目都说全世界都铺满麦子都不敢用，那我们可想而知这个数是有多大！int肯定是不行，用long去计算肯定也是同样的结果——会爆掉！这时候理所当然地去想究竟还能不能表示出比long更大地值？既然题目这样问了，那肯定是有的，那就是——**BigInteegr。**这个类相信很多人都没有用过，因为确实大部分的题目long已经够用了。这个类比较麻烦，因为加减乘除都需要通过方法去完成，这里大家可以去查API文档使用它。**大家可以看看这个数究竟有多大！**

public class 棋盘放麦子 {
    public static void main(String[] args) {
        BigInteger count=new BigInteger("1");
        BigInteger ans=new BigInteger("1");
        BigInteger x=new BigInteger("2");
        for(int i=2;i<=64;i++){
            ans=ans.multiply(x);
            count=count.add(ans);
        }
        System.out.println(count);//18446744073709551615
    }
}

🌀3.2数列求值

给定数列 1, 1, 1, 3, 5, 9, 17,……从第 4 项开始，每项都是前 3 项的和。

求第 20190324 项的最后 4 位数字。

题目链接：数列求值

       这道题的目的并不是要让大家去用什么大数据类型处理，要去分析题意！这个数之大肯定是无法用数字表示的，而题目只要求我们最后4位数字——更加说明所以这道题根本不需要去大数据处理！题目只关心最后四位数字，而前面的数字根部不会影响后面的数字，所以当我们的数字大于4位数时，我们只保留它的后四位即可。

public class 数列求值 {
     public static void main(String[] args) {
            int a=1;
            int b=1;
            int c=1;
            int d =0;
            for(int i=4;i<=20190324;i++){
              d=a+b+c;
              if(d>10000) d=check(d);
              a=b;
              b=c;
              c=d;
            }
            System.out.println(d);//4659
        }
        static int check(int n){
          return n%10000;
        }
}

🍏 4.打表模拟能力

    之所以说打表能力是重中之重，是因为掌握好它，不仅能快速算出答案节省出我们很多的时间，对于许多题目还能化繁为简。之所以能如此，是因为蓝桥的填空题只需要答案，哪怕你写的程序要跑个几分钟才能跑出答案，那有如何？只要我的答案是对的，而且一般打表最多也就十几秒钟，**想要进国赛？不会打表那可不行！**光说不练肯定无用！直接上题

🌊4.1算式问题

看这个算式：

☆☆☆ + ☆☆☆ = ☆☆☆

如果每个五角星代表 11 ~ 99 的不同的数字。

这个算式有多少种可能的正确填写方法？

题目链接：算式问题

     这道题很简单，考的就是全排列，全排列的重要性不言而喻，在算法真题1中我出了各种详细真题，还不会的小伙伴们一定要掌握！首先给出模板全排列做法。**test方法是固定全排列模板方法，check的逻辑根据题目要求来写。**

public class 算式问题 {
    static int[] arr= {1,2,3,4,5,6,7,8,9};
    static int ans=0;
    public static void main(String[] args) {
        test(0);
        System.out.println(ans);//336
    }
    static void test(int k) {
        if(k==9) {
            if(check()) ans++;
            return;
        }
        for(int i=k;i<arr.length;i++) {
            exch(k,i);
            test(k+1);
            exch(k,i);
        }
    }    
    static boolean check() {
        int a=arr[0]*100+arr[1]*10+arr[2];
        int b=arr[3]*100+arr[4]*10+arr[5];
        int c=arr[6]*100+arr[7]*10+arr[8];
        return a+b==c;
    }
    static void exch(int a,int b) {
        int tmp=arr[a];
        arr[a]=arr[b];
        arr[b]=tmp;
    }
}

    有的兄弟说，万一全排列没记住咋办？？没办法了，那只能打表了，去模拟所有的三位数加法情况，再去判断是否满足九个数不相等。代码量还是有点大，但是考场上做不出来也只能如此了。

    **我们把A从123到987进行模拟，因为123是满足题目要求的最小数字，987是满足题目要求的最大数字，则B应该对于为（123到987）-A。然后A+B得到一个C，再去判断是否满足九个数不相等。**

import java.util.Map;
import java.util.Scanner;
import java.util.TreeMap;

public class Main {

    static int check(int a, int b, int c)
    {
        int flag[]=new int[11];
        for(int i=0;i<10;i++) flag[i]=0;
        flag[0]=1;
        while(a!=0)
        {
            if(flag[a%10]==1) return 0;
            else flag[a%10]=1;

            if(flag[b%10]==1) return 0;
            else flag[b%10]=1  ;

            if(flag[c%10]==1) return 0;
            else flag[c%10]=1  ;

            a=a/10;
            b=b/10;
            c=c/10;

        }
        return 1;
    }

    public static void main(String[] args) {

        int ans=0;

        for(int a=123;a<=987;a++)
            for(int b=123;b<=987-a;b++)
            {
                int c=a+b;
                if(check(a,b,c)==1)
                {
                    ans++;
                    System.out.println(a+"+"+b+"="+c);
                }

            }
        System.out.println(ans);
    }
}

🌊 4.2求值

学习了约数后，小明对于约数很好奇，他发现，给定一个正整数 tt，总是可以找到含有 tt 个约数的整数。小明对于含有 tt 个约数的最小数非常感兴趣，并把它定义为 S_tSt​ 。

例如 S1 = 1, S2 = 2, S3 = 4, S4 = 6，· · ·S1​=1,S2​=2,S3​=4,S4​=6，⋅⋅⋅ 。

现在小明想知道，当 t=100 时，St​100是多少？即 S1​00 是多少？

题目链接：求值

      题目的要求就是找一个最小的有100个因数的数，我们写一个计算因数个数的方法，然后从1开始往后遍历即可。**这里推荐大家计算因数个数的方法不要去优化，防止一些细节出问题，数据量不大，从1遍历到n就好。我们的目的是为了得到正确答案，在可以的情况下，尽量不优化代码防止出错。****        **

public class 求值 {
    public static void main(String[] args) {
        int count=1;
        //在到达1000000前肯定能得到答案的
        for(;count<=1000000;count++) {
            if(check(count)==100) break;
        }
        System.out.println(count);//45360
    }
    static int check(int n) {
        int ans=0;
        //朴素遍历无需优化
        for(int i=1;i<=n;i++) {
            if(n%i==0) ans++;
        }
        return ans;
    }
}

🍒5.经典必做大题系列

🚀5.1k倍区间

题目链接：k倍区间

   之所以会说这道题，是因为这道题在蓝桥杯中的大题中算简单的。力扣甚至有和它一样的原题（而且只是mid的难度）。只不过有一点区别，但是做法几乎是完全一样的。首先和大家讲明一个定理——**同余定理**

同予定理——想要 b - a为 k 的倍数，只需要确保 b 和 a 模 k 相同即可

     掌握了这个定理，我们就能去分析题目了。首先**要找子数组，肯定要想到利用前缀和数组去查找（没想到的要反省了）。**当在前缀和数组中遍历到第i个时，此时获得arr[i]%k的值，此时i的左边（也就是[0,i-1]区间）我们取为j，如果arr[j]%k==arr[i]%k，说明[j,i]这个区间和是k的倍数。根据以上写出代码

import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;

public class k倍区间 {
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        int N=sc.nextInt();
        int k=sc.nextInt();
        //注意要用long数组,数据量较大
        long[] arr=new long[N+1];
        //Map前面也得用Long,因为有long参与的运算返回值也是long
        Map<Long,Integer> map=new HashMap<Long,Integer>();
        //获得前缀和数组
        for(int i=0;i<N;++i) {
            arr[i+1]=arr[i]+sc.nextLong();
        }
        long ans=0;
        //千万不能忘记把这个忘记放入
        map.put(0L,1);
        for(int i=1;i<=N;++i) {
            ans+=map.getOrDefault(arr[i]%k, 0);
            map.put(arr[i]%k, map.getOrDefault(arr[i]%k, 0)+1);
        }
        System.out.println(ans);
    }
}

    放到蓝桥OJ上取跑一跑满分没问题。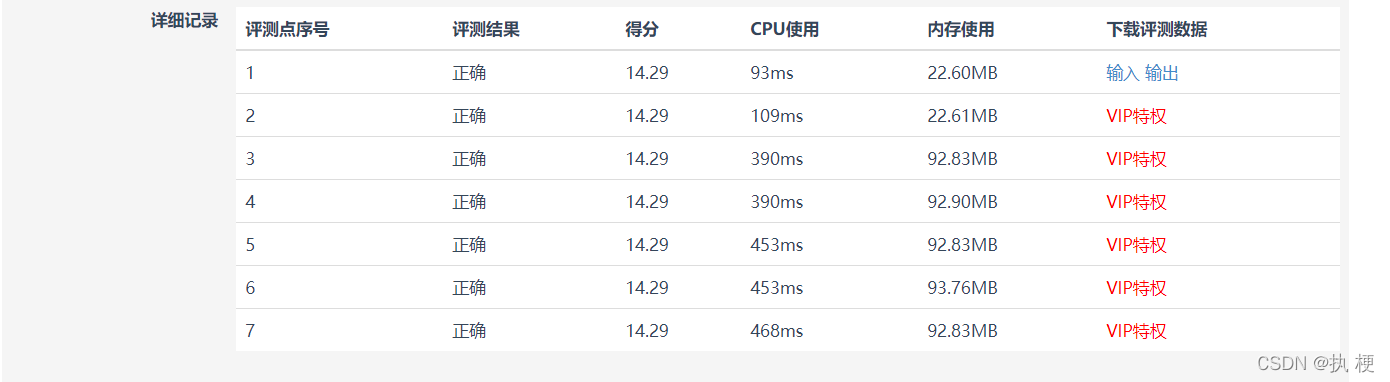![](https://img-blog.csdnimg.cn/3e0c3eea5a5343799637d47e95899774.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5omnIOailw==,size_20,color_FFFFFF,t_70,g_se,x_16)

✈️5.2子串分值

 题目链接：子串分值 

 题目分析：这道题是可以暴力做的，可以拿到60分。每次计算以S[i]为字符串的头往后遍历计算可以获得的分数。对于S[i,j]的子数组中只出现一次的元素我们可以通过S[i,j-1]去获得，用不着每次都遍历。这里我用一个Set去记录只出现一次的元素，再用一个Set记录重复出现过的元素（感觉可以优化但是没有去优化）

public class 子串分值 {
    //过了6个得了六十分
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String s=sc.next();
        int count=0;
        int n=s.length();  
        for(int i=0;i<n;++i){
            int ans=1;
            //放只出现一次的字符
            Set<Character> set1=new HashSet<>();
            //放多次出现的字符
            Set<Character> set2=new HashSet<>();
            set1.add(s.charAt(i));
            for(int j=i+1;j<n;++j) {
                char c=s.charAt(j);
                if(set1.contains(c)) {
                    set1.remove(c);
                    set2.add(c);
                }else if(!set1.contains(c)&&!set2.contains(c)) {
                    set1.add(c);
                }
                //set1的长度即是只出现了一次的元素
                ans+=set1.size();
            }
            count+=ans;
        }
        System.out.println(count);
    }
}

    **满分做法：**

** 做到这里，我们可以去分析一下。一个字符什么时候可以贡献分数？**

    **题目要求******在**一个字符串中，只有只出现一次的元素可以得分。所以说明什么适合它不能得分呢？**是不是就是当它和前一个和它相同的字符或者后一个和它相同的字符在一个区间时，它就无法得分。我以**a**bcd**a**ef**a**为例：中间这个a在不和它前一个a和后一个a在同一个子串中时，它都可以得分。换个说法：这个a只有在bcd**a**ef这个区间内的它才可以得分。**画个草图给大家理解下**![](https://img-blog.csdnimg.cn/93154d2651b24d3eb2cd0fd8fa84bc3b.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5omnIOailw==,size_20,color_FFFFFF,t_70,g_se,x_16)

     **通过上面的思路我们去算出所有的字符的得分就是我们的答案。以图中j位置的a为例，前一个a的元素为i（没有则记为-1），后一个a的位置为k（没有则记为n）。则j位置的a的得分就是（j-i）(k-j)。所以基于此思路我们需要用一个数组pre记录每个字符前一次出现的位置，next为后一次出现的位置。一个数组where记录每个字符最后一次出现的下标。难点在于三个数组的更新，得到三个数组后答案就很好得到了。**

import java.util.Arrays;
import java.util.Scanner;

public class 子串分值2 {
    //满分答案
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        String s=sc.next();
        int n=s.length();
        //记录每个字符a在前一次出现的位置，如果没有则为-1
        int[] pre=new int[n];
        //记录每个字符a在后一次出现的位置，如果没有则为n
        int[] next=new int[n];
        int[] where=new int[26];//统计每个字符最后一次出现的下标
        Arrays.fill(where, -1);
        //这样能得到i处字符前一次出现的位置
        for(int i=0;i<n;++i) {
            pre[i]=where[s.charAt(i)-'a'];
            where[s.charAt(i)-'a']=i;
        }
        Arrays.fill(where, n);
        for(int i=n-1;i>=0;i--) {
            next[i]=where[s.charAt(i)-'a'];
            where[s.charAt(i)-'a']=i;
        }
        //统计答案 
        int ans=0;
        for(int j=0;j<n;++j) {
            ans+=(j-pre[j])*(next[j]-j);
        }
        System.out.println(ans);
    }
}

    拿去跑跑果不其然拿了满分😆

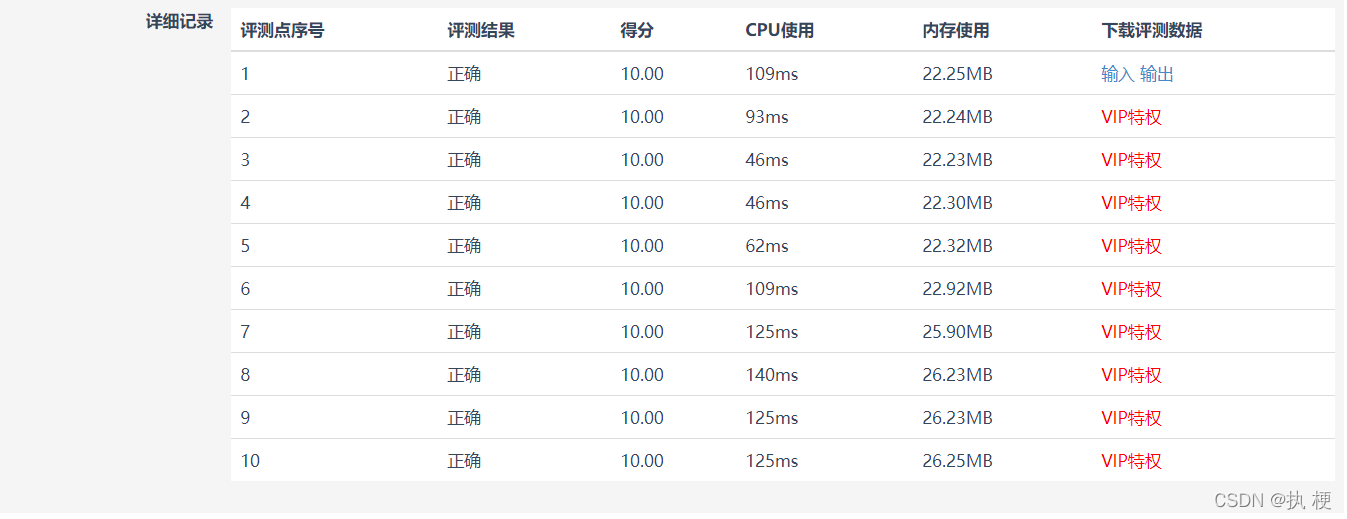
    最后一个月也希望大家好好努力，一起打进国赛（**先把门票费挣回来再说哈哈哈**）！

** 有用的兄弟当然也求给个三连，非常感谢！！！**

** **