目录
一、求最大公约数的三种方法
二、主函数及运行结果
三、小结
一、求最大公约数的三种方法
1、暴力穷举法
将m,n中较小数赋值给cd,将cd作为除数,cd通过自减在循环寻找满足(m%cd==0&&n%cd==0)的数作为最大公约数
2、辗转相减法
T为最大公约数,a=mT,b=nT,a-b=(m-n)T,两个数据的差值具有和原始数据相同的最大公约数,通过循环使大的数减小的数直到m-n的最小值为0,此时a=b,a与b为最大公约数
3、辗转相除法
T是m,n的最大公约数,T能整除m,也能整除n,那么就必定能整除(m-n),所以T也是(m-n)的公约数,若m>n,则(m/n)的余数依旧有最大公约数
通过较大数与较小数之间的不断取余得到最大公约数
1、暴力穷举法
int CommonDivisor(int m, int n){
if (m<n){
int temp = m;
int m = n;
int n = temp;
}
int cd = n;
while (cd>0){
if (m%cd==0&&n%cd==0){
break;
}
cd--;
}
return cd;
}
2、辗转相减法
int CommonDivisor(int m, int n){
while (m!=n){
if (m>n){
m -= n;
}
else{
n -= m;
}
}
return n;
}
3、辗转相除法
int CommonDivisor(int m, int n){
while (m*n!=0){
if (m>n){
m %= n;
}
else{
n %= m;
}
}
return m+n;
}
二、主函数及运行结果
主函数
#include<stdio.h>
#include<windows.h>
int main(){
int a = 0;
int b = 0;
printf("请输入两个数:");
scanf("%d %d",&a,&b);
int z = CommonDivisor(a,b);
printf("最大公约数为:%d\n",z);
system("pause");
return 0;
}
运行结果
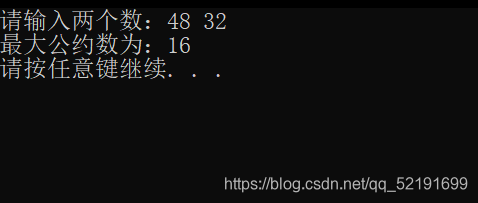
三、小结
求最大公约数的三种方法第一种为穷举,虽然简单但循环次数太多,浪费资源和内存。辗转相减、相除法为更好的方法,需要我们正确理解求差和求余的值也有同样的公约数。多了解,多分析,代码的知识面就拓展开了,从大家那里学到了很多。
版权归原作者 语风之 所有, 如有侵权,请联系我们删除。