点击上方“Deephub Imba”,关注公众号,好文章不错过 !
我们的项目并不总是有充足的数据。通常,我们只有一个样本数据集可供使用,由于缺乏资源我们无法执行重复实验(例如A/B测试)。
幸运的是,我们有重采样的方法来充分利用我们所拥有的数据。自举法(Bootstrapping)是一种重采样技术,可以为我们解决这个问题。虽然我们可能对自举法背后的“为什么”和“如何”很熟悉,但这篇文章旨在以一种为外行介绍的方式展示自举法的“为什么”。
自举法的快速回顾
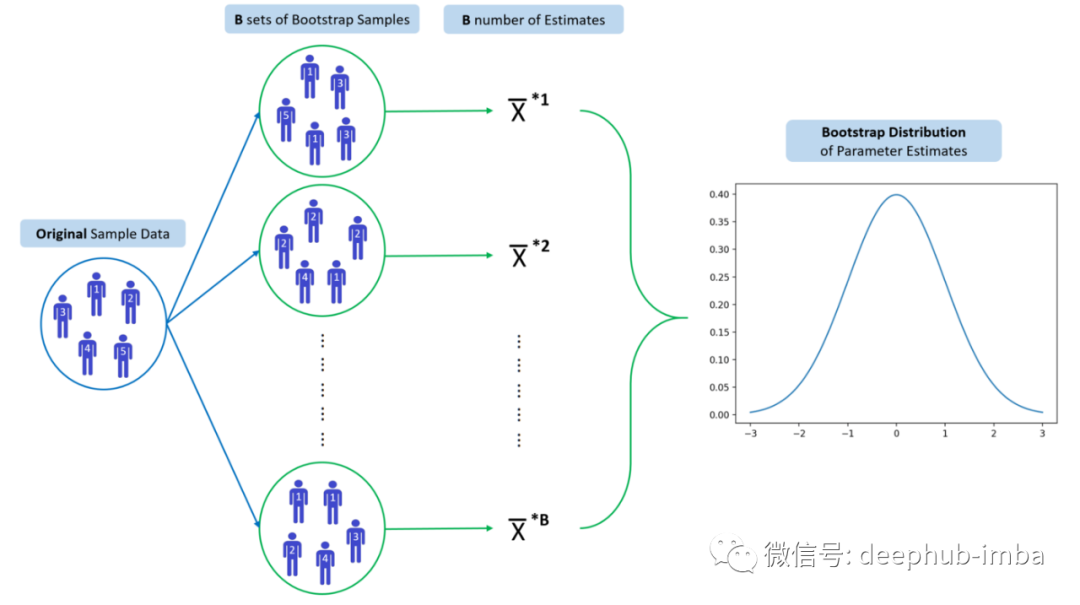
自举法的目标是基于从原始样本中获得的多个数据样本,为总体参数(例如总体均值 θ)创建一个估计值(例如样本均值 x̄)。
自举法 是通过重复采样(替换)样本数据集来创建许多模拟样本来完成的。每个模拟的样本被用来计算参数的估计,然后这些估计被组合起来形成一个抽样分布。
然后,自举抽样分布允许我们得出统计推论,如估计参数的标准误差。
为什么自举法是有效的?
你一定想知道,重复采样同一个样本数据集的行为怎么能让我们对总体统计数据做出推论呢?
理想情况下,我们希望从真实的总体中提取多个独立的真实样本以理解总体统计数据。然而我们已经确定,这可能并不总是可行的。因此我们必须使用样本数据集,这是我们拥有的关于总体的最好(也是唯一)信息。
自举法合理的假设是,大多数样本(如果是随机抽取的)将看起来与它们的总体非常相似。这意味着我们的样本数据可以被视为一个总体,我们现在假装它代表真实的总体(一定要记住这一点)。
有了这个假设群体,我们可以从中抽取多个(自举)随机样本。这就好像我们从真实总体中获得了多个样本。
注:实际上,原始样本只是真实总体中的一个样本。
由于允许进行置换抽样,所以自举的样本也可以看作是在不同方法和假设下产生的随机样本。
从这些自举样本中汇总的抽样信息最终将帮助我们获得(相对)准确的总体参数估计值,例如总体均值。
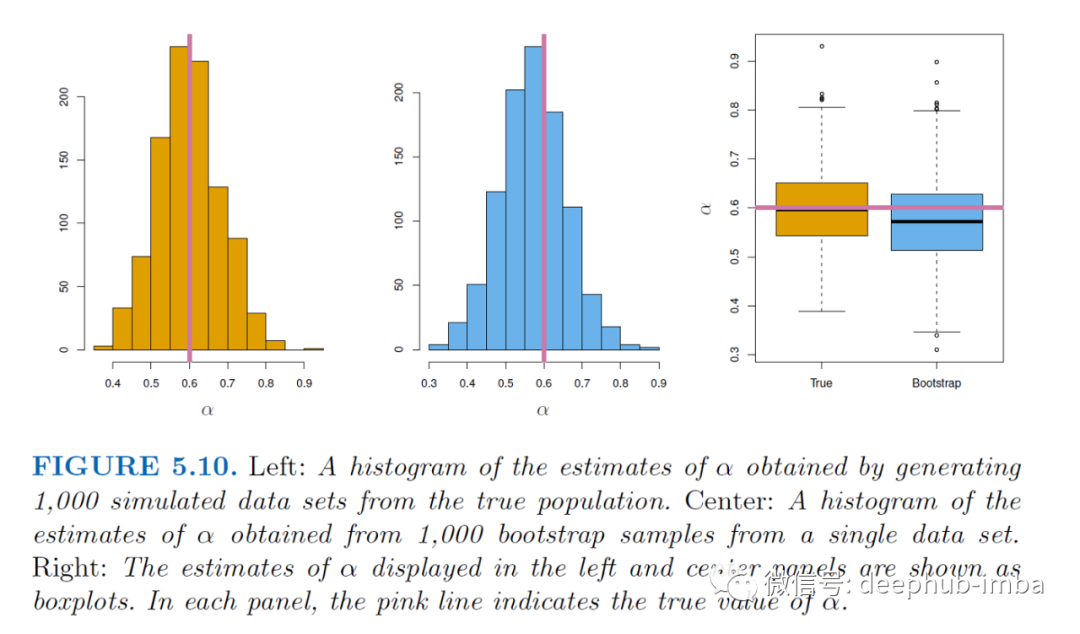
那么自举抽样的效果如何呢?上图比较了来自真实总体的 1,000 个模拟样本与 1,000 个引导样本的参数 (α) 估计值。
我们可以看到箱线图具有相似的散布,表明自举法可以有效地估计与参数估计相关的可变性。
总结
在本文中,我们探索了自举发理论的简单解释。希望这篇文章能让您更好地了解自举,以及为什么它在理论上和实践中都有效。
关键概念是假设原始样本代表总体。通过多次重采样这个样本,我们得到了总体参数的样本估计的一个相对准确的抽样分布。
当然,这有几个注意事项。例如,在从真实总体中抽样的正常情况下,我们永远不会抽取与整个总体相同大小的样本。但是,在自举中使用与原始数据集相同的样本大小是很常见的。
作者:Kenneth Leung
喜欢就关注一下吧:
点个 在看 你最好看!********** **********