LSTM和双向LSTM讲解及实践

目录：

• RNN的长期依赖问题
• LSTM原理讲解
• 双向LSTM原理讲解
• keras实现LSTM和双向LSTM

RNN 的长期依赖问题

在上篇文章中介绍的循环神经网络RNN在训练的过程中会有长期依赖的问题，这是由于RNN模型在训练时会遇到梯度消失(大部分情况)或者梯度爆炸(很少，但对优化过程影响很大)的问题。对于梯度爆炸是很好解决的，可以使用梯度修剪(Gradient Clipping)，即当梯度向量大于某个阈值，缩放梯度向量。但对于梯度消失是很难解决的。所谓的梯度消失或梯度爆炸是指训练时计算和反向传播，梯度倾向于在每一时刻递减或递增，经过一段时间后，梯度就会收敛到零(消失)或发散到无穷大(爆炸)。简单来说，长期依赖的问题就是在每一个时间的间隔不断增大时，RNN会丧失到连接到远处信息的能力。

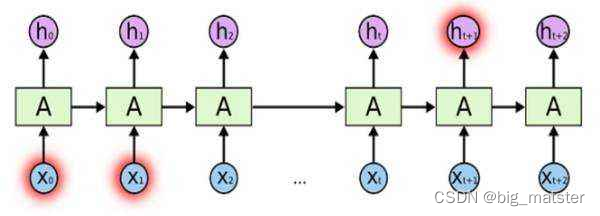
如下图，随着时间点t的不断递增，当t时刻和0时刻的时间间隔较大的时候，

     t 
    
   
  
    t 
   
  
t时刻的记忆 
 
  
   
   
     h 
    
   
     t 
    
   
  
    ht 
   
  
ht可能已经**丧失了学习连接到远处0时刻的信息的能力了**。

假定

      x 
     
    
      0 
     
    
   
  
    x_0 
   
  
x0​,的输入为“**我住在深圳**”。后面插入了很多其他的句子，然后在 
 
  
   
    
    
      x 
     
    
      t 
     
    
   
  
    x_t 
   
  
xt​输入了：我**在市政府上班**，由于 
 
  
   
    
    
      x 
     
    
      0 
     
    
   
     和 
    
    
    
      x 
     
    
      t 
     
    
   
  
    x_0和x_t 
   
  
x0​和xt​相差很远，当RNN输入到 
 
  
   
    
    
      x 
     
    
      t 
     
    
   
  
    x_t 
   
  
xt​时， 
 
  
   
   
     t 
    
   
  
    t 
   
  
t时刻的记忆已经丧失了 
 
  
   
    
    
      x 
     
    
      0 
     
    
   
  
    x_0 
   
  
x0​时保存的信息啦。因此 
 
  
   
    
    
      x 
     
    
      t 
     
    
   
  
    x_t 
   
  
xt​时刻的神经网络已经无法理解到我是在那**个城市的市政府上班啦**。

LSTM原理讲解

在理论上， RNN绝对可以处理这样长度依赖问题，人们可以仔细的挑选参数来解决这类问题中的最初级形式。但在实践中，RNN却不能够成功的学习到这些知识，因此，LSTM就是为了解决长期依赖问题而生的，LSTM通过刻意的设计来避免长期依赖问题。记住长期的信息在实践中，是LSTM默认行为。而非需要付出很大的代价才能才能获得的能力。
所有的RNN都具有一种重复神经网络模块的链式的形式。在标准的RNN中，这个重复的模块只有一个非常简单的结构。例如一个

     t 
    
   
     a 
    
   
     n 
    
   
     h 
    
   
     层 
    
   
  
    tanh层 
   
  
tanh层

LSTM同样是这样结构，但是重复的模块拥有一个不同的结构，不同于，单一神经网络层， 这里有四个，以一种非常特殊的方式进行交互。

先介绍上图中符号的含义: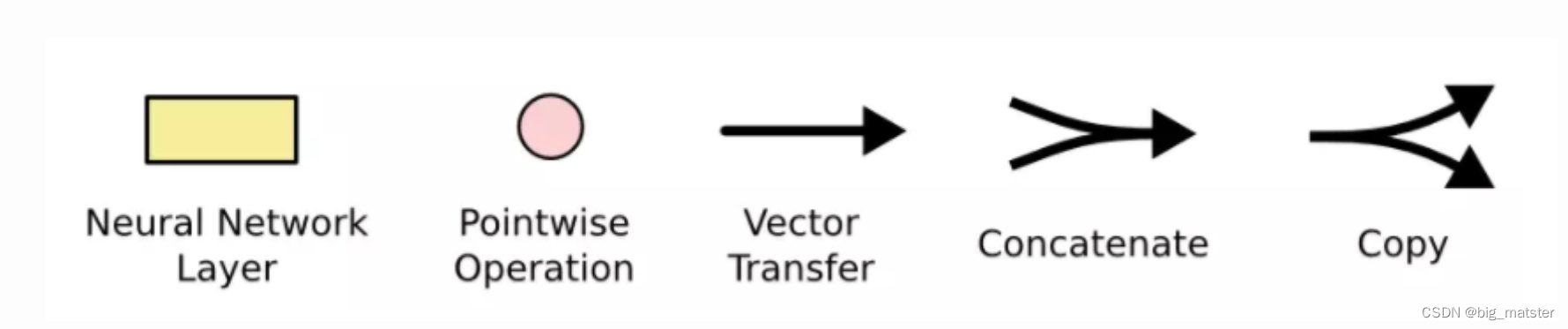

在上面的图例中，每一条黑线都传输着一整个向量。从一个节点的输出到其他节点的输入。粉色的圈代表

     p 
    
   
     o 
    
   
     i 
    
   
     n 
    
   
     t 
    
   
     w 
    
   
     i 
    
   
     s 
    
   
     e 
    
   
  
    pointwise 
   
  
pointwise操作。

诸如向量的和，而黄色的矩阵都是学习到的神经网络层。
合在一起的线表示向量的连接。分开的线表示内容被复制。
然后分发到不同位置。

接下来将对LSTM进行逐步理解，在每个记忆单元（图中A）中包括细胞状态

      c 
     
    
      t 
     
    
   
  
    c_t 
   
  
ct​,**遗忘门、输入门和输出门**。这些**门结构能够让信息选择性的通过**。用**来去除和增加信息到细胞状态**。

细胞状态（

      c 
     
    
      t 
     
    
   
  
    c_t 
   
  
ct​)


 
  
   
   
     t 
    
   
  
    t 
   
  
t时刻记忆信息，**用来保存重要信息**。就好像我们的笔记本一样，保存了我们以前学过的知识点，如**下图的水平线从图上方贯穿运行**。**直接在整个链上运行**，使得**信息在上面流传保持不变会很容易**。

遗忘门

控制遗忘上一层细胞状态的内容，根据上一序列

      h 
     
     
     
       t 
      
     
       − 
      
     
       1 
      
     
    
   
  
    h_{t-1} 
   
  
ht−1​,

和本序列

      x 
     
    
      t 
     
    
   
  
    x_t 
   
  
xt​为输入。通过 
 
  
   
   
     S 
    
   
     i 
    
   
     g 
    
   
     m 
    
   
     o 
    
   
     i 
    
   
     d 
    
   
  
    Sigmoid 
   
  
Sigmoid激活函数，得到**上一层细胞状态内容那些需要去除**。那些需要保留。值得注意的是：

该输入是以向量的形式，我们希望遗忘门输出的值大多为0或1. j即对向量中的每个值是完全忘记或完全记住。
因此，我们使用的是

     S 
    
   
     i 
    
   
     g 
    
   
     m 
    
   
     o 
    
   
     i 
    
   
     d 
    
   
  
    Sigmoid 
   
  
Sigmoid作为激活函数，因为该函数在许多取值范围内的值都接近于0和1.（**这里不能用阶跃函数作为激活函数**）因此其在所有位置的梯度都为0，无法作为激活函数，其他们使用 
 
  
   
   
     S 
    
   
     i 
    
   
     g 
    
   
     m 
    
   
     o 
    
   
     i 
    
   
     d 
    
   
  
    Sigmoid 
   
  
Sigmoid函数同理。因此，虽然在**其他神经网咯可以变换激活函数**。但并**不建议变换LSTM的激活函数**。

以上一个例子来说明遗忘门的作用。在语言模型中，细胞状态可以保存着这样重要的信息。当前主语为单数或复数等，如当前的主语为"小明“如当前的主语为“小明”，当输入为“同学们”，此时遗传门就要开始“干活”了，将“小明”遗忘，主语为单数形式遗忘。

输入门

处理当前序列位置的输入，确定需要更新的信息。去更新细胞状态。此过程分为两部分：

• 一部分使用包含 s i g m o i d sigmoid sigmoid层的输入们决定那些信息该被加入到细胞状态。
• 确定了那些信息要加入后，需要将新信息转换成能够加入到细胞状态的形式。所以，另一部分是使用 t a n h tanh tanh函数，产生一个新的候选向量。（可以这么理解，LSTM的做法是对信息都转为能加入细胞状态的形式，然后再通过第一部分得到的结果，确定其中那些信息加入到细胞状态。） 有了遗忘门和输入门，现在我们就能把细胞状态 C t − 1 C_{t-1} Ct−1​更新为 C t C_t Ct​,如下图所示：其中 f t × C t − 1 f_t \times C_{t-1} ft​×Ct−1​表示希望删除的信息， i t × C t it \times C_t it×Ct​表示新增的信息。

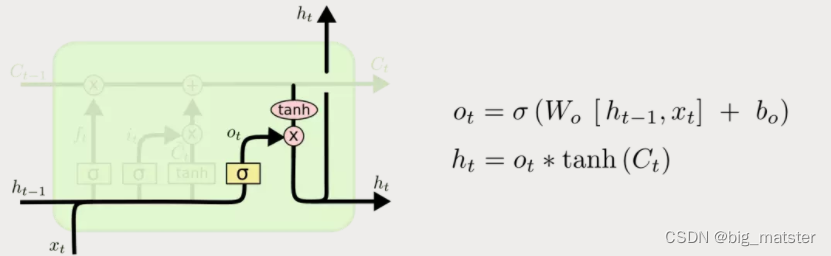
输出门

最后要基于细胞状态保存的内容来确定输出什么内容。即选择性的输出细胞状态保存的内容。类似于输入门两部分实现更新一样，输出门也是需要使用sigmoid激活函数确定哪个部分的内容需要输出，然后再使用tanh激活函数对细胞状态的内容进行处理(因为通过上面计算得到的Ct每个值不是在tanh的取值范围-1~1中，需要调整)，将这两部分相乘就得到了我们希望输出的那部分。

举个例子，同样在语言模型中，细胞状态中此时包含很多重要的信息，比如：主语为单数形式、时态为过去时态、主语的性别为男性等。此时输入为一个主语，可能需要输出与动词相关的信息。这时候只需要输出的是单数的形式和时态为过程。而不需要输出主语性别就可以确定动词词性的变化。

双向LSTM

如上篇文章BRNN所述同理，有时候预测可能需要由前面若干输入后面若干输入共同决定。这样会更加准确，因此，提出了双向循环神经网络。网络结构如下图：可以看到

     f 
    
   
     o 
    
   
     r 
    
   
     w 
    
   
     a 
    
   
     r 
    
   
     层 
    
   
  
    forwar层 
   
  
forwar层和 
 
  
   
   
     B 
    
   
     a 
    
   
     c 
    
   
     k 
    
   
     w 
    
   
     a 
    
   
     r 
    
   
     d 
    
   
     层 
    
   
  
    Backward层 
   
  
Backward层，共同连接着输出层，其中包含着六个共享权值 
 
  
   
   
     w 
    
   
     1 
    
   
     − 
    
   
     w 
    
   
     6 
    
   
  
    w1-w6 
   
  
w1−w6.

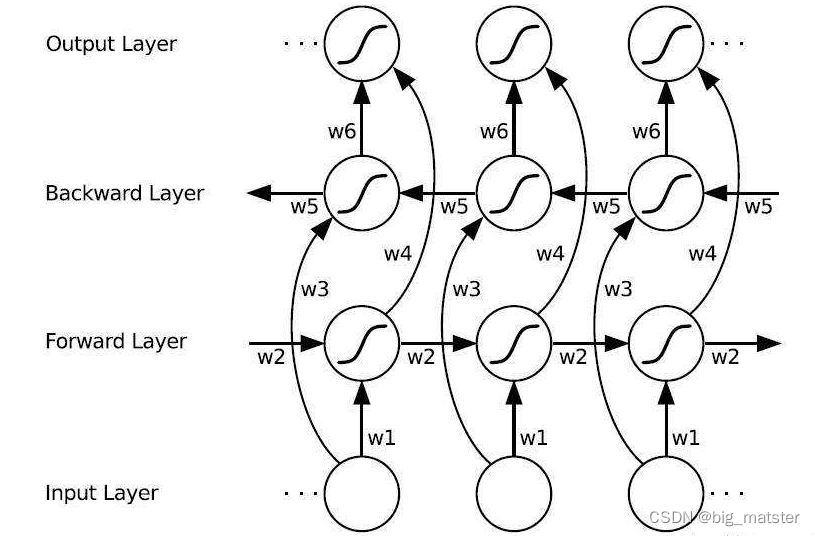
在Forward层从

     1 
    
   
  
    1 
   
  
1时刻到 
 
  
   
   
     t 
    
   
  
    t 
   
  
t时刻，正向计算一遍。得到**并保存每个时刻向前隐含层的输出**。在 
 
  
   
   
     B 
    
   
     a 
    
   
     c 
    
   
     k 
    
   
     w 
    
   
     a 
    
   
     r 
    
   
     d 
    
   
  
    Backward 
   
  
Backward层中，沿着时刻 
 
  
   
   
     t 
    
   
  
    t 
   
  
t和时刻 
 
  
   
   
     1 
    
   
  
    1 
   
  
1反向计算一遍，得到并**保存每个时刻向后隐含层的输出**。

最后在每个时刻，结合

     F 
    
   
     o 
    
   
     r 
    
   
     w 
    
   
     a 
    
   
     r 
    
   
     d 
    
   
     层 
    
   
     和 
    
   
     B 
    
   
     a 
    
   
     c 
    
   
     k 
    
   
     w 
    
   
     a 
    
   
     r 
    
   
     d 
    
   
     层 
    
   
  
    Forward层和Backward层 
   
  
Forward层和Backward层的相应时刻输出的结果得到最终的输出，用数学表达式计算如下：

有的问题，其实稍微看一遍都可以明白了。

keras实现LSTM和双向LSTM

keras对神经网络的支持和封装，在上一篇文章中已经讲解了，在这里仅介绍两个模型的搭建，如雨疑问，请阅读keras系列的上一篇文章。

LSTM模型

Bi-LSTM模型

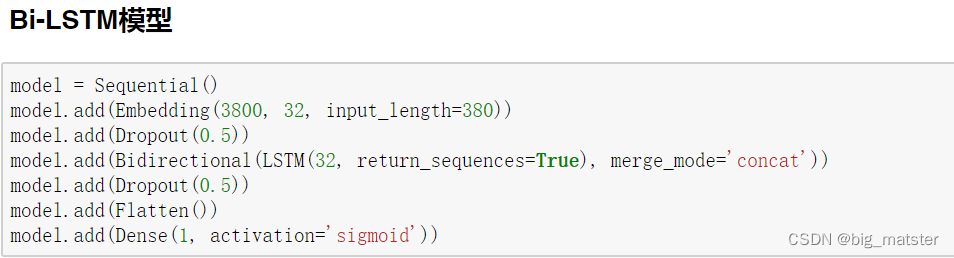
训练模型

预测

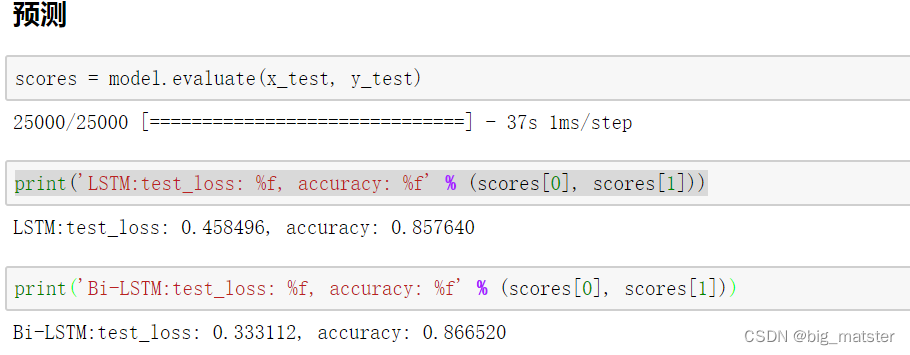
总结

慢慢的将各种模型都罗列出来，全部都将其搞定都行啦的样子打算。