PyMC3(现在简称为PyMC)是一个贝叶斯建模包,它使数据科学家能够轻松地进行贝叶斯推断。

PyMC3采用马尔可夫链蒙特卡罗(MCMC)方法计算后验分布。这个方法相当复杂,原理方面我们这里不做详细描述,这里只说明一些简单的概念,为什么使用MCMC呢?
这是为了避开贝叶斯定理中计算归一化常数的棘手问题:
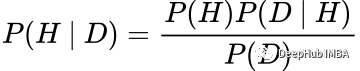
其中P(H | D)为后验,P(H)为先验,P(D | H)为似然,P(D)为归一化常数,定义为:
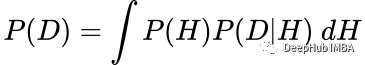
对于许多问题,这个积分要么没有封闭形式的解,要么无法计算。所以才有MCMC等方法被开发出来解决这个问题,并允许我们使用贝叶斯方法。
此外还有一种叫做共轭先验(Conjugate Priors)的方法也能解决这个问题,但它的可延展性不如MCMC。如果你想了解更多关于共轭先验的知识,我们在后面其他文章进行讲解。
在这篇文章中,我们将介绍如何使用PyMC3包实现贝叶斯线性回归,并快速介绍它与普通线性回归的区别。
贝叶斯vs频率回归
频率主义和贝叶斯回归方法之间的关键区别在于他们如何处理参数。在频率统计中,线性回归模型的参数是固定的,而在贝叶斯统计中,它们是随机变量。
频率主义者使用极大似然估计(MLE)的方法来推导线性回归模型的值。MLE的结果是每个参数的一个固定值。
在贝叶斯世界中,参数是具有一定概率的值分布,使用更多的数据更新这个分布,这样我们就可以更加确定参数可以取的值。这个过程被称为贝叶斯更新
有了上面的简单介绍,我们已经知道了贝叶斯和频率回归之间的主要区别。下面开始正题
使用PyMC3
首先导入包:
import pymc3 as pm
import arviz as az
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from scipy.stats import norm
import statsmodels.formula.api as smf
如果想安装PyMC3和ArviZ,请查看他们网站上的安装说明。现在我们使用sklearn中的make_regression函数生成一些数据:
x, y = datasets.make_regression(n_samples=10_000,
n_features=1,
noise=10,
bias=5)
data = pd.DataFrame(list(zip(x.flatten(), y)),columns =['x', 'y'])
fig, ax = plt.subplots(figsize=(9,5))
ax.scatter(data['x'], data['y'])
ax.ticklabel_format(style='plain')
plt.xlabel('x',fontsize=18)
plt.ylabel('y',fontsize=18)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.show()
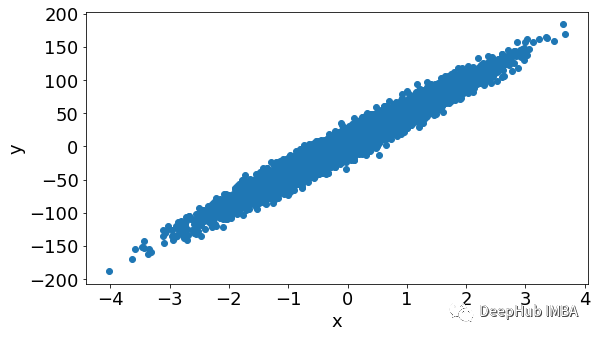
我们先使用频率论的常见回归,使用普通最小二乘(OLS)方法绘制频率线性回归线:
formula = 'y ~ x'
results = smf.ols(formula, data=data).fit()
results.params
inter = results.params['Intercept']
slope = results.params['x']
x_vals = np.arange(min(x), max(x), 0.1)
ols_line = inter + slope * x_vals
fig, ax = plt.subplots(figsize=(9,5))
ax.scatter(data['x'], data['y'])
ax.plot(x_vals, ols_line,label='OLS Fit', color='red')
ax.ticklabel_format(style='plain')
plt.xlabel('x',fontsize=18)
plt.ylabel('y',fontsize=18)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.legend(fontsize=16)
plt.show()
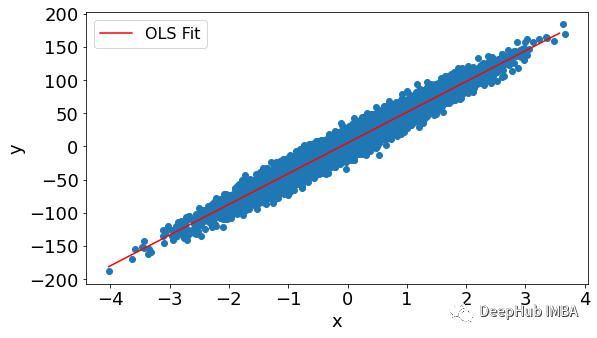
上面的结果我们作为基线模型与我们后面的贝叶斯回归进行对比
要使用PyMC3,我们必须初始化一个模型,选择先验并告诉模型后验分布应该是什么,我们使用100个样本来进行建模,:
# Start our model
with pm.Model() as model_100:
grad = pm.Uniform("grad",
lower=results.params['x']*0.5,
upper=results.params['x']*1.5)
inter = pm.Uniform("inter",
lower=results.params['Intercept']*0.5,
upper=results.params['Intercept']*1.5)
sigma = pm.Uniform("sigma",
lower=results.resid.std()*0.5,\
upper=results.resid.std()*1.5)
# Linear regression line
mean = inter + grad*data['x']
# Describe the distribution of our conditional output
y = pm.Normal('y', mu = mean, sd = sigma, observed = data['y'])
# Run the sampling using pymc3 for 100 samples
trace_100 = pm.sample(100,return_inferencedata=True)
该代码将运行MCMC采样器来计算每个参数的后验值,绘制每个参数的后验分布:
with model_100:
az.plot_posterior(trace_100,
var_names=['grad', 'inter', 'sigma'],
textsize=18,
point_estimate='mean',
rope_color='black')
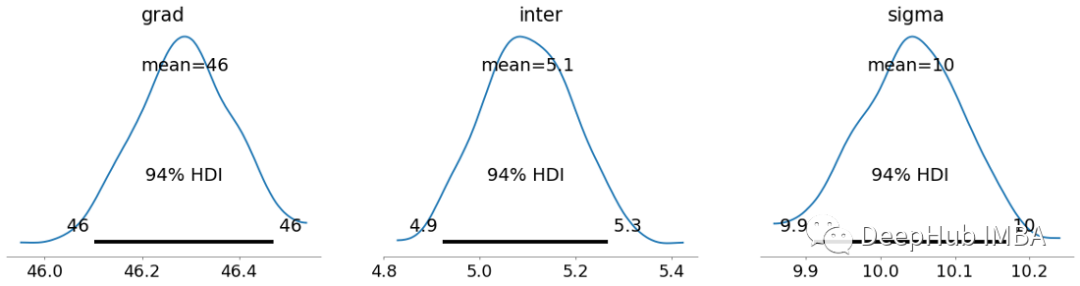
可以看到这些后验分布的平均值与OLS估计相同,但对于贝叶斯回归来说并不是参数可以采用的唯一值。这里有很多值,这是贝叶斯线性回归的主要核心之一。HDI代表高密度区间(High Density Interval),它描述了我们在参数估计中的确定性。
这个模拟只使用了数据中的100个样本。和其他方法一样,数据越多,贝叶斯方法就越确定。现在我们使用10000个样本,再次运行这个过程:
with pm.Model() as model_10_100:
grad = pm.Uniform("grad",
lower=results.params['x']*0.5,
upper=results.params['x']*1.5)
inter = pm.Uniform("inter",
lower=results.params['Intercept']*0.5,
upper=results.params['Intercept']*1.5)
sigma = pm.Uniform("sigma",
lower=results.resid.std()*0.5,
upper=results.resid.std()*1.5)
# Linear regression line
mean = inter + grad*data['x']
# Describe the distribution of our conditional output
y = pm.Normal('y', mu = mean, sd = sigma, observed = data['y'])
# Run the sampling using pymc3 for 10,000 samples
trace_10_000 = pm.sample(10_000,return_inferencedata=True)
看看参数的后验分布:
with model_10_100:
az.plot_posterior(trace_10_000,
var_names=['grad', 'inter', 'sigma'],
textsize=18,
point_estimate='mean',
rope_color='black')
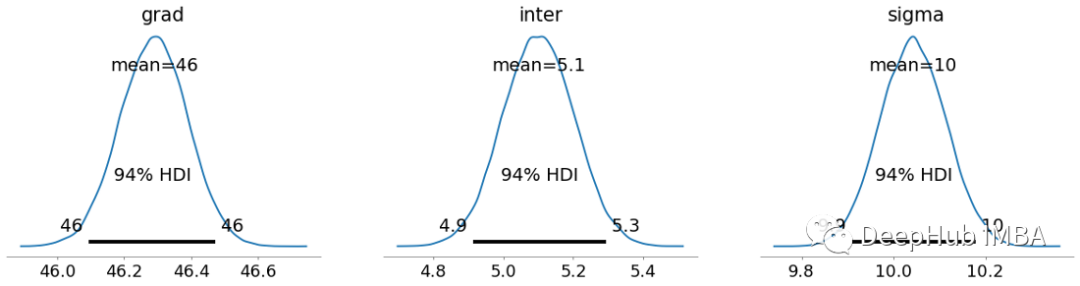
可以看到平均值的预测并没有改变,但是随着对参数的分布更加确定,总体上的分布变得更加平滑和紧凑。
总结
在本文中,我们介绍贝叶斯统计的主要原理,并解释了它与频率统计相比如何采用不同的方法进行线性回归。然后,我们学习了如何使用PyMC3包执行贝叶斯回归的基本示例。
本文的代码:
https://github.com/egorhowell/Medium-Articles/blob/main/Statistics/pymc3_tutorial.ipynb
作者:Egor Howell