使用 Numpy 创建自己的深度学习框架

本文并不是为了造轮子，只是通过手动实现来介绍建基本深度学习框架所需组件和步骤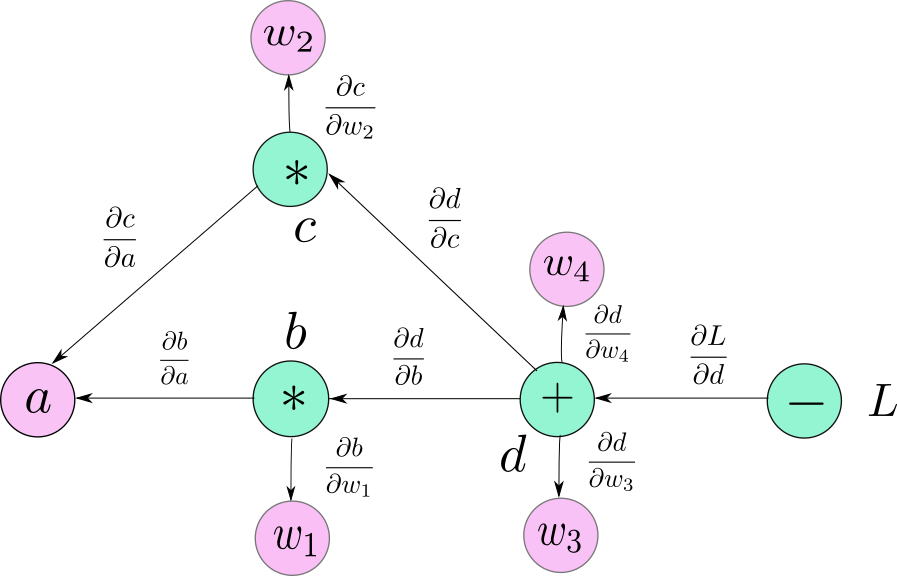

Numpy 已经提供了基本上所有需要的计算操作，我们需要的是一个支持自动微分（autograd）的框架来计算多个操作的梯度，这是模块化方法构建神经网络层的标准化方法，通过自动微分的框架，我们可以将优化器、激活函数等组合在一起用于训练神经网络。

所以一个基本的深度学习框架的组件总结如下：

• 一个autograd系统
• 神经网络层
• 神经网络模型
• 优化器
• 激活函数
• 数据集

接下来，我们将逐一介绍这些组件，看看它们的作用以及如何使用他们，这里将使用 gradflow（这是一个个人开源教育 autograd 系统）因为它支持深度神经网络，并且和 PyTorch API基本一致。

Autograd系统

这是最重要的组成部分，它是每个深度学习框架的基础，因为系统将跟踪应用于输入张量的操作，并使用损失函数针对于每个参数的梯度来更新模型的权重。这里的一个必要条件是这些操作必须是可微的。

我们的 autograd 系统的基础是变量，通过为我们需要的操作实现 dunder 方法（dunder 方法 ：Python中以双下划线开头的特殊方法），我们将能够跟踪每个实例的父实例是什么以及如何为它们计算梯度。为了帮助进行一些操作，我们将使用一个 numpy 数组来保存实际数据。

变量的另一个重要部分是反向传播方法，这将计算当前实例相对于计算图中每个父类祖先的梯度。在具体步骤中，我们将使用父级的引用和原始操作中嵌入的梯度函数来更新 grad 成员字段。

以下代码片段包含主变量类初始化函数、添加操作的 dunder 方法和反向传播方法：

class Variable:
    def __init__(
        self, 
        data: np.ndarray, 
        parents: Tuple[Variable] = None, 
        requires_grad: bool = False
    ) -> None:
        self.data = data
        self.grad: Union[int, None] = .0 if requires_grad else None
        self.parents = parents or ()
        self._requires_grad = requires_grad
        self._back_grad_fn = lambda: None

    def __add__(self, other: Variable) -> Variable:
        if not isinstance(other, Variable):
            raise TypeError("The second operator must be a Variable type")

        result = self.data + other.data
        variable = Variable(result, parents=(self, other))

        if any((parent.requires_grad for parent in variable.parents)):
            variable.requires_grad = True

            def _back_grad_fn():
                self.grad += variable.grad
                other.grad += variable.grad

            variable._back_grad_fn = _back_grad_fn
        return variable

      
    def backward(self, grad: Variable | np.ndarray = None) -> None:
        if grad is None:
            grad = np.array([1])
          
        self.grad = grad
        variable_queue = [self]

        while len(variable_queue):
            variable = variable_queue.pop(0)
            variable._back_grad_fn()
            variable_queue.extend(list(variable.parents))s

在 _back_grad_fn 中还需要注意两件事，1、我们需要将梯度添加到现有值，因为需要累积它们以防计算图中有多个路径到达该变量，2、还需要利用子节点的梯度，如果您想了解有关自动微分和矩阵微积分的更多详细信息，我们会在后续的文章中详细介绍。

神经网络模块

对于实际的神经网络模块，我们希望灵活地实现新的层和现有模块的重用。所以这里hi用PyTorch API 类似的架构，创建一个需要实现 init 和 forward 方法的基类 Module。除了这两个方法，我们还需要几个基于实用程序的方法来访问参数和子模块。

class Module(ABC):
    def __init__(self, training = True) -> None:
        self._parameters: List[Variable] = []
        self._modules: List[Module] = []
        self._training = training
        self._module_name = DEFAULT_MODULE_NAME

    @abstractmethod
    def forward(self, input: Variable) -> Variable:
        raise NotImplemented

    def add_parameter(self, parameter: Variable) -> Variable:
        self._parameters.append(parameter)
        return parameter

    def add_module(self, module: Module) -> Module:
        self._modules.append(module)
        return module

    def __call__(self, input: Variable) -> Variable:
        return self.forward(input)

    @property
    def modules(self) -> List[Module]:
        return self._modules

    @property
    def parameters(self) -> List[Variable]:
        modules_parameters = []
        modules = [self]
        visited_modules: Set[Module] = set([])

        while len(modules) != 0:
            module = modules.pop()

            if module in visited_modules:
                raise RecursionError("Module already visited, cycle detected.")

            modules_parameters.extend(module._parameters)
            modules.extend(module.modules)
            visited_modules.add(module)

        return modules_parameters

    def module_name(self) -> str:
        return self._module_name

线性层

线形层是神经网络模型中使用的最多，也是最简单的层，我们使用上一节中的抽象模块实现一个简单的线性层。线形层的数学运算非常简单：

我们将使用之前实现的变量来自动计算操作的实际结果和梯度，所以实现很简单：

class Linear(Module):
    def __init__(self, in_size, out_size) -> None:
        super().__init__()
        weights_data: np.ndarray = np.random.uniform(size=in_size * out_size).reshape((in_size, out_size))
        self.weights = Variable(weights_data, requires_grad=True)
        self.b = Variable(np.random.uniform(size=out_size), requires_grad=True)

        self.add_parameter(self.weights)
        self.add_parameter(self.b)

    def forward(self, input: Variable):
        tmp = input @ self.weights
        out = tmp + self.b
        return out

激活函数

现实世界中的大多数数据在自变量和因变量之间存在非线性关系，我们也希望我们的模型能够学习这种关系。如果我们不在线性层上添加非线性激活函数，那么无论我们添加多少线性层，最后我们都可以只用一层（一个权重矩阵）来表示它们。

所以这里实现最简单也是最常见的激活函数ReLu

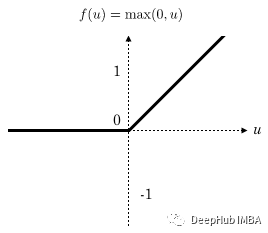
当实现 relu 函数时，还需要指定反向传播函数：

def relu(input: Variable) -> Variable:
    result = np.maximum(input.data, 0)
    variable = Variable(result, parents=(input,))

    if input.requires_grad:
        def _back_grad_fn():
            input.grad += np.transpose((variable.data > 0)) * variable.grad
        variable._back_grad_fn = _back_grad_fn
        variable.requires_grad = True

    return variable

优化器

在通过我们的模型执行前向传播并通过我们自定义的层进行梯度的反向传播之后，我们需要实际更新参数使损失函数变得更小。

最简单的优化器之一是 SGD（随机梯度下降），在本文的实现中，我们还是使用最简单的实现方法，仅使用梯度和学习率裁剪变化值增量并更新权重：

class BaseOptimizer(ABC):
    def __init__(self, parameters: List[Variable], lr=0.0001) -> None:
        super().__init__()
        self._parameters = parameters
        self._lr = lr

    def zero_grad(self):
        for parameter in self._parameters:
            if parameter.requires_grad == False:
                continue

            if isinstance(parameter.grad, np.ndarray):
                parameter.grad = np.zeros_like(parameter.grad)
            else:
                parameter.grad = np.array([0], dtype=np.float)

    @abstractmethod
    def step(self):
        raise NotImplementedError

class NaiveSGD(BaseOptimizer):
    def __init__(self, parameters: List[Variable], lr=0.001) -> None:
        super().__init__(parameters=parameters, lr=lr)

    def step(self):
        for parameter in self._parameters:
            clipped_grad = np.clip(parameter.grad, -1000, 1000)
            delta = -self._lr * clipped_grad
            delta = np.transpose(delta)
            parameter.data = parameter.data + delta

数据集

最后组件就是数据集了，数据集虽然并不是核心组件但是它却非常的重要，一位内它可以帮助我们组织数据集，并将其集成到训练过程中。我们也使用Pytorch的方法创建一个Dataset类，实现迭代器的dunder方法，并将特征X和标签Y转换为Variable类型:

class Dataset:
    def __init__(self, features: np.ndarray, labels: np.ndarray, batch_size=16) -> None:
        self._features = features
        self._labels = labels
        self._batch_size = batch_size
        self._cur_index = 0

    
    def __iter__(self):
        self._cur_index = 0
        return self

    def __next__(self) -> Tuple[Variable, Variable]:
        if self._cur_index >= len(self):
            raise StopIteration
        
        sample_batch, label_batch = self[self._cur_index]
        self._cur_index += self._batch_size
        
        return sample_batch, label_batch

    
    def __getitem__(self, idx) -> Tuple[Variable, Variable]:
        if idx >= len(self):
            raise IndexError

        sample_batch = Variable(self._features[self._cur_index: self._cur_index + self._batch_size])
        label_batch = Variable(self._labels[self._cur_index : self._cur_index + self._batch_size])

        return sample_batch, label_batch

    
    def __len__(self) -> int:
        return int(len(self._features) / self._batch_size)

训练

最后把所有东西放在一起，并使用 sklearn.datasets 使用人工生成的数据集训练一个简单的线性模型：

  X, y = datasets.make_regression(
        n_samples=100,
        n_features=1,
        n_informative=1,
        noise=10,
        coef=False,
        random_state=0
    )
    y = np.power(y, 2)

    dataset = Dataset(X, y, batch_size=1)
    return dataset
  
    optimizer = NaiveSGD(model.parameters, lr=config["lr"])
    training_loss = []

    for epoch in range(epochs):
        epoch_loss = .0

        for X, y in dataset:
            pred_y = model(X)

            loss = (pred_y - y) @ (pred_y - y)
            epoch_loss += loss.data.item()

            loss.backward()
            optimizer.step()
            optimizer.zero_grad()

        epoch_loss /= len(dataset)
        training_loss.append(epoch_loss)
        print(f"Epoch {epoch} | Loss: {epoch_loss}")

总结

就像开头说的那样本文所展示的实现绝不是生产级的并且非常有限，但是可以让我们更好地理解在其他流行框架的底层发生的一些操作，这是我们学习和使用深度学习框架必不可少的部分。

最后上面提到的gradflow代码地址如下：https://github.com/DACUS1995/gradflow，有兴趣的可以深入了解

作者：Tudor Surdoiu