【高阶数据结构】并查集的实现(含压缩路径)及其应用-C++版本

并查集原理

并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中

并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。常常在使用中以森林来表示

适合于描述这类问题的抽象数据类型称为并查集(union-findset)

小例子-编号和人

如果我们想让编号和人构成关系, 即可以通过编号找到对应的人,也可以通过人找到对应的编号怎么做?

template<classT>classUnionFindSet{public:UnionFindSet(const T* a, size_t n){for(int i =0; i < n; i++){
            _a.push_back(a[i]);
            _indexMap[a[i]]= i;}}private:
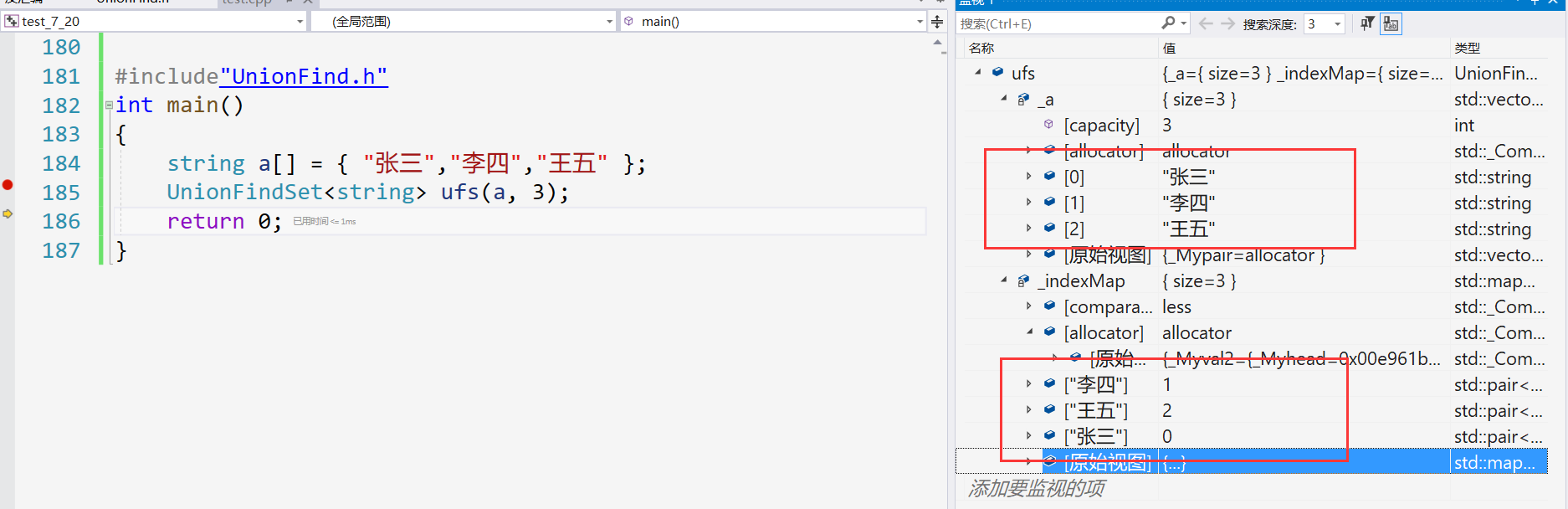
    vector<T> _a;//编号找人  下标对应的就是人名
    map<T,int> _indexMap;//人找编号  key:人名   value:编号};#include"UnionFind.h"intmain(){
    string a[]={"张三","李四","王五"};
    UnionFindSet<string>ufs(a,3);return0;}

并查集的实现

#include<iostream>#include<vector>classUnionFindSet{public:UnionFindSet(size_t n);
    size_t FindRoot(int x);voidUnion(int x1,int x2);boolInset(int x1,int x2);
    size_t SetCount();private:
    std::vector<int> _set;};

首先我们要知道如下规则:

1. 数组的下标对应集合中元素的编号
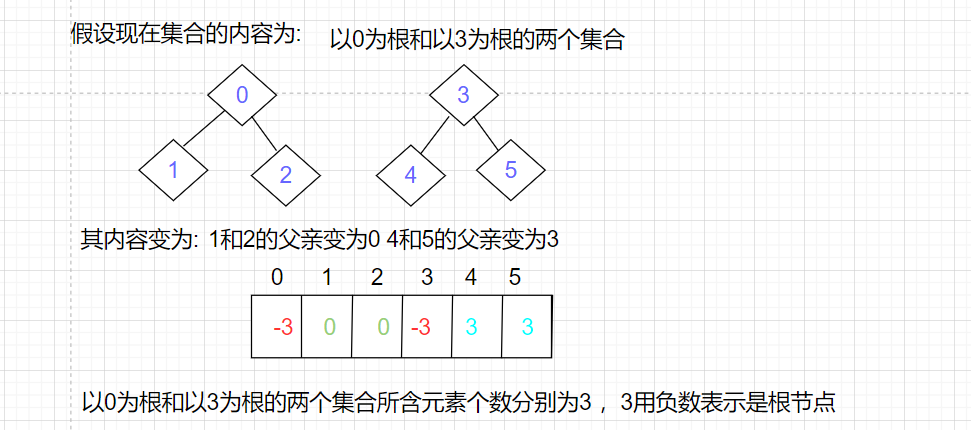
2. 数组中的值如果为负数，负号代表根，数字代表该集合中元素个数
3. 数组中的值如果为非负数，代表该元素双亲在数组中的下标

例如:

基本结构

classUnionFindSet{private:
    std::vector<int> _set;};

构造函数

最初每个元素各自构成一个集合, 初始状态就是-1,表示size个集合

UnionFindSet(int size):_set(size,-1)//size个元素都最初初始化为-1{}

查找根节点

返回根节点所在下标

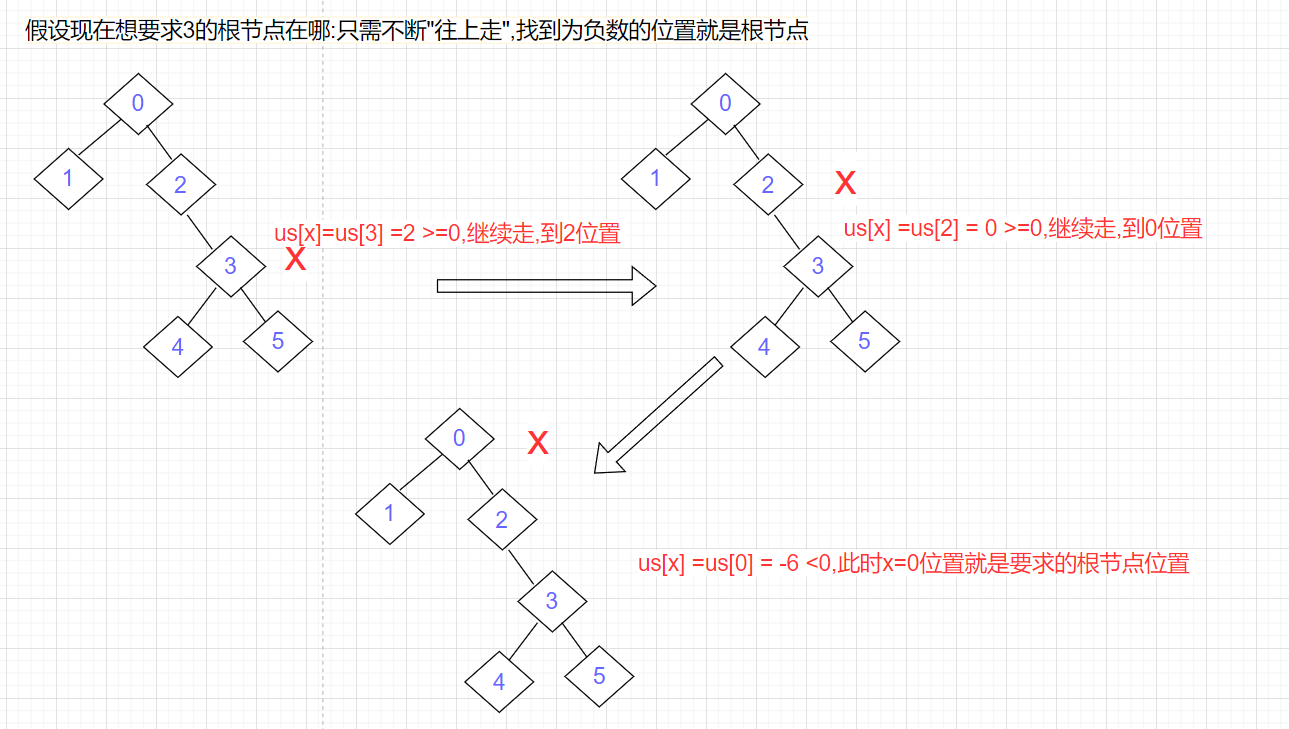
//如果_set[x]是负数,那么x就是某个集合的根//如果_set[x]不是负数,那么x的父亲节点就是_set[x]值对应的位置
size_t FindRoot(int x){while(_set[x]>=0){
        x = _set[x];}//来到这,_set[x] <0, 此时x就是根节点return x;}

路径压缩技巧

路径压缩实际上是在数据量太大的时候,访问一些数据可能在位于叶子位置,导致访问的效率不高

本质上我们查找的代表节点的时候,可以对该路径上的节点进行路径压缩

注意:最好不要用递归的时候进行路径压缩，因为路径深可能导致栈溢出

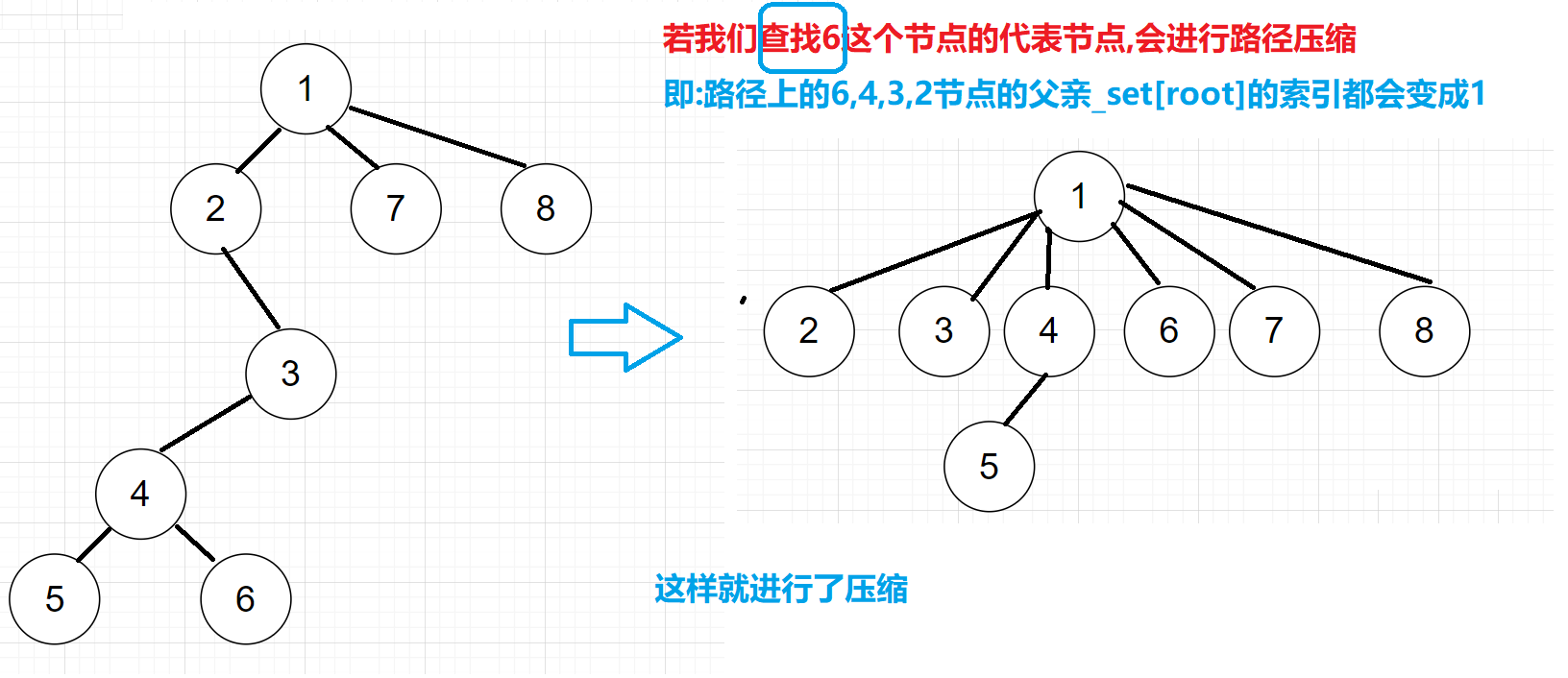
做法:

1)先找到当前路径节点的代表节点

2)然后从当前位置_set[x]开始的节点,沿途的节点的父亲位置都改为代表节点的位置

只需要根据下标关系往上迭代即可x节点的父亲位置就是_set[x]位置

注意:要提前保存x节点的父亲节点位置,因为更改当前位置的父亲节点, 会丢失以前的父亲节点

size_t FindRoot(int x){int root = x;while(_set[root]>=0){
        root = _set[root];}//此时root就是x这条路径的头节点(代表节点)//把沿途的节点的父亲都改为rootwhile(_set[x]>=0){int parent = _set[x];//先保存x节点的父节点位置
        _set[x]= root;//将x节点的父亲位置改为root位置
        x = parent;//往上迭代}return root;}

合并集合

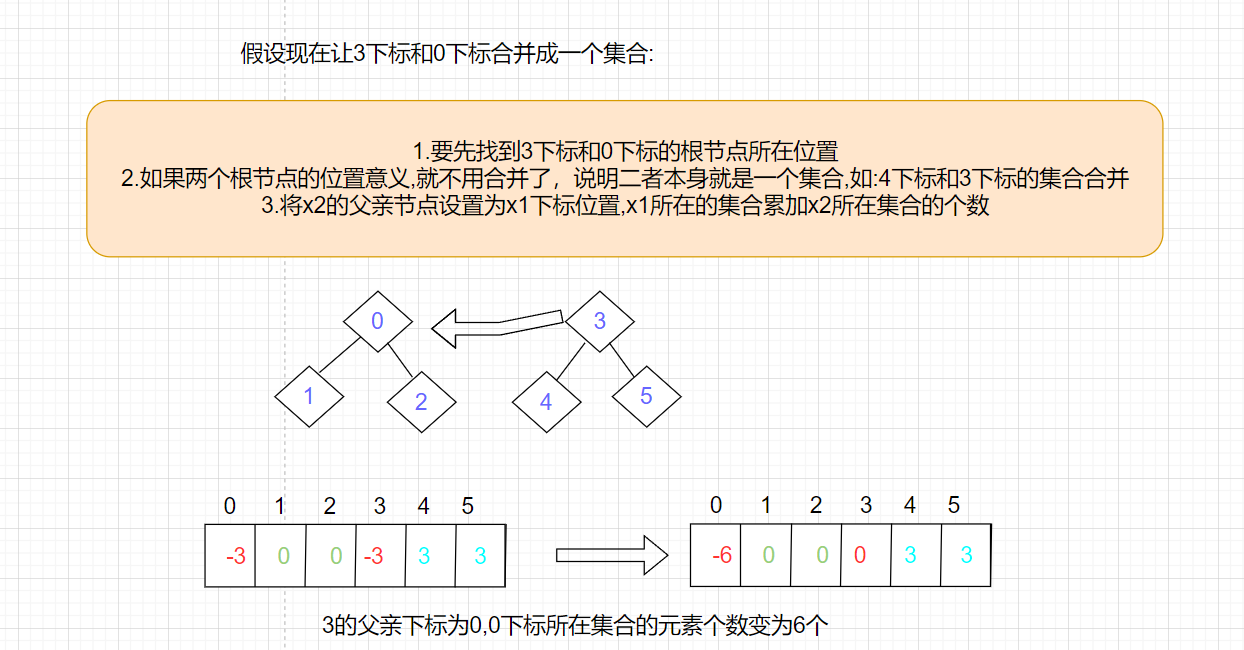
这里选择合并到x2所在的集合合并到x1所在的集合

voidUnion(int x1,int x2){//找到x1和x2的代表节点(根节点)
    size_t root1 =FindRoot(x1);
    size_t root2 =FindRoot(x2);//两个节点不在一个集合才合并//把root2合并到root1所在集合if(root1 != root2){
        _set[root1]+= _set[root2];//root2所在集合的元素累加到root1所在集合
        _set[root2]= root1;//root2的父亲变为root1}}

如果我们希望是小集合合并到大集合呢? 即元素少的集合合并到元素多的集合

路径压缩技巧

两颗树合并的时候,节点少的数往节点多的树合并

目的：为了使节点层数增多的节点相对减少

做法:

1)判断哪颗树的节点更多, 让root1变为是较大的集合, root2往root1合并

如何判断呢? 因为root1和root2是根,_set[root]的值是负数,代表该集合的元素个数, _set[root]值越大,集合元素个数越少

//x1和x2合并 ->本质是代表节点(根节点)合并voidUnion(int x1,int x2){//找到x1和x2的代表节点(根节点)
    size_t root1 =FindRoot(x1);
    size_t root2 =FindRoot(x2);//我们让root1的集合是大集合,小集合合并到大集合中//因为root1和root2是根,所以_set[root]的值为负数,代表集合的元素个数,值越小,元素越多if(_set[root1]> _set[root2])//说明root2集合元素多{::swap(root1, root2);}//两个节点不在一个集合才合并if(root1 != root2){
        _set[root1]+= _set[root2];//root2所在集合的元素累加到root1所在集合
        _set[root2]= root1;//root2的父亲变为root1}}

求集合个数

遍历_set,查看有多少元素是负数,就代表有多少个根节点, 即有多少个集合

size_t SetCount(){
    size_t count =0;for(auto e : _set){if(e <0) count++;}return count;}

判断两个元素是否在同一个集合

只需要判断两个元素的代表节点的位置是否相同即可

boolInset(int x1,int x2){returnFindRoot(x1)==FindRoot(x2);}

并查集的应用

省份数量

https://leetcode.cn/problems/number-of-provinces/

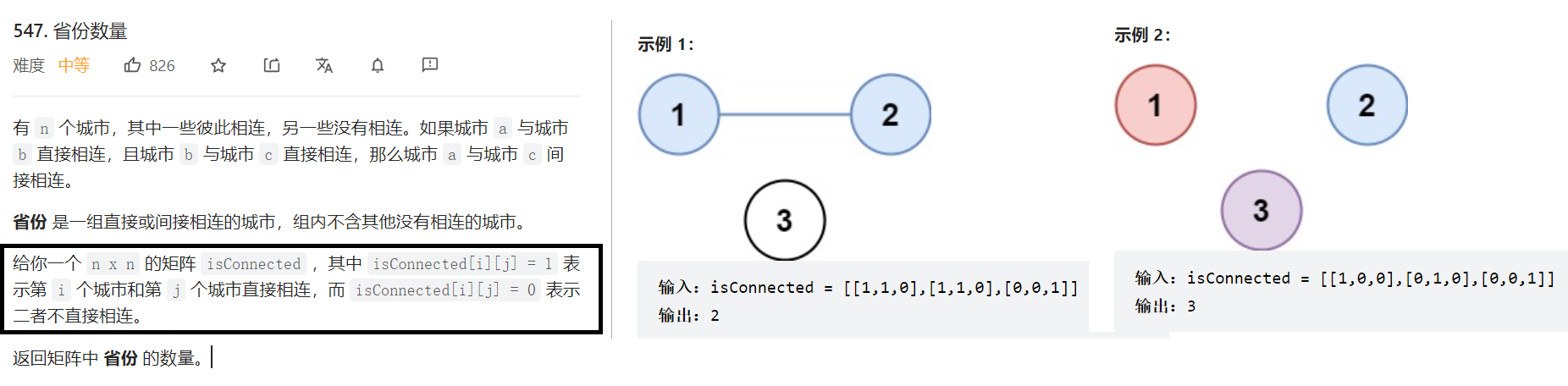
做法:遍历矩阵, 因为n[i][j] =1 表示第i城市和第j个城市相连 -> 所以我们可以把i和j合并到一个集合里面

遍历完成后,返回集合个数

classSolution{public:classUnionSet{public:UnionSet(size_t n =0){//最初自己就是一个集合
            us.resize(n,-1);//开辟n个空间,初始化为-1}//查找x对应的根节点下标intFindRoot(int x){//下标对应的值为负数的就是根节点//要保证x下标的合法性assert(x < us.size());while(us[x]>=0){
                x = us[x];}//退出循环时:us[x]<0,此时x下标就是对应的根节点return x;}//求集合个数->看us中有多少个元素是<0的intGetSize(){int count =0;for(auto& x : us){if(x <0) count++;}return count;}//小集合合并到大集合voidUnion(int x1,int x2){//要保证x1和x2下标的合法性assert(x1 < us.size());assert(x2 < us.size());//先找到二者对应的根节点所在下标int root1 =FindRoot(x1);int root2 =FindRoot(x2);//让root1是大集合的根//因为负数是表示元素个数,us[root1]>us[root2] 表示root2的集合元素个数比root1多if(us[root1]<us[root2]){swap(root1,root2);}//如果root1 == root2,说明x1和x2就是在一个集合中,不需要合并if(root1 != root2){//将root2所在集合的个数累加到root1中//root2的父亲的下标变为root1
                us[root1]+= us[root2];
                us[root2]= root1;}}private:
        vector<int> us;};intfindCircleNum(vector<vector<int>>& isConnected){//相连的省份他们都在一个集合里，所以只需要用并查集统计一共有几个集合即可int n = isConnected.size();//初始化每一个集合！ {0},{1},.....
        UnionSet us(n);//因为上下对称只需要考察上三角形即可for(int i =0;i<n;i++){for(int j = i+1;j<n;j++){//当前位置为1,就把j和i位置合并if(isConnected[i][j]==1){
                    us.Union(i,j);}}}//最后返回并查集中有多少个元素return us.GetSize();}};

当然,我们不必把整个并查集实现出来, 可以采取下面的方式做: 手动控制并查集

classSolution{public:intfindCircleNum(vector<vector<int>>& isConnected){
        vector<int>ufs(isConnected.size(),-1);//每个元素各为一个集合,初始化为-1//查找根节点 auto findRoot =[&ufs](int x)//Lamber表达式{while(ufs[x]>=0) 
                x = ufs[x];return x;};//遍历矩阵for(size_t i =0;i<isConnected.size();i++){for(size_t j =0;j<isConnected[i].size();j++){if(isConnected[i][j]==1){//合并集合int root1 =findRoot(i);int root2 =findRoot(j);if(root1 != root2)//合并到root1上{
                        ufs[root1]+= ufs[root2];
                        ufs[root2]= root1;}}}}//统计集合个数int count =0;for(auto e:ufs){if(e<0) count++;}return count;}};

等式方程的可满足性

https://leetcode.cn/problems/satisfiability-of-equality-equations/

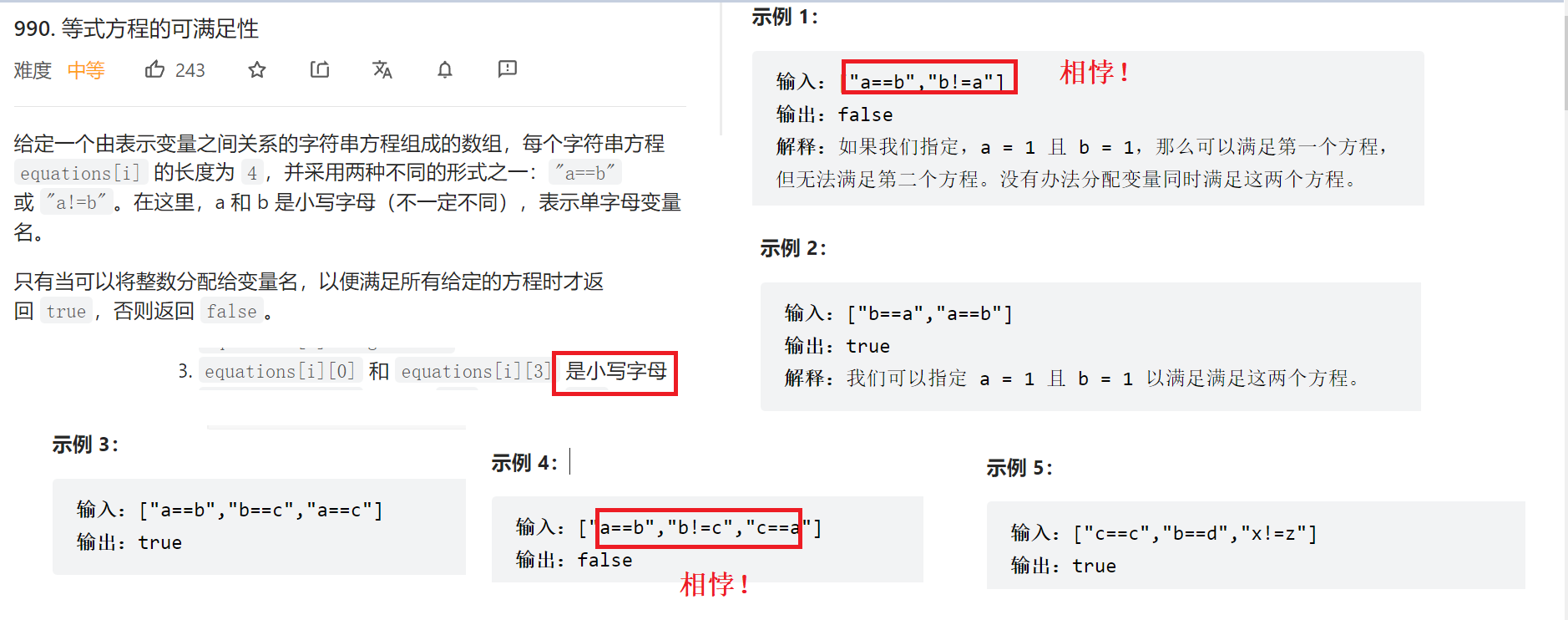
函数参数是:

vector<string>& equations

每一个元素是一条长度为4的方程

怎么做呢? 可以根据str[1]的字符判断这条方程是!= 还是 ==

• 相等的值放到一个集合中, 例如: a ==b b == c,那么a,b,c就在一个集合中！
• 不相等的值不能在一个集合中, 所以当我们遍历到 '！'字符时.判断左右两个字符是否在一个集合,如果在,就是相悖的,返回false!

方法:先遍历一遍字符串,把相等的值放到一个集合,然后再遍历一遍集合,看不相等的值是否在一个集合,如果在,就是相悖的,返回false 因为只有小写字母.所以可以只开辟26个空间进行映射!

等式左侧的字符str[0]映射为:

str[0] - 'a'

等式右侧的字符str[3]映射为:

str[3] - 'a'

classSolution{public:classUnionSet{public:UnionSet(size_t n =0){//最初自己就是一个集合
            us.resize(n,-1);//开辟n个空间,初始化为-1}//查找x对应的根节点下标intFindRoot(int x){//下标对应的值为负数的就是根节点//要保证x下标的合法性assert(x < us.size());while(us[x]>=0){
                x = us[x];}//退出循环时:us[x]<0,此时x下标就是对应的根节点return x;}//求集合个数->看us中有多少个元素是<0的intGetSize(){int count =0;for(auto& x : us){if(x <0) count++;}return count;}//将x2合并到x1voidUnion(int x1,int x2){//要保证x1和x2下标的合法性assert(x1 < us.size());assert(x2 < us.size());//先找到二者对应的根节点所在下标int root1 =FindRoot(x1);int root2 =FindRoot(x2);//如果root1 == root2,说明x1和x2就是在一个集合中,不需要合并if(root1 != root2){//将root2所在集合的个数累加到root1中//root2的父亲的下标变为root1
                us[root1]+= us[root2];
                us[root2]= root1;}}private:
        vector<int> us;};//如果两个字符相等，则放入同一个集合之中//如果两个字符不相等，它们应当在不同的集合中，此时查找它们所在集合的根//如果相同则说明这两个字符在同一个集合中，返回false。boolequationsPossible(vector<string>& equations){
        UnionSet us(26);//只有小写字母->开26个空间足矣//第一遍先把相等的值合并到一个集合for(auto& str:equations){if(str[1]=='='){
                us.Union(str[0]-'a',str[3]-'a');}}//第二遍把不相等的值判断在不在一个集合，如果在就逻辑相悖，返回falsefor(auto& str:equations){if(str[1]=='!'){if(us.FindRoot(str[0]-'a')==us.FindRoot(str[3]-'a')){returnfalse;}}}returntrue;}};

当然,我们不必把整个并查集实现出来, 可以采取下面的方式做: 手动控制并查集

classSolution{public:boolequationsPossible(vector<string>& equations){
         vector<int>ufs(26,-1);//只需要开26个空间映射auto findRoot =[&ufs](int x){while(ufs[x]>=0) 
                    x = ufs[x];return x;};//第一遍遍历,把相同的值合并到一个集合for(auto& str:equations){if(str[1]=='='){//合并两个集合int root1 =findRoot(str[0]-'a');//左字符的映射:str[0] -'a'int root2 =findRoot(str[3]-'a');//右字符的映射:str[3] -'a'if(root1 != root2){
                    ufs[root1]+= ufs[root2];
                    ufs[root2]= root1;}}}//第二遍遍历,判断不相等的是否在一个集合,如果在,就是相悖,返回falsefor(auto& str:equations){if(str[1]=='!'){//合并两个集合int root1 =findRoot(str[0]-'a');//左字符的映射:str[0] -'a'int root2 =findRoot(str[3]-'a');//右字符的映射:str[3] -'a'if(root1 == root2)//二者在一个集合中,相悖{returnfalse;}}}returntrue;//所有等式符合要求}};