【深度学习】SVM与百度飞桨

一.SVM和KNN的对比分析

  **前言**：SVM和KNN都是对**分类数据点进行距离的计算**，距离计算公式（二范数）是np.sqare (np.pow ( (x1-x2),2)),即根号下两点差的平方。

 SVM要比KNN分类效果一般要好，并且速度要快。

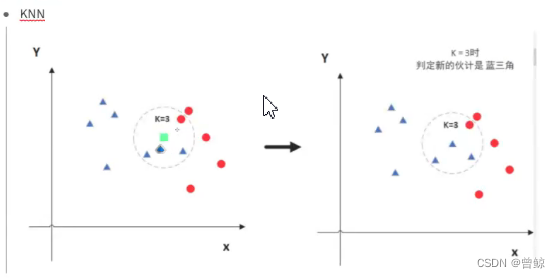
KNN的原理是 数量+临近，在范围内谁的数量多，那么未知的绿色方块就代指谁。

同样，SVM也是一种分类算法：

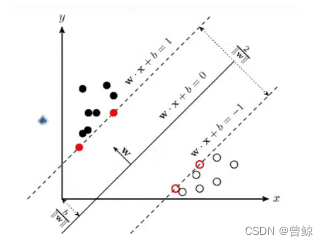
与KNN不同的是，其先分类，将所有数据划分不同区域，当随机未知数据降临上半部分，则其代表的是黑点，若在下面部分，则代表空心黑圈。

缺点则是计算相对较麻烦一些。

总结：

KNN分类问题，离哪些点较近，就归哪一类。

SVM分类问题，找决策边界，把数据进行划分开。

二.SVM原理梳理

1.首先是应用了向量的知识 (支持向量积)

将两组数据划分开，怎么样的决策边界才会更好呢？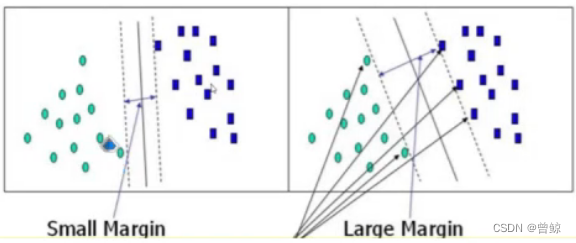

(1)支持向量是要大的，还是要小的？

要小的，要考虑离自己最近的雷才最安全。

(2)决策边界是要大的还是小的？

要大的，要最宽的道路才能行动的更快，更不容易踩雷。

2.部分数学原理 ：拉格朗日乘子法 → ·简化最终目标函数

3.软间隔优化

（1）即考虑一些异常的噪音，让分类更合理。（引入松弛因子）

（2）目标函数的变化，及c的引入（能够体现容错能力）
soft-margin

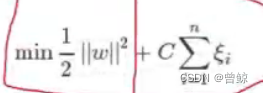
    新的目标函数：
           当C趋近于很大时：意味着分类严格不能有错误。
           当C趋近于很小时：意味着可以有更大的错误容忍 。

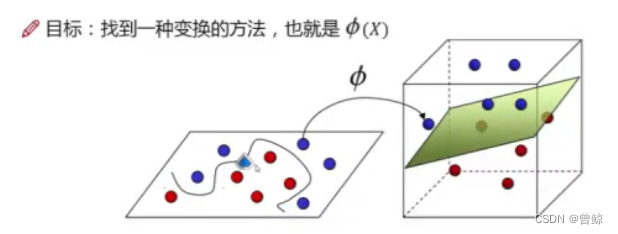
5.核函数（分类好的关键）

（1）升维，二位的变成三维的，可能能够很好的用平面分开。

     目标：找到一种变换的方法，也就是（X）。

6.相关案例

（1）鸢尾花案例

https://blog.csdn.net/RuDing/article/details/78008851

（2）案例扩展分析

https://blog.csdn.net/Kyrie_lrving/article/details/90404874

（3）复杂分析

https://blog.csdn.net/cxmscb/article/details/56277984

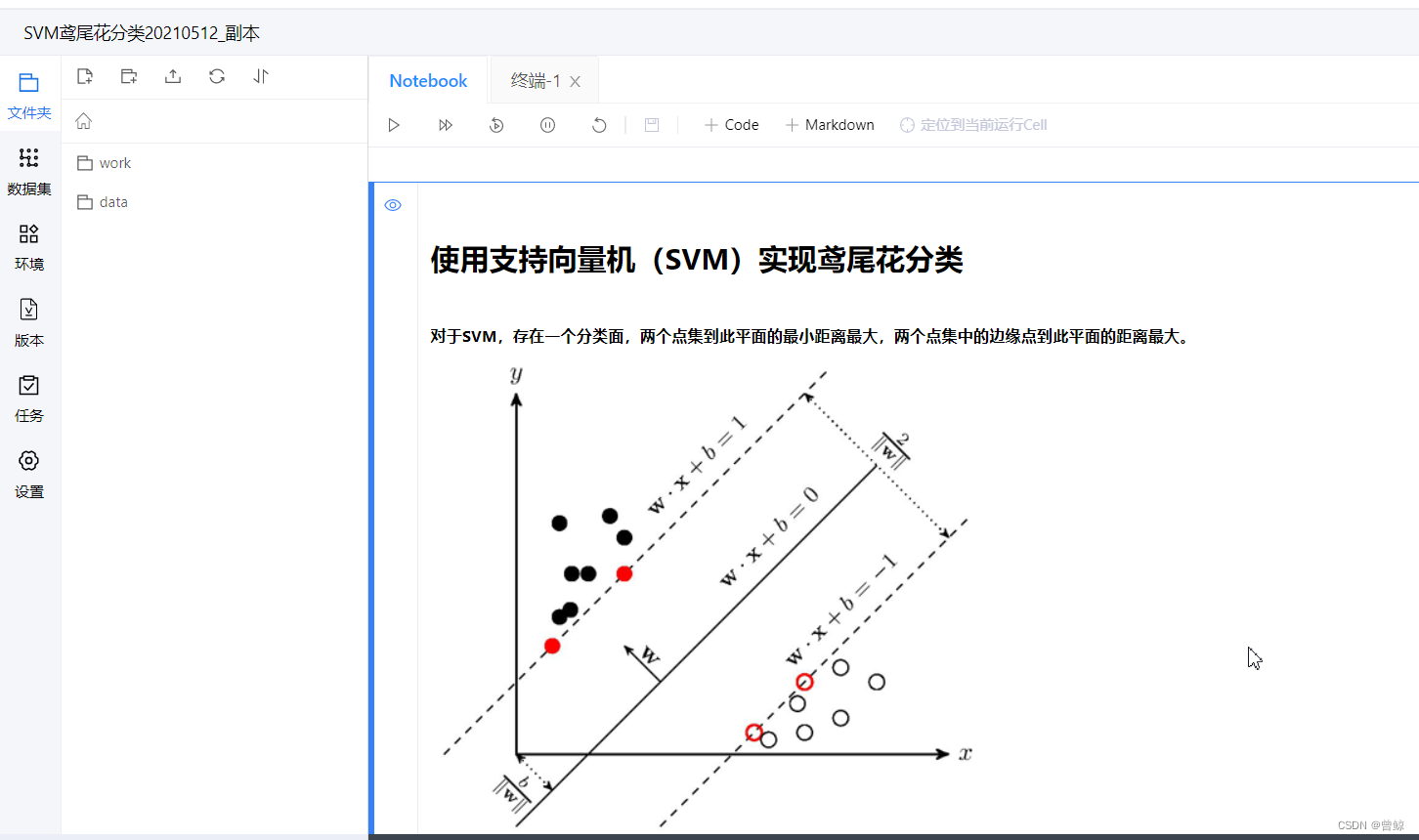
三.SVM代码在百度飞桨上实际运行