0
0

进阶C++__STL__容器vector使用方法【简单易懂】

vector容器

vector构造函数

  • vector<T> v; //采用模板实现类实现，默认构造函数
  • vector(v.begin(), v.end()); //将v[begin(), end())区间中的元素拷贝给本身。
  • vector(n, elem); //构造函数将n个elem拷贝给本身。
  • vector(const vector &vec); //拷贝构造函数。
#include<iostream>
#include<string> 
using namespace std;

#include <vector>

void printVector(vector<int>& v) {

    for (vector<int>::iterator it = v.begin(); it != v.end(); it++) {
        cout << *it << " ";
    }
    cout << endl;
}

void test01()
{
    vector<int> v1; //无参构造 默认构造 
    for (int i = 0; i < 10; i++)
    {
        v1.push_back(i);
    }
    printVector(v1);
    //通过区间方式构造 
    vector<int> v2(v1.begin(), v1.end());
    printVector(v2);
    // n个元素e方式构造 
    vector<int> v3(10, 0);
    printVector(v3);
    //拷贝构造 
    vector<int> v4(v3);
    printVector(v4);
}

int main() {

    test01();

    system("pause");

    return 0;
}

输出：

0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0

vector赋值操作

  • vector& operator=(const vector &vec);//重载等号操作符
  • assign(beg, end); //将[beg, end)区间中的数据拷贝赋值给本身。
  • assign(n, elem); //将n个elem拷贝赋值给本身。
#include<iostream>
#include<string> 
using namespace std;
#include <vector>

void printVector(vector<int>& v) {

    for (vector<int>::iterator it = v.begin(); it != v.end(); it++) {
        cout << *it << " ";
    }
    cout << endl;
}

//赋值操作
void test01()
{
    vector<int> v1; //无参构造
    for (int i = 0; i < 10; i++)
    {
        v1.push_back(i);
    }
    printVector(v1);

    vector<int>v2;
    v2 = v1;
    printVector(v2);

    vector<int>v3;
    v3.assign(v1.begin(), v1.end());
    printVector(v3);

    vector<int>v4;
    v4.assign(10, 100);
    printVector(v4);
}

int main() {

    test01();

    system("pause");

    return 0;
}

输出：

0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
100 100 100 100 100 100 100 100 100 100

vector容量和大小

  • empty(); //判断容器是否为空
  • capacity(); //容器的容量
  • size(); //返回容器中元素的个数
  • resize(int num); //重新指定容器的长度为num，若容器变长，则以默认值填充新位置。​ //如果容器变短，则末尾超出容器长度的元素被删除。
  • resize(int num, elem); //重新指定容器的长度为num，若容器变长，则以elem值填充新位置。​ //如果容器变短，则末尾超出容器长度的元素被删除
#include<iostream>
#include<string> 
using namespace std;
#include <vector>

void printVector(vector<int>& v) {

    for (vector<int>::iterator it = v.begin(); it != v.end(); it++) {
        cout << *it << " ";
    }
    cout << endl;
}

void test01()
{
    vector<int> v1;
    for (int i = 0; i < 10; i++)
    {
        v1.push_back(i);
    }
    printVector(v1);
    if (v1.empty())
    {
        cout << "v1为空" << endl;
    }
    else
    {
        cout << "v1不为空" << endl;
        cout << "v1的容量 = " << v1.capacity() << endl;
        cout << "v1的大小 = " << v1.size() << endl;
    }

    //resize 重新指定大小 ，若指定的更大，默认用0填充新位置，可以利用重载版本替换默认填充
    v1.resize(15,10);
    printVector(v1);

    //resize 重新指定大小 ，若指定的更小，超出部分元素被删除
    v1.resize(5);
    printVector(v1);
}

int main() {

    test01();

    system("pause");

    return 0;
}

vector插入和删除

  • push_back(ele); //尾部插入元素ele
  • pop_back(); //删除最后一个元素
  • insert(const_iterator pos, ele); //迭代器指向位置pos插入元素ele
  • insert(const_iterator pos, int count,ele);//迭代器指向位置pos插入count个元素ele
  • erase(const_iterator pos); //删除迭代器指向的元素
  • erase(const_iterator start, const_iterator end);//删除迭代器从start到end之间的元素
  • clear(); //删除容器中所有元素
#include<iostream>
#include<string> 
using namespace std;

#include <vector>

void printVector(vector<int>& v) {

    for (vector<int>::iterator it = v.begin(); it != v.end(); it++) {
        cout << *it << " ";
    }
    cout << endl;
}

//插入和删除
void test01()
{
    vector<int> v1;
    //尾插
    v1.push_back(10);
    v1.push_back(20);
    v1.push_back(30);
    v1.push_back(40);
    v1.push_back(50);
    printVector(v1);
    //尾删
    v1.pop_back();
    printVector(v1);
    //插入
    v1.insert(v1.begin(), 100);
    printVector(v1);

    v1.insert(v1.begin(), 2, 1000);
    printVector(v1);

    //删除
    v1.erase(v1.begin());
    printVector(v1);

    //清空
    v1.erase(v1.begin(), v1.end());
    v1.clear();
    printVector(v1);
}

int main() {

    test01();

    system("pause");

    return 0;
}

输出：

10 20 30 40 50
10 20 30 40
100 10 20 30 40
1000 1000 100 10 20 30 40
1000 100 10 20 30 40

vector数据存取

  • at(int idx); //返回索引idx所指的数据
  • operator[]; //返回索引idx所指的数据
  • front(); //返回容器中第一个数据元素
  • back(); //返回容器中最后一个数据元素
#include<iostream>
#include<string> 
using namespace std;
#include <vector>

void test01()
{
    vector<int>v1;
    for (int i = 0; i < 10; i++)
    {
        v1.push_back(i);
    }

    for (int i = 0; i < v1.size(); i++)
    {
        cout << v1[i] << " ";
    }
    cout << endl;

    for (int i = 0; i < v1.size(); i++)
    {
        cout << v1.at(i) << " ";
    }
    cout << endl;

    cout << "v1的第一个元素为： " << v1.front() << endl;
    cout << "v1的最后一个元素为： " << v1.back() << endl;
}

int main() {

    test01();

    system("pause");

    return 0;
}

输出：

0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
v1的第一个元素为： 0
v1的最后一个元素为： 9

vector互换容器

  • swap(vec); // 将vec与本身的元素互换
#include<iostream>
#include<string> 
using namespace std;
#include <vector>

void printVector(vector<int>& v) {

    for (vector<int>::iterator it = v.begin(); it != v.end(); it++) {
        cout << *it << " ";
    }
    cout << endl;
}

void test01()
{
    vector<int>v1;
    for (int i = 0; i < 10; i++)
    {
        v1.push_back(i);
    }
    printVector(v1);

    vector<int>v2;
    for (int i = 10; i > 0; i--)
    {
        v2.push_back(i);
    }
    printVector(v2);

    //互换容器
    cout << "互换后" << endl;
    v1.swap(v2);
    printVector(v1);
    printVector(v2);
}

void test02()
{
    vector<int> v;
    for (int i = 0; i < 100000; i++) {
        v.push_back(i);
    }

    cout << "v的容量为：" << v.capacity() << endl;
    cout << "v的大小为：" << v.size() << endl;

    v.resize(3);

    cout << "v的容量为：" << v.capacity() << endl;
    cout << "v的大小为：" << v.size() << endl;

    //收缩内存
    vector<int>(v).swap(v); //匿名对象

    cout << "v的容量为：" << v.capacity() << endl;
    cout << "v的大小为：" << v.size() << endl;
}

int main() {

    test01();

    test02();

    system("pause");

    return 0;
}

输出：

0 1 2 3 4 5 6 7 8 9
10 9 8 7 6 5 4 3 2 1
互换后
10 9 8 7 6 5 4 3 2 1
0 1 2 3 4 5 6 7 8 9
v的容量为：131072
v的大小为：100000
v的容量为：131072
v的大小为：3
v的容量为：3
v的大小为：3

总结：swap可以使两个容器互换，可以达到实用的收缩内存效果

vector预留空间

reserve(int len);

//容器预留len个元素长度，预留位置不初始化，元素不可访问。

vector开辟空间原理：

当空间不够时，会重新开辟一块更大的空间，将原来空间内容拷贝到这个更大的空间，并指向这块空间；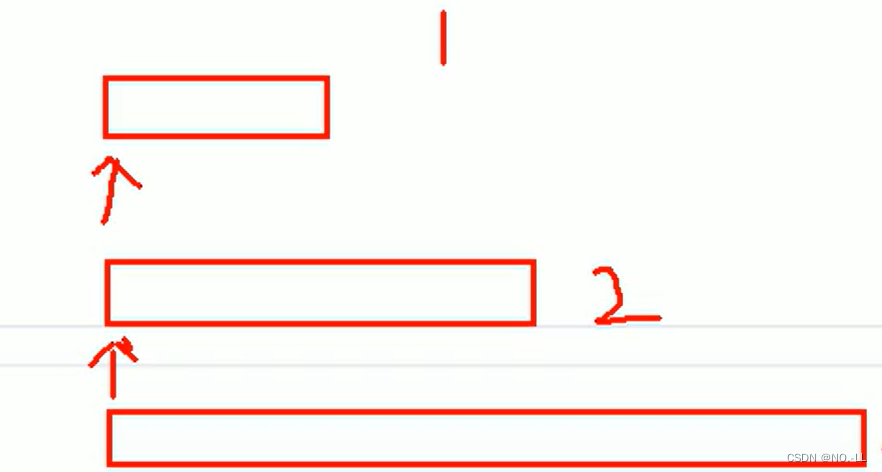

#include<iostream>
#include<string> 
using namespace std;
#include <vector>

void test01()
{
    vector<int> v;

    //预留空间
    //v.reserve(100000);

    int num = 0;
    int* p = NULL;
    for (int i = 0; i < 100000; i++) {
        v.push_back(i);
        if (p != &v[0]) {
            p = &v[0];
            num++;
        }
    }

    cout << "num:" << num << endl;
}

int main() {

    test01();
    
    system("pause");

    return 0;
}

输出：（不同编译器结果不同）

num:18

利用开辟空间原理判断指向的地址是否改变，我们发现vector存100000个元素时要改变18次，即重新开辟并拷贝18次；这样非常耗费时间；

当我们使用reserve直接预留100000空间时，则只需要一次，非常节约时间

reserve（）的实现

/* reserve */
void reserve(size_t new_capacity) {
    if (new_capacity > capacity()) {              // 检查是否真的需要扩容
        if (_finish == _eos) {
            size_t sz = size();   // 提前把size算好
 
            T* tmp = new T[new_capacity];
            if (_start) {
                // memcpy(tmp, _start, sizeof(T) * size());   有问题！
 
                    //自己把原空间的数据拷贝到新空间
                for (size_t i = 0; i < sz; i++) { 
                    // 如果T是int，一个一个拷贝没问题
                    // 如果T是string等自定义问题，一个一个拷贝调用的是T的深拷贝，也不会出问题。
                    tmp[i] = _start[i];  
                }
                    
                delete[] _start;                          // 并释放原有的旧空间
            }
 
            _start = tmp;                    // 指向新空间
            _finish = tmp + sz;                 // 现场算size() 会有问题，因为start已经被更新成tmp了
            _eos = _start + new_capacity;
        }
    }
}

vector的增删查改的模拟实现

函数接口：

namespace bit

{

  template<class T>

  class vector

  {

  public:

    // Vector的迭代器是一个原生指针

    typedef T* iterator；

    typedef const T* const_iterator；

    iterator begin()；

    iterator end()；

    const_iterator cbegin()；

    const_iterator cend() const；

    // construct and destroy

    vector()；

    vector(int n, const T& value = T())；

    template<class InputIterator>

    vector(InputIterator first, InputIterator last)；

    vector(const vector<T>& v)；

    vector<T>& operator= (vector<T> v)；

    ~vector()；

    // capacity

    size_t size() const ；

    size_t capacity() const；

    void reserve(size_t n)；

    void resize(size_t n, const T& value = T())；

    ///access///

    T& operator[](size_t pos)；

    const T& operator[](size_t pos)const；

    ///modify/

    void push_back(const T& x)；

    void pop_back()；

    void swap(vector<T>& v)；

    iterator insert(iterator pos, const T& x)；

    iterator erase(Iterator pos)；

  private:

    iterator _start; // 指向数据块的开始

    iterator _finish; // 指向有效数据的尾

    iterator _endOfStorage; // 指向存储容量的尾

  };

}

模拟实现

namespace bit
{
  template<class T>
  class vector
  {
  public:
    // Vector的迭代器是一个原生指针

    typedef T* iterator；

    typedef const T* const_iterator；

    iterator begin()
    {
      return _start;
    }
    iterator end()
    {
      return _finish;
    }
    const_iterator cbegin()const
    {
      return _start;
    }
    const_iterator cend() const
    {
      return _finish;
    }

    // construct and destroy
    vector(): _start(nullptr), _finish(nullptr), _endOfStorage(nullptr)
    {}
    vector(int n, const T& value = T())
      : _start(nullptr), _finish(nullptr),_endOfStorage(nullptr)
    {
      reserve(n);
      while (n--)
      {
        push_back(value);
      }
    }

    template<class InputIterator>

    vector(InputIterator first, InputIterator last)
    {
      reserve(last - first);
      while (first != last)
      {
        push_back(*first);
        ++first;
      }
    }

    vector(const vector<T>& v)
      : _start(nullptr), _finish(nullptr), _endOfStorage(nullptr)
    {
      reserve(v.capacity());
      iterator it = begin();
      const_iterator vit = v.cbegin();
      while (vit != v.cend())
      {
       *it++ = *vit++;
      }
      _finish = _start + v.size();
      _endOfStorage = _start + v.capacity();
    }

    vector<T>& operator= (vector<T> v)
    {
      swap(v);
      return *this;
    }

    ~vector()
    {
      delete[] _start;
      _start = _finish = _endOfStorage = nullptr;
    }

    // capacity
    size_t size() const 
    {
      return _finish - _start;
    }

    size_t capacity() const
    {
      return _endOfStorage - _start;
    }

    void reserve(size_t n)
    {

      if (n > capacity())
      {
        size_t oldSize = size();
        T* tmp = new T[n];
        if (_start)
        {
          for (size_t i = 0; i < oldSize; ++i)
          tmp[i] = _start[i];
        }
        _start = tmp;
        _finish = _start + size;
        _endOfStorage = _start + n;
      }

    }

    void resize(size_t n, const T& value = T())
    {
      // 1.如果n小于当前的size，则数据个数缩小到n
      if (n <= size())
      {
        _finish = _start + n;
        return;
      }

      // 2.空间不够则增容
      if (n > capacity())
       reserve(n);

      // 3.将size扩大到n
      iterator it = _finish;
      iterator _finish = _start + n;
      while (it != _finish)
      {
        *it = value;
        ++it;
      }
    }

    ///access///

    T& operator[](size_t pos)
    {
      return _start[pos];
    }

    const T& operator[](size_t pos)const
    {
      return _start[pos];
    }

    ///modify/

    void push_back(const T& x)
    {
      insert(end(), x);
    }

    void pop_back()
    {
      erase(--end());
    }

    void swap(vector<T>& v)
    {
      swap(_start, v._start);
      swap(_finish, v._finish);
      swap(_endOfStorage, v._endOfStorage);
    }

    iterator insert(iterator pos, const T& x)
    {
      assert(pos <= _finish);

      // 空间不够先进行增容
      if (_finish == _endOfStorage)
      {
        size_t size = size();
        size_t newCapacity = (0 == capacity())? 1 : capacity() * 2;
        reserve(newCapacity);

        // 如果发生了增容，需要重置pos
        pos = _start + size;
      }

      iterator end = _finish - 1;
      while (end >= pos)
      {
        *(end + 1) = *end;
        --end;
      }
      *pos = x;
      ++_finish;
      return pos;
    }

    // 返回删除数据的下一个数据

// 方便解决:一边遍历一边删除的迭代器失效问题

    iterator erase(Iterator pos)
    {
      // 挪动数据进行删除
      iterator begin = pos + 1;
      while (begin != _finish) 
      {
        *(begin - 1) = *begin;
        ++begin;
      }
      --_finish;
      return pos;
    }
  private:
    iterator _start; // 指向数据块的开始
    iterator _finish; // 指向有效数据的尾
    iterator _endOfStorage; // 指向存储容量的尾

  };

}

经典题目练习

1.杨辉三角OJ

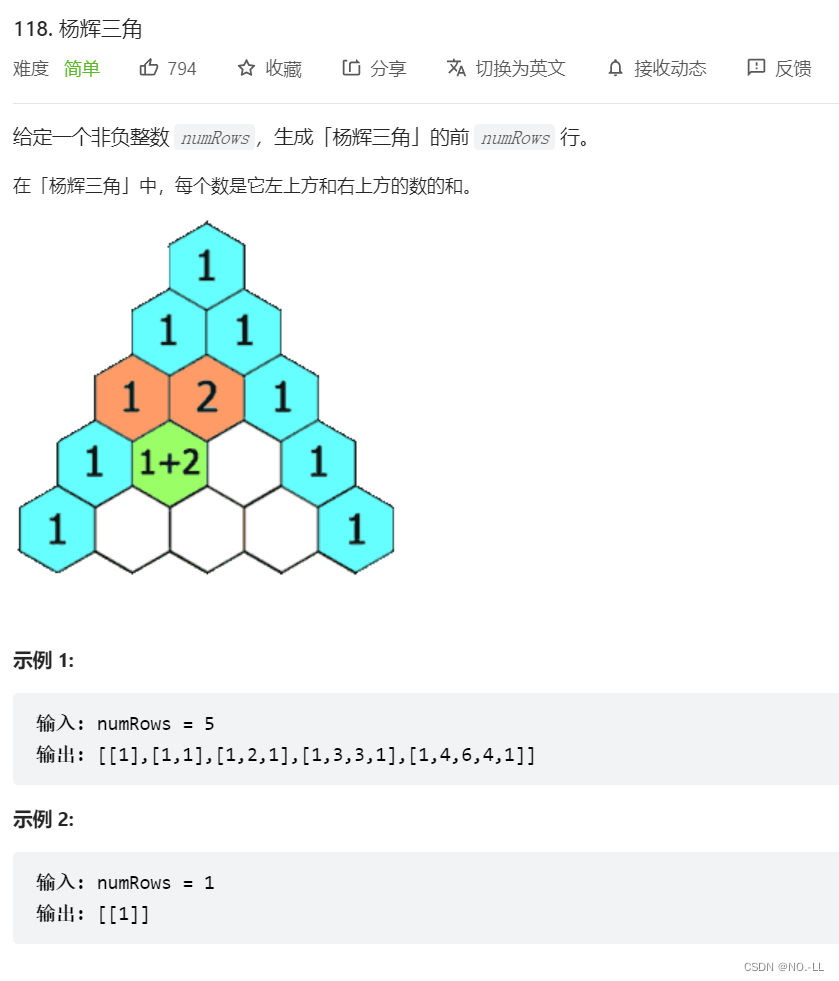
模拟；练一练二维vector 

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> vv;
        vv.resize(numRows);
        for(size_t i=1;i<=numRows;i++)
        {
            vv[i-1].resize(i,0);

            vv[i-1][0]=1;
            vv[i-1][i-1]=1;
        }

        for(int i=0;i<vv.size();i++)
        {
            for(int j=0;j<vv[i].size();j++){
                if(vv[i][j]==0)
                {
                    vv[i][j]=vv[i-1][j]+vv[i-1][j-1];
                }
            }
        }
        return vv;
    }
};

2.删除排序数组中的重复项 OJ

快慢指针：

所谓快：不加条件判断的数组下标累计
所谓慢：加上条件判断的数组下标累计

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int n=nums.size();
        if(n==0){
            return 0;
        }
        int fast=1,slow=1;
        while(fast<n)
        {
            if(nums[fast]!=nums[fast-1]){
                nums[slow]=nums[fast];
                slow++;
            }
            fast++;
        }
        return slow;
    }
};

3. 数组中出现次数超过一半的数字

**最优解：候选法 **

思想就是：如果两个数不相等，就消去这两个数，最坏情况下，每次消去一个众数和一个非众数，那么如果存在众数，最后留下的数肯定是众数（因为超过数组一半）。

  1. 假设cond为候选人，cnt为票数（要找到票最多的当选）；
  2. 如果cnt为0，说明没有候选人或者该候选人票不够选不了；
  3. 否则，如果cnt > 0, 表示有候选人，如果当前数=cond，则++cnt，否则--cnt
class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        int cond = 0;
        int cnt = 0;
        for (int i=0; i<numbers.size(); ++i) 
        {
            if (cnt == 0) 
            {
                cond = numbers[i];
                ++cnt;
            }
            else
            {
                if (cond == numbers[i]) ++cnt;
                else --cnt;
            }
        }
        return cond;
    }
};

4.只出现一次的数字

不需要额外空间的方法，就往位运算上想

  1. 交换律：a ^ b ^ c <=> a ^ c ^ b
  2. 任何数于0异或为任何数 0 ^ n => n
  3. 相同的数异或为0: n ^ n => 0
class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ret=0;
        for(auto e:nums)
            ret^=e;
        return ret;
    }
};

5.电话号码字母组合

思路：

由题意知就是把字母一一组合；

  1. 首先使用哈希表存储每个数字对应的所有可能的字母，然后进行回溯操作
  2. 假设输入“234”，进入递归，首先获得str第一个字符‘2’然后转成数字，取数字映射的字符串
  3. 开始遍历字符“abc”，刚取到‘a’时再进入递归取第二个字符‘3’，取数字映射的字符串“def”后开始遍历，以此类推我们的combineStr为“adg”
  4. 取到“adg”时就到顶了，利用di==digits.size()判断，将取到的组合数保存到retV并开始回溯；
  5. 由auto ch : str 我们会遍历“ghi”，按照上述同理方法得到“adh”,“adi”，然后回溯到第二次取‘e’，同理得“aeg”，“aeh”，“aei”
  6. 最终取到333种排列

回溯算法用于寻找所有的可行解，如果发现一个解不可行，则会舍弃不可行的解。在这道题中，由于每个数字对应的每个字母都可能进入字母组合，因此不存在不可行的解，直接穷举所有的解即可。

class Solution {
    string nums[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public:
    void Combine(string digits,int di,string combineStr,vector<string>& retV)
    {
        if(di==digits.size())
        {
            retV.push_back(combineStr);
            return;
        }
        int num=digits[di]-'0';
        string str=nums[num];

        for(auto ch:str)
        {
            Combine(digits,di+1,combineStr+ch,retV);
        }
    }
    vector<string> letterCombinations(string digits) {
        vector<string> retV;
        if(digits.empty())
            return retV;
        int i=0;
        string str;
        Combine(digits,i,str,retV);
        return retV;
    }
};

6. 连续子数组的最大和

经典动态规划

  • step 1：可以用dp数组表示以下标iii为终点的最大连续子数组和。
  • step 2：遍历数组，每次遇到一个新的数组元素，连续的子数组要么加上变得更大，要么这个元素本身就更大，要么会更小，更小我们就舍弃，因此状态转移为dp[i]=max(dp[i−1]+array[i],array[i])dp[i] = max(dp[i - 1] + array[i], array[i])dp[i]=max(dp[i−1]+array[i],array[i])。
  • step 3：因为连续数组可能会断掉，每一段只能得到该段最大值，因此我们需要维护一个最大值。
class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        vector<int> dp(array.size(),0);
        dp[0]=array[0];
        int maxv=dp[0];
        for(int i=1;i<array.size();i++)
        {
            dp[i]=max(dp[i-1]+array[i],array[i]);
            maxv=max(maxv,dp[i]);
        }
        return maxv;
    }
};
标签： c++ 算法 开发语言
本文转载自: https://blog.csdn.net/qq_61386381/article/details/125869840
版权归原作者 NO.-LL 所有， 如有侵权，请联系我们删除。
登录后发布评论

“进阶C++__STL__容器vector使用方法【简单易懂】”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

零基础5分钟上手谷歌云GCP - 服务器自动扩展

Linux中使用Docker容器构建Tomcat容器完整教程

【每天学会一个渗透测试工具】SQLmap安装教程及使用

真正的IDEA在线版有多好用

【Linux 】开发利器：深度探索 Vim 编辑器的无限可能

vue路由和路由安装

基于Java+SpringBoot+Vue+MySQL的智能菜谱推荐管理系统

文章导航