Fast-Planner(一)前端详解kinodynamic A*

作为无人机自主运动的入门路径规划算法，详细表述了路径规划的前端和后端，前端为路径搜索，后端未路径优化。具体参考代码。

一、kinodynamic a_star 路径搜索

这里参考的文章是Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments
总的可以概括为融合动力学约束的A*搜索，通过共轭梯度下降求局部最优。

解析kinodynamic_astar.cpp

Pathnode类(文章中motion Primitives)反向链表

classPathNode{public:/* -------------------- */
  Eigen::Vector3i index;//voxel坐标
  Eigen::Matrix<double,6,1> state;//基元状态,分别为xyz及其一阶导(vel)double g_score, f_score;//代价函数、启发函数
  Eigen::Vector3d input;//输入，分别为xyz上的二阶导(acc)double duration;//输入持续时间double time;// dynint time_idx;
  PathNode* parent;//父节点char node_state;/* -------------------- */PathNode(){
    parent =NULL;
    node_state = NOT_EXPAND;}~PathNode(){};
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW
};typedef PathNode* PathNodePtr;

主函数

/*
  kinodynamic A*的主函数
    parameter：
      - start_pt：起点位置
      - start_v: 起始速度
      - start_a: 起始加速度
      - end_pt:  终点位置
      - end_v:   终点速度
      - init：   初始化成功标志位
      - dynamic：动静规划标志位
      - time_start:起始时间
*/intKinodynamicAstar::search(Eigen::Vector3d start_pt, Eigen::Vector3d start_v, Eigen::Vector3d start_a,
                             Eigen::Vector3d end_pt, Eigen::Vector3d end_v,bool init,bool dynamic,double time_start)

读取传入参数

//读取传入参数
  start_vel_ = start_v;
  start_acc_ = start_a;

  PathNodePtr cur_node = path_node_pool_[0];//取出第一个路径点赋给当前节点
  cur_node->parent =NULL;//父节点
  cur_node->state.head(3)= start_pt;
  cur_node->state.tail(3)= start_v;
  cur_node->index =posToIndex(start_pt);//获得全局坐标系下的位置索引
  cur_node->g_score =0.0;//记录当前成本代价

  Eigen::VectorXd end_state(6);
  Eigen::Vector3i end_index;double time_to_goal;//路径规划时间

  end_state.head(3)= end_pt;
  end_state.tail(3)= end_v;
  end_index =posToIndex(end_pt);
  cur_node->f_score = lambda_heu_ *estimateHeuristic(cur_node->state, end_state, time_to_goal);//计算启发函数
  cur_node->node_state = IN_OPEN_SET;//标记为OPEN
  open_set_.push(cur_node);//将该点放入OPEN集，即论文中的C
  use_node_num_ +=1;//扩展点数计数

启发函数

该文利用Pontryagins minimum principle计算从Xc到Xg轨迹的启发函数。笔者根据自身能力进行推导，具体参考A Computationally Efficient Motion Primitive for Quadrocopter Trajectory Generation及D. P. Bertsekas的《动态规划和最优控制》。
3D运动的cost function，Jk为投影到三轴上的加加速度

状态：

      S 
     
    
      k 
     
    
   
     = 
    
   
     ( 
    
    
    
      p 
     
    
      k 
     
    
   
     , 
    
    
    
      v 
     
    
      k 
     
    
   
     , 
    
    
    
      a 
     
    
      k 
     
    
   
     ) 
    
   
  
    S_k=(p_k,v_k,a_k) 
   
  
Sk​=(pk​,vk​,ak​)

状态方程：

       S 
      
     
       ˙ 
      
     
    
      k 
     
    
   
     = 
    
    
    
      f 
     
    
      s 
     
    
   
     ( 
    
    
    
      S 
     
    
      k 
     
    
   
     , 
    
    
    
      j 
     
    
      k 
     
    
   
     ) 
    
   
     = 
    
   
     ( 
    
    
    
      v 
     
    
      k 
     
    
   
     , 
    
    
    
      a 
     
    
      k 
     
    
   
     , 
    
    
    
      j 
     
    
      k 
     
    
   
     ) 
    
   
  
    \dot{S}_k=f_s(S_k,j_k)=(v_k,a_k,j_k) 
   
  
S˙k​=fs​(Sk​,jk​)=(vk​,ak​,jk​)

构建Hamiltonian函数和协态方程：

求解costate的微分方程得

最佳输入轨迹J*(t)通过求最小化Hamiltonian函数(PMP原理)获得，即

j*(t)为加加速度的轨迹，

      S 
     
    
      0 
     
    
   
     = 
    
   
     ( 
    
    
    
      p 
     
    
      0 
     
    
   
     , 
    
    
    
      v 
     
    
      0 
     
    
   
     , 
    
    
    
      a 
     
    
      0 
     
    
   
     ) 
    
   
  
    S_0=(p_0,v_0,a_0) 
   
  
S0​=(p0​,v0​,a0​)通过积分可以获 
 
  
   
    
    
      a 
     
    
      ∗ 
     
    
   
     ( 
    
   
     t 
    
   
     ) 
    
   
     , 
    
    
    
      v 
     
    
      ∗ 
     
    
   
     ( 
    
   
     t 
    
   
     ) 
    
   
     , 
    
   
     p 
    
   
     ∗ 
    
   
     ( 
    
   
     t 
    
   
     ) 
    
   
  
    a^*(t),v^*(t),p*(t) 
   
  
a∗(t),v∗(t),p∗(t)

目标状态

      S 
     
    
      f 
     
    
   
     = 
    
   
     ( 
    
    
    
      p 
     
    
      f 
     
    
   
     , 
    
    
    
      v 
     
    
      f 
     
    
   
     , 
    
    
    
      a 
     
    
      f 
     
    
   
     ) 
    
   
  
    S_f=(p_f,v_f,a_f) 
   
  
Sf​=(pf​,vf​,af​)，

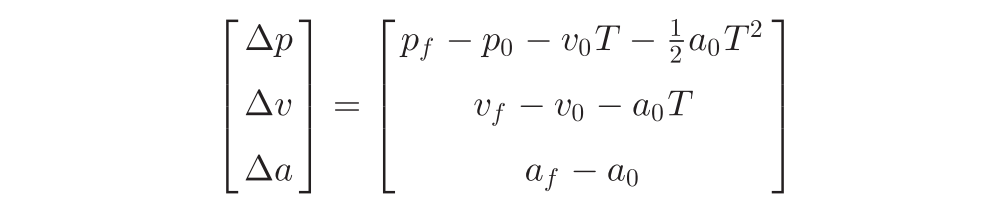
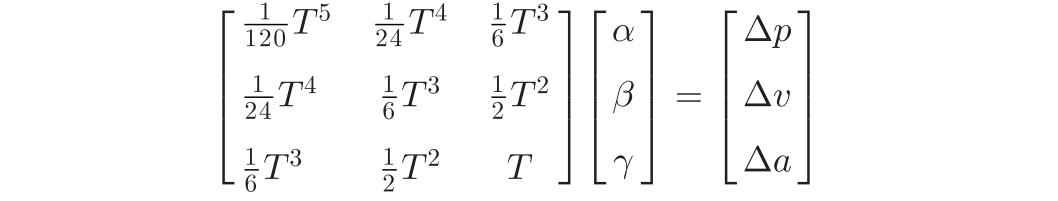
解得：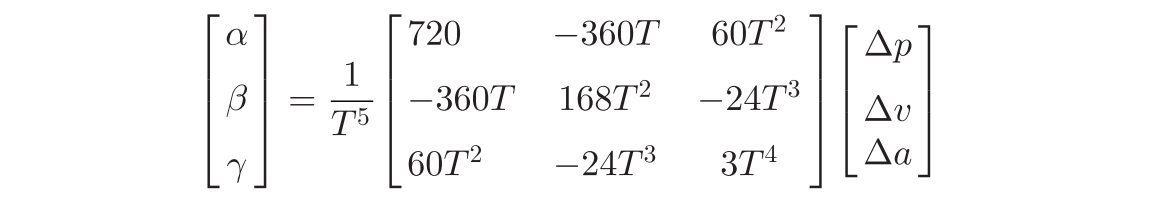


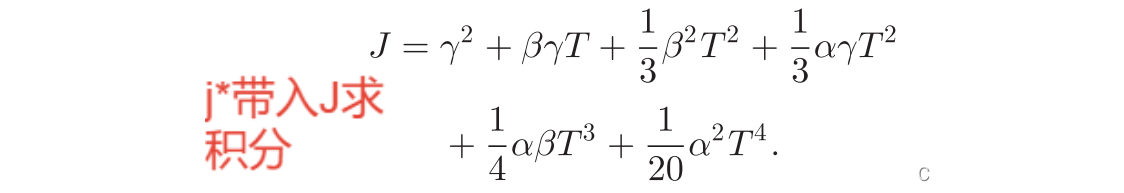
FAST-Planner当中最小化加速度，故与上述最小化加加速度不同，文中给出的公式如下：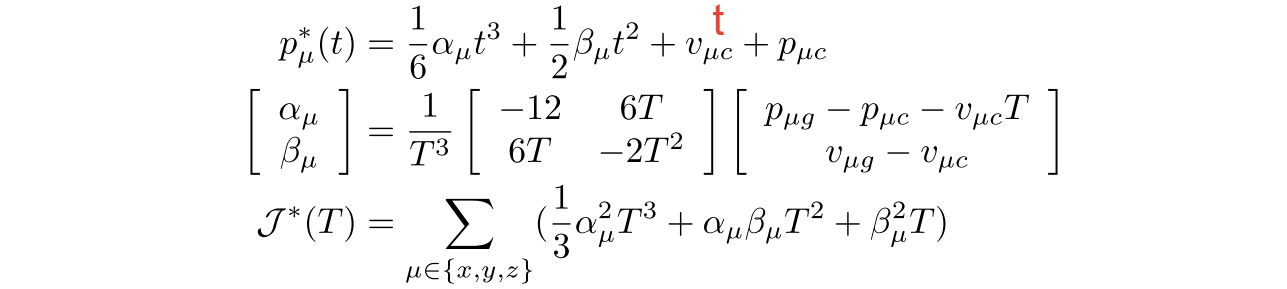

启发函数代码(即上述使J取最小的T)：

/*
  计算启发函数
    parameters：
      - x1,x2:起点和终点状态
      - optimal_time:达到最终点的最优时间
    return:
      - 代价值
*/doubleKinodynamicAstar::estimateHeuristic(Eigen::VectorXd x1, Eigen::VectorXd x2,double& optimal_time){const Vector3d dp = x2.head(3)- x1.head(3);//位置变化量const Vector3d v0 = x1.segment(3,3);//起点速度矩阵const Vector3d v1 = x2.segment(3,3);//终点速度矩阵double c1 =-36* dp.dot(dp);double c2 =24*(v0 + v1).dot(dp);double c3 =-4*(v0.dot(v0)+ v0.dot(v1)+ v1.dot(v1));double c4 =0;double c5 = w_time_;

  std::vector&lt;double&gt; ts =quartic(c5, c4, c3, c2, c1);//求解获得极值点的Tdouble v_max = max_vel_ *0.5;double t_bar =(x1.head(3)- x2.head(3)).lpNorm<Infinity>()/ v_max;
  ts.push_back(t_bar);double cost =100000000;double t_d = t_bar;//将根带回启发函数求最优Tsfor(auto t : ts){if(t &lt; t_bar)continue;double c =-c1 /(3* t * t * t)- c2 /(2* t * t)- c3 / t + w_time_ * t;if(c &lt; cost){
      cost = c;
      t_d = t;}}

  optimal_time = t_d;return1.0*(1+ tie_breaker_)* cost;}

启发函数对T求导获得极值点或者鞍点对应的时间T，然后把多个根代回启发函数获得最优时间T。

搜索

循环搜索第一步判断当前节点是否满足停止搜索的要求

// 判断但前节点是否超出horizon或是离终点较近了bool reach_horizon =(cur_node->state.head(3)- start_pt).norm()>= horizon_;bool near_end =abs(cur_node->index(0)-end_index(0))<= tolerance &&abs(cur_node->index(1)-end_index(1))<= tolerance &&abs(cur_node->index(2)-end_index(2))<= tolerance;if(reach_horizon || near_end){
      terminate_node = cur_node;//判断其中一个达到了要求，将该节点设为终点retrievePath(terminate_node);//从终点到起点的反向路径存储到path_nodes_if(near_end){// Check whether shot traj existestimateHeuristic(cur_node->state, end_state, time_to_goal);//计算优化的最小时间computeShotTraj(cur_node->state, end_state, time_to_goal);//带入优化的时间判断轨迹是否合理if(init_search)ROS_ERROR("Shot in first search loop!");}}if(reach_horizon)if(near_end)

其中当满足终点条件时，要重新检查一下轨迹是否合理，即将轨迹带入地图，用到下面这个函数

//将计算得到的最优轨迹带入地图中检查轨迹是否安全，有没有发生碰撞，速度、加速度是否超过限制boolKinodynamicAstar::computeShotTraj(Eigen::VectorXd state1, Eigen::VectorXd state2,double time_to_goal)

当节点不满足终止条件，需要扩展节点，以当前节点为根，离散输入控制量，得到下一状态。

/* ---3）若当前节点没有抵达终点，就要进行节点扩张 ---------- *///1、在open_list中删除节点，并在close_list中添加节点
    open_set_.pop();//弹出该节点
    cur_node->node_state = IN_CLOSE_SET;//将该节点放入close节点当中
    iter_num_ +=1;//2、初始化状态传递double res =1/2.0, time_res =1/1.0, time_res_init =1/20.0;//时间常数
    Eigen::Matrix<double,6,1> cur_state = cur_node->state;//当前节点状态
    Eigen::Matrix<double,6,1> pro_state;//下一状态
    vector<PathNodePtr> tmp_expand_nodes;//临时扩展节点列表
    Eigen::Vector3d um;//控制量，本文是加速度double pro_t;//扩展节点的时间戳
    vector<Eigen::Vector3d> inputs;
    vector<double> durations;//输入控制量的持续时间//3、判断节点没有被扩展过，把这个节点存下来if(init_search){
      inputs.push_back(start_acc_);for(double tau = time_res_init * init_max_tau_; tau <= init_max_tau_ +1e-3;
           tau += time_res_init * init_max_tau_)
        durations.push_back(tau);
      init_search =false;}else{for(double ax =-max_acc_; ax <= max_acc_ +1e-3; ax += max_acc_ * res)for(double ay =-max_acc_; ay <= max_acc_ +1e-3; ay += max_acc_ * res)for(double az =-max_acc_; az <= max_acc_ +1e-3; az += max_acc_ * res){
            um << ax, ay, az;
            inputs.push_back(um);}for(double tau = time_res * max_tau_; tau <= max_tau_; tau += time_res * max_tau_)
        durations.push_back(tau);}//4、状态传递循环迭代，检查速度约束，检查碰撞，都通过的话，就计算当前节点的g_score以及f_score.并且对重复的扩展节点进行剪枝// cout << "cur state:" << cur_state.head(3).transpose() << endl;for(int i =0; i < inputs.size();++i)for(int j =0; j < durations.size();++j){
        um = inputs[i];double tau = durations[j];stateTransit(cur_state, pro_state, um, tau);//状态传递，通过前向积分得到扩展节点的位置和速度
        pro_t = cur_node->time + tau;// Check inside map range
        Eigen::Vector3d pro_pos = pro_state.head(3);if(!edt_environment_->sdf_map_->isInBox(pro_pos)){if(init_search) std::cout <<"box"<< std::endl;continue;}// Check if in close set
        Eigen::Vector3i pro_id =posToIndex(pro_pos);int pro_t_id =timeToIndex(pro_t);
        PathNodePtr pro_node =
            dynamic ? expanded_nodes_.find(pro_id, pro_t_id): expanded_nodes_.find(pro_id);if(pro_node !=NULL&& pro_node->node_state == IN_CLOSE_SET){if(init_search) std::cout <<"close"<< std::endl;continue;}// Check maximal velocity
        Eigen::Vector3d pro_v = pro_state.tail(3);if(fabs(pro_v(0))> max_vel_ ||fabs(pro_v(1))> max_vel_ ||fabs(pro_v(2))> max_vel_){if(init_search) std::cout <<"vel"<< std::endl;continue;}// Check not in the same voxel
        Eigen::Vector3i diff = pro_id - cur_node->index;int diff_time = pro_t_id - cur_node->time_idx;if(diff.norm()==0&&((!dynamic)|| diff_time ==0)){if(init_search) std::cout <<"same"<< std::endl;continue;}// Check safety
        Eigen::Vector3d pos;
        Eigen::Matrix<double,6,1> xt;bool is_occ =false;for(int k =1; k <= check_num_;++k){double dt = tau *double(k)/double(check_num_);stateTransit(cur_state, xt, um, dt);
          pos = xt.head(3);if(edt_environment_->sdf_map_->getInflateOccupancy(pos)==1||!edt_environment_->sdf_map_->isInBox(pos)){
            is_occ =true;break;}if(!optimistic_ && edt_environment_->sdf_map_->getOccupancy(pos)== SDFMap::UNKNOWN){
            is_occ =true;break;}}if(is_occ){if(init_search) std::cout <<"safe"<< std::endl;continue;}//计算代价值double time_to_goal, tmp_g_score, tmp_f_score;//计算当前节点的真实代价
        tmp_g_score =(um.squaredNorm()+ w_time_)* tau + cur_node->g_score;//计算启发函数代价
        tmp_f_score = tmp_g_score + lambda_heu_ *estimateHeuristic(pro_state, end_state, time_to_goal);/* ----------5)在循环中对比扩展节点,进行节点剪枝---------- */// Compare nodes expanded from the same parentbool prune =false;//剪枝标志位for(int j =0; j < tmp_expand_nodes.size();++j){
          PathNodePtr expand_node = tmp_expand_nodes[j];// 首先判断当前临时扩展节点与current node的其他临时扩展节点是否在同一个voxel中，如果是的话就是扩展的节点多余了，就要进行剪枝。if((pro_id - expand_node->index).norm()==0&&((!dynamic)|| pro_t_id == expand_node->time_idx)){
            prune =true;if(tmp_f_score < expand_node->f_score){
              expand_node->f_score = tmp_f_score;
              expand_node->g_score = tmp_g_score;
              expand_node->state = pro_state;
              expand_node->input = um;
              expand_node->duration = tau;if(dynamic) expand_node->time = cur_node->time + tau;}break;}}// This node end up in a voxel different from othersif(!prune){if(pro_node ==NULL){
            pro_node = path_node_pool_[use_node_num_];
            pro_node->index = pro_id;
            pro_node->state = pro_state;
            pro_node->f_score = tmp_f_score;
            pro_node->g_score = tmp_g_score;
            pro_node->input = um;
            pro_node->duration = tau;
            pro_node->parent = cur_node;
            pro_node->node_state = IN_OPEN_SET;if(dynamic){
              pro_node->time = cur_node->time + tau;
              pro_node->time_idx =timeToIndex(pro_node->time);}
            open_set_.push(pro_node);if(dynamic)
              expanded_nodes_.insert(pro_id, pro_node->time, pro_node);else
              expanded_nodes_.insert(pro_id, pro_node);

            tmp_expand_nodes.push_back(pro_node);

            use_node_num_ +=1;if(use_node_num_ == allocate_num_){
              cout <<"run out of memory."<< endl;return NO_PATH;}}// 如果不用剪枝的话，则首先判断当前临时扩展节点pro_node是否出现在open集中 elseif(pro_node->node_state == IN_OPEN_SET){if(tmp_g_score < pro_node->g_score){// pro_node->index = pro_id;
              pro_node->state = pro_state;
              pro_node->f_score = tmp_f_score;
              pro_node->g_score = tmp_g_score;
              pro_node->input = um;
              pro_node->duration = tau;
              pro_node->parent = cur_node;if(dynamic) pro_node->time = cur_node->time + tau;}}// 如果不是存在于open集的话，则可以直接将pro_node加入open集中else{
            cout <<"error type in searching: "<< pro_node->node_state << endl;}}}// init_search = false;}

  cout <<"open set empty, no path!"<< endl;
  cout <<"use node num: "<< use_node_num_ << endl;
  cout <<"iter num: "<< iter_num_ << endl;return NO_PATH;

获得规划得到的路径点

kinodynamic A*的最后一步

/*  作用：
      完成路径搜索后，按照预设的时间分辨率delta_t，通过节点回溯和状态前向积分得到分辨率最高的路径点。
    param：
      delta_t:时间分辨率
    return：
      state_list=节点扩张的回溯轨迹+两点边界轨迹
*/
std::vector<Eigen::Vector3d> KinodynamicAstar::getKinoTraj(double delta_t){
  vector<Vector3d> state_list;

  /* ---------- get traj of searching ---------- */
  PathNodePtr node= path_nodes_.back();
  Matrix<double, 6, 1> x0, xt;while(node->parent != NULL){
    Vector3d ut = node->input;
    double duration = node->duration;
    x0 = node->parent->state;for(double t = duration; t >= -1e-5; t -= delta_t){
      stateTransit(x0, xt, ut, t);
      state_list.push_back(xt.head(3));}node= node->parent;}
  reverse(state_list.begin(), state_list.end());

  /* ---------- get traj of one shot ---------- */
  if(is_shot_succ_){
    Vector3d coord;
    VectorXd poly1d, time(4);for(double t = delta_t; t <= t_shot_; t += delta_t){for(int j =0; j <4; j++)
        time(j)= pow(t, j);for(int dim =0; dim <3; dim++){
        poly1d = coef_shot_.row(dim);
        coord(dim)= poly1d.dot(time);}
      state_list.push_back(coord);}}return state_list;}

第一部分结束，未完待续。。。