文章目录
一、极大极小搜索（Minimax Algorithm）
在零和博弈（有完整信息的，确定的、轮流行动的，两个参与者收益之和为0的博弈）中，双方都希望自己获胜，因此每一步都选择对自己最有利，对对方最不利的做法。
假设我们是参与博弈的一方。我们用静态估计函数
f
(
p
)
f(p)
f(p)来估计博弈双方的态势：
- 有利于我方的态势： f ( p ) > 0 f(p)>0 f(p)>0
- 有利于敌方的态势： f ( p ) < 0 f(p)<0 f(p)<0
- 双方均衡的态势： f ( p ) = 0 f(p)=0 f(p)=0
显然，我方希望
f
(
p
)
f(p)
f(p)最大化，敌方希望
f
(
p
)
f(p)
f(p)最小化。因此称我方为Max方，敌方为Min方。
在Max方的角度，因为是我们自己做决策，我们可以选择任意一种方案，所以我们只需选择收益最大的方案，也就是说每种方案之间是“或”的关系。
而对于Min方而言，因为是敌方做决策，我们无法控制敌方选择哪种策略，假设敌方足够聪明，我们应该假设敌方选择对他最有利的方案，也就是对我们最不利的方案、使我们收益最小的方案，所以对他而言每种方案之间是“与”的关系。
假设我们在进行动态博弈——你一步，我一步，且一方做完决策之后另一方知晓他所做的决策，那么我们可以把双方的行动展开成一棵树——博弈树。
在博弈树中，每个节点代表一种格局，每条边代表Max方或Min方的一步操作。那些下一步该Max方走的节点称为Max节点，下一步该Min方走的节点称为Min节点。
博弈树的特点：
(1) 博弈的初始状态是初始节点（假如Max方为先手，则初始节点为Max节点）；
(2) Max节点是“或”节点，Min节点是“与”节点，这两种节点逐层交替出现；
(3) 整个博弈过程始终站在一方（一般为Max方）的立场上。
博弈树上有以下几种节点：
- 端节点（叶节点） - 可解节点- 非可解节点
- 与节点（Min节点）
- 或节点（Max节点）
其中，端节点可能是可解节点或非可解节点。使自己一方（Max方）获胜的为可解节点，使对方（Min）方获胜的为非可解节点。
对于当前的格局，我们的目标是找到一个最有利于自己获胜的策略。将当前棋局作为根节点，假设现在该Max方走了，Max方需要枚举根节点的所有子节点，来判断哪个子节点所对应的格局的静态估计函数的数值，那么这个节点对于Max方就最有利，Max方的下一步应该将格局转变为这个子节点的格局。
设
f
(
u
)
f(u)
f(u)是节点
u
u
u所对应的格局的静态估计函数数值（也称效用值）。
f
(
u
)
f(u)
f(u)越大，节点
u
u
u的格局对Max方越有利，对Min方越不利。显然，博弈树每层的节点类型的交替的——与节点、或节点、与节点、或节点、……，因为博弈双方是轮流采取行动的。
现在，要获得节点
u
u
u的
f
(
u
)
f(u)
f(u)值，就需要进行极小极大搜索（min-max search）。极小极大搜索是指：在有限的深度范围内，使用深度优先搜索（DFS）算法，利用递归回溯从可能的走法中选择对自己最有利的走法，即让自己的收益最大、对手的收益最小。
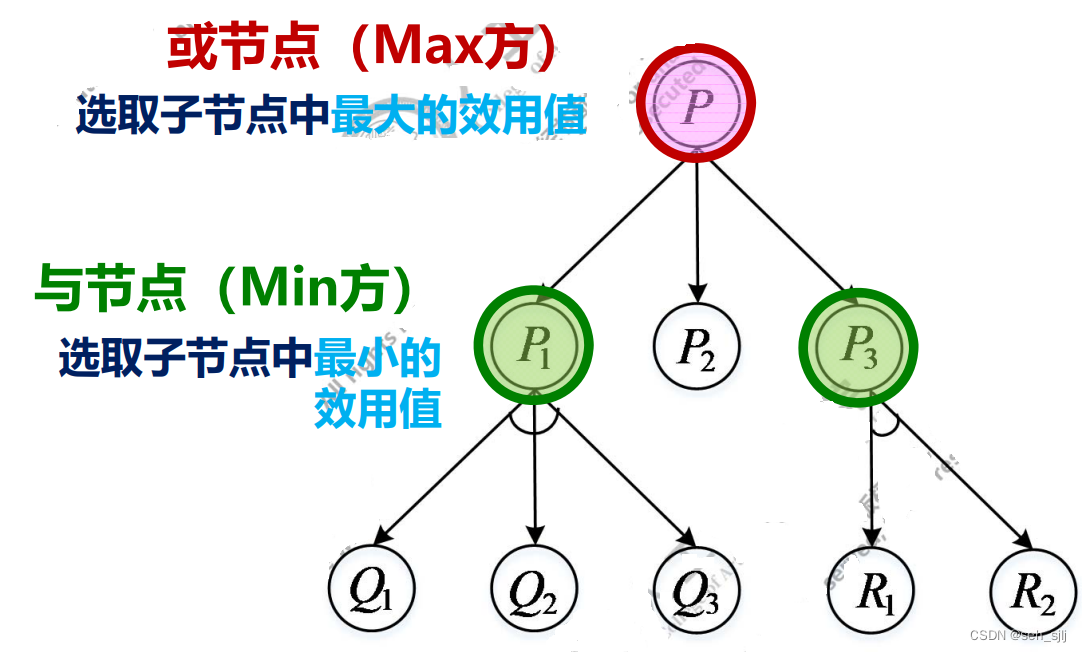
- 或节点（Max方）：该节点的效用值为所有子节点效用值的最大值。即：若节点 u u u为或节点且 u u u的子节点为 v 1 , v 2 , ⋯ , v k v_1,v_2,\cdots,v_k v1,v2,⋯,vk，则 f ( u ) = max 1 ≤ i ≤ k f ( v i ) f(u)=\max\limits_{1\le i\le k}f(v_i) f(u)=1≤i≤kmaxf(vi)。
- 与节点（Min方）：该节点的效用值为所有子节点效用值的最小值。即：若节点 u u u为与节点且 u u u的子节点为 v 1 , v 2 , ⋯ , v k v_1,v_2,\cdots,v_k v1,v2,⋯,vk，则 f ( u ) = min 1 ≤ i ≤ k f ( v i ) f(u)=\min\limits_{1\le i\le k}f(v_i) f(u)=1≤i≤kminf(vi)。
- 端节点：这类节点的效用值取决于具体问题。
由此我们可以归纳出极小极大搜索算法（Minimax Algorithm）的一般步骤：
(1) 利用广度优先搜索算法生成Max方当前状态下可猜测的
k
k
k步博弈树；
(2) 定义静态估计函数，计算端节点的效用值；
(3) 回溯评估：利用极大极小运算自下而上逐层推出各节点的效用值，其中在Max节点取最大值，在Min节点取最小值；
(4) 根据当前状态子节点的效用值做出最优决策，状态转移到子节点的状态，对方变为Max方，回到(1)开始新的搜索。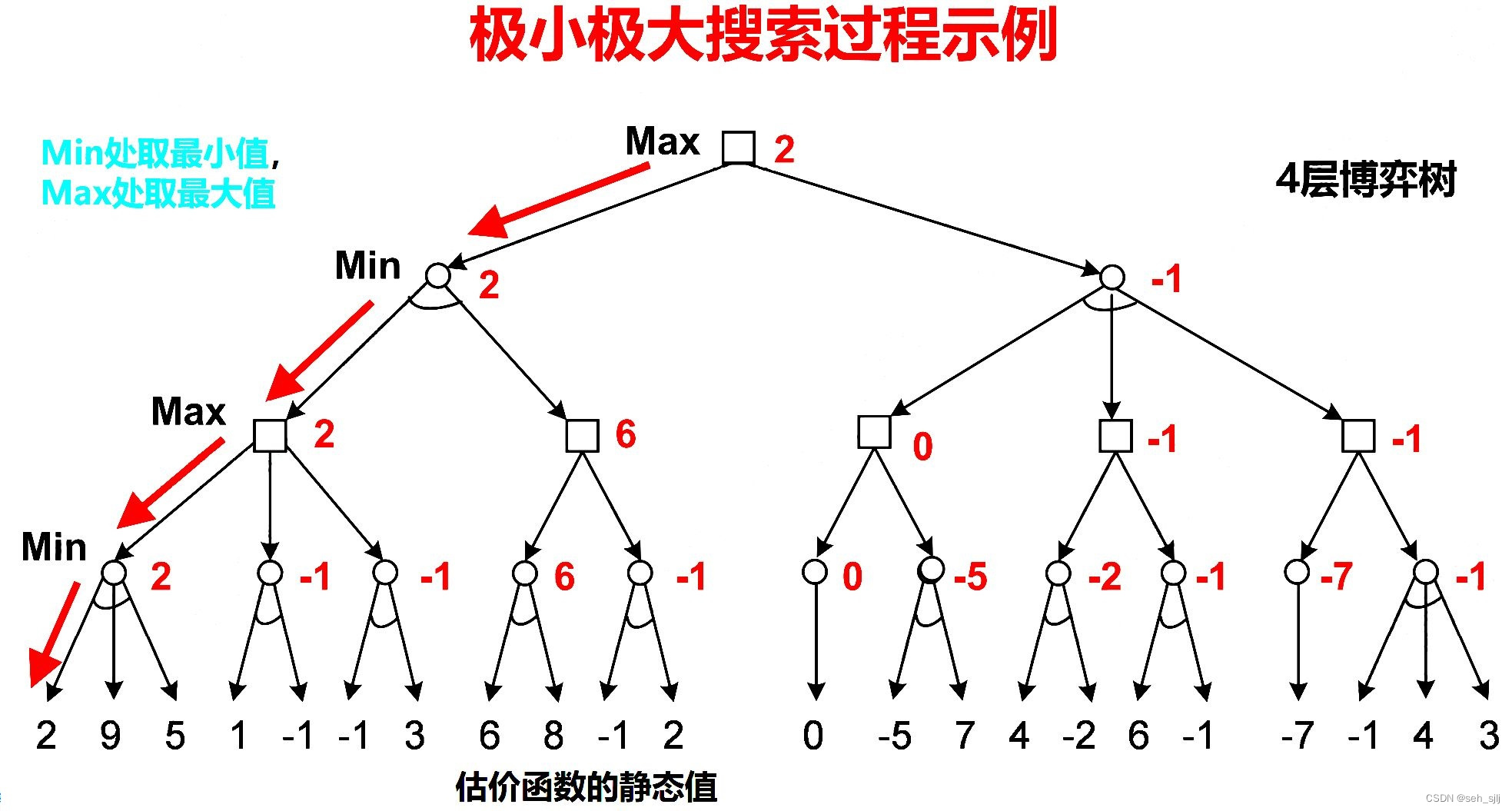
P.S. 注意画博弈数的时候，Max节点用方框表示，Min节点用圆表示，且Min节点的下方要画一条弧线！
例 （井字棋）给定一个
3
×
3
3\times3
3×3的棋盘，Max方和Min方轮流走棋，每次仅能在空格摆一个自己的棋，自己的棋子三个连成一线即为获胜。
规定估计函数
f
(
p
)
f(p)
f(p)为：
- 若格局 p p p是Max方获胜，则 f ( p ) = + ∞ f(p)=+\infty f(p)=+∞；
- 若格局 p p p是Min方获胜，则 f ( p ) = − ∞ f(p)=-\infty f(p)=−∞；
- 若双方均未获胜，则 f ( p ) = f max ( p ) − f min ( p ) f(p)=f_{\max}(p)-f_{\min}(p) f(p)=fmax(p)−fmin(p)，其中 - f max ( p ) f_{\max}(p) fmax(p)表示所有空格全放上Max方的棋子后三子一线的总数，- f min ( p ) f_{\min}(p) fmin(p)表示所有空格全放上Min方的棋子后三子一线的总数。
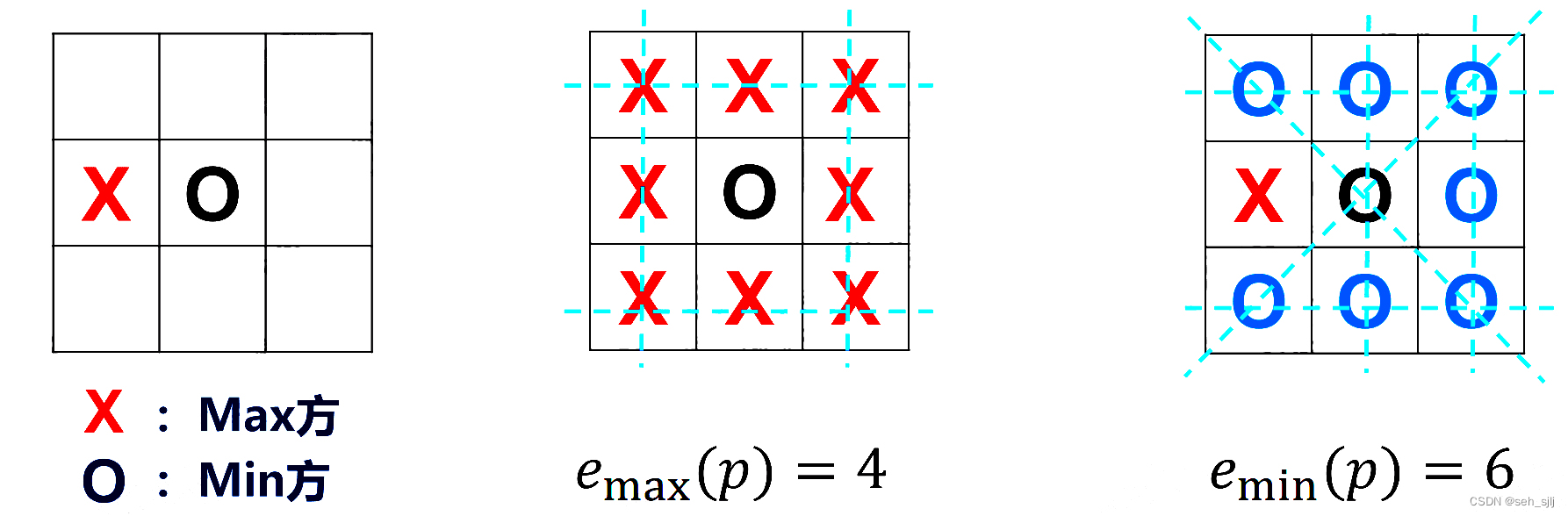那么，先手做出第一步决策的过程是这样的：
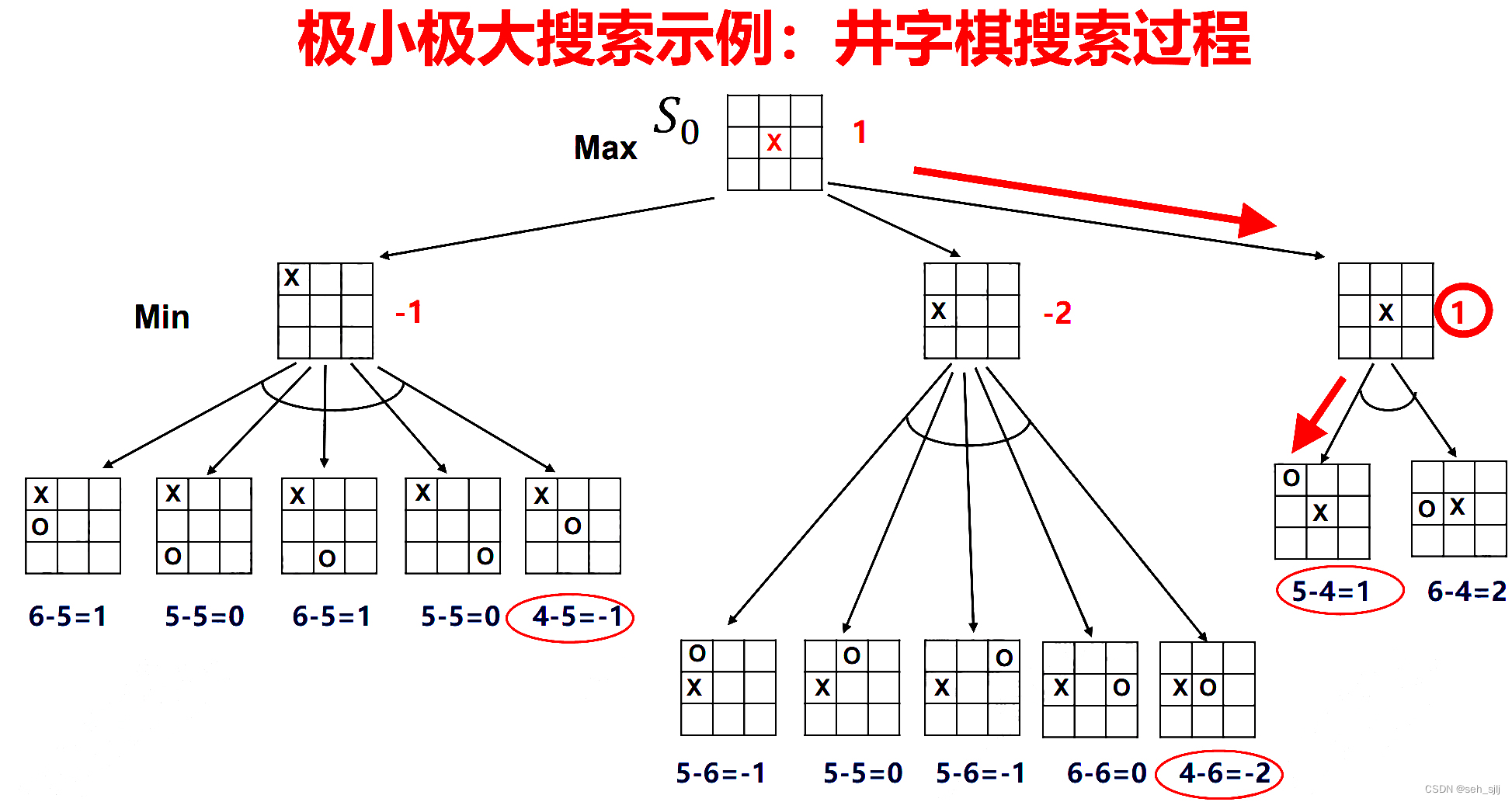
搜索过程中将很多对称的情况合并为一个情况，给出了
k
=
2
k=2
k=2步博弈树，并确定最优策略为走中间。
极大极小搜索过程比较简单，但当考虑的步数过多后就会导致博弈树太大、搜索效率变低，需要进行优化。
二、α-β剪枝（Alpha-Beta Pruning）
α-β剪枝是一种优化方法，在博弈树生成的过程中同时计算各节点的估计值及倒推值，通过对估值的上下限进行估计，减去没有用的分支，减少搜索范围，提高效率。
α-β剪枝的基本思想：
- “或”节点（Max方）：取当前子节点中效用值的极大值为该节点效用值的下界，称为α（α≥该极大值），只有当下一个节点的值大于α才会被选择
- “与”节点（Min方）：取当前子节点中效用值的极小值为该节点效用值的上界，称为β（β≤该极小值），只有当下一个节点的值小于α才会被选择
α：目前Max方可以搜索到的最好值，初始值为
−
∞
-\infty
−∞
β：目前Min方可以接受的最坏值，初始值为
+
∞
+\infty
+∞
注意：
设节点
u
u
u为或节点，
u
u
u的效用值为
f
(
u
)
f(u)
f(u)，
f
(
u
)
≥
α
f(u)\ge\alpha
f(u)≥α不一定成立。
同理，设
v
v
v为与节点，
v
v
v的效用值为
f
(
v
)
f(v)
f(v)，
f
(
v
)
≤
β
f(v)\le\beta
f(v)≤β也不一定成立。
α，β是中间量，它们的作用是排除对结果没有影响的分支，不能决定最终节点的效用值。
或节点（Max方）α剪枝规则：
设当前节点为
u
u
u，
u
u
u是或节点，则
u
u
u的子节点都是与节点或端节点，设为
v
1
,
v
2
,
⋯
,
v
k
v_1,v_2,\cdots,v_k
v1,v2,⋯,vk。我们在扫描
v
1
,
v
2
,
⋯
,
v
k
v_1,v_2,\cdots,v_k
v1,v2,⋯,vk的过程中，若发现
v
i
v_i
vi的β值小于等于其**任何祖先节点**的α值时，则对该节点以下的分支停止搜索，且
v
i
v_i
vi的最终倒推值就是其β值（可能与未加优化的极大极小搜索的结果不同）。
与节点（Min方）β剪枝规则：
设当前节点为
v
v
v，
v
v
v是与节点，则
v
v
v的子节点都是或节点或端节点，设为
u
1
,
u
2
,
⋯
,
u
k
u_1,u_2,\cdots,u_k
u1,u2,⋯,uk。我们在扫描
u
1
,
u
2
,
⋯
,
u
k
u_1,u_2,\cdots,u_k
u1,u2,⋯,uk的过程中，若发现
u
i
u_i
ui的α值大于等于其**任何祖先节点**的β值时，则对该节点以下的分支停止搜索，且
u
i
u_i
ui的最终倒推值就是其α值（可能与未加优化的极大极小搜索的结果不同）。
用一个实际的例子来说明：如果你和一个人在下棋，现在轮到你走。现在你有两种选择：走“A”或者走“B”。如果走“A”，那么你的局势会变好。走“B”也比较好，但是如果你走“B”的话，对方可以在两步之内获胜，这对你是非常不利的。也就是说，你考虑到了走“B”的最坏结果，那么其他可能的结果就可以不考虑了（因为对手不傻，肯定会想方设法使你败北），那么你相当于在博弈树中剪掉了“B”的其他情况。最终，因为“A”至少不会让你在两步以内输棋，所以你选择走“A”。（摘自维基百科）
核心思想是：如果存在一个比某一分支更好的走法，那么就不考察这一分支。
α-β剪枝的一个Python实现：
# encoding: GB2312
tree =[# 博弈树的结构[[[4,8,6],[1,9]],[[5,8],[-1,2]]],[[[0,3],[-6,6]],[[1],[0,9,-7]]]]defis_terminal(node):# 判断是否为端节点returnisinstance(node,int)
infinity =int(1e10)# 无穷大defalpha_beta(node, alpha, beta, ismax):# node: 当前节点# ismax: 若为True则当前节点是Max节点，否则为Min节点# 当node为Max节点时，alpha为当前节点的α，beta为父节点的β# 当node为Min节点时，alpha为父节点的α，beta为当前节点的βif is_terminal(node):return node # 若当前节点为端节点，直接返回其效用值if ismax:
value =-infinity # 当前节点的效用值for child in node:
value =max(value,
alpha_beta(child, alpha, beta,False))# 当前节点的效用值是子节点效用值的最大值
alpha =max(alpha, value)if value >= beta:# 这个子节点的效用值不小于beta，不可能被选择break# 进行β剪枝return value
else:
value =+infinity
for child in node:
value =min(value,
alpha_beta(child, alpha, beta,True))
beta =min(beta, value)if value <= alpha:# 这个子节点的效用值不大于alpha，不可能被选择break# alpha剪枝return value
print(alpha_beta(tree,-infinity,+infinity,True))
三、解题技巧
对于我们的期末考试而言，给你一棵树，请问需要在哪里剪枝。其实我们并不需要搞那些α，β什么的，只需要简单的逻辑就能算出来。
考虑下面的树：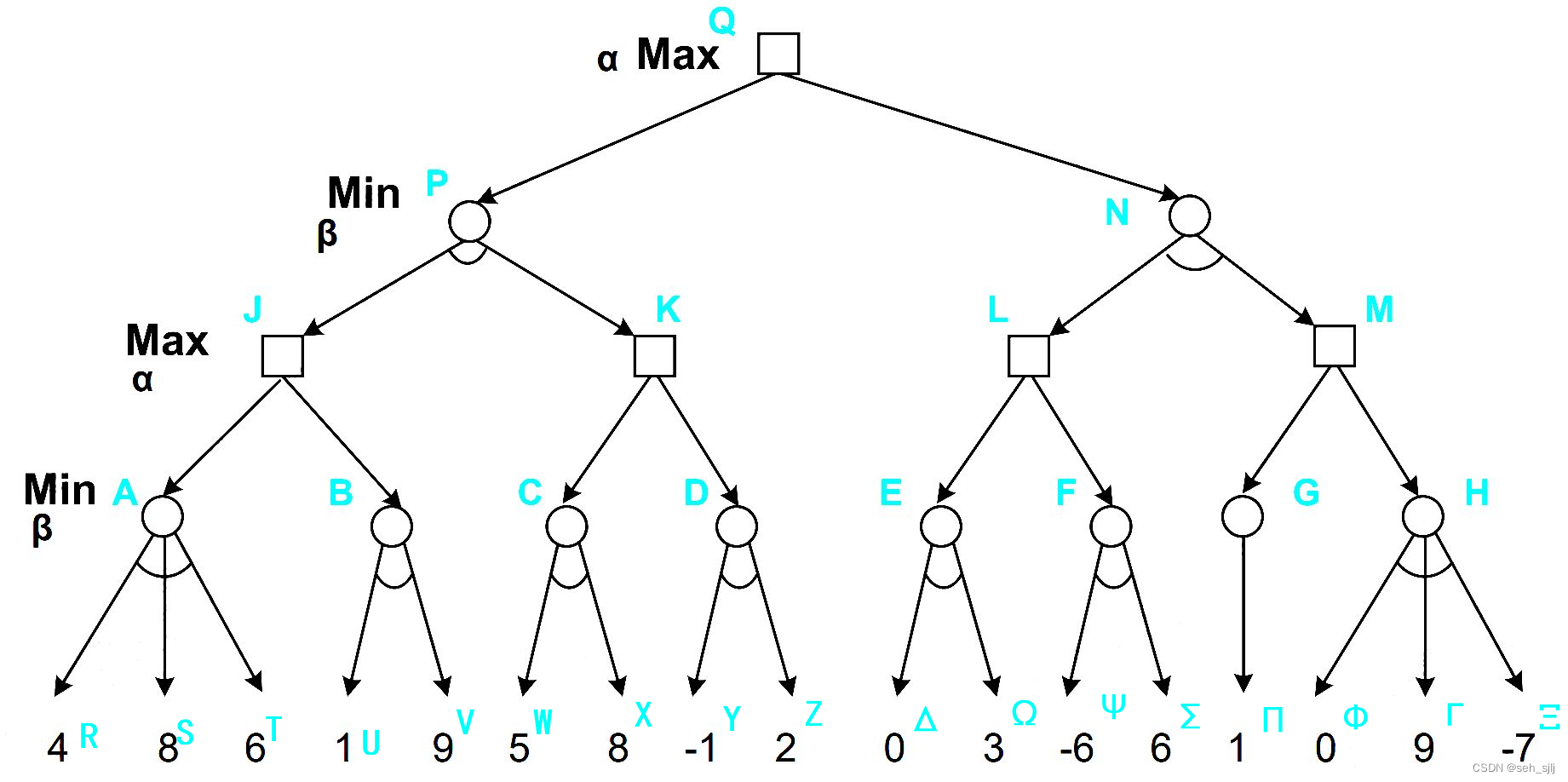
首先我们假设路线是
Q
→
P
→
J
→
A
→
R
Q\to P\to J\to A\to R
Q→P→J→A→R。现在考虑节点
A
A
A。Min方不选择去
R
R
R而是选择去其他端节点的条件是什么呢？是其他端节点的效用值小于
f
(
R
)
=
4
f(R)=4
f(R)=4。但是
f
(
S
)
=
8
f(S)=8
f(S)=8和
f
(
T
)
=
6
f(T)=6
f(T)=6都大于
4
4
4，所以Min方还是选择去
R
R
R。所以
f
(
A
)
=
min
{
4
,
8
,
6
}
=
4
f(A)=\min\{4,8,6\}=4
f(A)=min{4,8,6}=4。
现在考虑节点
J
J
J。Max方选择去
B
B
B而不是去
A
A
A的条件是什么呢？就是
f
(
B
)
>
f
(
A
)
=
4
f(B)>f(A)=4
f(B)>f(A)=4。而
f
(
B
)
=
min
{
f
(
U
)
,
f
(
V
)
}
f(B)=\min\{f(U),f(V)\}
f(B)=min{f(U),f(V)}，所以转化为
min
{
f
(
U
)
,
f
(
V
)
}
>
4
\min\{f(U),f(V)\}>4
min{f(U),f(V)}>4，即
[
f
(
U
)
>
4
]
∧
[
f
(
V
)
>
4
]
[f(U)>4]\land[f(V)>4]
[f(U)>4]∧[f(V)>4]这是一个且的关系。现在
f
(
U
)
=
1
f(U)=1
f(U)=1，
f
(
U
)
>
4
f(U)>4
f(U)>4已经不满足了，所以这个且的关系肯定不成立，不论
f
(
V
)
f(V)
f(V)是多少都不可能成立，所以Max方不会去
B
B
B。因此要把
V
V
V剪掉，
f
(
J
)
=
f
(
A
)
=
4
f(J)=f(A)=4
f(J)=f(A)=4。
再考虑节点
P
P
P。Min方去
K
K
K而不是去
J
J
J的条件是什么呢？就是
f
(
K
)
<
f
(
J
)
=
4
f(K)<f(J)=4
f(K)<f(J)=4。而
f
(
K
)
=
max
{
f
(
C
)
,
f
(
D
)
}
f(K)=\max\{f(C),f(D)\}
f(K)=max{f(C),f(D)}，故转化为
[
f
(
C
)
<
4
]
∧
[
f
(
D
)
<
4
]
[f(C)<4]\land[f(D)<4]
[f(C)<4]∧[f(D)<4]又
f
(
C
)
=
min
{
f
(
W
)
,
f
(
X
)
}
f(C)=\min\{f(W),f(X)\}
f(C)=min{f(W),f(X)}，
f
(
D
)
=
min
{
f
(
Y
)
,
f
(
Z
)
}
f(D)=\min\{f(Y),f(Z)\}
f(D)=min{f(Y),f(Z)}，又转化为
{
[
f
(
W
)
<
4
]
∨
[
f
(
X
)
<
4
]
}
∧
{
[
f
(
Y
)
<
4
]
∨
[
f
(
Z
)
<
4
]
}
\{[f(W)<4]\lor[f(X)<4]\}\land\{[f(Y)<4]\lor[f(Z)<4]\}
{[f(W)<4]∨[f(X)<4]}∧{[f(Y)<4]∨[f(Z)<4]}其中
f
(
W
)
=
5
f(W)=5
f(W)=5、
f
(
X
)
=
8
f(X)=8
f(X)=8，都不小于
4
4
4，所以
[
f
(
W
)
<
4
]
∨
[
f
(
X
)
<
4
]
[f(W)<4]\lor[f(X)<4]
[f(W)<4]∨[f(X)<4]不成立，那么
f
(
K
)
<
4
f(K)<4
f(K)<4也不可能成立，所以就没必要考察
D
D
D了，把
D
D
D剪掉，并令
f
(
P
)
=
4
f(P)=4
f(P)=4。
再考虑节点
Q
Q
Q。Max方不去
P
P
P而是去
N
N
N的节点是什么呢？是
f
(
N
)
>
f
(
P
)
=
4
f(N)>f(P)=4
f(N)>f(P)=4。而
f
(
N
)
=
min
{
f
(
L
)
,
f
(
M
)
}
f(N)=\min\{f(L),f(M)\}
f(N)=min{f(L),f(M)}，故转化为
[
f
(
L
)
>
4
]
∧
[
f
(
M
)
>
4
]
[f(L)>4]\land[f(M)>4]
[f(L)>4]∧[f(M)>4]而
f
(
L
)
=
max
{
f
(
E
)
,
f
(
F
)
}
f(L)=\max\{f(E),f(F)\}
f(L)=max{f(E),f(F)}，
f
(
M
)
=
max
{
f
(
G
)
,
f
(
H
)
}
f(M)=\max\{f(G),f(H)\}
f(M)=max{f(G),f(H)}，故转化为
{
[
f
(
E
)
>
4
]
∨
[
f
(
F
)
>
4
]
}
∧
{
[
f
(
G
)
>
4
]
∨
[
f
(
H
)
>
4
]
}
\{[f(E)>4]\lor[f(F)>4]\}\land\{[f(G)>4]\lor[f(H)>4]\}
{[f(E)>4]∨[f(F)>4]}∧{[f(G)>4]∨[f(H)>4]}又
f
(
E
)
=
min
{
f
(
Δ
)
,
f
(
Ω
)
}
f(E)=\min\{f(\Delta),f(\Omega)\}
f(E)=min{f(Δ),f(Ω)}，
f
(
F
)
=
min
{
f
(
Ψ
)
,
f
(
Σ
)
}
f(F)=\min\{f(\Psi),f(\Sigma)\}
f(F)=min{f(Ψ),f(Σ)}，
f
(
G
)
=
f
(
Π
)
f(G)=f(\Pi)
f(G)=f(Π)，
f
(
H
)
=
min
{
f
(
Φ
)
,
f
(
Γ
)
,
f
(
Ξ
)
}
f(H)=\min\{f(\Phi),f(\Gamma),f(\Xi)\}
f(H)=min{f(Φ),f(Γ),f(Ξ)}，故转化为
{
[
f
(
Δ
)
>
4
∧
f
(
Ω
)
>
4
]
∨
[
f
(
Ψ
)
>
4
∧
f
(
Σ
)
>
4
]
}
∧
{
[
f
(
Π
)
>
4
∨
f
(
Φ
)
>
4
]
∧
[
f
(
Γ
)
>
4
∨
f
(
Ξ
)
>
4
]
}
\{[f(\Delta)>4\land f(\Omega)>4]\lor[f(\Psi)>4\land f(\Sigma)>4]\}\land\{[f(\Pi)>4\lor f(\Phi)>4]\land[f(\Gamma)>4\lor f(\Xi)>4]\}
{[f(Δ)>4∧f(Ω)>4]∨[f(Ψ)>4∧f(Σ)>4]}∧{[f(Π)>4∨f(Φ)>4]∧[f(Γ)>4∨f(Ξ)>4]}观察这个式子。这个式子成立，需要
{
[
f
(
Δ
)
>
4
∧
f
(
Ω
)
>
4
]
∨
[
f
(
Ψ
)
>
4
∧
f
(
Σ
)
>
4
]
}
\{[f(\Delta)>4\land f(\Omega)>4]\lor[f(\Psi)>4\land f(\Sigma)>4]\}
{[f(Δ)>4∧f(Ω)>4]∨[f(Ψ)>4∧f(Σ)>4]}和
{
[
f
(
Π
)
>
4
]
∨
[
f
(
Φ
)
>
4
∧
f
(
Γ
)
>
4
∧
f
(
Ξ
)
>
4
]
}
\{[f(\Pi)>4]\lor[f(\Phi)>4\land f(\Gamma)>4\land f(\Xi)>4]\}
{[f(Π)>4]∨[f(Φ)>4∧f(Γ)>4∧f(Ξ)>4]}都成立。而前者成立，只需使
[
f
(
Δ
)
>
4
∧
f
(
Ω
)
>
4
]
[f(\Delta)>4\land f(\Omega)>4]
[f(Δ)>4∧f(Ω)>4]或
[
f
(
Ψ
)
>
4
∧
f
(
Σ
)
>
4
]
[f(\Psi)>4\land f(\Sigma)>4]
[f(Ψ)>4∧f(Σ)>4]成立。
现在
f
(
Δ
)
=
0
f(\Delta)=0
f(Δ)=0不大于
4
4
4，故
[
f
(
Δ
)
>
4
∧
f
(
Ω
)
>
4
]
[f(\Delta)>4\land f(\Omega)>4]
[f(Δ)>4∧f(Ω)>4]不成立，不论
f
(
Ω
)
f(\Omega)
f(Ω)为何值，因此剪掉
Ω
\Omega
Ω。而
f
(
Ψ
)
=
−
6
f(\Psi)=-6
f(Ψ)=−6也不大与4，故
[
f
(
Ψ
)
>
4
∧
f
(
Σ
)
>
4
]
[f(\Psi)>4\land f(\Sigma)>4]
[f(Ψ)>4∧f(Σ)>4]不成立，不论
f
(
Σ
)
f(\Sigma)
f(Σ)为和值，因此剪掉
Σ
\Sigma
Σ。这意味着，
{
[
f
(
Δ
)
>
4
∧
f
(
Ω
)
>
4
]
∨
[
f
(
Ψ
)
>
4
∧
f
(
Σ
)
>
4
]
}
\{[f(\Delta)>4\land f(\Omega)>4]\lor[f(\Psi)>4\land f(\Sigma)>4]\}
{[f(Δ)>4∧f(Ω)>4]∨[f(Ψ)>4∧f(Σ)>4]}不成立。那么
f
(
N
)
>
f
(
P
)
f(N)>f(P)
f(N)>f(P)的条件就已经不能满足了，
N
N
N这边彻底没戏了，所以把剩下没去过的的都剪掉——也就是把
M
M
M剪掉。最后，
f
(
Q
)
=
f
(
P
)
=
4
f(Q)=f(P)=4
f(Q)=f(P)=4，也就是说在
Q
Q
Q状态下Max方选择去
P
P
P。
综上，要剪掉的节点是
V
,
D
,
Ω
,
Σ
,
M
V,D,\Omega,\Sigma,M
V,D,Ω,Σ,M。如下图所示：
本文转载自: https://blog.csdn.net/qaqwqaqwq/article/details/127476404
版权归原作者 seh_sjlj 所有， 如有侵权，请联系我们删除。
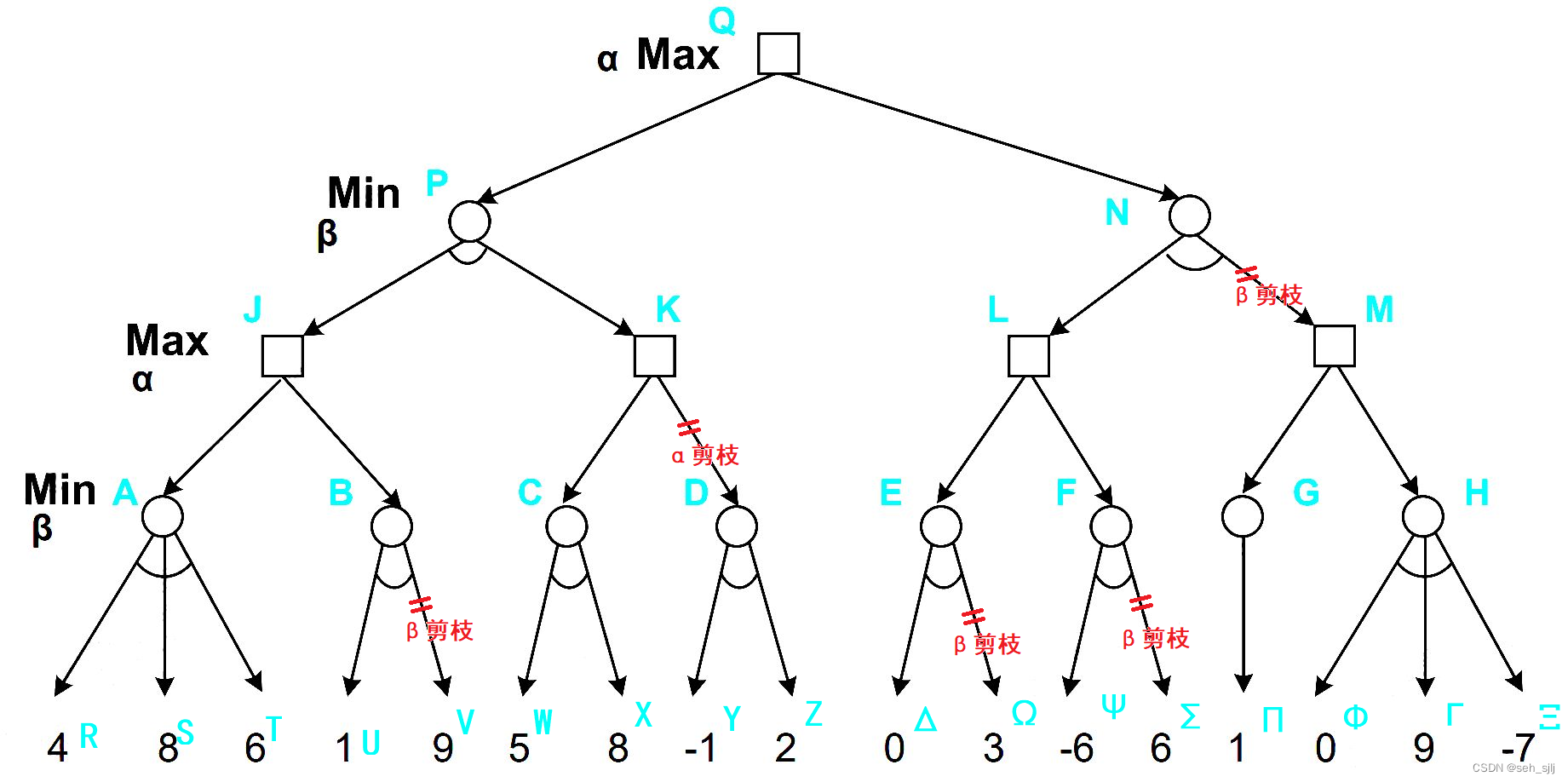
版权归原作者 seh_sjlj 所有， 如有侵权，请联系我们删除。