在大部份情况下我们都可以使用 PCA 进行线性降维。从图像处理到非结构化数据,无时无刻不在。我们甚至可以将它用于时间序列分析,虽然有更好的技术。在这篇文章中,我想向您介绍动态模式分解 (DMD),这是一种源自我的研究领域:流体动力学的用于高维时间序列的线性降维技术。DMD 结合了两个世界中的优点:PCA 和傅立叶变换。在数学上,它与动力系统理论中的一个基本算子有关,称为 Koopman 算子。但在深入研究 DMD 的数学之前,让我们用一个相当简单的例子来说明为什么 PCA 不是高维时间序列分析的最佳选择。

这个动画, 它由 1024 帧 128 x 128 像素的图像组成。从概念上讲,这是一个高维时间序列。尽管有 16 384 个自由度,但很明显存在潜在的低阶结构。毕竟,这部动画只是由以两种不同频率振荡的正方形和圆形加上一些随机噪声组成。通过将每一帧重铸为一个 16 384 维的向量,我们可以构建数据矩阵 X,其中每一列都是不同的帧。因此,它是一个 16 384 x 1024 的矩阵。现在让我们使用 PCA 来解开这个低秩结构。PCA 依赖于 X 的奇异值分解,即:

其中 U 包含 PCA 模式,Σ 的对角线条目描述了这些模式中的每一个的重要性,而 V 的列描述了它们的时间演变。此外,UᵀU = I,即 PCA 模式形成正交基。类似地,VᵀV = I 意味着它们的时间演化是线性不相关的。下图描绘了奇异值分布以及两种主要的 PCA 模式。
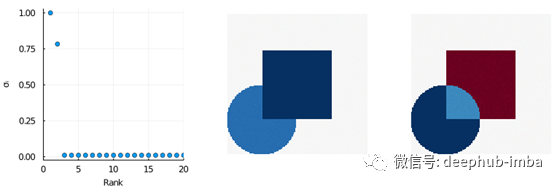
PCA 分析的结果。左:奇异值分布。中右:两种主要 PCA 模式的空间支持。
正如预期的那样,我们数据集中的大部分差异都是由前两种模式捕获的。然而,它们对应于正方形和圆形的混合。在查看下面的时间演变时,这种无法将两者分开的情况尤为明显。
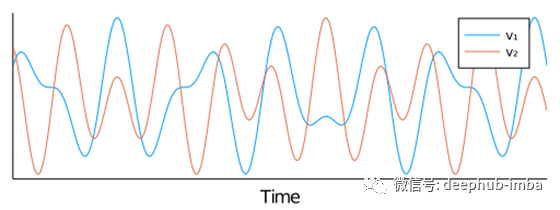
两种主要PCA模式的时间演化。
虽然PCA识别了一个良好的低维子空间,但相关的坐标系并不能提供对正在进行的简单动力学的清晰理解。我们能做得更好吗?我们能否同时找到一个好的低维嵌入和坐标系来描述这些动态?
动态模式分解 Dynamic Mode Decomposition
从数学上讲,主成分分析主要用于描述数据集的二阶统计数据,而不是动态数据。DMD来了。假设我们的数据是由一个未知的动态过程产生的

我们的目标是找到一个函数 h(x): ℝⁿ ↦ ℝⁿ 在最小二乘意义上逼近 f(x): ℝⁿ ↦ ℝⁿ 。关于 h(x) 的不同假设导致不同的模型。在DMD框架中,假设h(x)是一个线性映射

其中A是一个n × n矩阵。现在的问题是如何确定矩阵A?
数学细节
在没有附加信息的情况下,我们能得到的最佳解决方案是通过求解优化问题
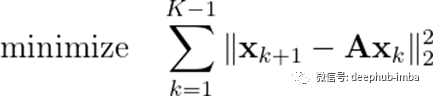
引入矩阵X和Y的定义为
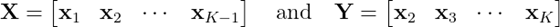
这个优化问题可以改写为

它的解是
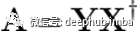
其中X†表示X的Moore-Penrose伪逆。尽管容易计算,这个解受到两个限制,这两个限制都与A是一个n × n矩阵有关。由于n在高维条件下通常是几百万,显式地构造这个矩阵可能是不可能的。这也意味着我们有n²个参数,远远超过我们有限的数据集允许我们合理估计的。因此,即使我们能构造出a,这个模型也很难推广。
为了克服这些限制,我们可以假设A是低秩的。如果是,它可以因式分解为

其中 P 和 Q 是 n × r 矩阵。在不失一般性的情况下,我们还强加 PᵀP = I,其中 I 为 r × r 单位矩阵。将这种分解引入我们的优化问题会产生
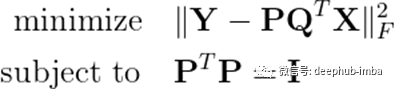
这是一个非凸问题。然而,使用简单的代数运算,可以得到 P 和 Q 作为
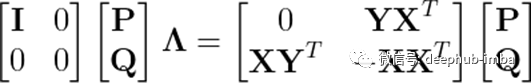
到目前为止,我们还没有指定我们的线性模型的等级。然而,这是一个广义的 Hermitian 特征问题。所有的特征值都是非负的。因此,可以使用与 PCA 相同的启发式方法来确定我们模型的最佳等级。PCA 实际上是这个更普遍问题的一个特例。事实上,假设 X = Y 和 P = Q,它简化为 PCA 特征问题。
与 PCA 相比,DMD 的亮点在于它不仅提供了低维嵌入,而且还适合我们未知动态过程的线性模型

计算出低秩分解 A = PQᵀ 后,它可以很容易地转化为它的特征分解

其中 Ψ 和 ϕ 分别是 A 的左特征向量和右特征向量。它们也称为 DMD 模式。D 是由 A 的特征值组成的对角矩阵。我们的线性模型现在可以重写为
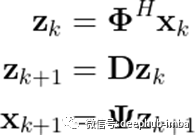
因此,Ψ 和 ϕ 是投影进出低维空间的矩阵。此外,在这个潜在空间中,动力学近似于一个简单的对角矩阵。正如我们将看到的,这使得我们的嵌入比我们使用 PCA 的嵌入更具可解释性。
示例
让我们回到我们的激励示例并使用 DMD 处理数据。下图描述了广义 Hermitian 特征问题的特征值和 DMD 模式的空间支持。

DMD 分析的结果。左:广义 Hermitian 特征问题的特征值。中和右:两种主要 DMD 模式的空间支持(Ψ 矩阵的第一列和第二列)。
至于 PCA,特征值分布表明是 2 级模型,而 DMD 模式现在清楚地将这两种动态分开。在绘制每个潜在变量的时间演变时,这也是可见的。
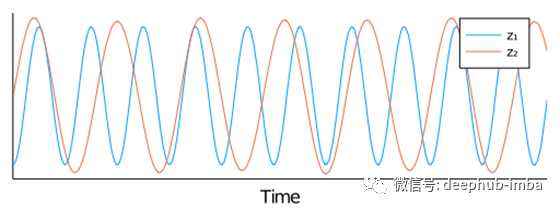
两种主要 DMD 模式的时间演变。
正如预期的那样,DMD 恢复了两个纯音振荡。最近的研究表明,DMD 表现为一种源分离算法(例如 ICA),尽管该框架可以更加灵活。对于类似的计算成本,它还提供了比 PCA 更具可解释性的模型!
热对流在流体动力学中的应用
在结束之前,让我展示一个实际示例,其灵感来自我自己的研究 [1],其中 DMD 发挥了重要作用。左侧显示的配置是热虹吸管。它是一个闭环,流体从下方加热并从上方冷却。随着上下壁之间的温差增加,热流体开始上升,冷流体开始下降。这种运动产生了对流单元。超过临界温差,动力学变得混乱。对流单元经历随机逆转,导致它以顺时针或逆时针方向来回振荡。在某种程度上,这是一些地球物理流的简化版本。
我研究的一个关键目标是确定此类流动的低阶模型,我们可以将其用于快速预测或反馈控制。然而,先决条件是对数据进行良好的低维嵌入。这就是 DMD 出现的地方。在收集了相当多的温度和速度场快照后,进行了 DMD 分析。结果如下所示。
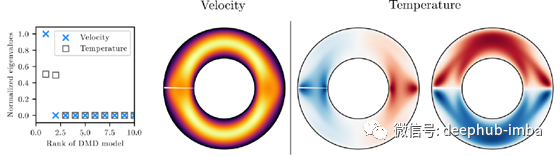
混沌热虹吸管的 DMD 分析。1 级模型捕获速度场中的大部分动态,而 2 级模型需要用于温度。
尽管问题中有大量的自由度,但动力学的内在维度是 3。一个是速度,两个是温度。DMD 模式强调速度场中的主导模式在方位角方向上基本上是不变的。对于温度,它表明最重要的模式是左右和上下温差。这几乎是您对动力学建模所需的全部内容(但这是另一个故事)。将数据投影到这些 DMD 模式的跨度上会产生以下低维嵌入。
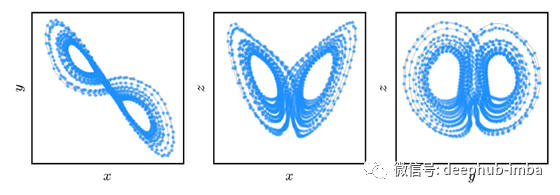
从 DMD 分析获得的低维嵌入。x 变量表示与速度场相关的模式的幅度,而 y 和 z 是左右和上下反对称温度分布的幅度。
对于稍微熟悉混沌理论的人来说,这种低维潜在空间动力学看起来就像洛伦兹系统!这确实是出于我没有时间在这篇文章中解释的原因。您应该记住的基本上是,即使对于这种强非线性、高维、混沌动力系统,DMD 也提供了有关该系统物理特性的大量见解。
总结
由于其简单性,PCA 在数据科学中无处不在。由于这种简单性,事实证明它也经常用于不应该使用或存在同样简单但更好的方法的情况。高维时间序列分析就是这样的一个例子。我希望您现在确信,在这种情况下,动态模式分解会更好。它不仅旨在处理顺序数据,而且还提供了比 PCA 在几乎相同的计算成本下所能提供的更具可解释性的模型。
自从十年前引入流体动力学 [2, 3] 以来,DMD 已被证明是一种极其通用且强大的框架,可用于分析由高维动力学过程生成的数据。它现在经常用于其他领域,如视频处理或神经科学。还提出了许多扩展。有些包括用于控制目的的输入和输出[4]。其他人将 DMD 与来自压缩感知的想法相结合,以进一步降低计算成本和数据存储 [5],或将小波用于多分辨率分析 [6]。可能性是无止境。如果您想了解更多信息,我强烈建议您阅读 Kutz 及其同事所著的《动态模式分解:复杂系统的数据驱动建模》一书 [7]。您还可以查看文章末尾的参考资料。如果您觉得 DMD 实际上是您缺少的工具,请告诉我!
引用
[1] Loiseau J.-Ch. Data-driven modeling of the chaotic thermal convection in an annular thermosyphon. Theoretical and Computational Fluid Dynamics, 34(4), pp. 339–365. 2020.
[2] Schmid P. J. Dynamic mode decomposition of numerical and experimental data. Journal of Fluid Mechanics, 656, pp. 5–28. 2010
[3] Rowley C. W., Mezic I., Bagheri S., Schlatter P., and Henningson D. Spectral analysis of nonlinear flows. Journal of Fluid Mechanics, 641, pp. 115–127. 2009
[4] Proctor J. L., Brunton S. L., and Kutz J. N. Dynamic mode decomposition with control. SIAM Journal on Applied Dynamical Systems, 15(1), pp. 142–161. 2016.
[5] Brunton S. L., Proctor J. L., Tu J. H., and Kutz J. N. Compressed sensing and dynamic mode decomposition. Journal of Computational Dynamics, 2(2). 2015
[6] Kutz J. N., Fu X., and Brunton S. L. Multiresolution dynamic mode decomposition. SIAM Journal on Applied Dynamical Systems, 15(2), pp. 713–735. 2016.
[7] Kutz J. N., Brunton S. L., Brunton B. W., and Proctor J. L. Dynamic mode decomposition: data-driven modeling of complex systems. SIAM, 2016.
作者:Jean-Christophe B. Loiseau
原文地址:https://towardsdatascience.com/a-case-against-pca-for-time-series-analysis-ac66b47629e0