点击上方“Deephub Imba”,关注公众号,好文章不错过 !
前言
一般情况下我们都是使用折线图绘制和监控我们的损失函数, y 轴是损失函数的值,x 轴是训练的轮次。这种情况下我们只有损失函数空间的一维视图,并且只能看到小范围的参数梯度。
有没有一种方法能够让我们将的GPT的1750亿参数损失空间进行可视化呢?如果可以的话,那么这数十亿个参数的梯度会怎样?虽然理论上是可行的,但是这么大的参数对于我们现在的硬件条件来说还是不可行的,但是如果我们至少可以在一个小维度(比如,3维)空间中看到损失图像,这样是否可行呢?这篇介绍性文章简要说明了它是如何实现的,以及它是一个多么简单而又引人入胜的想法。
You can’t step past [someone] in this [two] dimension. Observe this two-dimensional egg. If we were in the third dimension, looking down, we’d be able to see an unhatched chick in it, just as a chick inside a three-dimensional egg could be seen by an observer in the fourth dimension
Prof. Farnsworth, Futurama E15S7

在训练神经网络时,我们绘制的损失函数会根据模型架构、优化器、初始化方法等不同配置而不同。虽然这些选择对最终目标的影响尚不清楚,但是我们可以将损失函数的收敛进行可视化,这不仅是为了好玩,也是为了深入了解训练的过程以及结果。损失函数三维图的有助于解释为什么神经网络可以优化极其复杂的非凸函数,以及为什么优化的最小值能够很好地被推广。(例如,通过这种可视化观察到了对残差连接的一个有用的现象:它们可以防止模型将损失三维图变得混乱,因此在训练中很有用 [3])。
数据集
为简单起见本文使用 MNIST 数据集,并探讨了可视化的几个方面。更多关于其他数据集和这个想法方面的学术研究可以在关于这个问题的论文中找到 [2, 3, 4],首先让我们配置dataset和dataloader
from torchvision import transforms as T
transform = T.Compose([
T.ToTensor(),
T.Resize((28,28)),
T.Normalize((0.1307,), (0.3081,))
])
dataset = Dataset(root='data', download=True, train=False, transform=transform)
dataloader = torch.utils.data.DataLoader(dataset,
batch_size=len(dataset),
pin_memory=True, num_workers=4)
目标
然后,我们设 𝛉 是一个神经网络中所有参数的列表。令𝓛(𝑦, 𝑡; 𝛉) 作为损失函数,其中𝑦 是预测,𝑡 是目标。我们通常绘制 𝓛 的收敛性以可视化 𝑦 和 𝑡 之间的差异。但是在这里我们的目标略有不同。我们要让这个损失函数的输入 𝑦 和 𝑡 保持不变。换句话说,我们打算绘制的图是 关于𝛉 的函数,即𝓛(𝛉; 𝑦, 𝑡),或者简称为𝓛(𝛉)。我们要绘制的是对于一个给定的域,我们对网络架构、优化器、损失函数等的配置在图形上表现是什么样的。
import torch
from torch.nn import functional as F
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = torch.nn.Conv2d(1, 32, (3,3))
self.conv2 = torch.nn.Conv2d(32, 64, (3,3))
self.drop1 = torch.nn.Dropout2d(0.25)
self.drop2 = torch.nn.Dropout2d(0.5)
self.fc1 = torch.nn.Linear(9216, 128)
self.fc2 = torch.nn.Linear(128, 10)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.relu(self.conv2(x))
x = self.drop1(F.max_pool2d(x, 2))
x = x.flatten(1)
x = F.relu(self.fc1(x))
x = self.drop2(x)
x = self.fc2(x)
return F.log_softmax(x, 1)
具有两个卷积层的简单 NN 足以对 MNIST 数据集进行分类和进行演示
这里的𝛉 肯定是高维的(上面代码片段中的简单网络有 1,199,882 维!)。但是现实将我们限制在只有三维中——至少就可视化而言。所以,我们需要减少这个维度。一种简单的方法是从欧几里得空间移动到较低维度(一维或二维)的超空间。简单来说,在欧几里得空间中具有 d 维的 𝛉 可以被认为是超空间的一维表示。𝓛(𝛉; 𝑦, 𝑡) 的图是一个二维图。同样,如果我们假设 𝛉 在超空间中是二维的,我们就有了一个理想的三维图。
使用低阶维度可视化
一维
将损失绘制为一维图 [1] 很简单:它首先测量从一组参数 𝛉 到另一组参数 𝛉* 的损失,其中 𝛉 可能是一个随机初始化的集合,指向(已经找到的)局部(甚至全局)最优,𝛉*。
from torch.nn.utils import (
parameters_to_vector as Params2Vec,
vector_to_parameters as Vec2Params
)
learnt_model = 'models/learnt.pt'
learnt_net = Net()
learnt_net.load_state_dict(torch.load(learnt_model))
theta_ast = Params2Vec(learnt_net.parameters())
infer_net = Net()
theta = Params2Vec(infer_net.parameters())
loss_fn = torch.nn.NLLLoss()
加载一个经过训练的模型(4.58MB)(准确率超过98%)。插值从随机初始化开始
所有可能的参数集可以简单使用从 0 到 1进行表示,两者的权重相加等于 1,并且由非欧几里得变换给出,𝜏:
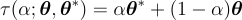
def tau(alpha, theta, theta_ast):
return alpha * theta_ast + (1 - alpha) * theta
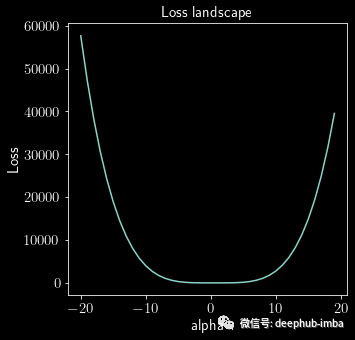
使用x 轴是一个范围从 0 到 1标量 𝛼,y 轴上的损失为 𝓛(𝛉(𝛼)),这样我们就得到了一个一维损失图。
losses = []
for alpha in torch.arange(-20, 20, 1):
for _, (data, label) in enumerate(dataloader):
with torch.no_grad():
Vec2Params(tau(alpha, theta, theta_ast), infer_net.parameters())
infer_net.eval()
prediction = infer_net(data)
loss = loss_fn(prediction, label).item()
losses.append(loss)
计算从随机集到全局优化的所有参数的损失
二维
在二维空间 [1, 2] 中绘图在原理上同样简单。给定任何随机或优化的参数集 𝛉*,我们在两个方向𝛿 和 𝜂上前进。在两个方向上,我们分别采取小步骤,𝛼 和 𝛽。因此,结果图是 𝛼 和 𝛽 的函数。
由于𝛿和𝜂是方向向量,它们代表了𝛉每个维度的方向。即,𝛿 和 𝜂 具有与 𝛉 相同的维度,它们都可以从随机高斯样本中采样。
非欧几里得变换由 𝜏 给出:
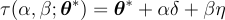
def tau_2d(alpha, beta, theta_ast):
a = alpha * theta_ast[:,None,None]
b = beta * alpha * theta_ast[:,None,None]
return a + b
然后可以从 𝛼 𝜖 [0, 1] 和 𝛽 𝜖 [0, 1] 或任何范围绘制等高线图。在下面的代码段中,两者都在 [-20, 20] 范围内。
x = torch.linspace(-20, 20, 20)
y = torch.linspace(-20, 20, 20)
alpha, beta = torch.meshgrid(x, y)
space = tau_2d(alpha, beta, theta_ast)
losses = torch.empty_like(space[0, :, :])
for a, _ in enumerate(x):
print(f'a = {a}')
for b, _ in enumerate(y):
Vec2Params(space[:, a, b], infer_net.parameters())
for _, (data, label) in enumerate(dataloader):
with torch.no_grad():
infer_net.eval()
losses[a][b] = loss_fn(infer_net(data), label).item()
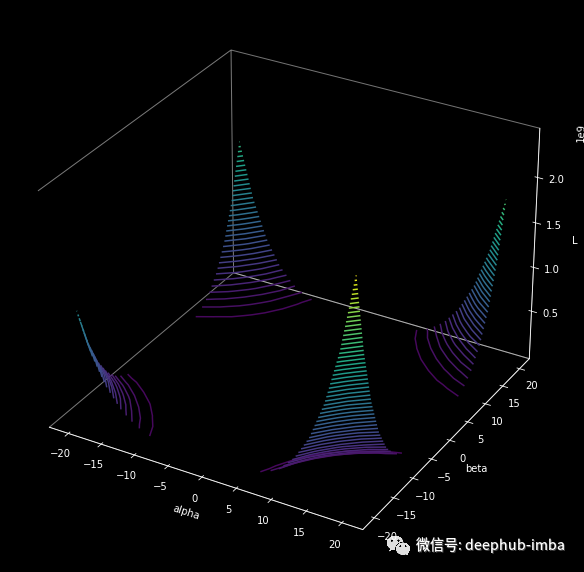
该图为我们提供了两条信息:我们可以在两个方向上移动的速率,以及用于获得更大图像的范围。上面生成等高线图的片段(来自同一个 𝛉*)用于生成下面的等高线图,唯一的区别是𝛼 和 𝛽 的范围是 [-25000, 25000] 。
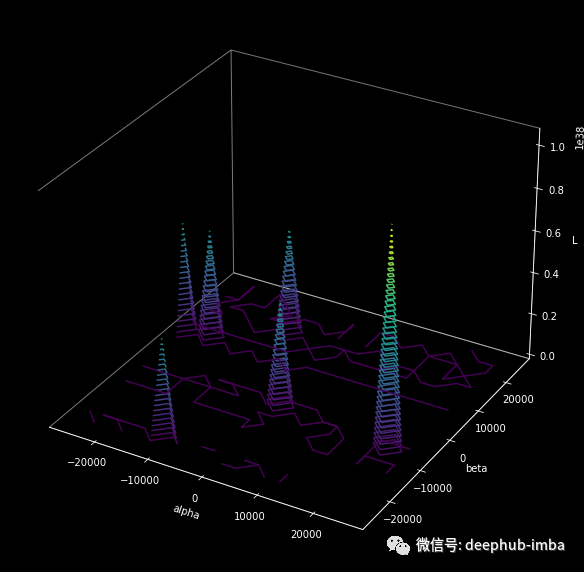
一些技巧
这种可视化在比较优化方法和网络架构时非常有用。然而这并不总是有效的,因为有一些层不会对模型的有效结果产生任何影响。例如,ReLU可能不会改变网络的行为(因为都是正数)或者像BN这样的层在网络对这些层的不变性中也同样起作用。这使得我们无法进行有意义的比较。
另一方面,在某些情况下,某些单元对网络的大权值的扰动影响很小。但是有时对同一单元的敏感权重做同样的操作可能会造成混乱。为了解决这个问题,可以将随机生成的方向向量(如𝛿)归一化,使其具有与𝛉相同的方向。更具体地说,𝛿中的每个filer与𝛉[3]中的对应层方向相同:

这样做的好处是当方向(𝛿和𝜂)以[3]的方式归一化时,等高线图能够捕捉损失表面的距离比例(例如,比较上面的两个图)。
确定解空间(solution space)区域
考虑两组经过训练的参数:𝛉ˡ 和 𝛉ˢ。前者在大BS的数据集上训练,后者在小BS上训练。两组参数的插值显示解决方案空间的宽度取决于批的大小。
例如,考虑以下轮廓从一个用 256 的批大小训练的模型 (13.74MB) 生成,而上面的一个用 64 的批大小训练的。
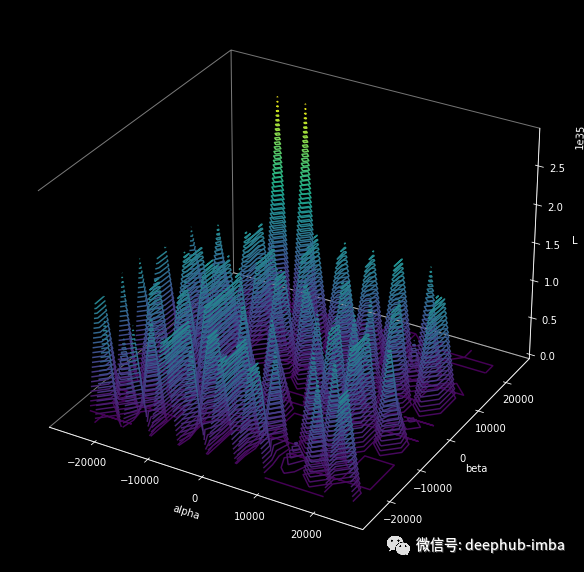
许多起伏说明,当使用大BS时,得到的权重往往小于小BS得到的权重[3]。
使用两个训练过的参数𝛉ˡ和𝛉ˢ,以下参数是插值:
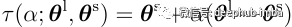
def tau_compare(alpha, theta_l, theta_s):
return theta_s + alpha * (theta_l - theta_s)
这个插值现在是一个基于批大小64到256之间的参数的函数。这种比较有助于发现更改批大小是否能够产生更好的优化。
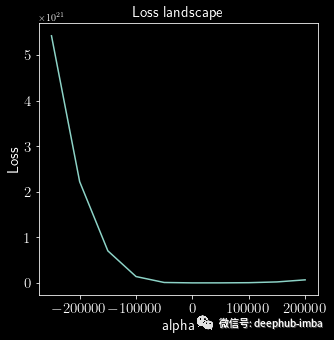
虽然这只是基于批量大小寻找好的解决方案空间的一个例子,但其他参数和超参数也可以优化。一些关键要点 [3] 包括以下内容:
- 更宽的网络可以防止混乱的局面
- 跳过连接会扩大解空间(或最小化方案)
- 空间中有浅谷会导致训练和测试的损失不理想
- 视觉上更平坦空间会对应较低的测试误差
最后这里有更详细的代码,需要的可以查看:https://github.com/tomgoldstein/loss-landscape
引用
- Ian J Goodfellow, Oriol Vinyals, and Andrew M Saxe. Qualitatively characterizing neural network optimization problems. In ICLR, 2015
- Daniel Jiwoong Im,Michael Tao, and Kristin Branson. An empirical analysis of deep network loss surfaces. arXiv:1612.04010, 2016
- Hao Li, Zheng Xu, Gavin Taylor, Christoph Studer, Tom Goldstein: Visualizing the Loss Landscape of Neural Nets. In NeurIPS, 2018
- Laurent Dinh, Razvan Pascanu, Samy Bengio, and Yoshua Bengio. Sharp minima can generalize for deep nets. In ICML, 2017
- Kenji Kawaguchi, Leslie Pack Kaelbling, and Yoshua Bengio. Generalization in deep learning. arXiv:1710.05468, 2017
作者:Sujal Vijayaraghavan
喜欢就关注一下吧:
点个 在看 你最好看!********** **********