
本质上,贝叶斯公式描述了在给定新信息的情况下如何更新我们的模型。
为了理解原因,我们将看一个简单的例子:用不公平的硬币抛硬币。假设我们有一个神奇的硬币!抛掷时可能出现正面或反面,但概率不一定相等。问题是,我们不知道确切的概率。因此,我们必须进行一些实验和统计估计才能找到答案。为了数学地表述这个问题,我们用 x 表示正面朝上的概率。
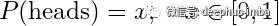
我们对 x 了解多少?🤔
此时,什么都没有。它可以是 0 到 1 之间的任何数字。
贝叶斯先验
与其将 x 视为一个固定数字,不如将其视为对实验 X 的观察。为了模拟我们对 X 的(缺乏)知识,我们选择 [0, 1] 上的均匀分布。这被称为先验,因为它表达了我们在实验之前的知识。
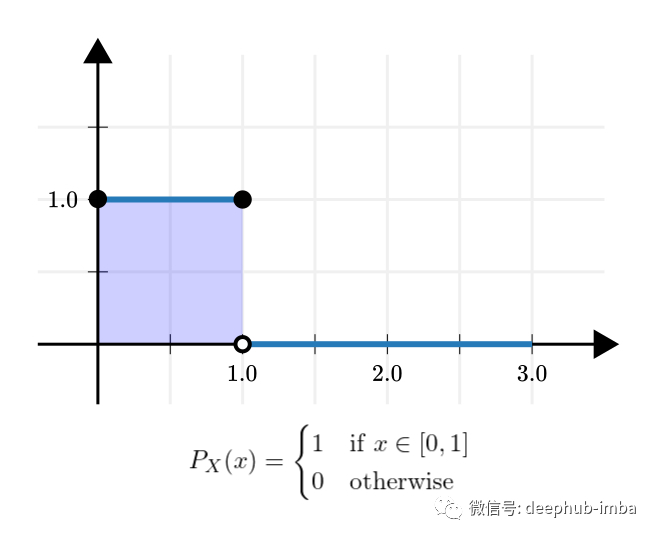
先验分布的密度,以概率形式表达我们对 X 的了解。
所以,假设我们已经扔了我们的魔法硬币,这次得到的结果是反面。它如何影响我们的硬币模型?
我们可以说,如果正面的概率是某个 x,那么我们的实验导致反面的可能性是 1-x。

注意,我们想知道条件和事件的概率分布:我们对参数的概率模型很感兴趣,因为这是我们之前的实验的结果。这被称为后验分布。
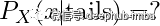
现在让我们把所有东西放在一起!
贝叶斯公式:先验后验
贝叶斯公式正是我们所需要的,因为它用先验和似然来表达后验。
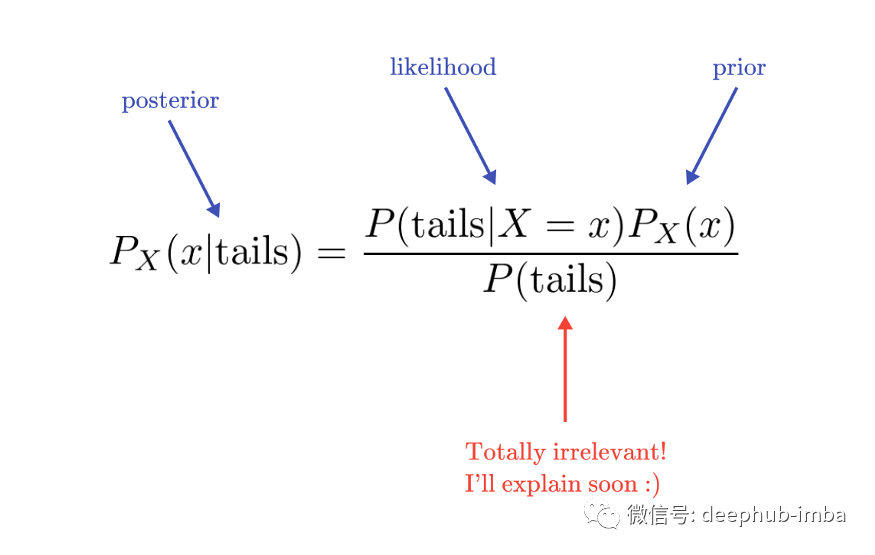
这可能令人惊讶,但实验产生反面的真实概率是无关紧要的。
为什么?因为它与 X 无关。另外,因为我们谈论的是概率分布,后验积分的计算结果为 1:

这里,反面的概率为 0.5,正如总概率定律所暗示的那样:
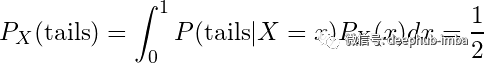
(在一般情况下,像这样的积分很难进行分析评估。)
所以,我们有我们的后验分布!请注意,它更集中在 x = 0 附近。(回想一下,x 是正面朝上的概率。)
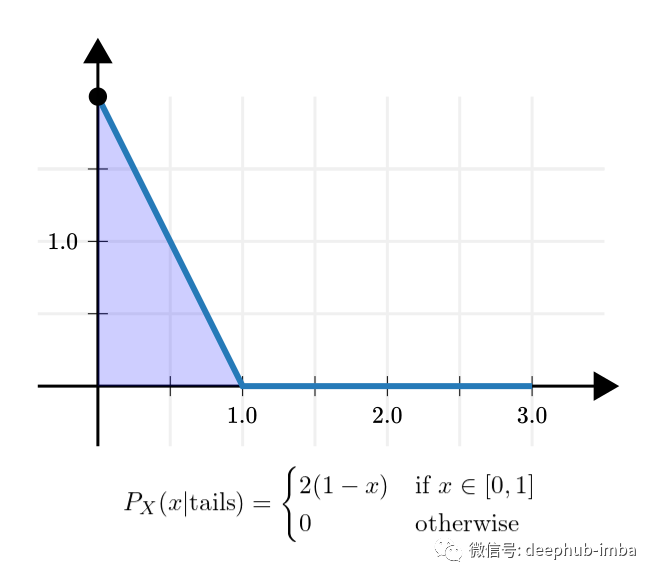
换句话说,这意味着如果我们只看到一次抛硬币导致反面,我们猜测硬币偏向于此。
当然,我们可以进行越来越多的抛硬币,这可以进一步完善后验。在 k 个正面和 n-k 个反面之后,后验将是所谓的 Beta 分布。
总结
这是最简单的贝叶斯公式解释了。
后验概率正比于先验概率乘以似然函数
或者,换句话说,贝叶斯公式描述了在给定新观察结果的情况下如何更新我们的模型。
因此,它在概率、统计和机器学习中起着基础性的作用。例如,这就是著名的均方误差的来源!
本文作者:Tivadar Danka