密码学-1-数字签名体制密码学-2-RSA签名验签方案
1 签名验签
重温上节所述的签名流程,其中散列值==>>签名(签名 ==>> 散列值)的过程中,使用私钥签名(公钥验签),这个地方涉及到了非对称加密算法,这也是非对称算法的用途之一,即数字签名。
常见用作数字签名的非对称算法:SM2(国密) 、 RSA、DSA、ECDSA(国际算法)。本文对常见的几种签名算法进行分析,内容深度只会涉及到签名流程,对于算法的具体原理实现,将会一带而过,如对算法原理有兴趣,可以私聊。
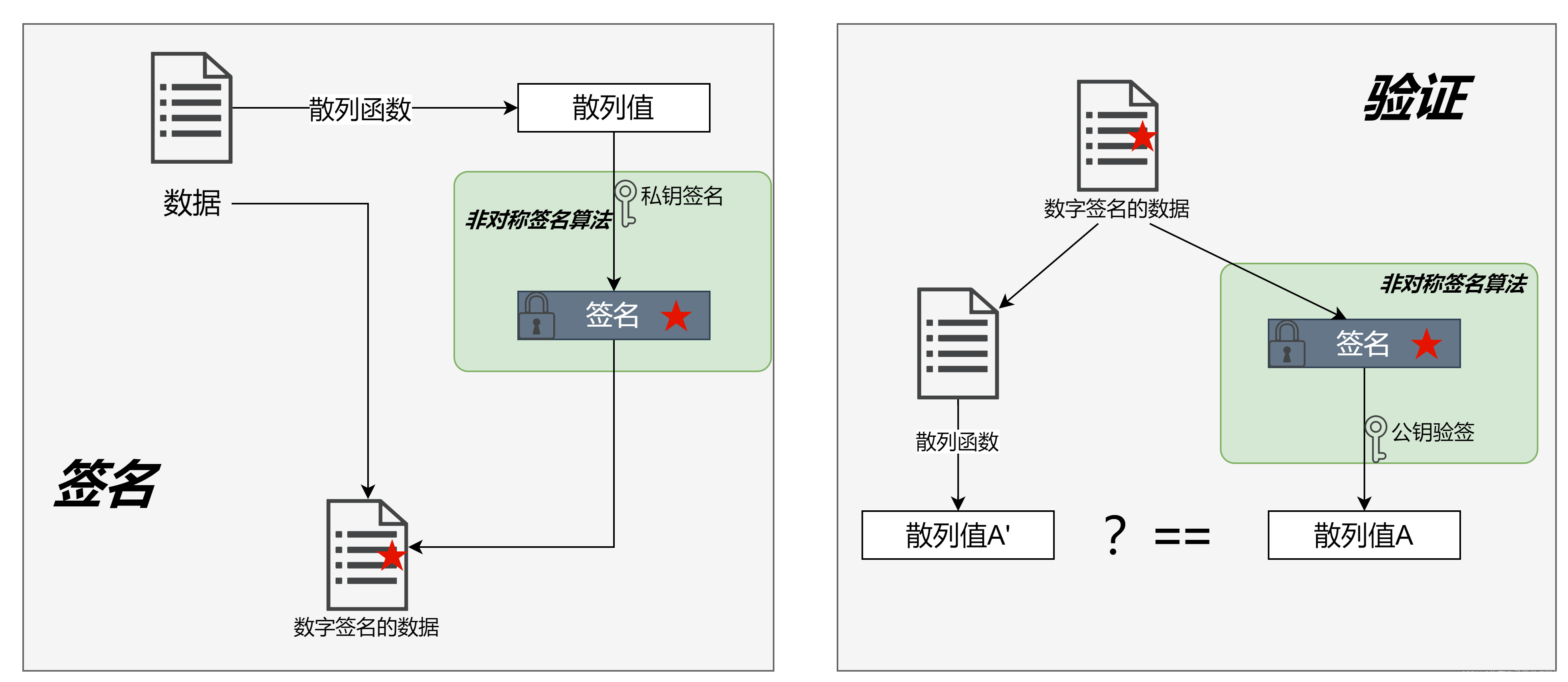
签名流程:
- 发送者对消息计算摘要值(HASH等)。
- 发送者用私钥(SM2等)对摘要值进行****签名得到签名值。(注意并不是对消息进行签名,非对称加密很慢的)
- 发送者将原始消息和签名值一同发给接收者。
验签流程
- 接收者接收到消息后,拆分出消息M和消息签名值A。
- 接收者使用公钥对拆分出的消息签名值A进行验签得到摘要值B。
- 接受者对拆分出来的消息M计算摘要值B'
- 接收者对摘要值B和**摘要值B'**进行比较,如果相同表示签名验证成功,否则就是验证失败。
2 RSA签名算法
由于RSA加密算法,相对于对称加密算法来说效率较低,目前RSA常用来加密小数据,如密钥key的加密,以及更为广泛的使用场景,签名操作。通常使用RSA私钥对消息的hash值进行签名操作,达到消息的防篡改和伪造。
2.1 RSA生成签名
用RSA生成签名的过程可用下列公式来表述:

其中:
- 发送者通过散列函数计算消息原文的散列值(hash值);
- (D,N)是签名者的私钥,签名意思就是消息原文的散列值的D次方求mod N 的结果;
- 将消息原文散列值和自己相乘D次,然后再除以N求余数,最后求得的余数就是签名;
- 生成签名之后,发送者就可以将消息原文和签名发送给接收者;
2.2 RSA验证签名
RSA的签名验证过程可用下列公式来表述:

其中:
- 接收者接收到消息 + 签名;
- (N,E)是公钥,验签就是对比签名的E次方求mod N的结果和接收消息的散列值;
- 散列值A为由签名通过RSA验签得到的数据;
- 接收者通过散列函数计算接收到的消息原文的散列值A';
- 比较A 是否等于 A',如果相等验证成功;
2.3 RSA参数的选定
2.3.1 公私钥
有一个现象很有趣,一直有人问:加密和签名,到底用的是私钥还是公钥?
其实很明显,这是对加密和签名的作用混淆了!下面将流程和作用整理出来:
即公钥加密、私钥解密、私钥签名、公钥验签。

2.3.2 E,N,D
公钥{N,E}
私钥{N,D}
2.4 RSA签名应用场景
这个问题,带入需求场景会比较容易理解一些:RSA-PSS签名算法实现,RSA-PSS(RSA概率签名)方案,被RSA实验室推荐为RSA方案中最安全的一种。
- 签名:对文件进行SHA256,得到32字节的摘要值,然后需要进行填充(PSS填充),填充之后,使用RSA的私钥进行签名
- 验签:对接收的签名使用RSA的公钥进行验签,得到原始摘要值,然后跟自己计算的摘要进行对比,通过则为合法。
2.4.1 签名
RSA-PSS填充,是在对原始数据进行hash之后,签名前,对生成的hash值进行PSS填充称为新的消息摘要EM的过程。具体实现逻辑如下:
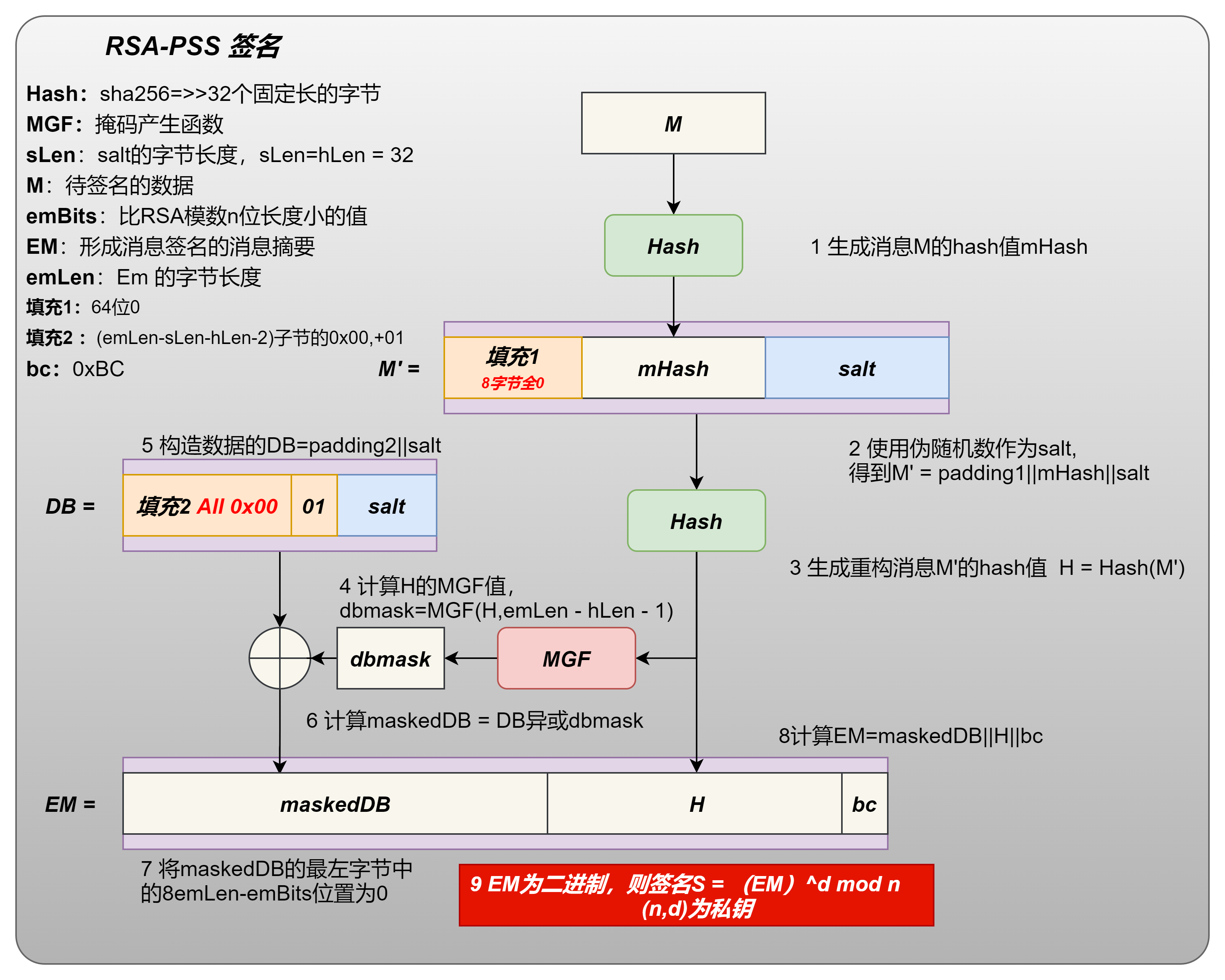
2.4.2 验签
验签的过程,是在拆解EM进行M'重构,最终通过H与H'的对比得出验签是否成功。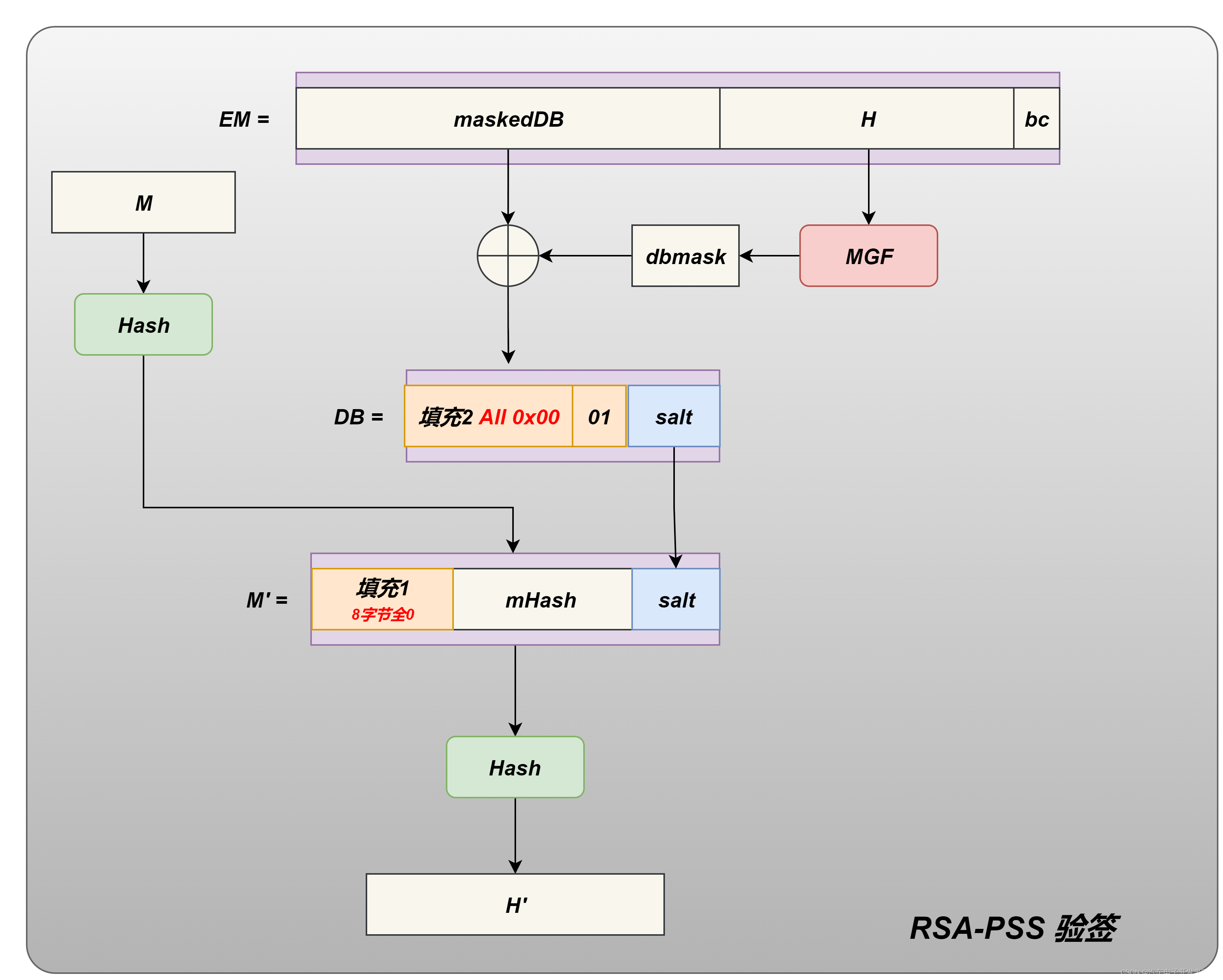
版权归原作者 汽车程序猿 所有, 如有侵权,请联系我们删除。