图注意、图卷积、网络传播都是图神经网络中消息传递的特殊情况。
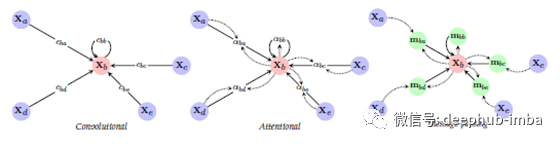
消息传递网络(MPN)、图注意力网络(GAT)、图卷积网络(GCN),甚至网络传播(NP)都是属于图神经网络(GNN)范畴的密切相关的方法。这篇文章将提供这些方法的统一视图,主要来自 [1] 中的第 5.3 章。
- NP 是 GCN 的一个特例,没有隐藏特征变换和非线性。
- GCN 是 GAT 的一个特例,“注意力”完全由图结构决定,没有节点特征。
- GAT 是 MPN 的一个特例,将隐藏特征聚合作为“消息传递”规则。
- 这些 GNN 之间的关系可以通过包含关系总结如下。
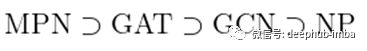
图卷积——隐藏特征的局部聚合
图卷积[2]遵循层传播规则:
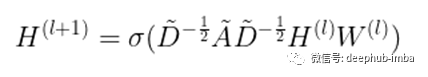
就每个节点而言,传播可以看作是相邻节点的变换 (psi) 隐藏特征 h 的局部聚合(圆加),然后是一些变换 (phi)。具体来说,在 GCN [1] 中,phi 是仿射变换 (W) 后跟非线性 (sigma)。
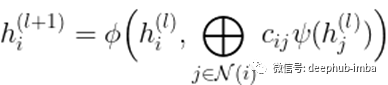
聚合量(c_{ij})完全由图结构决定,例如谱归一化邻接矩阵。
注意:聚合(circle-plus)可以是任何排列不变函数,例如求和、元素乘积等。
有趣的是,网络传播可以被视为没有任何特征转换的图卷积的特例。简而言之,遵循这里的相同符号,网络传播将遵循传播规则
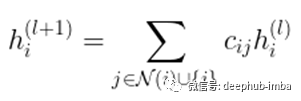
图注意力——重新学习边权重
与 GCN 类似,GAT [3] 执行隐藏特征的局部平均。但它不是仅使用图结构来指导传播,而是通过可学习的函数 alpha 学习基于隐藏特征重新加权传播权重 (c_{ij})。
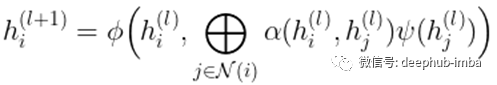
在 [3] 中,这种“自注意力机制”alpha 被计算为可学习向量 a 与两个节点的仿射变换隐藏特征的串联之间的 softmax 归一化内积。
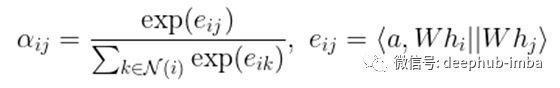
消息传递——更一般的聚合
消息传递网络 [4] 进一步概括了通过用两个节点的隐藏特征的任意函数替换隐藏特征聚合来控制聚合信息量的想法。
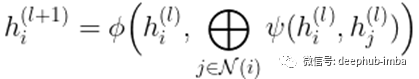
将所有不同的 GNN 方法放在一起,我们可以看到它们都遵循相同的局部聚合风格,无论是通过局部平均 (NP) 还是置换不变函数 (circle-plus)。

最后,现在更清楚了不同 GNN 之间的关系。
GCN 是通过将注意力函数 alpha 设置为谱归一化邻接矩阵来实现 GAT。
GAT是MPN的一种实现,通过self-attention作为消息传递规则进行隐藏特征聚合。
引用
[1] M. M. Bronstein, J. Bruna, T. Cohen, P. Velickovic, Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges (2021)
[2] T. N. Kipf, M. Welling, Semi-Supervised Classification with Graph Convolutional Networks (2016)
[3] P. Velickovic, G. Cucurcull, A. Casanova, A. Romero, P. Lio, Y. Bengio, Graph Attention Networks (2018)
[4] J. Gilmer, S. S. Schoenholz, P. F. Filey, O. Vinayls, G. E. Dahl, Neural Message Passing for Quantum Chemistry (2017)
[5] Network Learning — from Network Propagation to Graph Convolution
作者:Remy Lau
原文地址:https://towardsdatascience.com/a-unified-view-of-graph-neural-networks-12b40e8fdac5