有关二叉树的一些练习题

文章目录

二叉树的第三部分

这一部分 是 有关一些 二叉树 的 练习题

相同的树

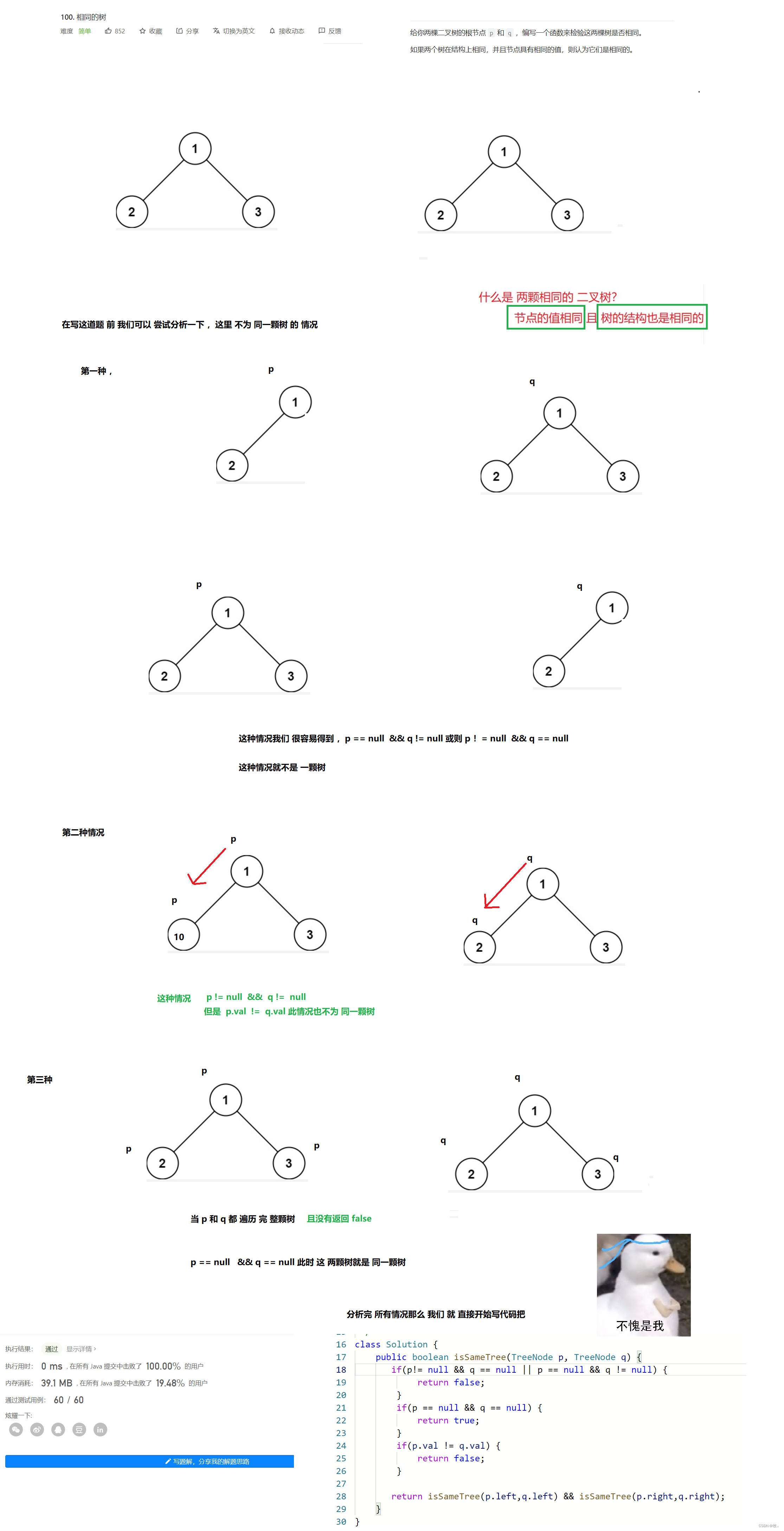
附上代码

classSolution{publicbooleanisSameTree(TreeNode p,TreeNode q){if(p!=null&& q ==null|| p ==null&& q !=null){returnfalse;}if(p ==null&& q ==null){returntrue;}if(p.val != q.val){returnfalse;}returnisSameTree(p.left,q.left)&&isSameTree(p.right,q.right);}}

时间复杂度

在来一个 小问题 这 函数 的时间复杂度 为 多少

这里我们都要遍历两颗树的结点 ，这里 需要看一下p和 q 的每棵树的结点个数

这里求 p 的 结点M 和 q 的 结点树N 的最小值

0(min(M，N))

看完了相同的 树那么接下来 来看 一道类似的题目

另一棵树的子树

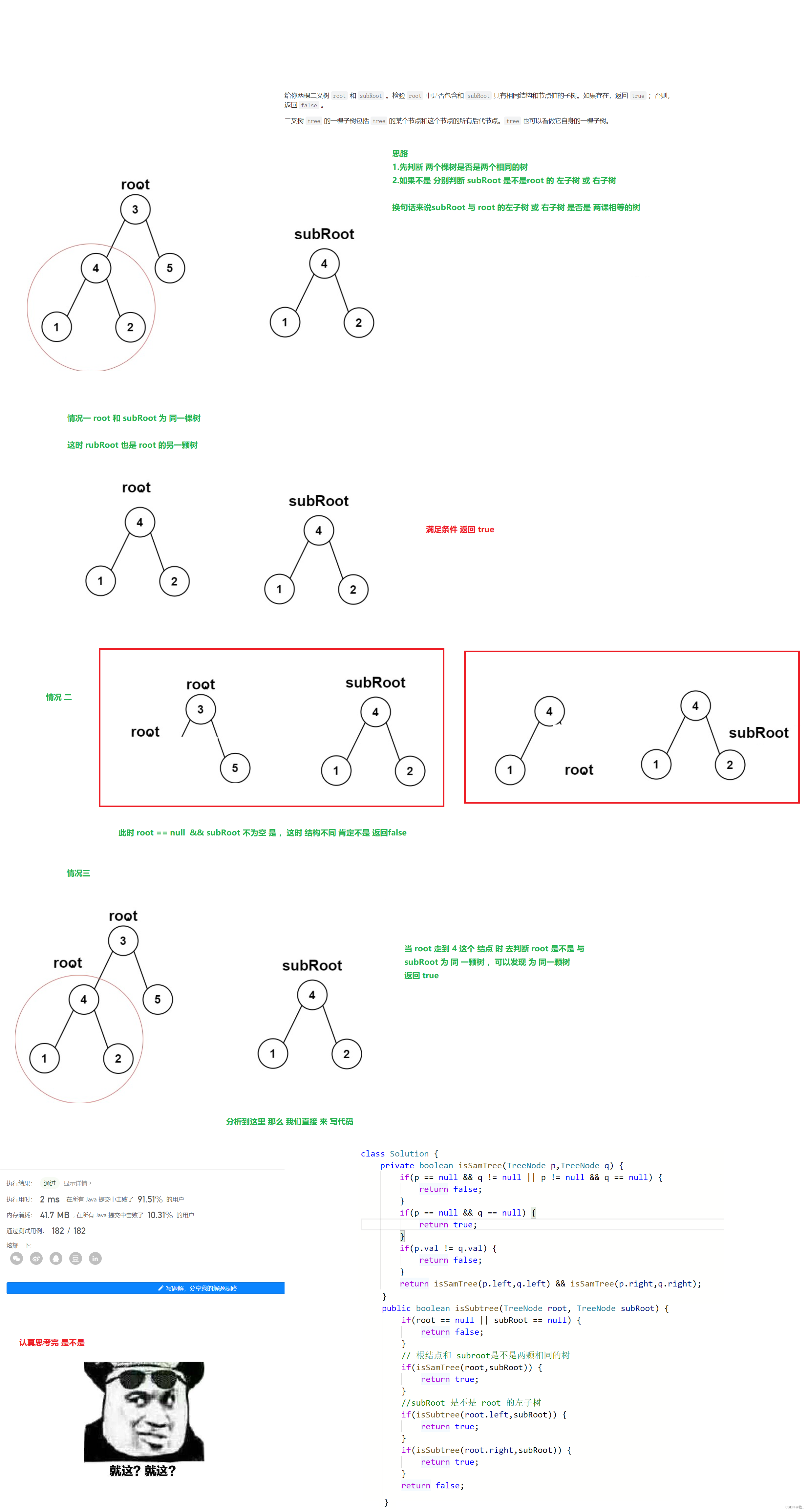
附上代码

classSolution{privatebooleanisSamTree(TreeNode p,TreeNode q){if(p ==null&& q !=null|| p !=null&& q ==null){returnfalse;}if(p ==null&& q ==null){returntrue;}if(p.val != q.val){returnfalse;}returnisSamTree(p.left,q.left)&&isSamTree(p.right,q.right);}publicbooleanisSubtree(TreeNode root,TreeNode subRoot){if(root ==null|| subRoot ==null){returnfalse;}// 根结点和 subroot是不是两颗相同的树if(isSamTree(root,subRoot)){returntrue;}//subRoot 是不是 root 的左子树if(isSubtree(root.left,subRoot)){returntrue;}if(isSubtree(root.right,subRoot)){returntrue;}returnfalse;}}

时间复杂度

这里 需要 root 的每个结点 与 subRoot 比较 所以 如果 root 有 S 个结点 subRoot 有 T 个结点，每个 S都需要去 T 比较

所以时间复杂度 就为0(S * N)

平衡二叉树

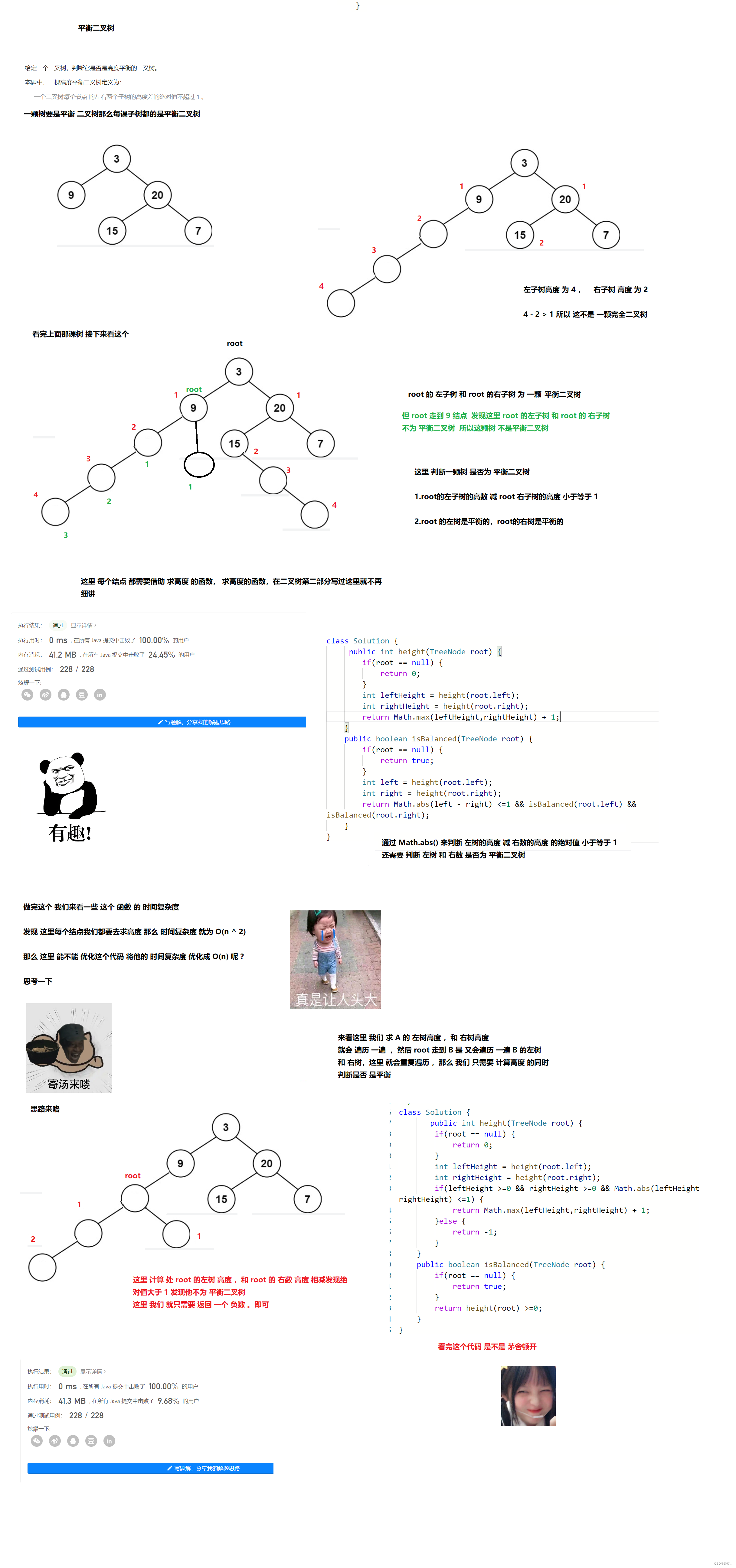
附上代码

classSolution{publicintheight(TreeNode root){if(root ==null){return0;}int leftHeight =height(root.left);int rightHeight =height(root.right);returnMath.max((leftHeight+1),(rightHeight+1));}// 判断连个树是否为 平衡二叉树publicbooleanisBalanced(TreeNode root){if(root ==null){returntrue;}int left =height(root.left);int right =height(root.right);returnMath.abs(left - right)<=1&&isBalanced(root.left)&&isBalanced(root.right);}}

优化后

classSolution{publicintheight(TreeNode root){if(root ==null){return0;}int leftHeight =height(root.left);int rightHeight =height(root.right);if(leftHeight >=0&& rightHeight >=0&&Math.abs(leftHeight - rightHeight)<=1){returnMath.max(leftHeight,rightHeight)+1;}else{return-1;}}publicbooleanisBalanced(TreeNode root){if(root ==null){returntrue;}returnheight(root)>=0;}}

对称二叉树

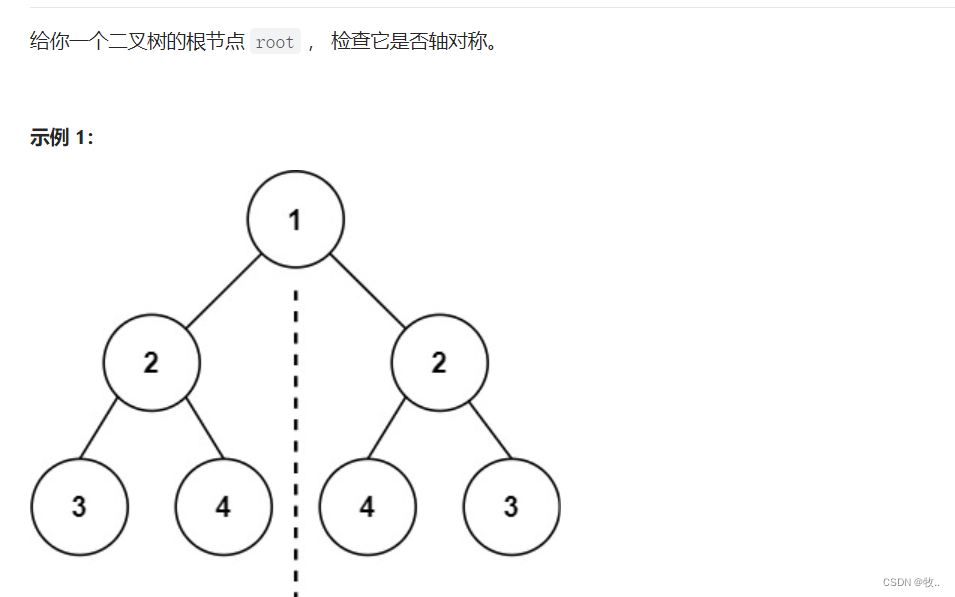
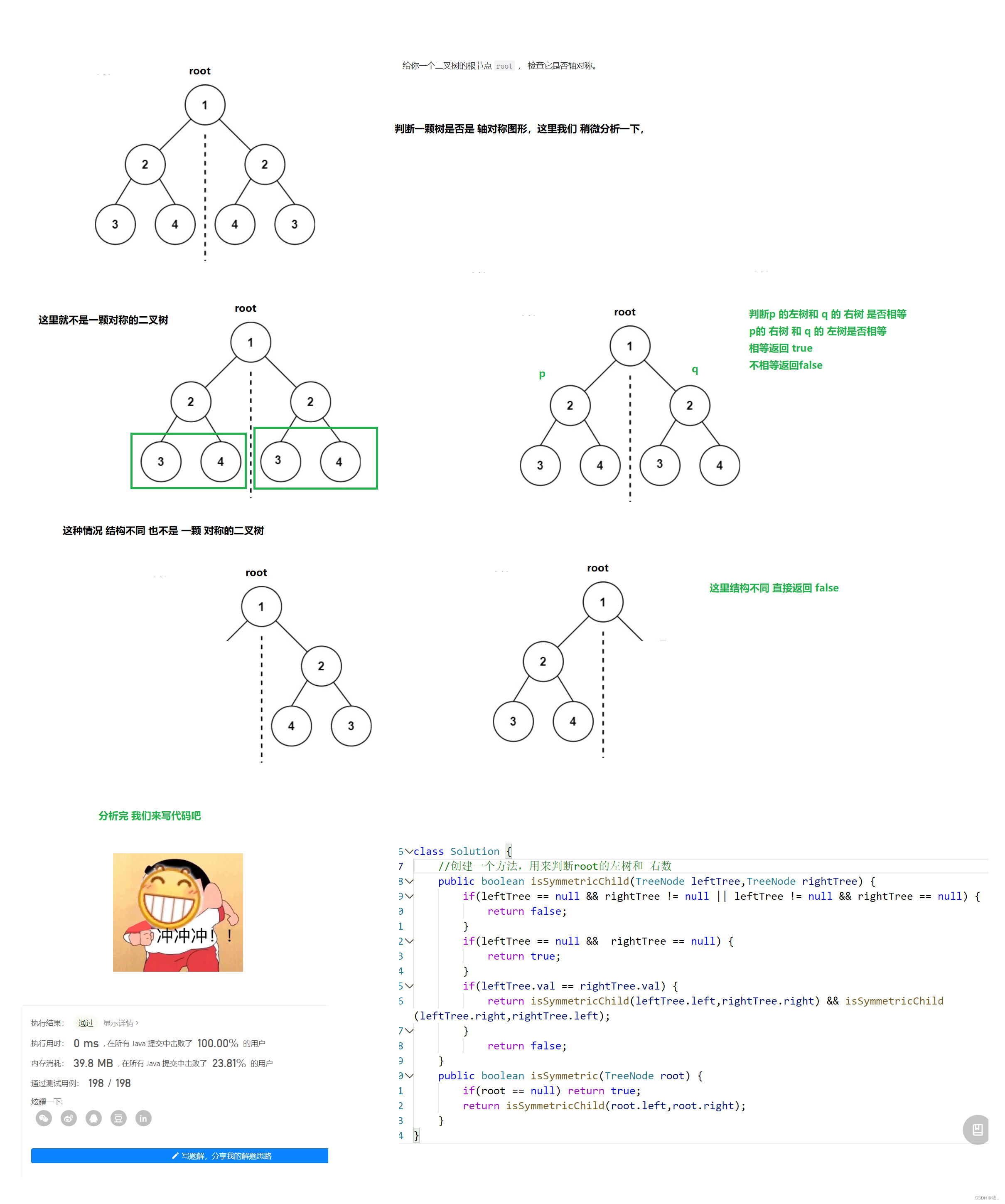
附上代码

classSolution{//创建一个方法，用来判断root的左树和 右数publicbooleanisSymmetricChild(TreeNode leftTree,TreeNode rightTree){if(leftTree ==null&& rightTree !=null|| leftTree !=null&& rightTree ==null){returnfalse;}if(leftTree ==null&&rightTree ==null){returntrue;}if(leftTree.val == rightTree.val){returnisSymmetricChild(leftTree.left,rightTree.right)&&isSymmetricChild(leftTree.right,rightTree.left);}returnfalse;}publicbooleanisSymmetric(TreeNode root){if(root ==null)returntrue;returnisSymmetricChild(root.left,root.right);}}

创建一颗二叉树

回忆上面我们创建一颗二叉树是不是 通过 穷举 来创建的一颗二叉树，那么 现在我们来使用先序遍历来创建一颗二叉树

二叉树遍历

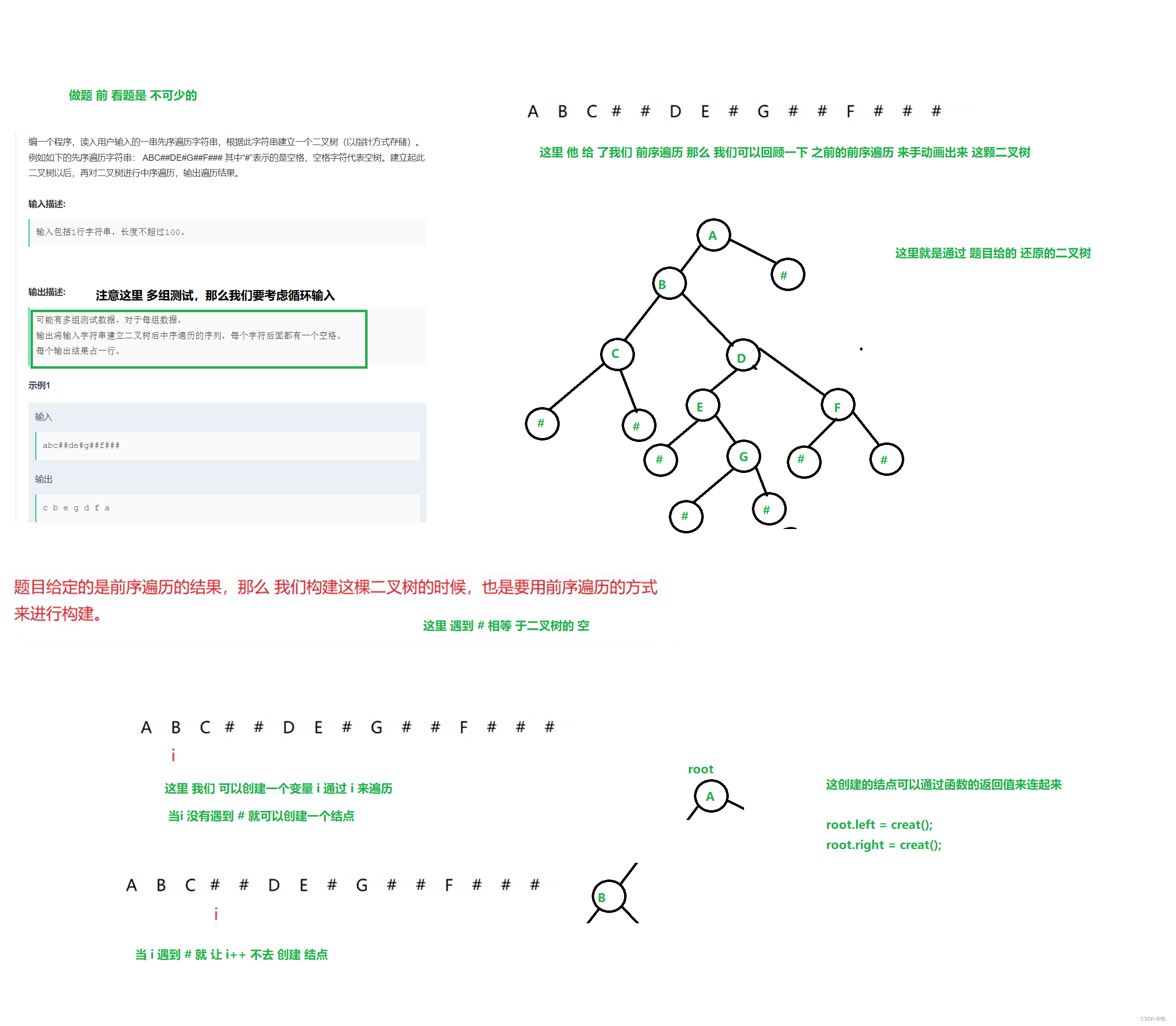
附上代码

importjava.util.Scanner;importjava.util.*;classTreeNode{publicchar val;publicTreeNode left;publicTreeNode right;publicTreeNode(char val){this.val = val;}}publicclassMain{publicstaticint i=0;publicstaticTreeNodecreateTree(String str){TreeNode root =null;if(str.charAt(i)!='#'){
            root =newTreeNode(str.charAt(i));
            i++;
            root.left =createTree(str);
            root.right =createTree(str);}else{
            i++;}return root;}publicstaticvoidinorter(TreeNode root){if(root ==null){return;}inorter(root.left);System.out.print(root.val+" ");inorter(root.right);}publicstaticvoidmain(String[] args){Scanner sc =newScanner(System.in);// 这里需要注意hasNext 与 hasNextLine 的区别// hasNextLine 遇到空格不结束// hasNext 遇到空格结束while(sc.hasNextLine()){String str = sc.nextLine();TreeNode root =createTree(str);inorter(root);}

​ 最后来补充一下之前的程序 遍历 ，回忆一下 上文 写 的 判断一颗完全二叉树

其实程序遍历也是 这个思路 通过 一个队列，为空 就 不 加入队列，

程序遍历

// 程序遍历publicvoidlevelOrder(TreeNode root){if(root ==null){return;}Queue<TreeNode> queue =newLinkedList<>();
        queue.offer(root);while(!queue.isEmpty()){TreeNode tmp = queue.poll();System.out.print(tmp.val+" ");if(tmp.left!=null){
                queue.offer(tmp.left);}if(tmp.right !=null){
                queue.offer(tmp.right);}}}

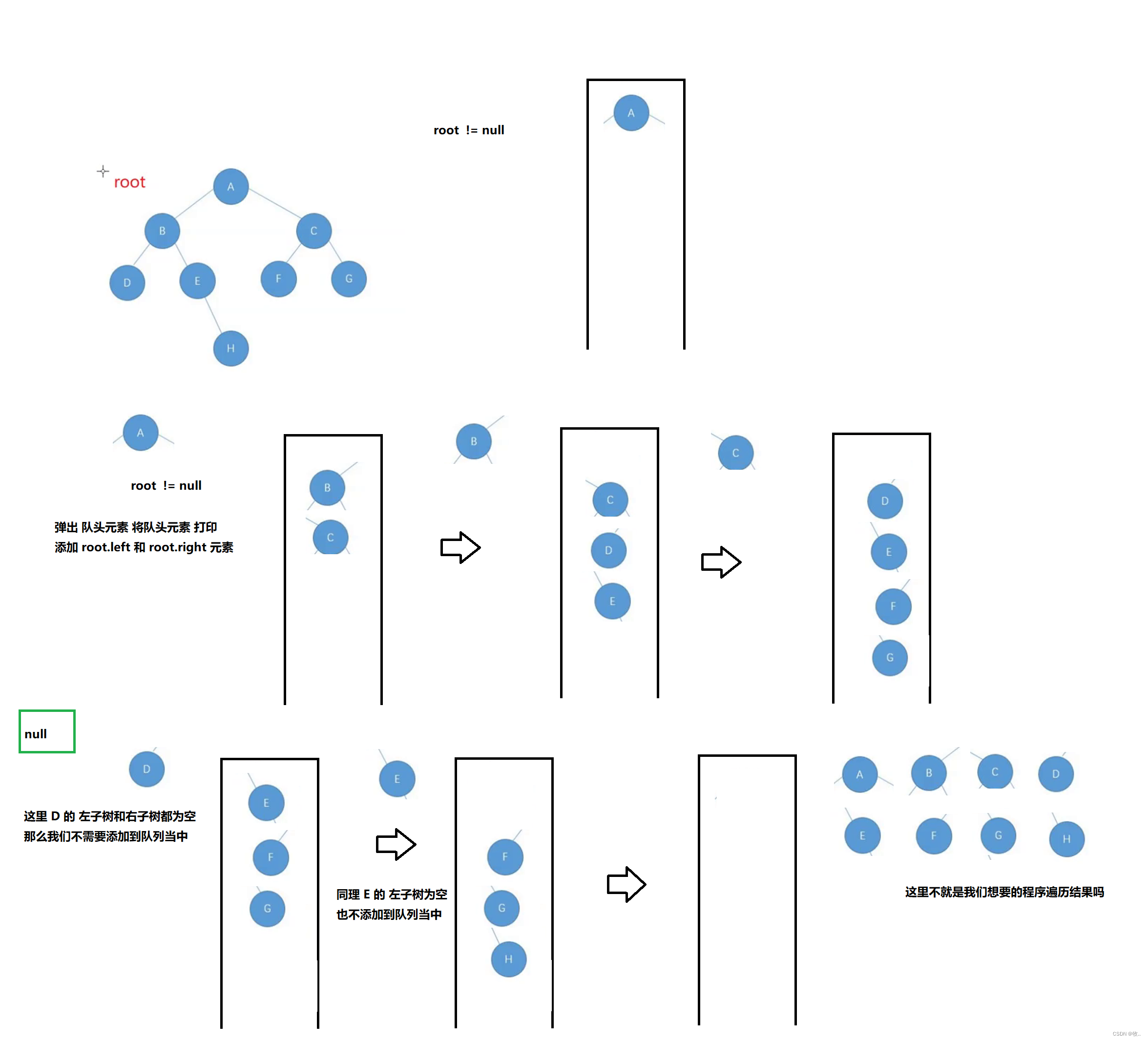
写 完了 程序遍历那么我们上 力扣 上写一下oj题嘿嘿

二叉树的层序遍历

classSolution{publicList<List<Integer>>levelOrder(TreeNode root){List<List<Integer>> list =newArrayList<>();Queue<TreeNode> queue =newLinkedList<>();
        queue.offer(root);if(root ==null)return list;while(!queue.isEmpty()){int size = queue.size();List<Integer> list2 =newArrayList<>();while(size !=0){TreeNode tmp = queue.poll();
                list2.add(tmp.val);if(tmp.left !=null){
                    queue.offer(tmp.left);}if(tmp.right !=null){
                    queue.offer(tmp.right);}
                size--;}
            list.add(list2);}return list;