CSDN上看了很多文章,但是我感觉写的太过专业化,很多时候读起来很费力气,明明是简单的过程,但是经过复杂的说法,很难使人一读就懂。经过深入的思考,以及算法报告是对学生理解能力的考核,我认为加密算法这么写更易懂,同样体现了对这个知识点的学习和思考:那么开始吧,首先我们要明白几个置换过程,这个和加密算法无关,你只需要明白这个置换即可。
1、几个基本概念
第一个置换是:初始置换-终止置换-IP置换-初始置换IP
虽然我写了四个置换,是因为很多专业的人用了不同的称呼,但他们的方法都是一样的原来是64位的,置换后依然是64位的,所以看到这三个,你就想着这是把原数据打乱了,怎么置换呢,首先按照需要加密双方的约定指定一张表,这张表写着64位数字,代表着咱们要加密的64位原文,比如我和另一个要给他发消息的人约定了如下表格:
58,50,42,34,26,18,10,2,
60,52,44,36,28,20,12,4,
62,54,46,38,30,22,14,6,
64,56,48,40,32,24,16,8,
57,49,41,33,25,17, 9,1,
59,51,43,35,27,19,11,3,
61,53,45,37,29,21,13,5,
63,55,47,39,31,23,15,7,
我们有64位数据,此时将输入的64位明文的第1位置换到第40位,第2位置换到第8位,第3位置换到第48位。以此类推,最后一位是原来的第7位。置换规则是规定的。
此时我将得到经过置换的64位数据。
第二个置换:扩展置换(32位到48位)
这个32位怎么来的不用管,先理解怎么置换的,我把这32位数据分为8组,每组我就有4个,如下:

每组的4位,我们规定让他用一种方法变成6位,怎么变呢?
把每组的最后一个数字补到前一组的开头,像拉火车一样,车尾接车头,形成如下的48位数据:

第三个置换:压缩置换(S盒48位到32位)
同样48位怎么来的,先不管,看看置换方法:
我和那个人收我消息的人规定的另一张表是用在这的,这表我俩称之为S盒,而且我俩一起做了8张,每张有4行16列,共64个方框。
我们将要压缩的48位分为8组,每组6位,这6位二进制数,掐头去尾,将拿出来的这两个数组成一个新的数字,转为十进制,作为我和那个人规定的S盒这张表的行数。中间的四个数字转为十进制,作为列数。行列确定了表中的一个加密数字。当然四个二进制数最大的是1111,就是十进制15,所以我俩规定的这张表有重复数字,但是最大数字是15。这样6位数字,变成了表中的一个数字,且它最大是1111,共计8组,68变成了48。
第四个运算:循环左移(位数不变)
左移比较简单,就是循环左移,头尾相接,进行移动,但我俩规定第一次左移要移动一个位置,其中第一次、第二次、第九次、第十六次是循环左移一位,其他都是左移两位。
第五个置换:置换选择pc-1(64位到56位)
置换选择就是置换后,选择一种方式读取。我俩还有张表,叫这个名字--缩小选择换位表1(置换选择表1)。
将64位数据,分为8组,每组8个,是不是这样的:

表里有64个数据,但是最后一位我们不要,前七位留着,但不是按照正常的方式读取,现在我们从下到上读取,读取的过程中,我们给他分为两组,C0和D0,C0是左边蓝色的部分,拿走28位,D0不仅从下往上,还要从右往左,再拿走28位。
第六个置换:压缩置换pc-2(56位到48位)
这次的表你猜对了,还是我们规定的,同样的压缩,但这是表2。位数不同,所以方法不同,因为这部分会用在子密钥上,所以加了个pc。
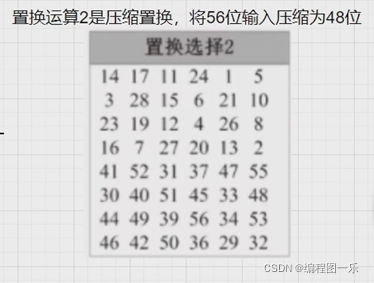
这次我们规定上图表中的56位数据,第9、18、22、25、35、38、43、54这8位被剔除了,这样就压缩到了48位。
第七个运算:F变换
F变换是一个运算流程的统称,这是过程是将32位数据扩展置换到48位,这48位与pc-2置换后的48位进行异或运算(异或运算两个数相同结果为0,不同为1),经过F变换后,还是48位数据。
第八个置换:P-盒置换(48bit到32bit)
S-盒代替运算,每一盒得到4位,8盒共得到32位输出。这32位输出作为P盒置换的输入块。P盒置换将每一位输入位映射到输出位。任何一位都不能被映射两次,也不能被略去。经过P-盒置换的结果与最初64位分组的左半部分异或,然后左右两部分交换,开始下一轮迭代。
P-盒置换表(表示数据的位置)共32位。将32位的输入的第16位放在第一位,第七位放在第二位,第二十位放在第三位,以此类推。如下:
16
7
20
21
29
12
28
17
1
15
23
26
5
18
31
10
2
8
24
14
32
27
3
9
19
13
30
6
22
11
4
25
第九个置换:逆置换
将初始置换进行16次的迭代,即进行16层的加密变换,这个运算过程我们暂时称为函数f。得到L16和R16,将此作为输入块,进行逆置换得到最终的密文输出块。逆置换是初始置换的逆运算。从初始置换规则中可以看到,原始数据的第1位置换到了第40位,第2位置换到了第8位。则逆置换就是将第40位置换到第1位,第8位置换到第2位。以此类推,逆置换规则如下。
40
8
48
16
56
24
64
32
39
7
47
15
55
23
63
31
38
6
46
14
54
22
62
30
37
5
45
13
53
21
61
29
36
4
44
12
52
20
60
28
35
3
43
11
51
19
59
27
34
2
42
10
50
18
58 26
33
1
41
9
49
17
57
25
注:DES算法的加密密钥是根据用户输入的秘钥生成的,该算法把64位密码中的第8位、第16位、第24位、第32位、第40位、第48位、第56位、第64位作为奇偶校验位,在计算密钥时要忽略这8位.所以实际中使用的秘钥有效位是56位。秘钥共64位,每次置换都不考虑每字节的第8位,因为这一位是奇偶校验位,所以64位秘钥的第8、16、24、32、40、48、56、64位在计算秘钥时均忽略。
2、子密钥生成过程
明文64位-> 初始置换 -> pc-1置换选择(56bit) -> 分组C0、D0(每组28bit)->两组都循环左移 -> pc-2压缩置换(48bit),生成了子密钥key1(48bit)
由于我们需要16轮变换,也称之为“轮操作”。这个k1要和R0做异或运算,即F变换。得到的48位结果进入S1盒压缩处理,为32位,和L0交换顺序后的64位密文,是我们下一次循环pc-1置换选择的初始值。
根据轮数,将Cn和Dn分别循环左移1位或2位。
循环左移每轮移动的位数如下:

3、des加密过程(迭代)
明文64位->初始置换-> 分组 -> S盒压缩处理(16轮) -> 逆初始置换IP-1-> 密文
比如我有一句话要传送给收件人 I love you,yy
首先使用ascii(电脑编码系统),进入计算机后为二进制,如图:
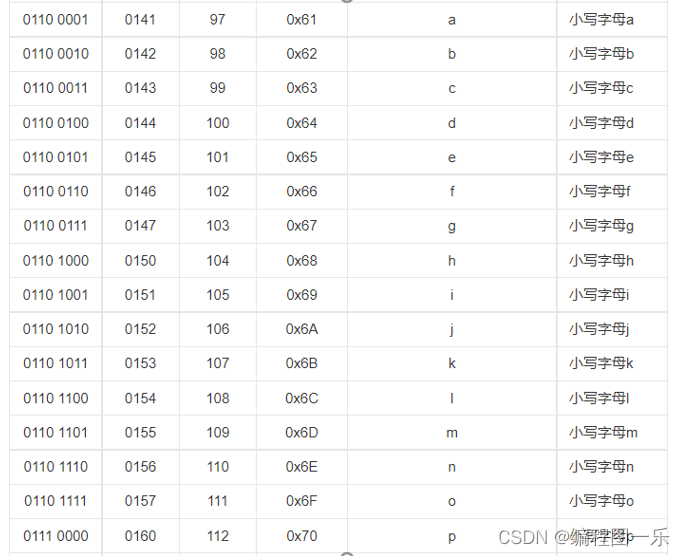
存入计算机为:0110 1001(i) 0010 0001(空格) 0110 1100(l) 0110 1111(o) 0111 0110(v) 0110 0101(e) 0010 1100(逗号) 0111 1001(y) 0111 1001(y)
(这里没有考虑数据类型,比如一般int占4个字节,以及物理层传输时的比特流的编码)
共计9个字符。每个1字节,即8位,共计72位,此时,我们将数据分为多组,每组64位,即我们只要前64位来演示des加密后的密文。目前我们有64bit的明文。
64bit的明文首先要按照表3-2进行IP置换,即原始数据的58位放在新数据的第1位,原始数据的第50位放在新数据第2位,以此类推。得到新的64bit数据分成L0 和R0 左右两部分,每部分为32bit。

首先对原始数据整理一下:
序号 1
0110 1001(i)
2
0010 0001(空格)
3
0110 1100(l)
4
0110 1111(o)
5
0111 0110(v)
6
0110 0101(e)
7
0010 1100(逗号)
8
0111 1001(y)
(好多啊,好麻烦吖,开始考虑这项任务有没有必要了)
这里只置换两行举例:
序号 1
1011 1101
2
1001 0000
由此我们得到置换后的64bit数据。
将此分为L0(32bit)和R0(32bit),R0与秘钥结合(异或运算)后,进行S1盒压缩处理,处理后的数据为32位继续作为R0,与秘钥结合,而原来的R0赋值给L0,即:原来的右半部分成为新的左半部分。用式子表示如下:
Ln = R(n - 1);(不存在R负1)
Rn = L(n - 1)⊕f(Rn-1,kn-1)
[⊕:异或运算 Kn是向第N层输入的48位的秘钥,f是以Rn-1和Kn为变量的输出32位的函数]
如此16轮后,数据依然是64bit,而右半部分的R0由几步运算构成:扩展置换(32bit->48bit);秘钥置换(Kn的生成,n=0~16);S-盒压缩处理替代;P-盒置换,最后还有交换和逆置换,完成输入密文的任务。
4、子密钥算法的流程图

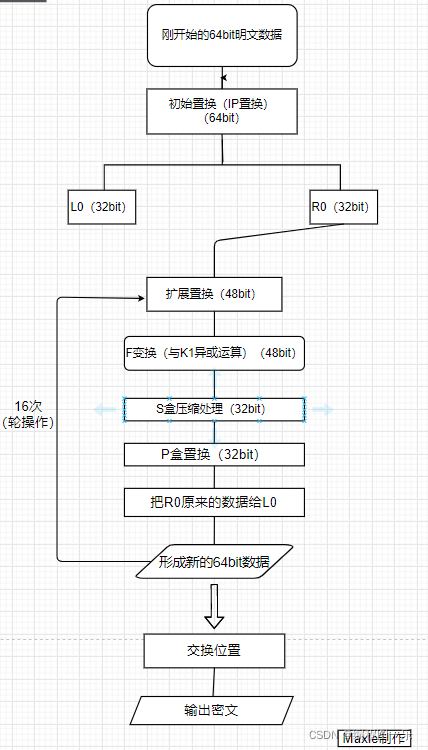
5、加密算法流程图
版权归原作者 编程图一乐 所有, 如有侵权,请联系我们删除。