介绍
无论多么强大,机器学习都无法预测一切。例如与时间序列预测有关的领域中,表现得就不是很好。
尽管有大量自回归模型和许多其他时间序列算法可用,但如果目标分布是白噪声或遵循随机游走,则无法预测目标分布。
因此,您必须在进一步努力之前检测此类分布。
在本文中,您将了解什么是白噪声和随机游走,并探索经过验证的统计技术来检测它们。
关于自相关的简要说明
自相关涉及找到时间序列与其自身滞后版本之间的相关性。考虑这个分布:
deg_C = tps_july["deg_C"].to_frame("temperature")
deg_C.head()

滞后时间序列意味着将其向后移动 1 个或多个周期:
deg_C["lag_1"] = deg_C["temperature"].shift(periods=1)
deg_C["lag_2"] = deg_C["temperature"].shift(periods=2)
deg_C["lag_3"] = deg_C["temperature"].shift(periods=3)
deg_C.head(6)
自相关函数 (ACF) 在每个滞后 k 处找到时间序列与其滞后版本之间的相关系数。您可以使用 statsmodels 中的 plot_acf 函数绘制它。这是它的样子:
from matplotlib import rcParams
from statsmodels.graphics.tsaplots import plot_acf
rcParams["figure.figsize"] = 9, 4
# ACF function up to 50 lags
fig = plot_acf(deg_C["temperature"], lags=50)
plt.show();

XAxis 是滞后 k,YAxis 是每个滞后的 Pearson 相关系数。红色阴影区域是置信区间。如果条形的高度在该区域之外,则意味着相关性在统计上是显着的。
什么是白噪声?
简而言之,白噪声分布是具有以下特征的任何分布:
- 零均值
- 恒定的方差/标准偏差(不随时间变化)
- 所有滞后的零自相关
本质上,它是一系列随机数,根据定义,没有算法可以合理地对其行为进行建模。
有特殊类型的白噪声。如果噪声是正态的(服从正态分布),则称为高斯白噪声。让我们直观地看一个例子:
noise = np.random.normal(loc=0, scale=0.5, size=1000)
plt.figure(figsize=(12, 4))
plt.plot(noise);

即使偶尔出现尖峰,也看不到明显的模式,即分布是完全随机的。
验证这一点的最佳方法是创建 ACF 图:
fig = plot_acf(noise, lags=40)
plt.title("Autocorrelation of a White Noise Series")
plt.show()
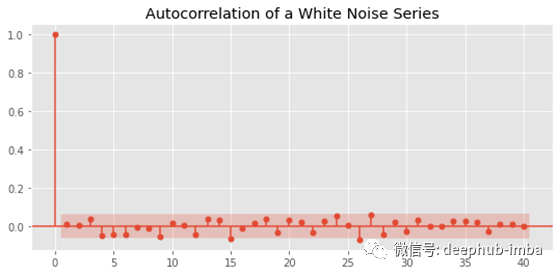
还有“严格”的白噪声分布——它们的序列相关性严格为 0。这与棕色/粉红色噪声或其他自然随机现象不同,其中存在弱序列相关但仍保持无记忆。
白噪声在预测和模型诊断中的重要性

尽管白噪声分布被认为是死胡同,但它们在其他情况下也非常有用。
例如,在时间序列预测中,如果预测值和实际值之间的差异代表白噪声分布,您可以为自己的工作做得很好而感到欣慰。
当残差显示任何模式时,无论是季节性的、趋势的还是非零均值,这表明仍有改进的空间。相比之下,如果残差是纯白噪声,则您将所选模型的能力最大化。
换句话说,该算法设法捕获了目标的所有重要信号和属性。剩下的是无法归因于任何事物的随机波动和不一致的数据点。
例如,我们将使用七月 Kaggle 操场比赛来预测空气中一氧化碳的含量。我们将保留输入“原样”——我们不会执行任何特征工程,我们将选择一个具有默认参数的基线模型:
preds = forest.predict(X_test)
residuals = y_test.flatten() - preds
plt.plot(residuals)
plt.title("Plot of the Error residuals");

fig = plot_acf(residuals, lags=50)
plt.title("Autocorrelation Plot of the Error residuals")
plt.show();
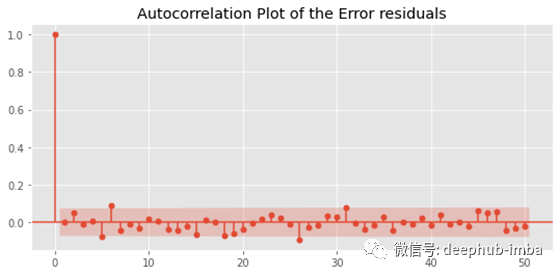
ACF 图中有一些模式,但它们在置信区间内。这两个图表明,即使使用默认参数,随机森林也可以从训练数据中捕获几乎所有重要信号。
随机游走
时间序列预测中更具挑战性但同样不可预测的分布是随机游走。与白噪声不同,它具有非零均值、非常量标准/方差,并且在绘制时看起来很像正则分布:
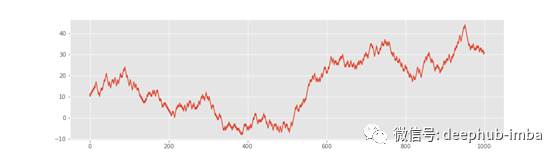
随机游走系列总是以这种方式巧妙地伪装,但它们仍然是不可预测的。对今天数值的最佳猜测是昨天的数值。
初学者常见的困惑是将随机游走视为简单的随机数序列。情况并非如此,因为在随机游走中,每一步都依赖于前一步。
因此,随机游走的自相关函数确实返回非零相关。
随机游走的公式很简单:

无论之前的数据点是什么,都可以为其添加一些随机值,并根据需要继续。让我们用 Python 生成它,起始值为 99:
walk = [99]
for i in range(1000):
# Create random noise
noise = -1 if np.random.random() < 0.5 else 1
walk.append(walk[-1] + noise)
rcParams["figure.figsize"] = 14, 4
plt.plot(walk);

让我们也绘制 ACF:
fig = plot_acf(walk, lags=50)
plt.show();

如您所见,前 40 个滞后产生统计上显着的相关性。
那么,当可视化不是一种选择时,我们如何检测随机游走?
由于它们的创建方式,时间序列的差分应该隔离每个步骤的随机添加。通过将序列滞后 1 并从原始值中减去它来获取一阶差分。Pandas 有一个方便的 diff 函数来做到这一点:
walk_diff = pd.Series(walk).diff()
plt.plot(walk_diff);
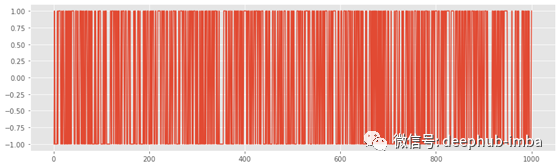
如果绘制时间序列的一阶差分并且结果是白噪声,则它是随机游走。
带有漂移的随机游走
对常规随机游走的一个轻微修改是在随机步骤添加一个称为漂移的常数值:

Drift 通常用 μ 来表示,就随时间变化的值而言,漂移意味着逐渐变成某种东西。
例如,即使股票不断波动,它们也可能有正漂移,即随着时间的推移整体逐渐增加。
现在,让我们看看如何在 Python 中模拟这一点。我们将首先创建起始值为 25 的常规随机游走:
walk = [25]
for i in range(1000):
# Create random noise
noise = -1 if np.random.random() < 0.5 else 1
walk.append(walk[-1] + noise)
从上面的公式中,我们看到我们需要在每一步添加所需的漂移。让我们添加 5 的漂移并查看绘图:
drift = 5
drifty_walk = pd.Series(walk) + 5
drifty_walk.plot(title="A Random Walk with Drift");

尽管波动剧烈,但该系列仍有明显的上升趋势。如果我们执行差分,我们将看到该系列仍然是随机游走:
drifty_walk.diff().plot();
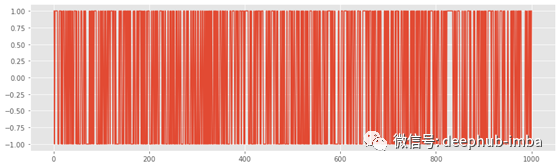
统计检测随机游走
您可能会问,是否有更好的方法来识别随机游走,而不仅仅是从图中“观察”它们。
作为答案,Dicker D. A. 和 Fuller W. A. 在 1979 年概述了一个假设检验,它被称为增广 Dickey-Fuller 检验。
本质上,它试图检验一系列遵循随机游走的零假设。在幕后,它对滞后价格的价格差异进行回归。
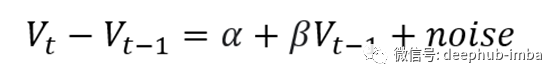
如果找到的斜率 (β) 等于 0,则该系列是随机游走。如果斜率显着不同于 0,我们拒绝该系列遵循随机游走的原假设。
幸运的是,您不必担心数学问题,因为该测试已经在 Python 中实现了。
我们从 statsmodels 导入 adfuller 函数,并将其用于上一节中创建的漂移随机游走:
from statsmodels.tsa.stattools import adfuller
results = adfuller(drifty_walk)
print(f"ADF Statistic: {results[0]}")
print(f"p-value: {results[1]}")
print("Critical Values:")
for key, value in results[4].items():
print("\t%s: %.3f" % (key, value))
----------------------------------------------
ADF Statistic: -2.0646595557153424
p-value: 0.25896047143602574
Critical Values:
1%: -3.437
5%: -2.864
10%: -2.568
我们查看 p 值,约为 0.26。由于 0.05 是显着性阈值,我们无法拒绝drifty_walk 是随机游走的零假设,即它是随机游走。
让我们对我们知道不是随机游走的分布进行另一个测试。我们将使用 TPS 七月 Kaggle 游乐场比赛中的一氧化碳目标:
results = adfuller(tps_july["target_carbon_monoxide"])
print(f"ADF Statistic: {results[0]}")
print(f"p-value: {results[1]}")
print("Critical Values:")
for key, value in results[4].items():
print("\t%s: %.3f" % (key, value))
---------------------------------------------------
ADF Statistic: -8.982102584771997
p-value: 7.26341357249666e-15
Critical Values:
1%: -3.431
5%: -2.862
10%: -2.567
p 值非常小,这表明我们可以轻松拒绝 target_carbon_monoxide 遵循随机游走的原假设。
本文作者:Bex T.