文章目录
121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
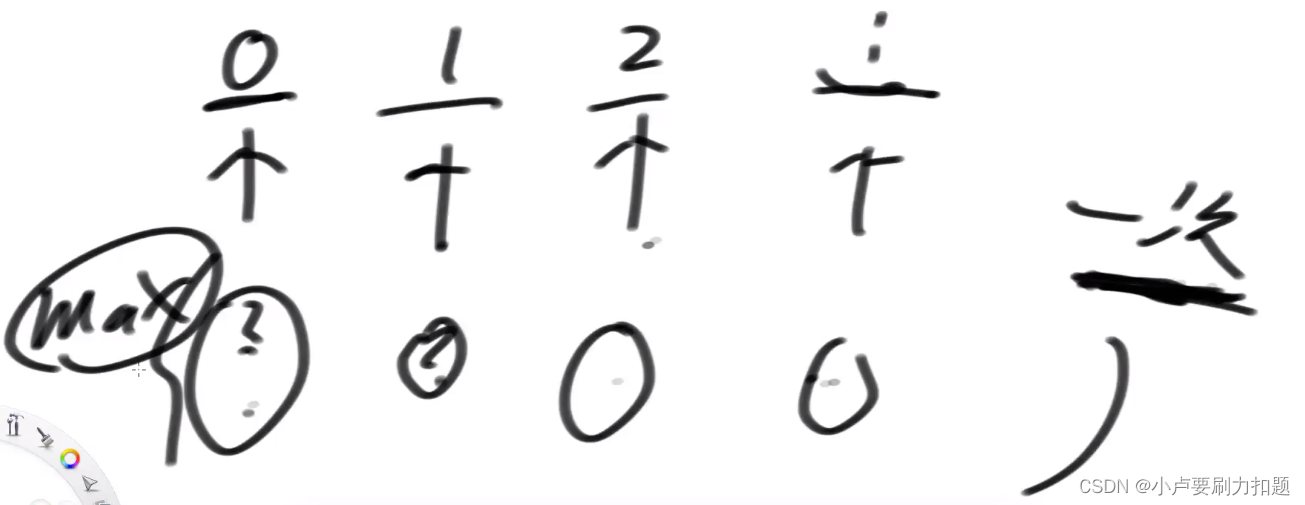
只能做一次交易,
0时刻是这一次交易的卖出时机,我能挣多少钱
1时刻是这一次交易的卖出时机,我能挣多少钱
2时刻是这一次交易的卖出时机, 我能挣多少钱
3时刻是这一次交易的卖出时机,我能挣多少钱
…
求max
就是答案
代码
classSolution{publicintmaxProfit(int[] prices){if(prices==null||prices.length==0){return0;}int min=prices[0];int ans=0;for(int i=1;i<prices.length;i++){
ans=Math.max(ans,prices[i]-min);
min=Math.min(min,prices[i]);}return ans;}}
122. 买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
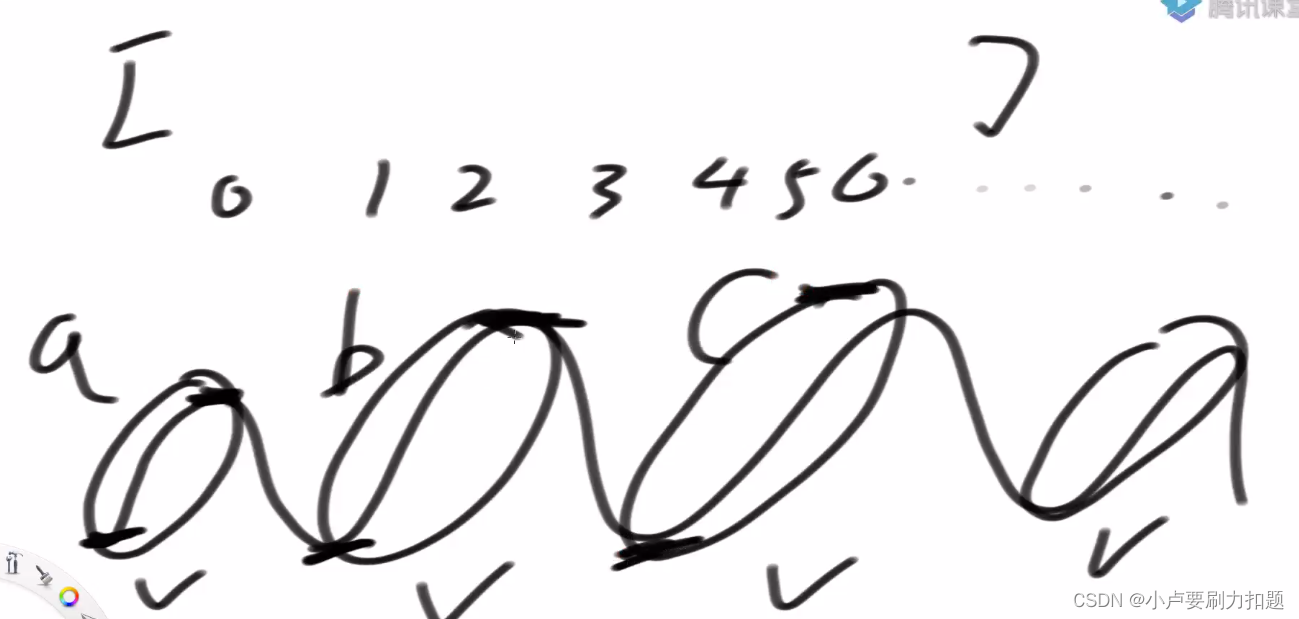
想象整个股市就相当于一个波峰波谷图。 既然他无限制交易,你把每一个爬坡算一个钱, 全累加起来就是答案。
所有爬坡的钱全累加,相当于抓住了每一次行情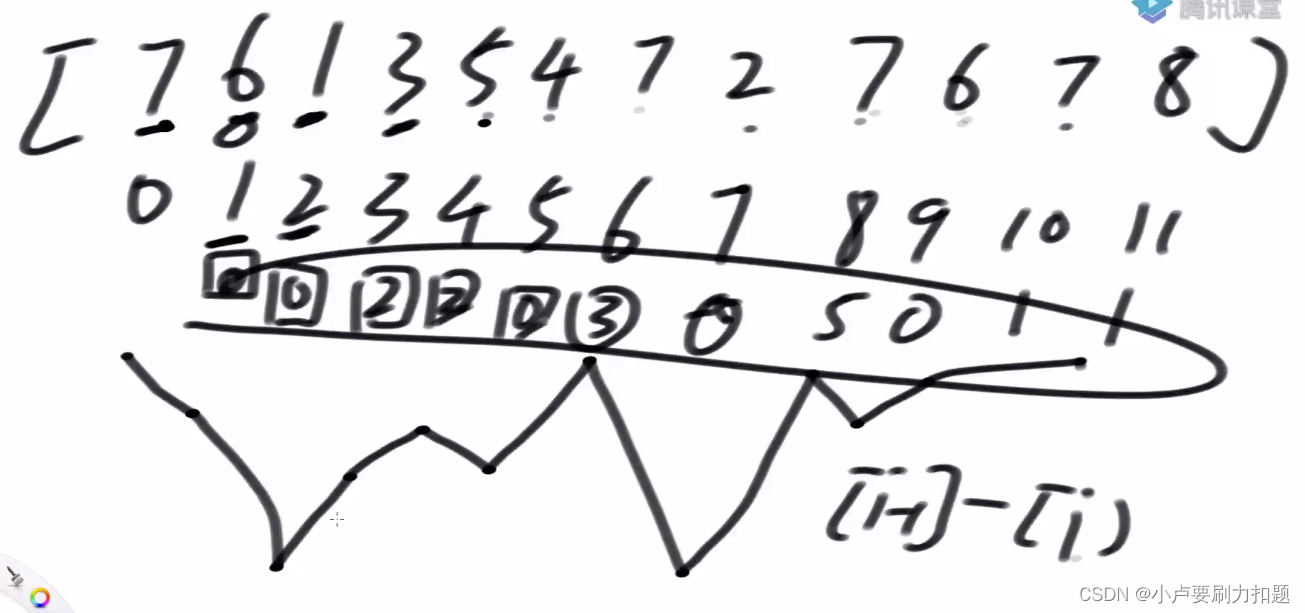
i位置的数减之前的数
小于零认为管案是0
大于零就算入答案里去,把找寻爬坡这个过程变成了相邻两个数相减的过程。
代码
classSolution{publicintmaxProfit(int[] prices){int n=prices.length;if(prices==null||n==0){return0;}int ans=0;for(int i=1;i<n;i++){
ans+=(prices[i]-prices[i-1])>0?prices[i]-prices[i-1]:0;}return ans;}}
188. 买卖股票的最佳时机 IV
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
如果最多的交易次数K>=N/2,等同于交易次数不限,等同于股票问题2
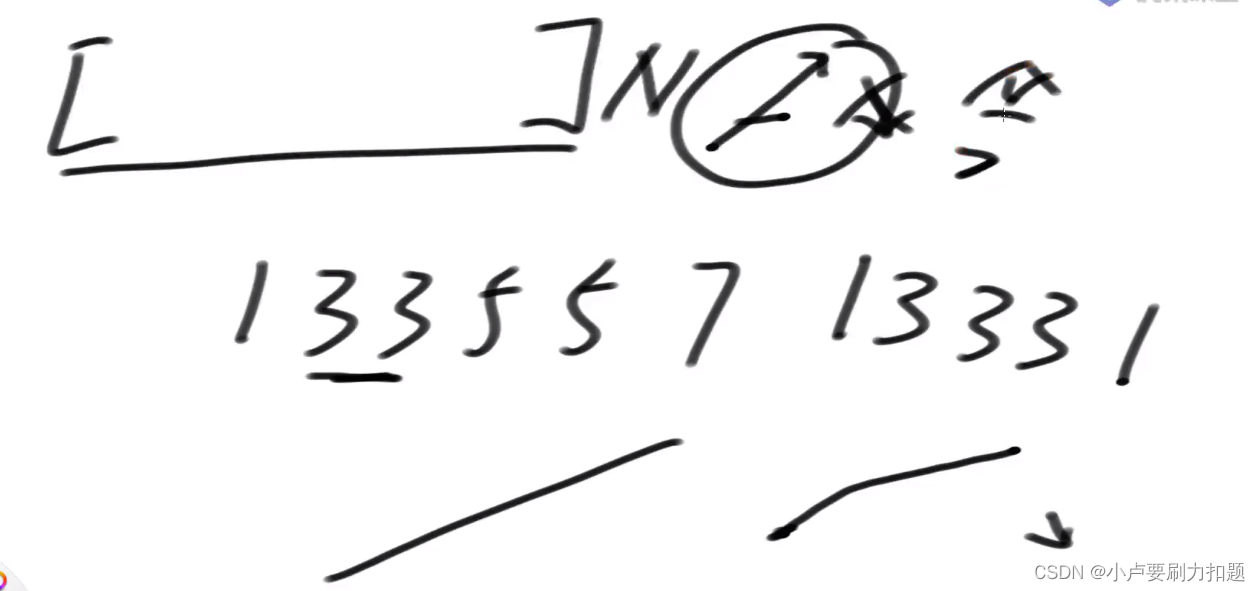
一个长度为N的数组中,爬坡最多N/2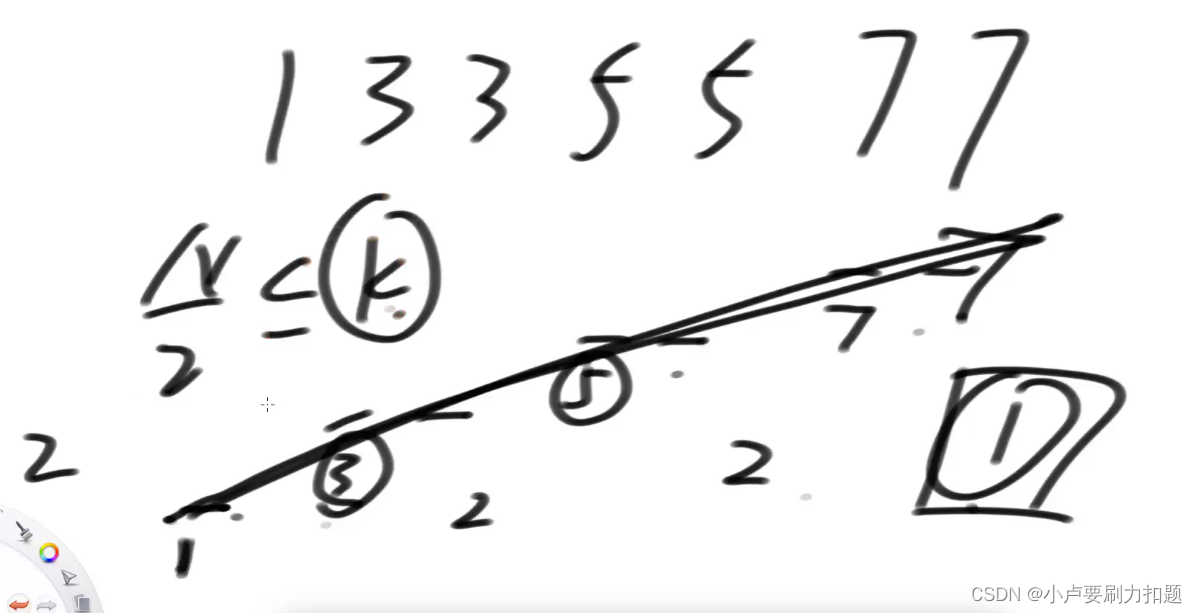
一直爬坡:多次交易跟一次交易效果一样
如果没有超过N/2
从左往右+业务限制
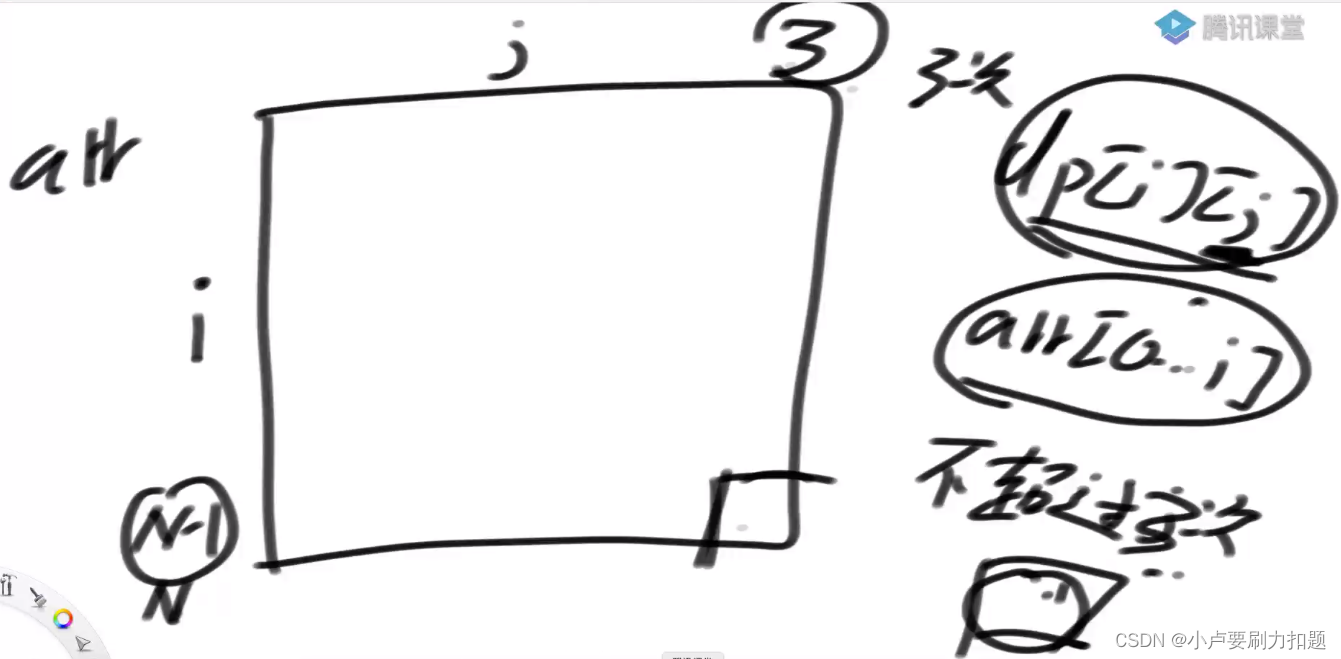
dp[i][j]:只能在arr 0…i上做交易,而且交易次数不要超过j次获得的最大收益
最右下角是答案
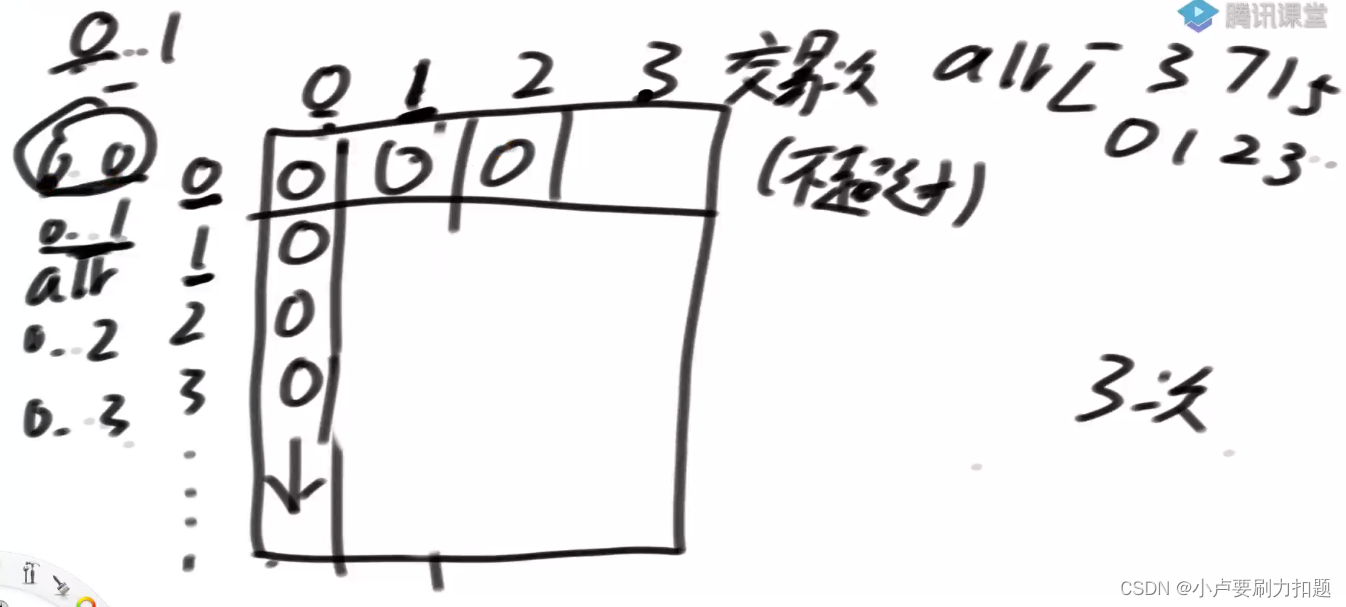
0行, 0列都填0
0行代表0个股票,做j笔交易
0列代表0笔交易
普遍位置dp[8][3]
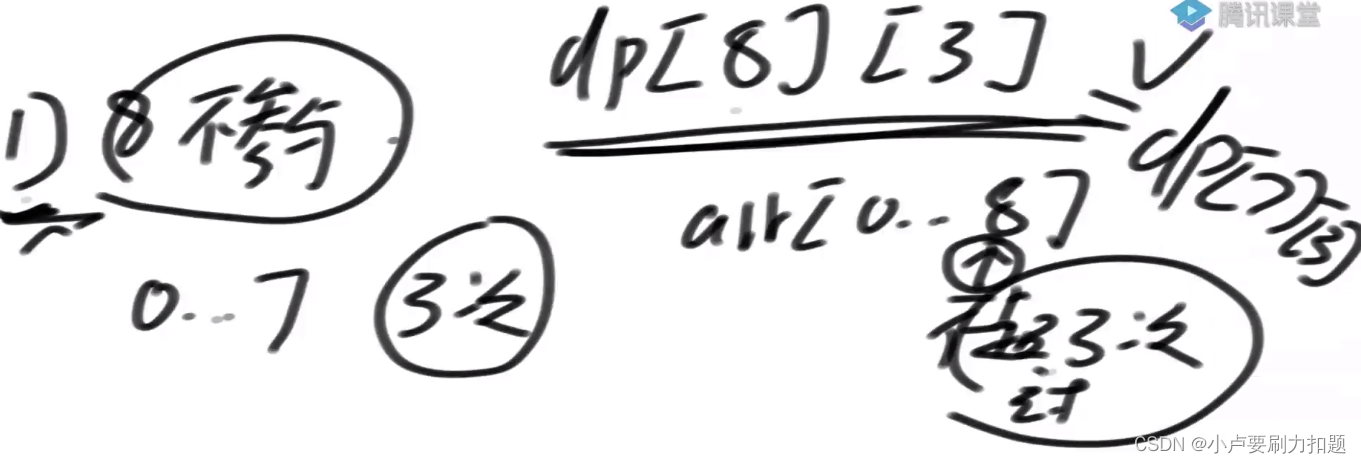
可能性划分,8位置要不要参与交易
1)8位置不参与:dp[7][3]
2)8位置要参与交易,只能是最后一次交易的卖出时机
8位置参与,最后一次交易是啥?
最后一次交易买入时机的可能性: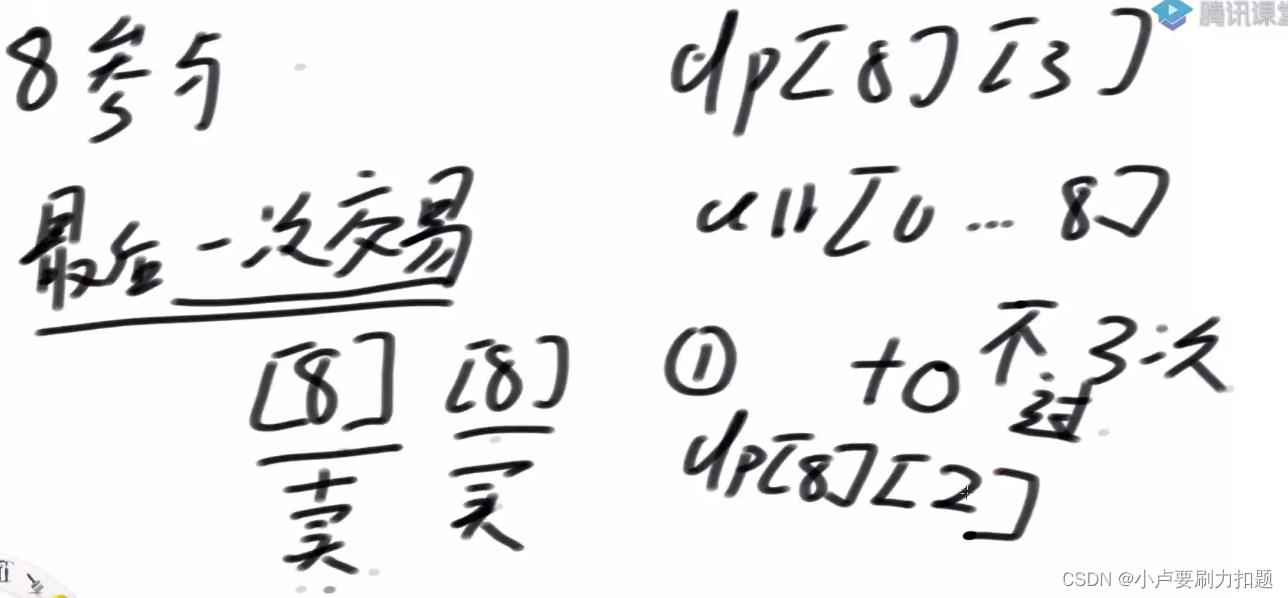
1)8位置买入
2)7位置买入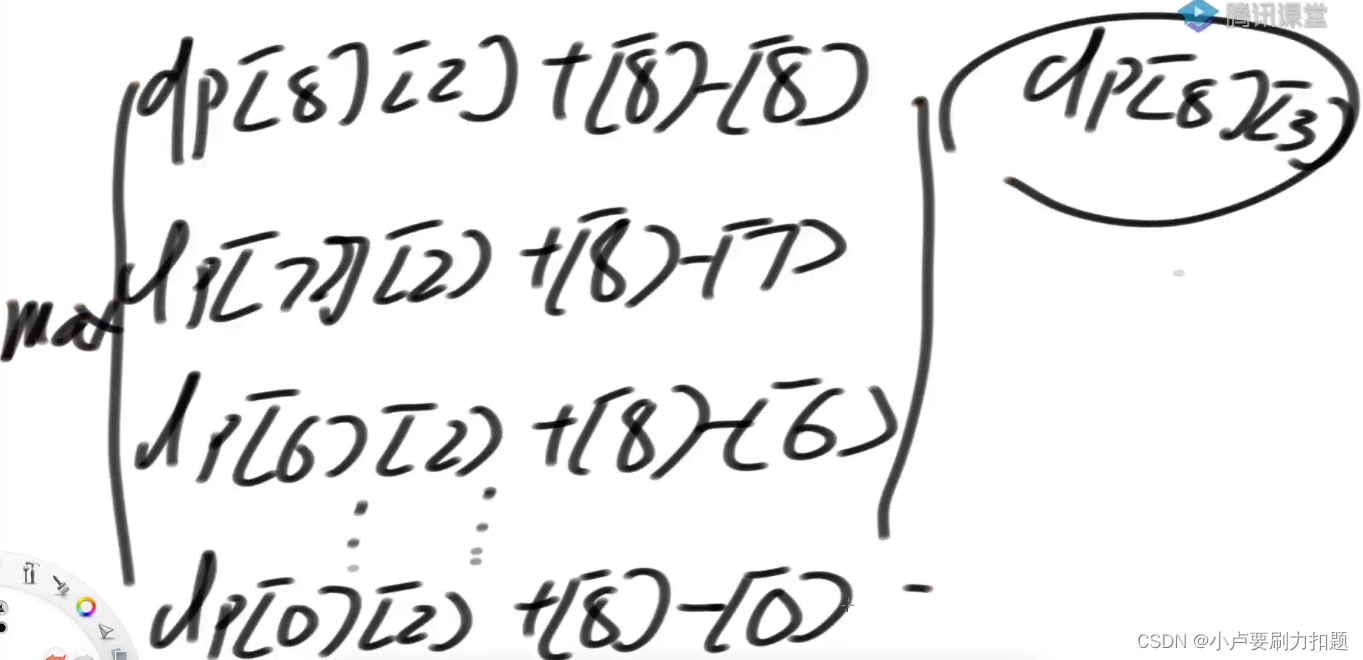
所有的可能性
0到8,交易2次
斜率优化
dp[5][2]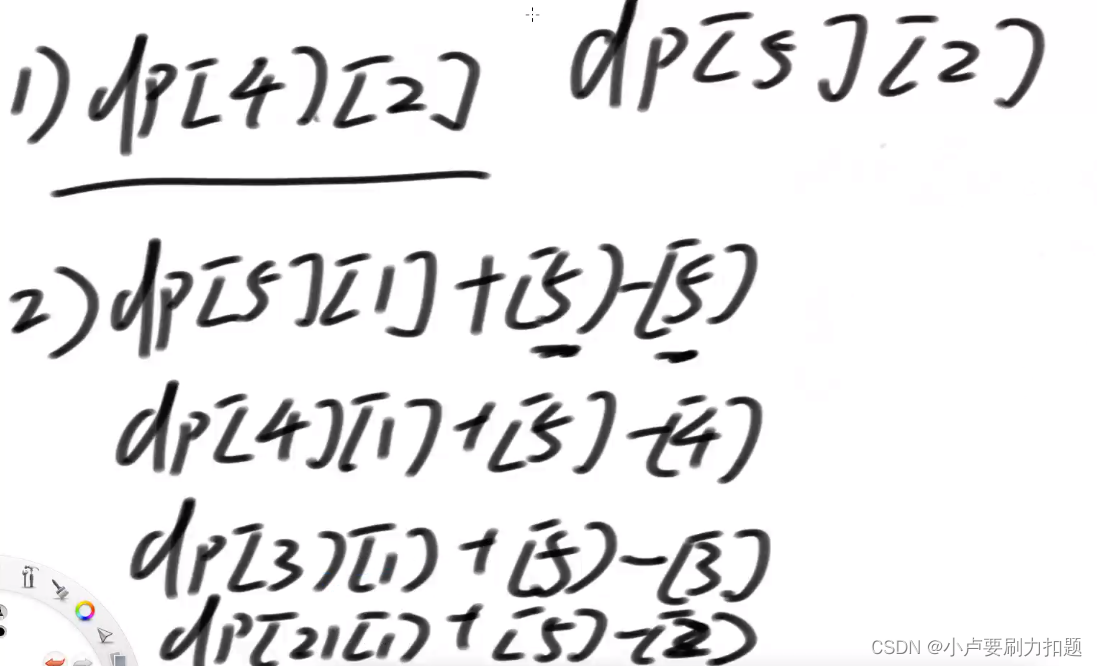
dp[6][2]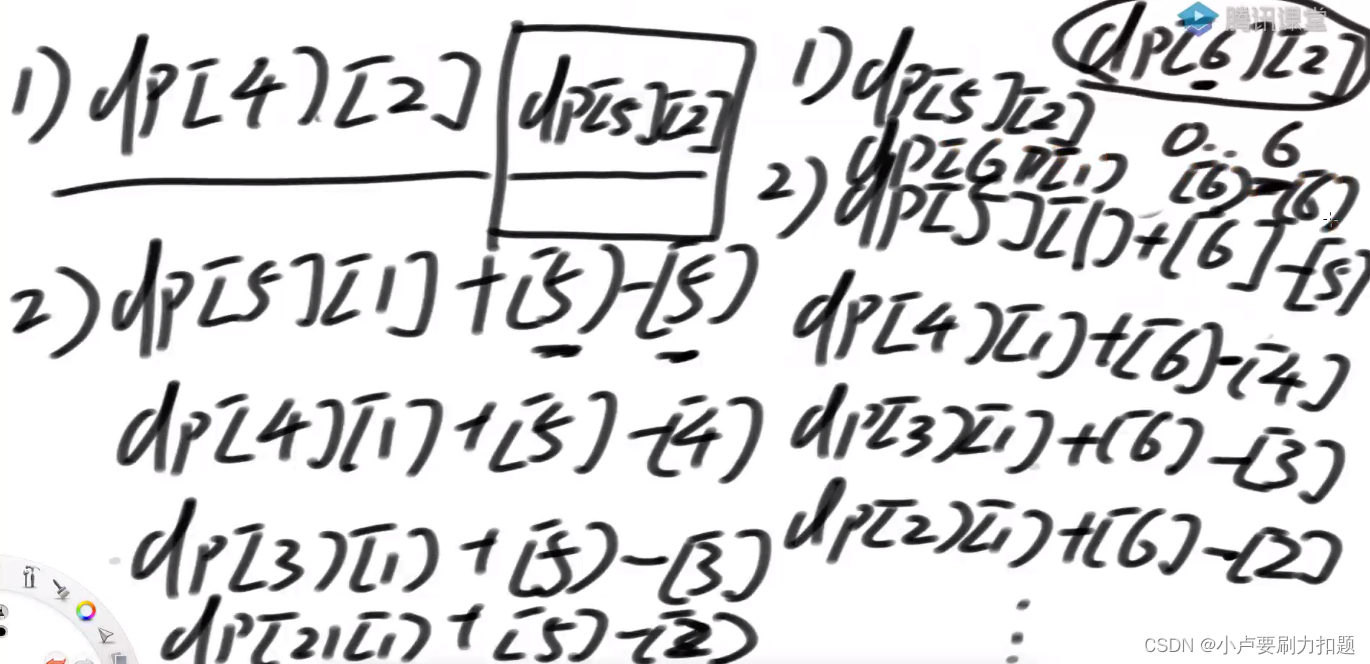
在dp[5][2]中
把枚举的数变成


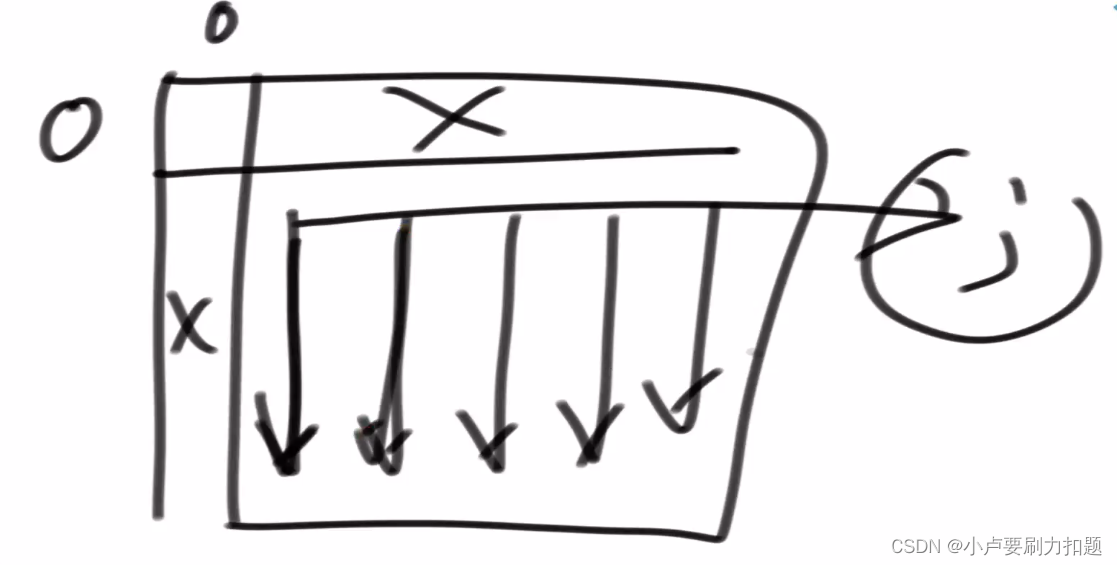
从左到右,从上到下填表
代码
classSolution{publicstaticintallTrans(int[] prices){int ans =0;for(int i =1; i < prices.length; i++){
ans +=Math.max(prices[i]- prices[i -1],0);}return ans;}publicintmaxProfit(int k,int[] prices){int n=prices.length;if(prices==null||n==0){return0;}if(k>=n/2){returnallTrans(prices);}int[][] dp=newint[n][k+1];for(int j=1;j<=k;j++){int p1=dp[0][j];int best=Math.max(dp[1][j-1]-prices[1],dp[0][j-1]-prices[0]);
dp[1][j]=Math.max(p1,best+prices[1]);for(int i=1;i<n;i++){
p1=dp[i-1][j];
best=Math.max(best,dp[i][j-1]-prices[i]);
dp[i][j]=Math.max(p1,best+prices[i]);}}return dp[n-1][k];}}
123. 买卖股票的最佳时机 III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
有了股票问题4,再回头看股票问题3就简单好多了
只是把k变为2而已
代码
classSolution{publicintmaxProfit(int[] prices){if(prices==null||prices.length<2){return0;}int min=prices[0];// 做完一次交易买入第二支股票int onceBuyAndsell=-prices[0];// 做完第一次交易int onceBuyMax=0;int ans=0;for(int i=1;i<prices.length;i++){
ans=Math.max(ans,onceBuyAndsell+prices[i]);
min=Math.min(min,prices[i]);
onceBuyMax=Math.max(onceBuyMax,prices[i]-min);
onceBuyAndsell=Math.max(onceBuyAndsell,onceBuyMax-prices[i]);}return ans;}}
309. 最佳买卖股票时机含冷冻期
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
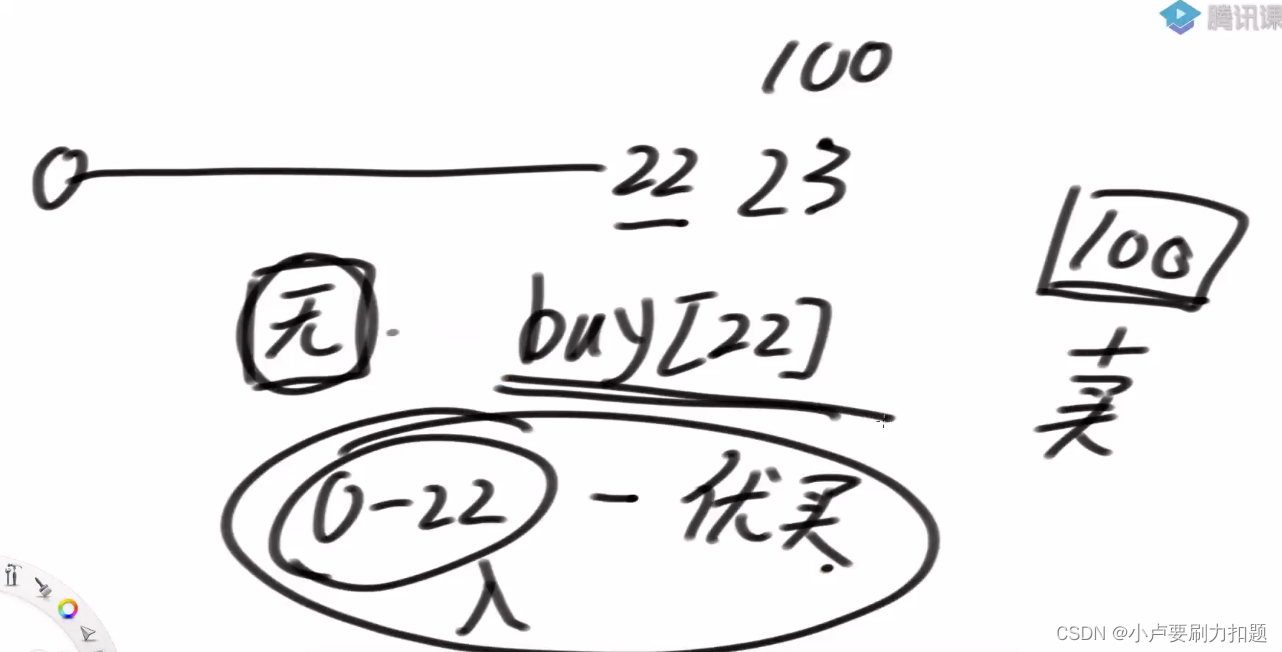
定义新指标buy[22]
022无限次交易获得的收入减去一个比较优良的买入时机,综台起来的最优叫buy[22]23范围上获得无限次交易的最优收益
这个综合起来的最右收益最后再加上100就是0
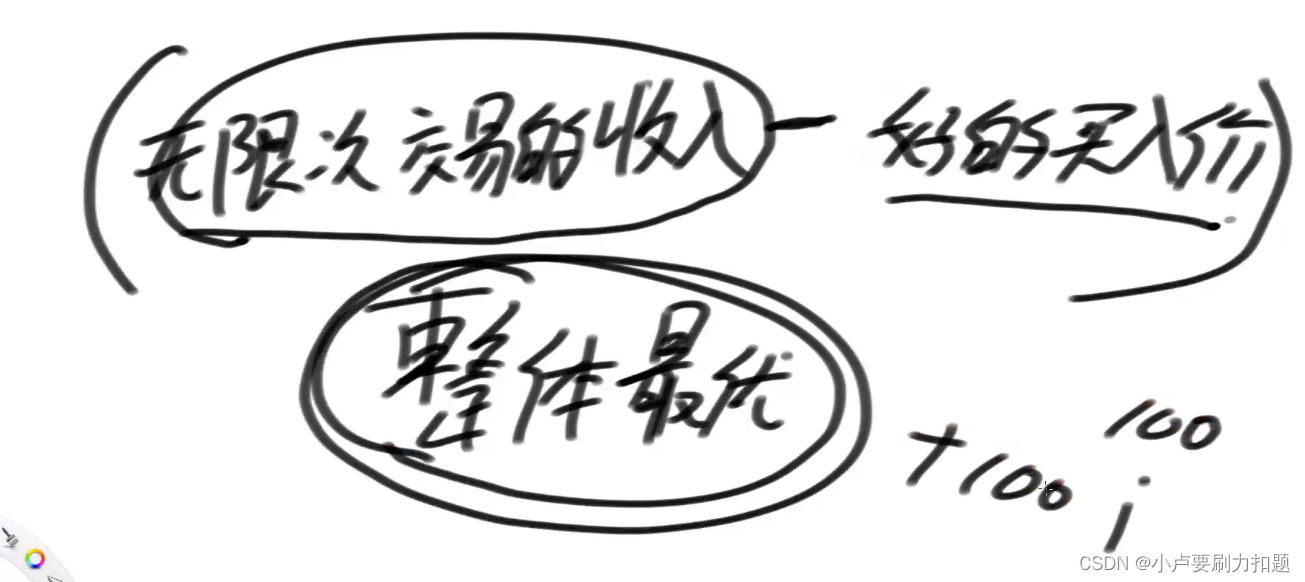
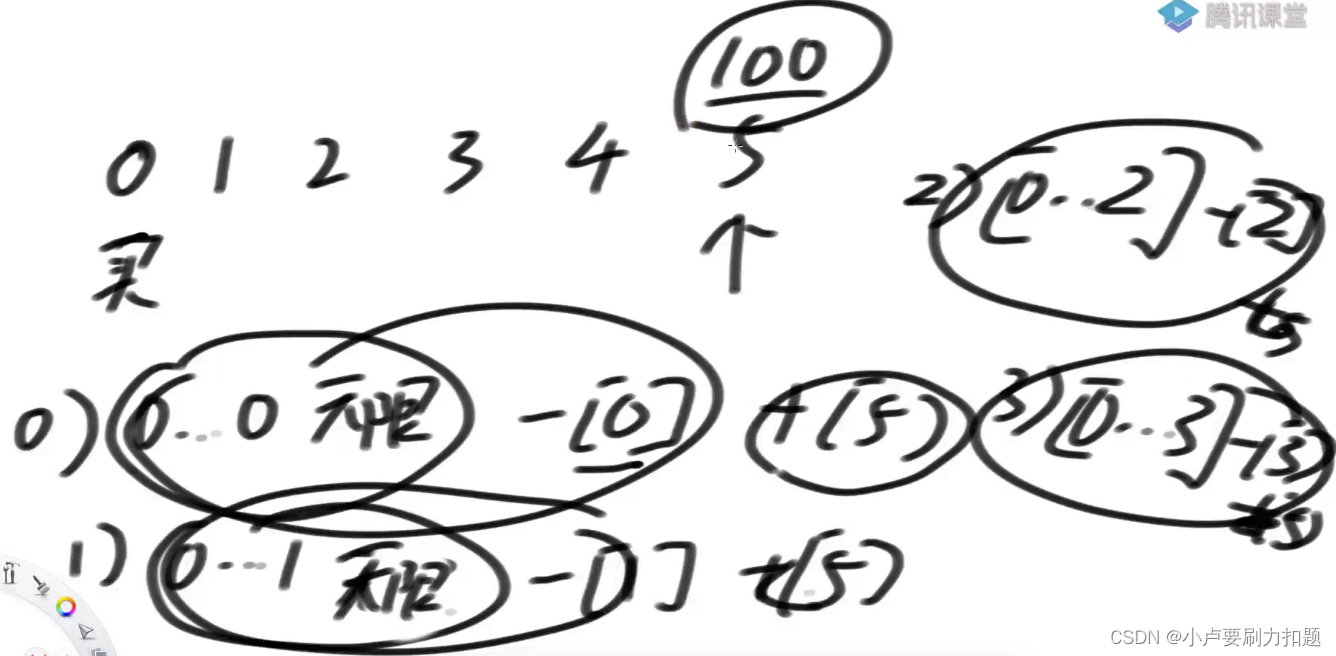
0)最后一次交易必须在0位置买入,00范围上进行无限次交易获得的钱减去0位置的买入价,最后加上5位置的卖出价1范围上进行无限次交易获得的钱减去1位置的买入价最后加上5位置的卖出价
1)最后一次交易必须在1位置买入,0
2)最后一次交易必须在2位置买入,02范围上进行无限次交易获得的钱减去2位置的买入价,最后加上5位置的卖出价3范围上进行无限次交易获得的钱减去3位置的买入价,最后加上5位置的卖出价
3)最后一次交易必须在3位置买入, 0
整体最优就是不加5位置的之前的部分,所有都考虑哪个最优
最后一次操作一定是买动作
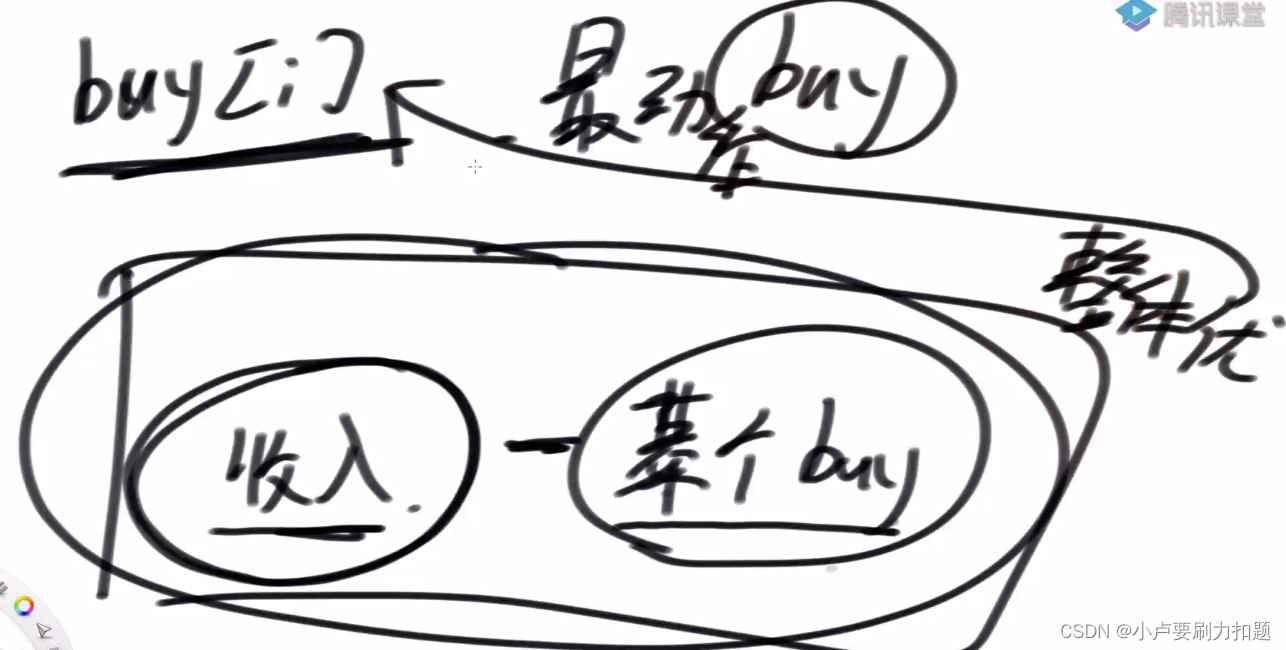
buy[i]:
指的是在0到i的范围上,最后一次操作一定是买的动作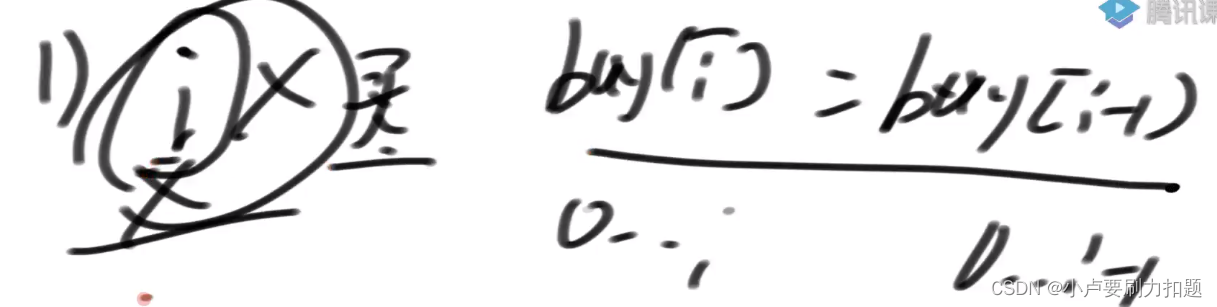
1)不参与,不在i位置买入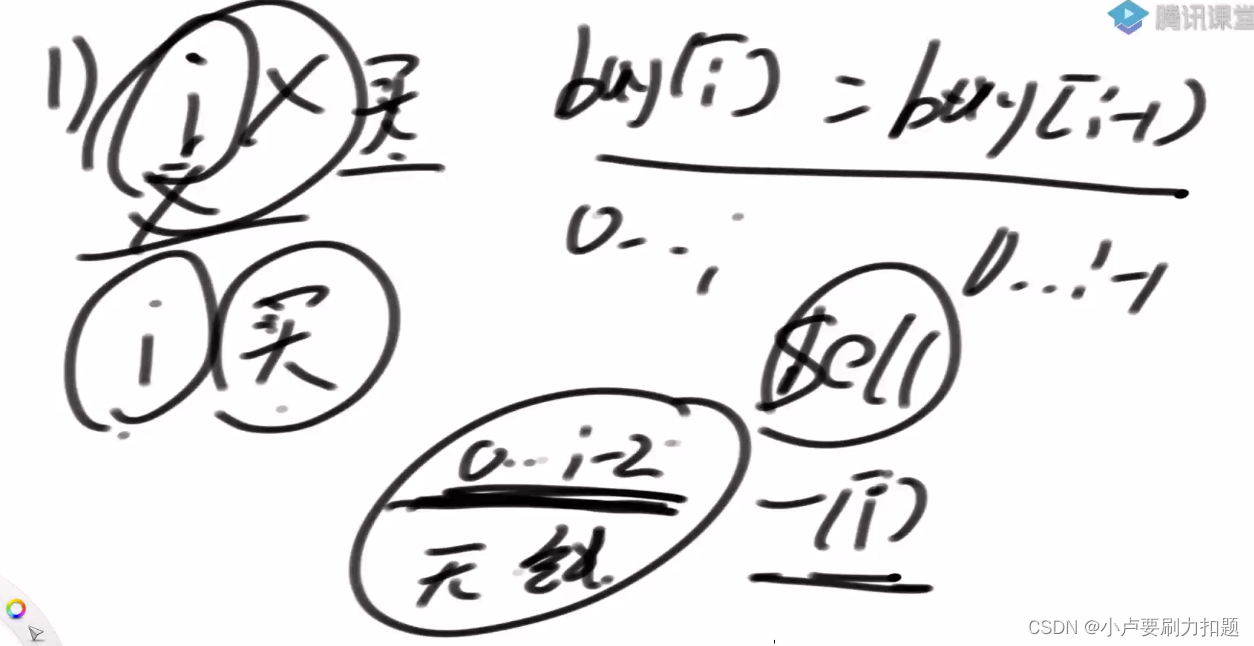
2) i参与,因为cooldown,所以之前是0~i-2范围上无限次交易获得的钱
sell[i]
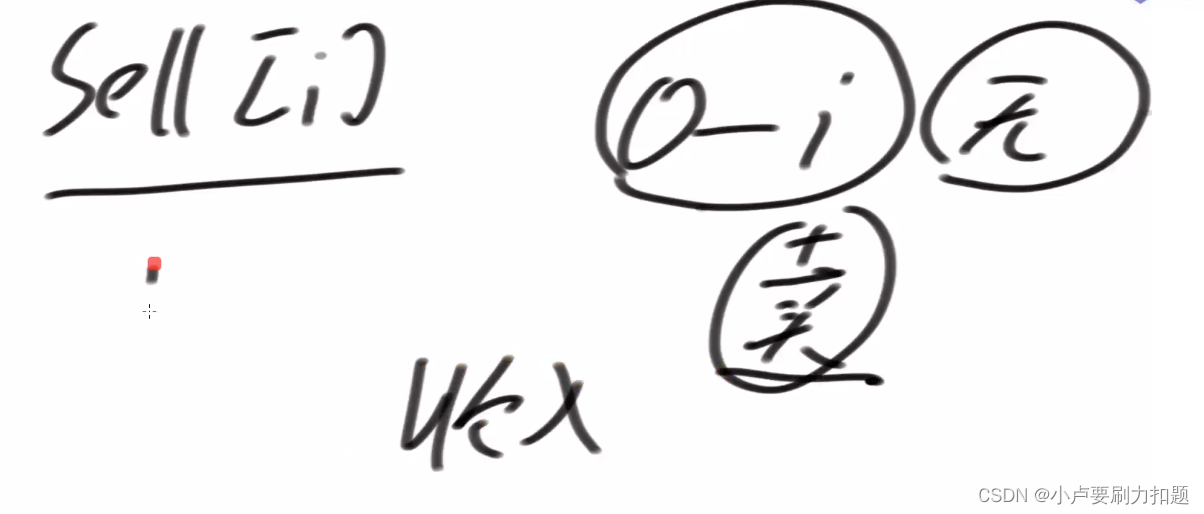
0i做无限次交易,最后一个动作必须是卖,获得的最好收入i-1范围上考虑综合的无限次收入,以及一个最优的买入价,再加上你此时i位置的值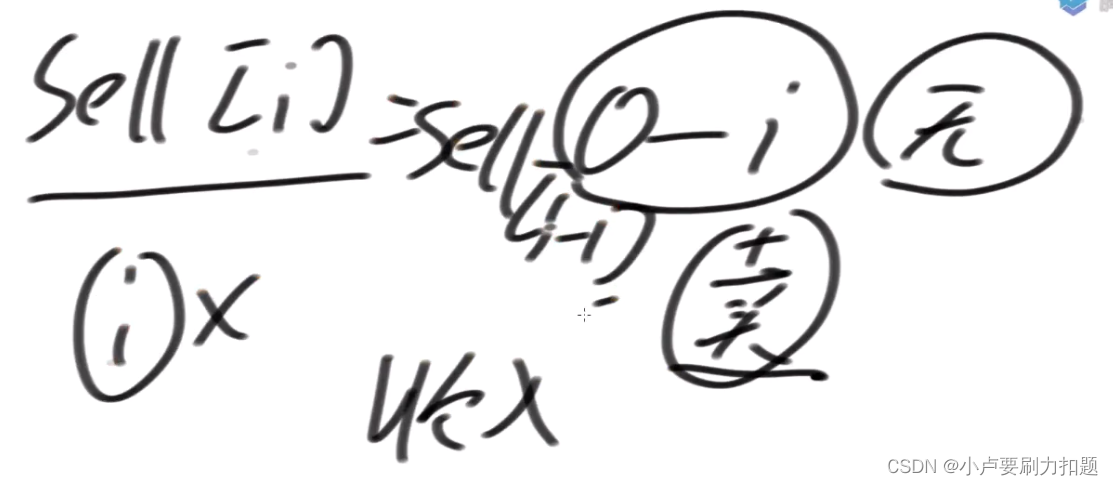
1)不参与, sell[i]= sell[i-1]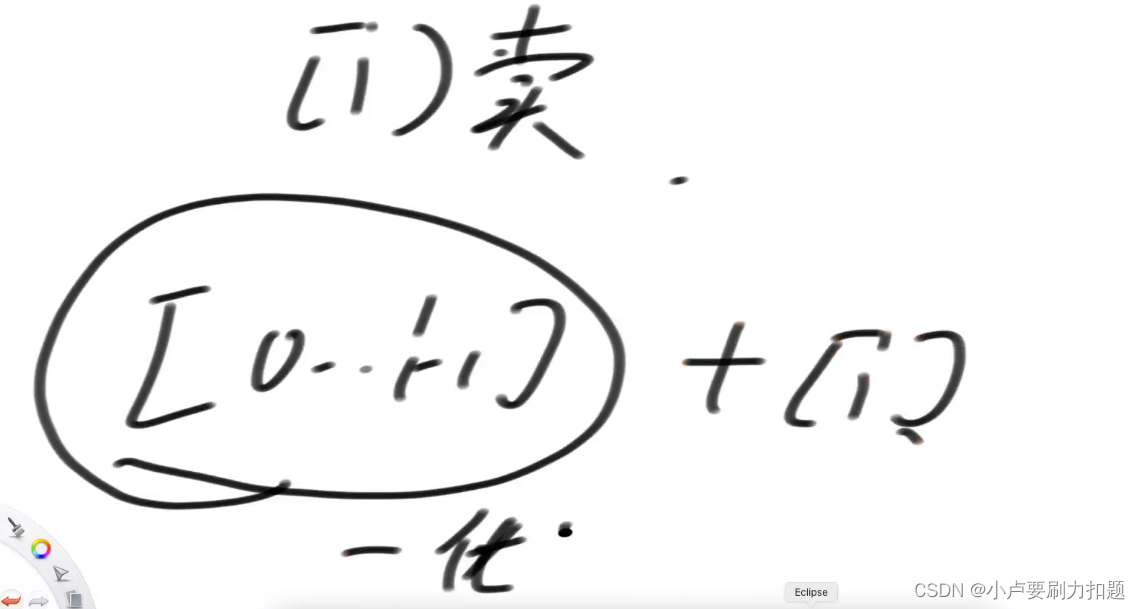
2) i参与,
i是最后的卖出时刻
就是0
代码
publicstaticintmaxProfit(int[] prices){if(prices.length <2){return0;}intN= prices.length;int[] buy =newint[N];int[] sell =newint[N];// buy[0] 不需要设置 buy[0] = -arr[0]// sell[0] = 0
buy[1]=Math.max(-prices[0],-prices[1]);
sell[1]=Math.max(0, prices[1]- prices[0]);for(int i =2; i <N; i++){
buy[i]=Math.max(buy[i -1], sell[i -2]- prices[i]);
sell[i]=Math.max(sell[i -1], buy[i -1]+ prices[i]);}return sell[N-1];}
空间压缩
publicstaticintmaxProfit(int[] prices){if(prices.length <2){return0;}int buy1 =Math.max(-prices[0],-prices[1]);int sell1 =Math.max(0, prices[1]- prices[0]);int sell2 =0;for(int i =2; i < prices.length; i++){int tmp = sell1;
sell1 =Math.max(sell1, buy1 + prices[i]);
buy1 =Math.max(buy1, sell2 - prices[i]);
sell2 = tmp;}return sell1;}
714. 买卖股票的最佳时机含手续费
给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
与上一题相似
buy:0到i最好的买入时机
sell:0到i最好的卖出时机
代码
publicstaticintmaxProfit(int[] arr,int fee){if(arr ==null|| arr.length <2){return0;}intN= arr.length;// 0..0 0 -[0] - feeint bestbuy =-arr[0]- fee;// 0..0 卖 0int bestsell =0;for(int i =1; i <N; i++){// 来到i位置了!// 如果在i必须买 收入 - 批发价 - feeint curbuy = bestsell - arr[i]- fee;// 如果在i必须卖 整体最优(收入 - 良好批发价 - fee)int cursell = bestbuy + arr[i];
bestbuy =Math.max(bestbuy, curbuy);
bestsell =Math.max(bestsell, cursell);}return bestsell;}
版权归原作者 小卢要刷力扣题 所有, 如有侵权,请联系我们删除。