就前不久完成的RSA加解密实现这一实验来水一篇文章
算法原理:
一.米勒拉宾素性检测算法
米勒-拉宾(MillerRabbin)素性测试算法是一个高效判断素数的方法。
其涉及到的原理如下:
1、费马小定理:如果p为质数 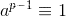 (在mod p 的情况下)
2、对于任意一个小于p的正整数x,发现1(模p)的非平凡平方根存在,则说明p是合数。
其中定理第二部分可以理解为:
如果p是一个素数,0 < x< p, 则方程  ≡ 1(mod p) 的解为 x=1 ,x= p-1
≡ 1(mod p) 的解为 x=1 ,x= p-1
反之如果 x^ 2 ≡ 1(mod p) 的解不是 x=1 ,x= p-1 那 p 就不是素数
二.拓展欧几里得算法
如果a、b是整数,那么一定存在整数x、y使得ax+by=gcd(a,b)
1、首先,对于要求最大公约数的两个数 a, b 一定存在满足上式关系;
2、对上式往下层层递推:
(1)…ax + by = gcd (a, b);
(2)…bx1 + a % by1 = gcd (b, a%b); (运用欧几里算法)
(3)…gcd (a, b) = gcd(b,a%b); (欧几里得算法)
(4)…ax + by = b x1 + a % b*y1; (在计算机里 a % b = (a - a / b * b))
(5)…ax + by = bx1 + ay1 - a / b * by1;
(6)…ax + by = ay1 + b (x1 - a / b) y1; (合并同类项)
(7)…x = y1, y = x1 - a / b * y1; (结论)
由此得出结论,每一层的 x 都等于下一层的 y,每一层的 y 都等于下一层的 x1 - a / b * y1;
三.模平方重复算法
模平方重复算法可用于快速幂的实现,是RSA加解密的重要组成部件。具体见下图,大致思路为将指数转化为2进制形式,然后循环相乘并取模。

四.RSA加解密原理
RSA算法主要包括:密钥生成,加密过程和解密过程。
(1)加密过程。在密钥生成过程中,首先生成两个大的质数(素数)p和q,令n=pq ;m=(p-1)(q-1),选取较小的数e,使e 和m互质,即e和m的最大公约数为1,然后生成d,使d*e(mod m)=1,最后丢弃P,q,m,则加密密钥为e, n,解密密钥为d和n.
(2) 加密过程。将明文x加密成密文y的计算公式为:y=x^e (mod n)。从公式可见,加密牵涉到明文和加密密钥。因此,密文即使被截获,也无法被解读。
(3) 解密过程。将密文y解密成明文x的计算公式为:x=y^d (mod n)。从公式可见,解密至牵涉到解密密钥和密文。
- 算法设计
快速幂算法
利用模平方重复思想,快速进行幂指数运算
int pow_mod(int a,int b,int c){
int res=1;
while(b){
if((b&1)==1)res=(res*a)%c;
a=(a*a)%c;
b>>=1;
}
return (res+c)%c;
}
随机大素数(p,q)生成算法
将系统时间作为种子,产生随机数,并利用米勒拉宾算法进行检测,生成两个不相等的大素数。
//米勒拉宾素性检测
bool Miller_Rabbin(int a,int n){
//把n-1 转化成 (2^r)*d
int s=n-1,r=0;
while((s&1)==0){
s>>=1;r++;
}
//算出 2^d 存在 k 里
int k=pow_mod(a,s,n);
//二次探测 看变化过程中是不是等于1 或 n-1
if(k==1)return true;
for(int i=0;i<r;i++,k=k*k%n){
if(k==n-1)return true;
}
return false;
}
//素性判定
bool isprime(int n){
int times=7;
int prime[100]={2,3,5,7,11,233,331};
for(int i=0;i<times;i++){
if(n==prime[i])return true;
if(Miller_Rabbin(prime[i],n)==false)return false;//未通过探测 返回假
}
return true;//所有探测结束 返回真
}
//利用米勒拉宾素性检测产生随机素数(100以内)
int produceRandom(){
time_t t;
int randnum;
do{
srand((unsigned)time(&t));
randnum = (rand())%100;
if(isprime(randnum))return randnum;
}while(1);
}
扩展欧几里得求逆元
根据扩展欧几里得算法求得e相对于F_n的逆元d
//拓展欧几里得算法求逆元
int exgcd(int a,int b,int &x,int &y)
{
int t,gcd;
if(b==0)
{
x=1,y=0;
return a;
}
gcd=exgcd(b,a%b,x,y);
t=x,x=y,y=t-a/b*y;
return gcd;
}
- 运行结果
对“明文.txt”进行加密得到“密文.txt”
对“密文.txt”进行解密得到“解密文.txt”
由此可见,英文大小写均可实现随机密钥的加解密


源码如下:
#include<cstdio>
#include<fstream>
#include<string.h>
#include<iostream>
#include<algorithm>
#include<ctime>
using namespace std;
typedef long long ll;
int p = 0;
int q = 0;
int len = 0;
//拓展欧几里得算法求逆元
int exgcd(int a,int b,int &x,int &y)
{
int t,gcd;
if(b==0)
{
x=1,y=0;
return a;
}
gcd=exgcd(b,a%b,x,y);
t=x,x=y,y=t-a/b*y;
return gcd;
}
//快速幂(模平方重复)
int pow_mod(int a,int b,int c){
int res=1;
while(b){
if((b&1)==1)res=(res*a)%c;
a=(a*a)%c;
b>>=1;
}
return (res+c)%c;
}
//米勒拉宾素性检测
bool Miller_Rabbin(int a,int n){
//把n-1 转化成 (2^r)*d
int s=n-1,r=0;
while((s&1)==0){
s>>=1;r++;
}
//算出 2^d 存在 k 里
int k=pow_mod(a,s,n);
if(k==1)return true;
for(int i=0;i<r;i++,k=k*k%n){
if(k==n-1)return true;
}
return false;
}
bool isprime(int n){
int times=7;
int prime[100]={2,3,5,7,11,233,331};
for(int i=0;i<times;i++){
if(n==prime[i])return true;
if(Miller_Rabbin(prime[i],n)==false)return false;//未通过探测 返回假
}
return true;//所有探测结束 返回真
}
//利用米勒拉宾素性检测产生随机素数(100以内)
int produceRandom(){
int randnum;
do{
randnum = (rand())%100;
if(isprime(randnum))return randnum;
}while(1);
}
int main(){
srand(time(NULL));
int i;
here:
p = produceRandom();
q = produceRandom();
while(q==p)q=produceRandom();//p和q不能相等
int n = p*q;
while(n<128)goto here; //确保n足够大,因为char为八位即-128~127,所以n至少要大于127
int F_n = (p-1)*(q-1);
int x,y;
int e = 7;
exgcd(e,F_n,x,y);
int d = (x + F_n) % F_n;
int flag;
while(1){
char text[1000]="";
cout<<"请选择功能:\n 1.加密文件\n 2.解密文件\n 0.退出"<<endl;
cin>>flag;
if (!flag) break;
else if ((flag != 1) && (flag != 2))
{
cout << "输入不合法,请重新输入!" << endl << endl;
continue;
}
switch (flag)
{
case 1:{
char ch;
cout<<"加密密钥为:("<<e<<','<<n<<')'<<endl;
ofstream ofs;
ifstream ifs;
ofs.open("密文.txt",ios::trunc|ios::out);
ifs.open("明文.txt",ios::in);
i = 0;
while(ifs>>ch){
text[i++]=ch;
}
len = strlen(text);
int ming [strlen(text)];
for(i = 0;i<strlen(text);i++){
ming[i]=text[i];
ming[i]=pow_mod(ming[i],e,n);
ofs<<ming[i]<<' ';
}
ofs.close();
ifs.close();
break;}
case 2:{
char ch;
int c[len];
cout<<"解密密钥为:("<<d<<','<<n<<')'<<endl;
ofstream ofs;
ifstream ifs;
ofs.open("解密文.txt",ios::trunc|ios::out);
ifs.open("密文.txt",ios::in);
for(i = 0;i<len;i++){
ifs>>c[i];
ch = pow_mod(c[i],d,n);
ofs<<ch;
}
ofs.close();
ifs.close();
break;}
}
}
return 0;
}
参考文章:
米勒-拉宾素性检验(MillerRabbin)算法详解_1900_的博客-CSDN博客_米勒拉宾素性检验
版权归原作者 陆仁伽 所有, 如有侵权,请联系我们删除。